篇一 :高中数学导数知识点归纳总结
核心出品
必属精品
免费下载
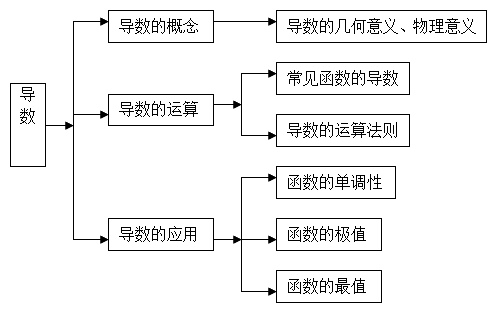
导数
考试内容:
导数的背影.导数的概念.多项式函数的导数.利用导数研究函数的单调性和极值.函数的最大值和最小值.
考试要求:(1)了解导数概念的某些实际背景.(2)理解导数的几何意义.(3)掌握函数,y=c(c为常数)、y=xn(n∈N+)的导数公式,会求多项式函数的导数.(4)理解极大值、极小值、最大值、最小值的概念,并会用导数求多项式函数的单调区间、极大值、极小值及闭区间上的最大值和最小值.(5)会利用导数求某些简单实际问题的最大值和最小值.
§14. 导数 知识要点

1. 导数(导函数的简称)的定义:设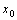 是函数
是函数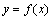 定义域的一点,如果自变量
定义域的一点,如果自变量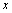 在
在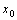 处有增量
处有增量 ,则函数值
,则函数值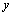 也引起相应的增量
也引起相应的增量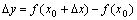 ;比值
;比值 称为函数
称为函数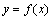 在点
在点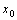 到
到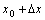 之间的平均变化率;如果极限
之间的平均变化率;如果极限 存在,则称函数
存在,则称函数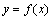 在点
在点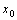 处可导,并把这个极限叫做
处可导,并把这个极限叫做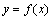 在
在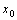 处的导数,记作
处的导数,记作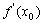 或
或 ,即
,即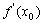 =
= .
.
注:① 是增量,我们也称为“改变量”,因为
是增量,我们也称为“改变量”,因为 可正,可负,但不为零.
可正,可负,但不为零.
②以知函数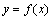 定义域为
定义域为 ,
,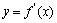 的定义域为
的定义域为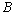 ,则
,则 与
与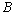 关系为
关系为 .
.
2. 函数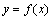 在点
在点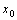 处连续与点
处连续与点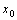 处可导的关系:
处可导的关系:
⑴函数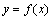 在点
在点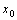 处连续是
处连续是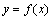 在点
在点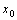 处可导的必要不充分条件.
处可导的必要不充分条件.
可以证明,如果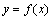 在点
在点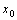 处可导,那么
处可导,那么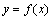 点
点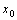 处连续.
处连续.
…… …… 余下全文
篇二 :导数高考知识点总结(最全)
导数知识点归纳及应用
●知识点归纳
一、相关概念
1.导数的概念
函数y=f(x),如果自变量x在x 处有增量
处有增量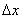 ,那么函数y相应地有增量
,那么函数y相应地有增量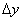 =f(x
=f(x +
+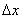 )-f(x
)-f(x ),比值
),比值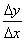 叫做函数y=f(x)在x
叫做函数y=f(x)在x 到x
到x +
+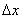 之间的平均变化率,即
之间的平均变化率,即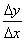 =
= 。如果当
。如果当 时,
时,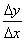 有极限,我们就说函数y=f(x)在点x
有极限,我们就说函数y=f(x)在点x 处可导,并把这个极限叫做f(x)在点x
处可导,并把这个极限叫做f(x)在点x 处的导数,记作f’(x
处的导数,记作f’(x )或y’|
)或y’|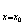 。即f(x
。即f(x )=
)=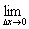
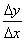 =
=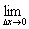
 。
。
说明:
(1)函数f(x)在点x 处可导,是指
处可导,是指 时,
时,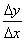 有极限。如果
有极限。如果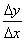 不存在极限,就说函数在点x
不存在极限,就说函数在点x 处不可导,或说无导数。
处不可导,或说无导数。
(2)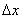 是自变量x在x
是自变量x在x 处的改变量,
处的改变量,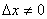 时,而
时,而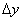 是函数值的改变量,可以是零。
是函数值的改变量,可以是零。
由导数的定义可知,求函数y=f(x)在点x 处的导数的步骤:
处的导数的步骤:
① 求函数的增量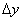 =f(x
=f(x +
+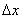 )-f(x
)-f(x );
);
② 求平均变化率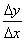 =
= ;
;
③ 取极限,得导数f’(x )=
)=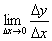 。
。
例:设f(x)= x|x|, 则f′( 0)= .
[解析]:∵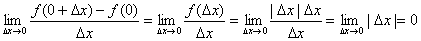
∴f′( 0)=0
2.导数的几何意义
函数y=f(x)在点x 处的导数的几何意义是曲线y=f(x)在点p(x
处的导数的几何意义是曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率。也就是说,曲线y=f(x)在点p(x
))处的切线的斜率。也就是说,曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率是f’(x
))处的切线的斜率是f’(x )。相应地,切线方程为y-y
)。相应地,切线方程为y-y =f/(x
=f/(x )(x-x
)(x-x )。
)。
…… …… 余下全文
篇三 :导数知识点总结
导数 知识要点
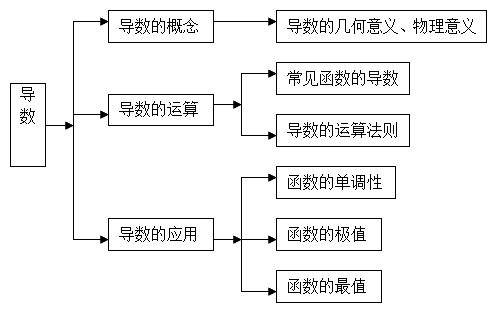
1. 导数(导函数的简称)的定义:设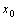 是函数
是函数 定义域的一点,如果自变量
定义域的一点,如果自变量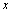 在
在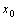 处有增量
处有增量 ,则函数值
,则函数值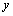 也引起相应的增量
也引起相应的增量 ;比值
;比值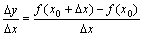 称为函数
称为函数 在点
在点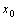 到
到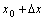 之间的平均变化率;如果极限
之间的平均变化率;如果极限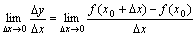 存在,则称函数
存在,则称函数 在点
在点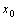 处可导,并把这个极限叫做
处可导,并把这个极限叫做 在
在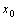 处的导数,记作
处的导数,记作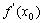 或
或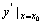 ,即
,即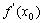 =
=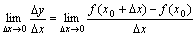 .
.
注:① 是增量,我们也称为“改变量”,因为
是增量,我们也称为“改变量”,因为 可正,可负,但不为零.
可正,可负,但不为零.
②已知函数 定义域为
定义域为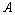 ,
, 的定义域为
的定义域为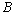 ,则
,则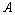 与
与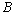 关系为
关系为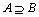 .
.
2. 函数 在点
在点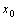 处连续与点
处连续与点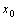 处可导的关系:
处可导的关系:
⑴函数 在点
在点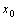 处连续是
处连续是 在点
在点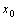 处可导的必要不充分条件.
处可导的必要不充分条件.
可以证明,如果 在点
在点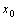 处可导,那么
处可导,那么 点
点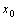 处连续.
处连续.
事实上,令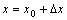 ,则
,则 相当于
相当于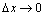 .
.
于是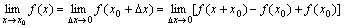
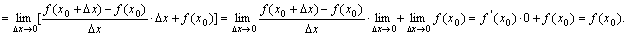 ⑵如果
⑵如果 点
点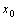 处连续,那么
处连续,那么 在点
在点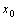 处可导,是不成立的.
处可导,是不成立的.
例: 在点
在点 处连续,但在点
处连续,但在点 处不可导,因为
处不可导,因为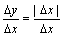 ,当
,当 >0时,
>0时,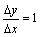 ;当
;当 <0时,
<0时,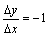 ,故
,故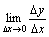 不存在.
不存在.
注:①可导的奇函数函数其导函数为偶函数.
②可导的偶函数函数其导函数为奇函数.
3. 导数的几何意义:
函数 在点
在点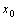 处的导数的几何意义就是曲线
处的导数的几何意义就是曲线 在点
在点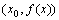 处的切线的斜率,也就是说,曲线
处的切线的斜率,也就是说,曲线 在点P
在点P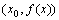 处的切线的斜率是
处的切线的斜率是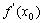 ,切线方程为
,切线方程为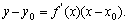
4、几种常见的函数导数:
 (
( 为常数)
为常数) 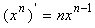 (
(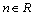 )
)
…… …… 余下全文
篇四 :高中导数及其应用知识点归纳(总结得很好,实用)
第三章 导数及其应用
3.1.2导数的概念(要求熟悉)
1.函数 在
在 处的导数:函数
处的导数:函数 在
在 处的瞬时变化率称为
处的瞬时变化率称为 在
在 处的导数,记作
处的导数,记作 或
或 ,即
,即 。
。
3.1.3导数的几何意义(要求掌握)
1.导数的几何意义:函数 在
在 处的导数就是曲线
处的导数就是曲线 在点
在点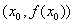 处切线的斜率,
处切线的斜率,
即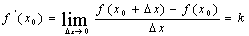 ;
;
2.求切线方程的步骤:(注:已知点 在已知曲线上)
在已知曲线上)
①求导函数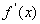 ;②求切线的斜率
;②求切线的斜率 ;③代入直线的点斜式方程:
;③代入直线的点斜式方程: ,并整理。
,并整理。
3.求切点坐标的步骤:①设切点坐标 ;②求导函数
;②求导函数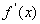 ;③求切线的斜率
;③求切线的斜率 ;④由斜率间的关系列出关于
;④由斜率间的关系列出关于 的方程,解方程求
的方程,解方程求 ;⑤点
;⑤点 在曲线
在曲线 上,将
上,将 代入求
代入求 ,得切点坐标。
,得切点坐标。
3.2导数的计算(要求掌握)
1. 基本初等函数的导数公式:① ;②
;② ;③
;③ ;④
;④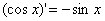 ;
;
⑤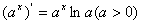 ;⑥
;⑥ ;⑦
;⑦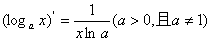 ;⑧
;⑧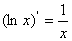 .
.
2.导数运算法则:①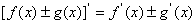 ;②
;②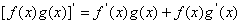 ;
;
③ ;④
;④
3.3.1函数的单调性与导数
(1)在区间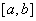 内,
内,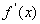 >0,
>0, f(x)为单调递增;
f(x)为单调递增;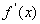 <0,
<0, f(x)为单调递减。
f(x)为单调递减。
(2)用导数求函数单调区间的三个步骤:①确定函数的定义域;②求函数f(x)的导数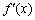 ;③令
;③令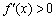 解不等式,得x的范围就是递增区间;④令
解不等式,得x的范围就是递增区间;④令 解不等式,得x的范围就是递减区间。
解不等式,得x的范围就是递减区间。
(3)用导数判断或证明函数的单调性的步骤:①求函数f(x)的导数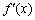 ;②判断
;②判断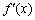 的符号;③给出单调性结论。
的符号;③给出单调性结论。
…… …… 余下全文
篇五 :高中数学导数知识点归纳总结
§14. 导数 知识要点
1. 导数(导函数的简称)的定义:设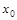 是函数
是函数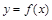 定义域的一点,如果自变量
定义域的一点,如果自变量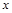 在
在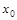 处有增量
处有增量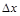 ,则函数值
,则函数值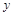 也引起相应的增量
也引起相应的增量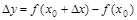 ;比值
;比值 称为函数
称为函数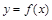 在点
在点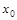 到
到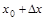 之间的平均变化率;如果极限
之间的平均变化率;如果极限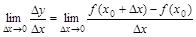 存在,则称函数
存在,则称函数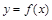 在点
在点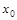 处可导,并把这个极限叫做
处可导,并把这个极限叫做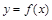 在
在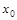 处的导数,记作
处的导数,记作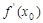 或
或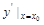 ,即
,即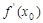 =
=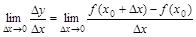 .
.
注:①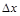 是增量,我们也称为“改变量”,因为
是增量,我们也称为“改变量”,因为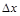 可正,可负,但不为零.
可正,可负,但不为零.
②以知函数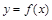 定义域为
定义域为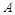 ,
, 的定义域为
的定义域为 ,则
,则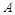 与
与 关系为
关系为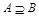 .
.
2. 函数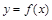 在点
在点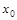 处连续与点
处连续与点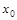 处可导的关系:
处可导的关系:
⑴函数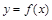 在点
在点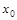 处连续是
处连续是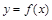 在点
在点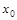 处可导的必要不充分条件.
处可导的必要不充分条件.
可以证明,如果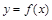 在点
在点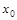 处可导,那么
处可导,那么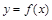 点
点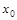 处连续.
处连续.
事实上,令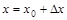 ,则
,则 相当于
相当于 .
.
于是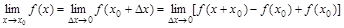
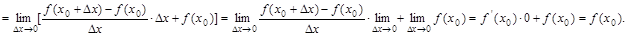 ⑵如果
⑵如果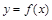 点
点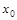 处连续,那么
处连续,那么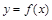 在点
在点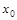 处可导,是不成立的.
处可导,是不成立的.
例: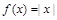 在点
在点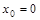 处连续,但在点
处连续,但在点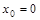 处不可导,因为
处不可导,因为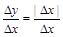 ,当
,当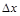 >0时,
>0时,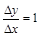 ;当
;当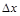 <0时,
<0时,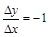 ,故
,故 不存在.
不存在.
注:①可导的奇函数函数其导函数为偶函数.
②可导的偶函数函数其导函数为奇函数.
3. 导数的几何意义:
函数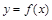 在点
在点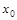 处的导数的几何意义就是曲线
处的导数的几何意义就是曲线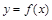 在点
在点 处的切线的斜率,也就是说,曲线
处的切线的斜率,也就是说,曲线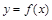 在点P
在点P 处的切线的斜率是
处的切线的斜率是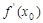 ,切线方程为
,切线方程为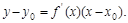
4. 求导数的四则运算法则:
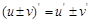
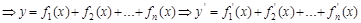
 (
(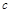 为常数)
为常数)
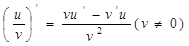
注:①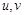 必须是可导函数.
必须是可导函数.
②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.
…… …… 余下全文
篇六 :导数复习知识点总结
高考数学复习详细资料——导数概念与运算知识清单
1.导数的概念
函数y=f(x),如果自变量x在x 处有增量
处有增量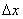 ,那么函数y相应地有增量
,那么函数y相应地有增量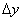 =f(x
=f(x +
+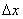 )-f(x
)-f(x ),比值
),比值 叫做函数y=f(x)在x
叫做函数y=f(x)在x 到x
到x +
+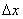 之间的平均变化率,即
之间的平均变化率,即 =
=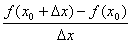 。如果当
。如果当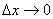 时,
时, 有极限,我们就说函数y=f(x)在点x
有极限,我们就说函数y=f(x)在点x 处可导,并把这个极限叫做f(x)在点x
处可导,并把这个极限叫做f(x)在点x 处的导数,记作f’(x
处的导数,记作f’(x )或y’|
)或y’|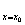 。
。
即f(x )=
)=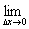
 =
=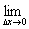
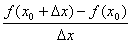 。
。
说明:
(1)函数f(x)在点x 处可导,是指
处可导,是指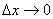 时,
时, 有极限。如果
有极限。如果 不存在极限,就说函数在点x
不存在极限,就说函数在点x 处不可导,或说无导数。
处不可导,或说无导数。
(2)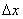 是自变量x在x
是自变量x在x 处的改变量,
处的改变量,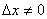 时,而
时,而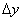 是函数值的改变量,可以是零。
是函数值的改变量,可以是零。
由导数的定义可知,求函数y=f(x)在点x 处的导数的步骤(可由学生来归纳):
处的导数的步骤(可由学生来归纳):
(1)求函数的增量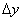 =f(x
=f(x +
+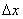 )-f(x
)-f(x );
);
(2)求平均变化率 =
=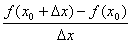 ;
;
(3)取极限,得导数f’(x )=
)= 。
。
2.导数的几何意义
函数y=f(x)在点x 处的导数的几何意义是曲线y=f(x)在点p(x
处的导数的几何意义是曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率。也就是说,曲线y=f(x)在点p(x
))处的切线的斜率。也就是说,曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率是f’(x
))处的切线的斜率是f’(x )。相应地,切线方程为y-y
)。相应地,切线方程为y-y =f/(x
=f/(x )(x-x
)(x-x )。
)。
3.几种常见函数的导数:
…… …… 余下全文
篇七 :高中文科导数知识点汇总
导数公式及知识点
1、函数的单调性
(1)设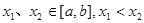 那么
那么
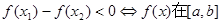 上是增函数;
上是增函数;
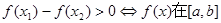 上是减函数.
上是减函数.
(2)设函数 在某个区间内可导,若
在某个区间内可导,若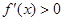 ,则
,则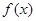 为增函数;若
为增函数;若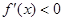 ,则
,则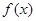 为减函数.
为减函数.
2、函数的奇偶性
对于定义域内任意的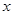 ,都有
,都有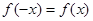 ,则
,则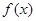 是偶函数;
是偶函数;
对于定义域内任意的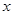 ,都有
,都有 ,则
,则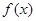 是奇函数。
是奇函数。
奇函数的图象关于原点对称,偶函数的图象关于y轴对称。
3、函数 在点
在点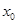 处的导数的几何意义
处的导数的几何意义
函数 在点
在点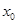 处的导数是曲线
处的导数是曲线 在
在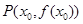 处的切线的斜率
处的切线的斜率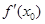 ,相应的切线方程是
,相应的切线方程是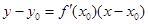 .
.
4、几种常见函数的导数
①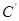
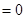 ;②
;②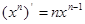 ; ③
; ③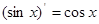 ;④
;④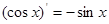 ;
;
⑤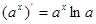 ;⑥
;⑥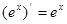 ; ⑦
; ⑦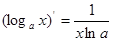 ;⑧
;⑧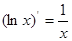
5、导数的运算法则
(1)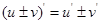 . (2)
. (2)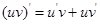 . (3)
. (3)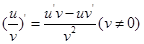 .
.
6、会用导数求单调区间、极值、最值
7、求函数 的极值的方法是:解方程
的极值的方法是:解方程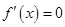 .当
.当 时:
时:
(1) 如果在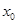 附近的左侧
附近的左侧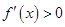 ,右侧
,右侧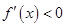 ,那么
,那么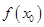 是极大值;
是极大值;
(2) 如果在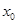 附近的左侧
附近的左侧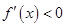 ,右侧
,右侧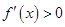 ,那么
,那么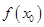 是极小值.
是极小值.
1.导数与单调性: 导数及其应用
(1)一般地,设函数 y = f ( x) 在某个区间可导,如果 f ′( x ) > 0 ,则 f ( x ) 为增函数;如果 f ′( x) < 0 ,则 f ( x) 为减函数;如果在某区间内恒有 f ′( x) = 0 ,则 f ( x) 为常数;
…… …… 余下全文
篇八 :高中数学知识点总结_导数的应用
导数的应用、复数
1.用导数研究函数的单调性。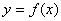 在区间
在区间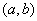 内可导,若
内可导,若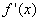 >0,则
>0,则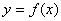 在
在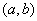 上递增;若
上递增;若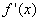 <0,则
<0,则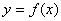 在
在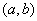 上递减. 注意:
上递减. 注意: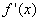 为正(负)是函数
为正(负)是函数 递增(减)充分不必要条件。如果函数f(x)在区间(a,b)内可导且不是常函数,上述结论可以改进为:f(x)在区间(a,b)上单调递增
递增(减)充分不必要条件。如果函数f(x)在区间(a,b)内可导且不是常函数,上述结论可以改进为:f(x)在区间(a,b)上单调递增
 ≥0在(a,b)上恒成立;f(x)在区间(a,b)上单调递减
≥0在(a,b)上恒成立;f(x)在区间(a,b)上单调递减
 ≤0在(a,b)上恒成立
≤0在(a,b)上恒成立
[举例1]已知函数 若
若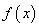 在
在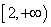 是增函数,求实数
是增函数,求实数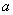 的范围。
的范围。
解析: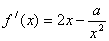 ≥0在
≥0在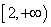 上恒成立
上恒成立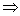
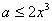 在
在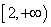 上恒成立
上恒成立
而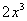 在
在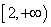 上的最小值为16,故
上的最小值为16,故 。
。
[举例2]已知定义在R上的函数y=f(x)的导函数f/(x)在R上也可导,且其导函数[f/(x)]/<0,
则y=f(x)的图象可能是下图中的 ( C )
…… …… 余下全文