篇一 :高一必修四函数及其函数图像总结
诱导公式:奇变偶不变,符号看象限。
①看是π/2的几倍,奇数倍变名,偶数倍不变。
②符号看变之前的。
③x永远当锐角。
一. 正弦函数:形如y=sin x的函数称为正弦函数。
性质: 1.定义域:R
2.值域:[-1,1]
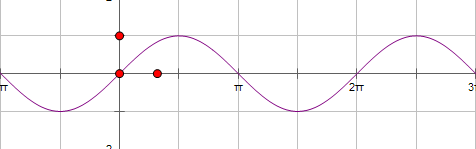 3.奇偶性:奇函数
3.奇偶性:奇函数
4.单调性:在(-π/2+2kπ, π/2+2kπ)上单调递增;
在(π/2+2kπ, 3π/2+2kπ)上单调递减。
5.周期: T=2π
6.对称轴:x=π/2+kπ
7.对称中心:(kπ,0)
8.最值: 当y=1时{x| x=π/2+kπ,k∈Z};
当y=-1时{x| x=-π/2+kπ,k∈Z}。
二. 余弦函数:形如y=cos x的函数称为余弦函数。
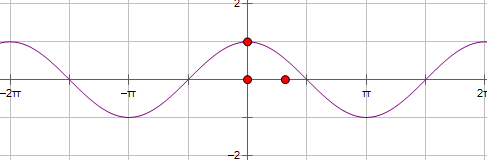 性质: 1.定义域:R
性质: 1.定义域:R
2.值域:[-1,1]
3.奇偶性:偶函数
4.单调性:在(-π+2kπ, 2kπ)上单调递增;
在(2kπ,π+2kπ)上单调递减。
…… …… 余下全文
篇二 :函数图像总结
高一数学函数图像知识点总结
一、函数图像知识点汇总
1.函数图象的变换
1平移变换
①水平平移:y=fx±aa>0的图象,可由y=fx的图象向左+或向右-平移a个单位而得到.
②竖直平移:y=fx±bb>0的图象,可由y=fx的图象向上+或向下-平移b个单位而得到.
2对称变换
①y=f-x与y=fx的图象关于y轴对称.
②y=-fx与y=fx的图象关于x轴对称.
③y=-f-x与y=fx的图象关于原点对称.
由对称变换可利用y=fx的图象得到y=|fx|与y=f|x|的图象.
①作出y=fx的图象,将图象位于x轴下方的部分以x轴为对称轴翻折到上方,其余部分不变,得到y=|fx|的图象;
②作出y=fx在y轴上及y轴右边的图象部分,并作y轴右边的图象关于y轴对称的图象,即得y=f|x|的图象.
3伸缩变换
①y=afxa>0的图象,可将y=fx图象上每点的纵坐标伸a>1时或缩a<1时到原来的a倍,横坐标不变.
②y=faxa>0的图象,可将y=fx的图象上每点的横坐标伸a<1时或缩a>1时到原来的倍,纵坐标不变.
…… …… 余下全文
篇三 :高中初等函数图像性质总结
高中函数图像性质总结
一、指数函数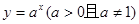
1、指数函数的图象和性质

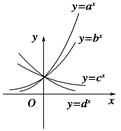 2、第一象限:底数越大,图像越高à
2、第一象限:底数越大,图像越高à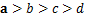
二、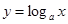
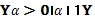
1、对数函数的图象和性质
2、当a>1时,a越大,图像越靠近x轴;
当0<a<1时,a越大,图像越远离x轴。
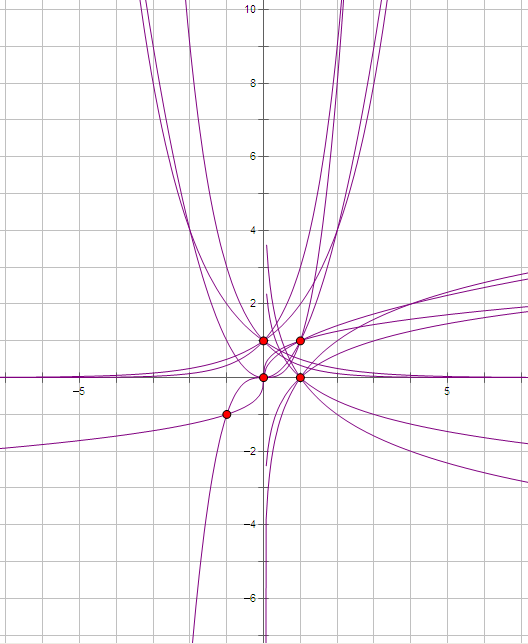
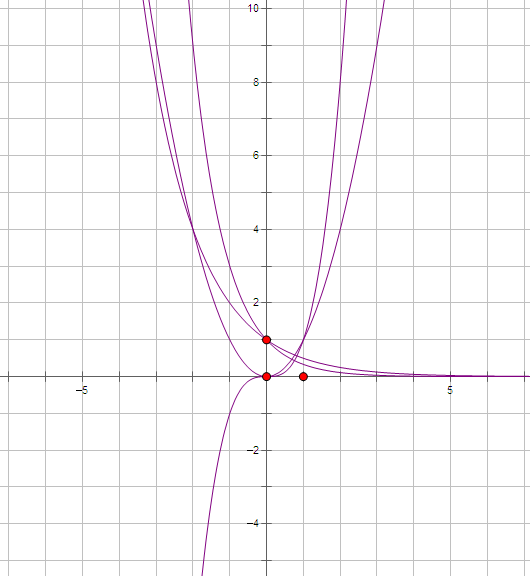
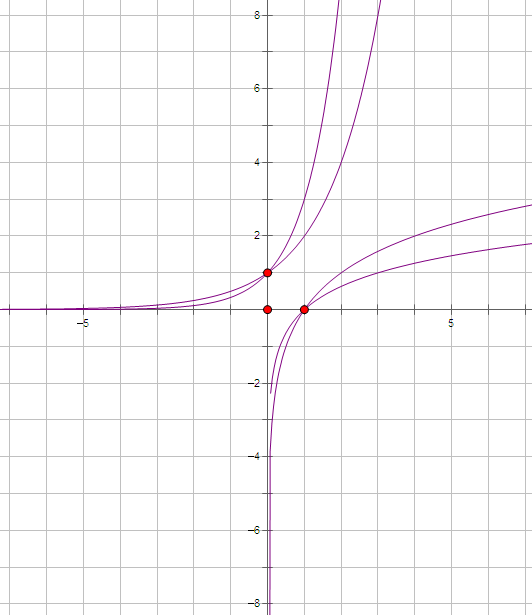
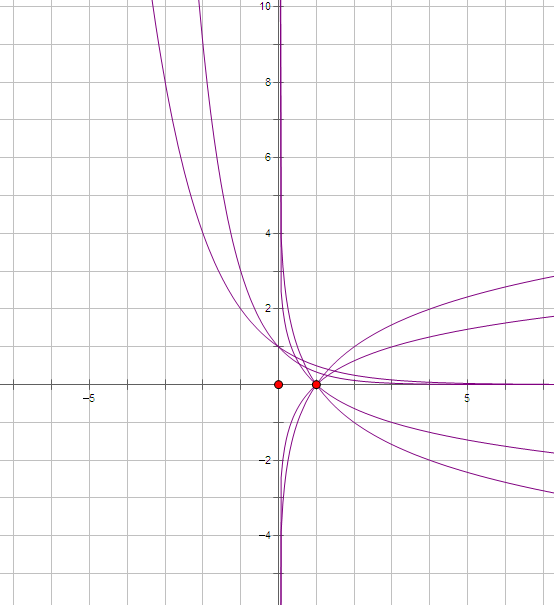
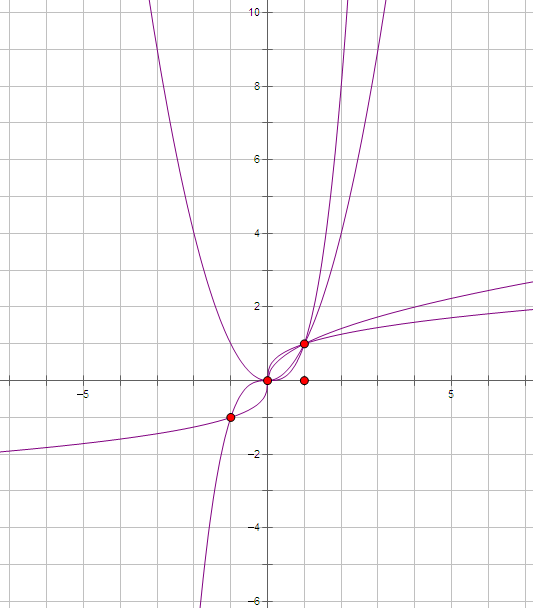
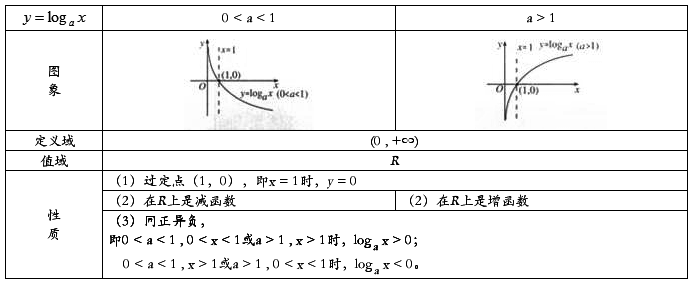
三、幂函数性质
1、所有的幂函数图象都过点(1,1)。除原点外,任何幂函数图像与坐标轴都不相交,任何幂函数图像都不过第四象限.;
注:当α>0时过定点(0,0)和(1,1);
当α<0时过定点(1,1)
2、α>0时,幂函数的图象都通过原点,并且在[0,+∞]上,是增函数
3、α<0时,幂函数的图象在区间(0,+∞)上是减函数.
4、任何两个幂函数最多有三个公共点
5、图像性质:
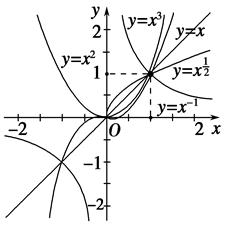
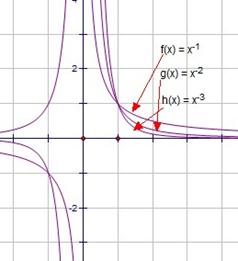
在第一象限幂函数图像表现为:
α>0时,α越大,图像越陡;
α<0时,α越大,图像越靠近y轴远离x轴。
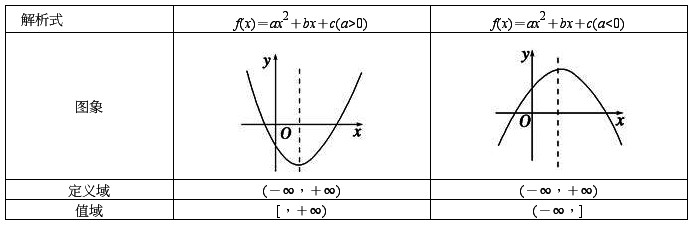
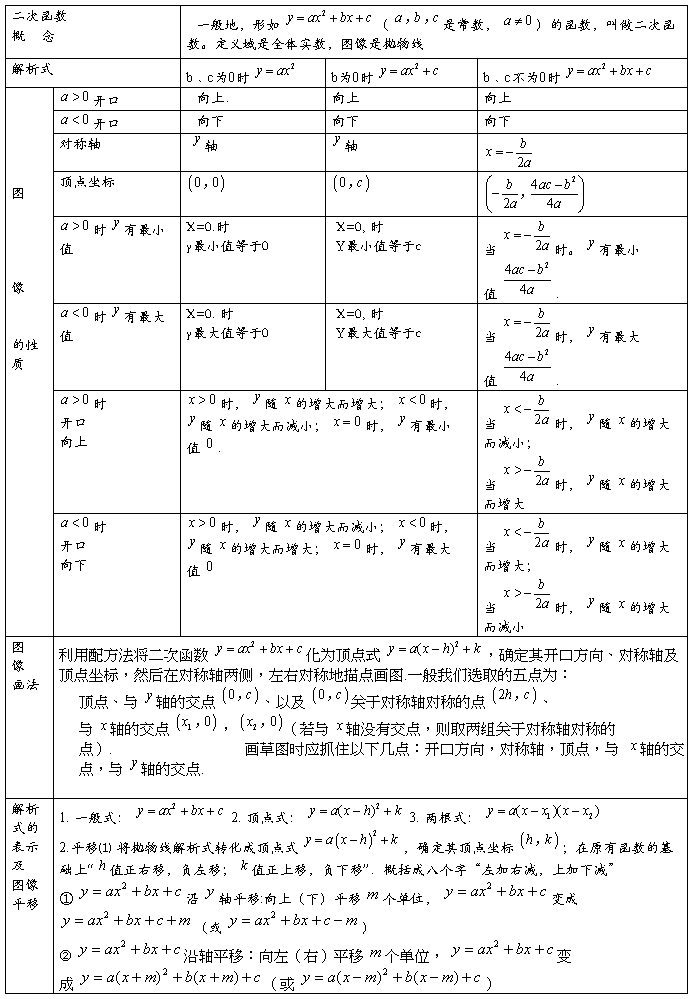
四、一元二次函数 :
:
1、图像和性质

2、一元二次函数表达式形式:
顶点式:f(x)=a(x-h)2+k,定点坐标(h,k)
分解式:f(x)=a(x-x1)(x-x2), 一元二次方程的两根为x1,x2
…… …… 余下全文
篇四 :一次函数及其图像知识点总结
第一节:函数
一、知识归纳
函数的概念
一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。
函数的三种表达式:
(1)图象;(2)表格;(3)关系式。
要使函数的解析式有意义。
函数的解析式是整式时,自变量可取全体实数;
②函数的解析式是分式时,自变量的取值应使分母≠0;
③函数的解析式是二次根式时,自变量的取值应使被开方数≥0。
④函数的解析式是三次根式时,自变量的取值应是一切实数。
(2)对于反映实际问题的函数关系,应使实际问题有意义。
4 常见函数关系式
几何
物理
生活
二、经典题型
题型考点一 求简单的函数关系式,识别自变量与因变量,给定自变量的值,相应地会求出函数的值。
例1.某市自来水公司为限制单位用水,每月只给某单位计划内用水300吨,计划内用水每吨收费0.5元,超计划部分每吨按0.8元收费。
⑴写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式:
①用水量小于等于3000吨 ;
…… …… 余下全文
篇五 :高一数学函数图像知识点总结
高一数学函数图像知识点总结
一、函数图像知识点汇总
1.函数图象的变换
(1)平移变换
①水平平移:y=f(x±a)(a>0)的图象,可由y=f(x)的图象向左(+)或向右(-)平移a个单位而得到.
②竖直平移:y=f(x)±b(b>0)的图象,可由y=f(x)的图象向上(+)或向下(-)平移b个单位而得到.
(2)对称变换
①y=f(-x)与y=f(x)的图象关于y轴对称.
②y=-f(x)与y=f(x)的图象关于x轴对称.
③y=-f(-x)与y=f(x)的图象关于原点对称.
由对称变换可利用y=f(x)的图象得到y=|f(x)|与y=f(|x|)的图象.
①作出y=f(x)的图象,将图象位于x轴下方的部分以x轴为对称轴翻折到上方,其余部分不变,得到y=|f(x)|的图象;
②作出y=f(x)在y轴上及y轴右边的图象部分,并作y轴右边的图象关于y轴对称的图象,即得y=f(|x|)的图象.
(3)伸缩变换
①y=af(x)(a>0)的图象,可将y=f(x)图象上每点的纵坐标伸(a>1时)或缩(a<1时)到原来的a倍,横坐标不变.
②y=f(ax)(a>0)的图象,可将y=f(x)的图象上每点的横坐标伸(a<1时)或缩(a>1时)到原来的倍,纵坐标不变.
(4)翻折变换
①作为y=f(x)的图象,将图象位于x轴下方的部分以x轴为对称轴翻折到上方,其余部分不变,得到y=|f(x)|的图象;
②作为y=f(x)在y轴上及y轴右边的图象部分,并作y轴右边的图象关于y轴对称的图象,即得y=f(|x|)的图象.
2.等价变换
可看出函数的图象为半圆.此过程可归纳为:(1)写出函数解析式的等价组;(2)化简等价组;(3)作图.
3.描点法作图
方法步骤:(1)确定函数的定义域;(2)化简函数的解析式;(3)讨论函数的性质即奇偶性、周期性、单调性、最值(甚至变化趋势);(4)描点连线,画出函数的图象.
注意:
一条主线
数形结合的思想方法是学习函数内容的一条主线,也是高考考查的热点.作函数图象首先要明确函数图象的形状和位置,而取值、列表、描点、连线只是作函数图象的辅助手段,不可本末倒置.
两个区别
(1)一个函数的图象关于原点对称与两个函数的图象关于原点对称不同,前者是自身对称,且为奇函数,后者是两个不同的函数对称.
(2)一个函数的图象关于y轴对称与两个函数的图象关于y轴对称也不同,前者也是自身对称,且为偶函数,后者也是两个不同函数的对称关系.
三种途径
明确函数图象形状和位置的方法大致有以下三种途径.
(1)图象变换:平移变换、伸缩变换、对称变换.
(2)函数解析式的等价变换.
(3)研究函数的性质.
二、例题解析

三、复习指导
函数图象是研究函数性质、方程、不等式的重要工具,是数形结合的基础,是高考考查的热点,复习时,应重点掌握几种基本初等函数的图象,并在审题、识图上多下功夫,学会分析“数”与“形”的结合点,把几种常见题型的解法技巧理解透彻
…… …… 余下全文
篇六 :函数及其图像知识总结
函数及其图像知识总结
一、平面直角坐标系
在平面内画两条互相垂直且有公共原点的数轴,就组成了平面直角坐标系。 坐标平面被x轴和y轴分割而成的四个部分,分别叫做第一象限、第二象限、第三象限、第四象限。
注意:x轴和y轴上的点,不属于任何象限。
二、不同位置的点的坐标的特征
1、各象限内点的坐标的特征
第一象限(+,+)第二象限(-,+)第三象限(-,-)第四象限(+,-)
2、坐标轴上的点的特征
在x轴上纵坐标为0,在y轴上横坐标为,原点坐标为(0,0)
3、两条坐标轴夹角平分线上点的坐标的特征
点P(x,y)在第一、三象限夹角平分线上x与y相等
点P(x,y)在第二、四象限夹角平分线上x与y互为相反数
4、和坐标轴平行的直线上点的坐标的特征
位于平行于x轴的直线上的各点的纵坐标相同。
位于平行于y轴的直线上的各点的横坐标相同。
5、关于x轴、y轴或远点对称的点的坐标的特征
点P与点p'关于x轴对称横坐标相等,纵坐标互为相反数
点P与点p'关于y轴对称纵坐标相等,横坐标互为相反数
点P与点p'关于原点对称横、纵坐标均互为相反数
6、点到坐标轴及原点的距离
…… …… 余下全文