函数 知识要点

一、本章知识网络结构：

F:A?B

二次函数

二、知识回顾： （一） 映射与函数 1. 映射与一一映射 2.函数

函数三要素是定义域，对应法则和值域，而定义域和对应法则是起决定作用的要素，因为这二者确定后，值域也就相应得到确定，因此只有定义域和对应法则二者完全相同的函数才是同一函数. 3.反函数

反函数的定义

设函数y?f(x)（x?A）的值域是C，根据这个函数中x，y的关系，用y把x表示出，得到x??(y). 若对于y在C中的任何一个值，通过x??(y)，x在A中都有唯一的值和它对应，那么，x??(y))就表示y是自变量，x是自变量y的函数，这样的函数x??(y) (y?C)叫做函数y?f(x)（x?A）的反函数，记作x?f习惯上改写成y?f（二）函数的性质 ⒈函数的单调性

定义：对于函数f(x)的定义域I内某个区间上的任意两个自变量的值x1,x2， ⑴若当x1?x2时，都有f(x1)?f(x2),则说f(x)在这个区间上是增函数；

?1

?1

(y),

(x)

⑵若当x1?x22时，都有f(x1)?f(x2),则说f(x) 在这个区间上是减函数.

若函数y?f(x)在某个区间是增函数或减函数，则就说函数y?f(x)在这一区间具有（严格的）单调性，这一区间叫做函数y?f(x)的单调区间.此时也说函数是这一区间上的单调函数. 2.函数的奇偶性

偶函数的定义：如果对于函数f(x)的定义域内任意一个，都有f(?x)?f(x)，那么函数

f(x)就叫做偶函数。

f(x)是偶函数?f(?x)?f(x)?f(?x)?f(x)?0?

f(?x)f(x)

?1（f(x)?0）。

奇函数的定义：如果对于函数f(x)的定义域内任意一个，都有f(?x)??f(x)，那么函数

f(x)就叫做奇函数。

f(x)是奇函数?f(?x)??f(x)?f(?x)?f(x)?0?

f(?x)f(x)

??1（f(x)?0）。

正确理解奇、偶函数的定义，必须把握好：

1、定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要不充分条件；

f(?x)?f(x)或f(?x)??f(x)是定义域上的恒等式。

2、奇函数的图象关于原点成中心对称图形，偶函数的图象关于y轴成轴对称图形。反之亦真。因此，也可以利用函数图象的对称性去判断偶函数的奇偶性。 3、奇函数在对称区间同增同减；偶函数在对称区间增减性相反。

4、如果f(x)是偶函数，则f(x)?f(x)，反之亦成立。若奇函数在x?0时有意义，则

f(0)?0。

7. 奇函数，偶函数： ⑴偶函数：f(?x)?f(x)

设(a,b)为偶函数上一点，则(?a,b)也是图象上一点. 偶函数的判定：两个条件同时满足

①定义域一定要关于y轴对称，例如：y?x?1在[?1,1)上不是偶函数. ②满足

f(?x)?f(x)，或f(?x)?f(x)?0

f(?x)??f(x)

2

，若

f(x)?0

时，

f(x)f(?x)

?1.

⑵奇函数：

设(a,b)为奇函数上一点，则(?a,?b)也是图象上一点. 奇函数的判定：两个条件同时满足 ①定义域一定要关于原点对称，例如：y②满足

f(?x)??f(x)，或f(?x)?f(x)?0

?x

3

在[1,?1)上不是奇函数.

f(x)?0

，若时，

f(x)f(?x)

??1

.

y轴对称

???8. 对称变换：①y = f（x）??y?f（?x）

x轴对称

???②y =f（x）??y??f（x）

????③y =f（x）?原点对称y??f（?x）

9. 判断函数单调性（定义）作差法：对带根号的一定要分子有理化，例如：

（x1?x2）(x1?x2) 2222

f(x1)?f(x2)?x1?b?x2?b?

2222 xx?b?x1?b在进行讨论.

10. 外层函数的定义域是内层函数的值域. 例如：已知函数f（x）= 1+

x1?x

的定义域为A，函数f[f(x)]的定义域是B，则集合A与集

合B之间的关系是 A?B . 解：f(x)的值域是11. 常用变换： ①

f(x?y)?f(x)f(y)?f(x?y)?

f(y)f(x)

f(x)f(y)

f(f(x))

的定义域B，f(x)的值域?

R

，故B?R，而A??x|x?1?，故A?B.

.

证：②

f(

f(x?y)?xy

?f(x)?f[(x?y)?y]?f(x?y)f(y)

)?f(x)?f(y)?f(x?y)?f(x)?f(y)

xy

xy

证：

f(x)?f(?y)?f()?f(y)

12. ⑴熟悉常用函数图象： 例：y?2

x

1x?21x1x?2

?x关于y轴对称. y?()?y?()?y?

()

222

y?2x?2x?1?y关于x轴对称.

2

⑵熟悉分式图象： 例：y

?2x?1x?3

?2?

7x?3

?

定义域{x|x?3,x?R}，

值域{y|y?2,y?R}→值域?x前的系数之比.

（三）指数函数与对数函数

指数函数y?a（a?0且a?1）的图象和性质

x

对数函数y?logax的图象和性质: 对数运算：

loga(M?N)?logaM?logaN??????⑴ loga

MN

n

?logaM?logaN

logaMlogaa

?nloga(?M)??????⑴

1n

logaM

??N

logaN

换底公式：logaN?

logbNlogba

推论：logab?logbc?logca?1

logaa2?logaa3???loga

1

2

n?1

an?logaan

1

（以上M?0,N?0,a?0,a?1,b?0,b?1,c?0,c?1,a1、a2、?、an?0，且?1） 注⑴：当a?0，b?0时，logc(a?b)?logc(?a)?logc(?b). ⑵：当M?0时，取“+”，当n是偶数时且M?0时，M

2

2

n

?0，而M?0，故取“—”.

例如：logax?2logax（因为2logax中x?0而logax中x?R，且x?0） ⑵y

?a

x

（a?0,a?1）与y

?log

a

?log

a

x

互为反函数.

当a?1时，y

x

的a值越大，越靠近x轴；当0?a?1时，则相反.

（四）方法总结

⑴.相同函数的判定方法：定义域相同且对应法则相同. ⑴对数运算：

⑵.函数表达式的求法：①定义法；②换元法；③待定系数法.

⑶.反函数的求法：先解x,互换x、y，注明反函数的定义域(即原函数的值域). ⑷.函数的定义域的求法：布列使函数有意义的自变量的不等关系式，求解即可求得函数的定义域.常涉及到的依据为①分母不为0；②偶次根式中被开方数不小于0；③对数的真数大于0，底数大于零且不等于1；④零指数幂的底数不等于零；⑤实际问题要考虑实际意义

等.

⑸.函数值域的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法.

⑹.单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1?x2；②判定f(x1)与

f(x2)的大小；③作差比较或作商比较.

⑺.奇偶性的判定法：首先考察定义域是否关于原点对称，再计算f(?x)与f(x)之间的关系：①f(?x)?f(x)为偶函数；f(?x)??f(x)为奇函数；②f(?x)?f(x)?0为偶；

f(?x)f(x)

f(?x)f(x)

f(?x)?f(x)?0为奇；③?1是偶；??1为奇函数.

⑻.图象的作法与平移：①据函数表达式，列表、描点、连光滑曲线；②利用熟知函数的图象的平移、翻转、伸缩变换；③利用反函数的图象与对称性描绘函数图象.

 

第二篇：高中三角函数知识点总结

三角函数  知识要点

1、角的表示

2. 角度与弧度

3、弧长公式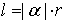：.       扇形面积公式：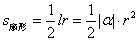

4、三角函数：设是一个任意角，在的终边上任取（异于原点的）一点P（x,y）P与原点的距离为r，则  ；  ；  ；  ；  ；. .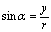

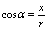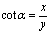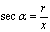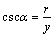5、三角函数在各象限的符号

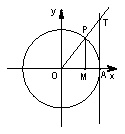
6、三角函数线

   正弦线：MP;   余弦线：OM;    正切线： AT.

7、三角函数的定义域：

8、同角三角函数的基本关系式：

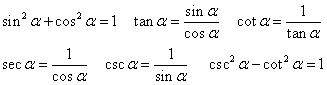
9、诱导公式：

 “奇变偶不变，符号看象限”

10、角与角之间的互换

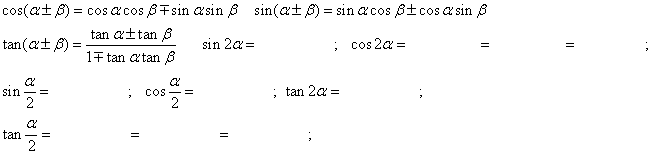积化和差：

和差化积：

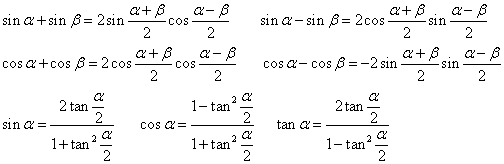
11. 正弦、余弦、正切、余切函数的图象的性质：

1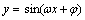的对称轴方程是     ，对称中心  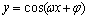   ；的对称轴方程是     ，对称中心  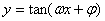   ；的对称中心     .

2当·；·.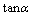

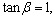
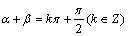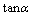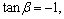
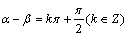3奇偶性的两个条件：一是              ，二是            

奇函数特有性质：若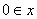的定义域，则一定有.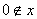（的定义域，则无此性质）

4不是周期函数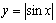；为周期函数（）；

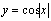是周期函数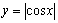；为周期函数（）；

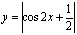的周期为。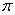

5 .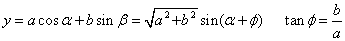

12、三角函数图象的作法：

1）、几何法：

2）、描点法及其特例——五点作图法（正、余弦曲线），三点二线作图法（正、余切曲线）.

3）、利用图象变换作三角函数图象：三角函数的图象变换有振幅变换、周期变换和相位变换等．

13、函数y＝Asin（ωx＋φ）的振幅     ，周期     ，频率     ，相位       初相

       （即当x＝0时的相位）．（当A＞0，ω＞0 时以上公式可去绝对值符号），

4、反三角函数：