最新高中数列知识点总结
数列知识点总结
第一部分 等差数列
一 定义式: 
二 通项公式: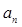
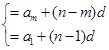
一个数列是等差数列的等价条件: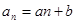 (a,b为常数),即
(a,b为常数),即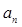 是关于n的一次函数,因为
是关于n的一次函数,因为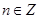 ,所以
,所以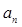 关于n的图像是一次函数图像的分点表示形式。
关于n的图像是一次函数图像的分点表示形式。
三 前n项和公式:
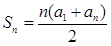 ………… ①
………… ①
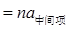 ………… ②
………… ②
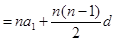 …… ③
…… ③
按照序号顺序,使用公式。即首选①公式解题,再选②、③
一个数列是等差数列的另一个充要条件: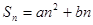 (a,b为常数,a≠0),即
(a,b为常数,a≠0),即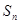 是关于n的二次函数,因为
是关于n的二次函数,因为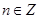 ,所以
,所以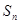 关于n的图像是二次函数图像的分点表示形式。
关于n的图像是二次函数图像的分点表示形式。
四 性质结论
(一)3或4个数成等差数列求数值时应按对称性原则设置,
如:3个数a-d,a,a+d; 4个数a-3d,a-d,a+d,a+3d
(二)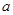 与
与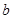 的等差中项
的等差中项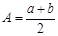 ;
;
在等差数列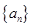 中,若
中,若 ,则
,则
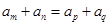 ;若
;若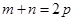 ,则
,则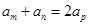 ;
;
(三)若等差数列的项数为2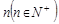 ,则
,则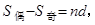
 ;
;
若等差数列的项数为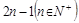 ,则
,则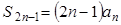 ,且
,且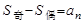 ,
,
(四)凡按一定规律和次序选出的一组一组的和仍然成等差数列。设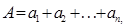 ,
,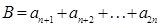 ,
,
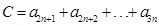 ,则有
,则有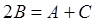 ;
;
(五)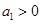 ,
,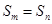 ,则前
,则前 (m+n为偶数)或
(m+n为偶数)或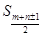 (m+n为奇
(m+n为奇
数)最大
第二部分 等比数列
一 定义: 成等比数列。
成等比数列。
二 通项公式: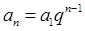 ,
,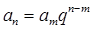
数列{an}是等比数列的一个等价条件是:
 当
当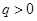 且
且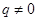 时,
时,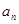 关于n的图像是指数函数图像的分点表示形式。
关于n的图像是指数函数图像的分点表示形式。
三 前n项和: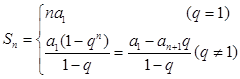 ;
;
(注意对公比的讨论)
四 性质结论:
(一)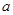 与
与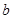 的等比中项
的等比中项
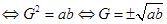 (
(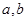 同号);
同号);
(二)在等比数列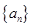 中,若
中,若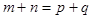 ,则
,则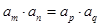 ;
;
若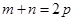 ,则
,则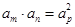 ;
;
(三)设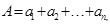 ,
,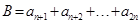 ,
,
 , 则有
, 则有
第三部分 求杂数列通项公式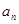
一 构造等比数列:凡是出现关于后项和前项的一次递推式都可以构造等比数列求通项公式。
第一类:
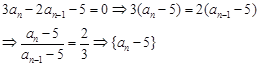
是公比为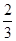 的等比数列
的等比数列 ,从而求出
,从而求出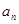 。
。
第二类:
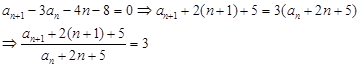

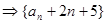
是公比为3的等比数列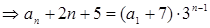 .
.
第三类: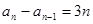 ,系数之比为1的时候用叠加法。
,系数之比为1的时候用叠加法。
第四类:既有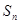 又有
又有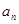 利用
利用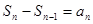 ,将所有S换成a,或者将所有a换成S。
,将所有S换成a,或者将所有a换成S。
第五类:关于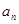 与
与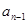 的二次式,或者
的二次式,或者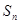 与
与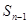 的二次式,先因式分解成一次式,再构造等比数列。
的二次式,先因式分解成一次式,再构造等比数列。
二 构造等差数列:递推式不能构造等比时,构造等差数列。
第一类:凡是出现分式递推式都可以构造等差数列来求通项公式,
例如: ,
,
两边取倒数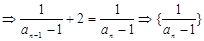 是公差为2的等差数列
是公差为2的等差数列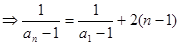 ,从而求出
,从而求出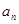 。
。
第二类:


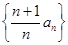 是公差为1的等差数列
是公差为1的等差数列

三 递推:即按照后项和前项的对应规律,再往前项推写对应式。
例如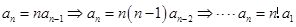
【注: 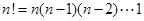 】
】
求通项公式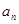 的题,不能够利用构造等比或者构造等差求
的题,不能够利用构造等比或者构造等差求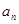 的时候,一般通过递推来求
的时候,一般通过递推来求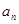 。
。
第四部分 求前n项和
一 裂项分组法:
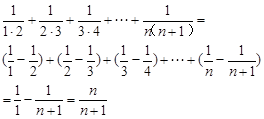 、
、
二 错位相减法:凡等差数列和等比数列对应项的乘积构成的数列求和时用此方法,
 求:
求:
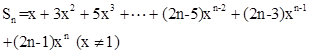
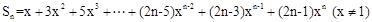 ①
①
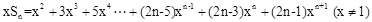 ②
②
①减②得:
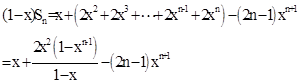
从而求出 。
。
错位相减法的步骤:
(1)将要求和的杂数列前后各写出三项,列出①式
(2)将①式左右两边都乘以公比q,得到②式
(3)用①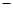 ②,错位相减
②,错位相减
(4)化简计算
三 倒序相加法:前两种方法不行时考虑倒序相加法
 1:等差数列求和:
1:等差数列求和:
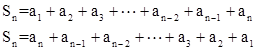
两式相加可得:
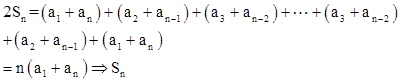
 2:设
2:设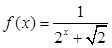 .利用课本中推导等差数列前n项和的公式的方法,可求得
.利用课本中推导等差数列前n项和的公式的方法,可求得
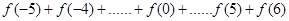 的值为_________.
的值为_________.
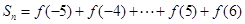 ①
①
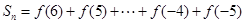 ②
②
①+②得
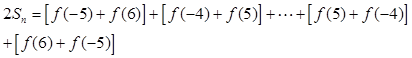
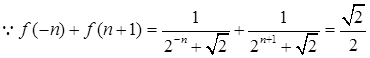 ,
,
∴
第二篇:高中数列知识点总结
数列知识点总结
第一部分 等差数列
一 定义式: 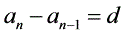
一个数列是等差数列的等价条件: (a,b为常数),即
(a,b为常数),即 是关于n的一次函数,因为
是关于n的一次函数,因为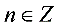 ,所以
,所以 关于n的图像是一次函数图像的分点表示形式。
关于n的图像是一次函数图像的分点表示形式。
二 通项公式: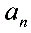
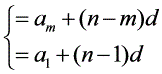
三 性质结论
1.3或4个数成等差数列求数值时应按对称性原则设置,如:3个数a-d,a,a+d; 4个数a-3d,a-d,a+d,a+3d
2. 与
与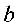 的等差中项
的等差中项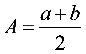 ;
;
在等差数列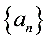 中,若
中,若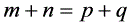 ,则
,则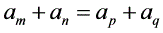 ;若
;若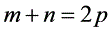 ,则
,则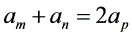 ;
;
3.若等差数列的项数为2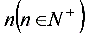 ,则
,则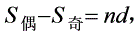
 ;
;
若等差数列的项数为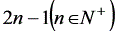 ,则
,则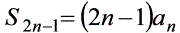 ,且
,且 ,
,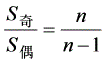
4.凡按一定规律和次序选出的一组一组的和仍然成等差数列。设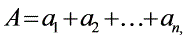
 ,
,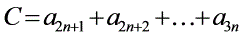 ,则有
,则有 ;
;
5. ,
, 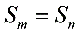 ,则前
,则前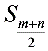 (m+n为偶数)或
(m+n为偶数)或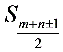 (m+n为奇数)最大
(m+n为奇数)最大
第二部分 等比数列
一 定义: 成等比数列。
成等比数列。
二 通项公式: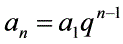 ,
,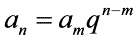
数列{an}是等比数列的一个等价条件是: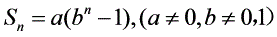 当
当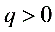 且
且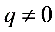 时,
时,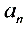 关于n的图像是指数函数图像的分点表示形式。
关于n的图像是指数函数图像的分点表示形式。
三 性质结论:
1.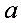 与
与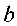 的等比中项
的等比中项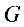
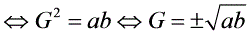 (
( 同号);
同号);
2.在等比数列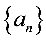 中,若
中,若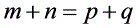 ,则
,则 ;若
;若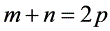 ,则
,则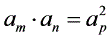 ;
;
3.设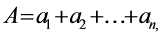 ,
,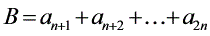 ,
,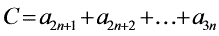 , 则有
, 则有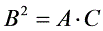
第三部分 求递推数列通项公式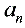
类型一:累加法 形如a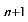 =a
=a + f (n), 其中f (n) 为关于n的多项式或指数形式(a
+ f (n), 其中f (n) 为关于n的多项式或指数形式(a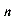 )或可裂项成差的分式形式.——可移项后叠加相消.
)或可裂项成差的分式形式.——可移项后叠加相消.
类型二: 累积法 形如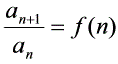 .其中f (n) =
.其中f (n) =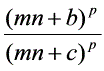 (p≠0,m≠0,b –c = km,k∈Z)或
(p≠0,m≠0,b –c = km,k∈Z)或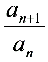 =kn(k≠0)或
=kn(k≠0)或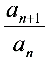 = km
= km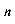 ( k ≠ 0, 0<m且m ≠ 1).
( k ≠ 0, 0<m且m ≠ 1).
类型三:形如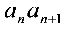 =
=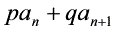 ,(pq ≠ 0).且
,(pq ≠ 0).且 的数列,——可通过倒数变形为基本数列问题.
的数列,——可通过倒数变形为基本数列问题.
当p = -q时,则有: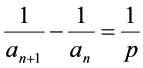 转化为等差数列;
转化为等差数列;
当p ≠ -q时,则有: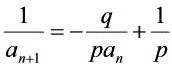 .同类型五转化为等比数列.
.同类型五转化为等比数列.
类型四:特征根法 形如a =pa
=pa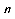 + q ,pq≠0 ,p、q为常数.
+ q ,pq≠0 ,p、q为常数.
当p =1时,为等差数列;
当p ≠1时,可在两边同时加上同一个数x,即a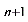 + x = pa
+ x = pa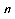 + q + x
+ q + x
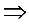 a
a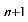 + x = p(a
+ x = p(a +
+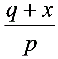 ), 令x =
), 令x =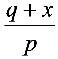 ∴x =
∴x =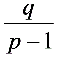 时,有a
时,有a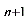 + x = p(a
+ x = p(a + x ),从而转化为等比数列 {a
+ x ),从而转化为等比数列 {a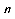 +
+ 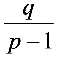 } 求解.
} 求解.
类型五:形如a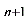 =pa
=pa + f (n),p≠0且 p为常数,f (n)为关于n的函数.
+ f (n),p≠0且 p为常数,f (n)为关于n的函数.
当p =1时,则 a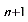 =a
=a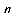 + f (n) 即类型一.
+ f (n) 即类型一.
当p ≠1时,f (n)为关于n的多项式或指数形式(a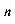 )或指数和多项式的混合形式.
)或指数和多项式的混合形式.
⑴若f (n)为关于n的多项式(f (n) = kn + b或kn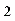 + bn + c,k、b、c为常数),——可用待定系数法转化为等比数列.
+ bn + c,k、b、c为常数),——可用待定系数法转化为等比数列.
⑵若f (n)为关于n的指数形式(a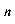 ).
).
①当p不等于底数a时,可转化为等比数列;
②当p等于底数a时,可转化为等差数列.
第四部分 求前n项和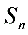
一:公式法求和直接用等差、等比数列的求和公式求和。
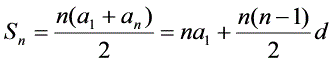
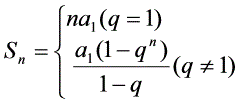 公比含字母时定要讨论
公比含字母时定要讨论
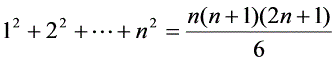

二.裂项相消法 这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的. 通项分解(裂项)如:
(1)1/n(n+1)=1/n-1/(n+1) (2)1/(2n-1)(2n+1)=1/2[1/(2n-1)-1/(2n+1)]
(3)1/n(n+1)(n+2)=1/2[1/n(n+1)-1/(n+1)(n+2)] (4)1/(√a+√b)=[1/(a-b)](√a-√b)
(5) n·n!=(n+1)!-n!(6)c/((n+a)(n+b))=(c/(a-b))*(1/( n+a)-1/(n+b))
小结:此类变形的特点是将原数列每一项拆为两项之后,其中中间的大部分项都互相抵消了。只剩下有限的几项。
注意: 余下的项具有如下的特点
1余下的项前后的位置前后是对称的。 2余下的项前后的正负性是相反的。
三.错位相减 如: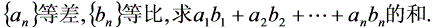
说明 求形如{an·bn}的数列的前n项和,若其中{an}成等差数列,{bn}成等比数列,则可采用推导等比数列求和公式的方法,即错位相减法,此方法体现了化归思想.
四:分组求和:把数列的每一项分成若干项,使其转化为等差或等比数列,再求和
五:合并求和:当通项公式中含有(-1)n,求和时可以对n的奇偶进行讨论,然后分情况求和.
例:1-2+3-4+5-6+……+(2n-1)-2n
可以先求出奇数项和偶数项的和,再相减。
但更好的方法是:(1-2)+(3-4)+(5-6)+……+[(2n-1)-2n]
8.其它求和法:如:归纳猜想法,奇偶法等
-
高中数列知识点总结归纳
一、等差数列1、等差数列定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个…
-
高中数列知识点总结
数列第一部分等差数列一定义式:an?an?1?d二通项公式:an???am?(n?m)d??a1?(n?1)d一个数列是等差数列的…
-
高中数列知识点总结及经典习题解答
用心辅导中心高中数学数列知识点及经典习题二、重难点击一、本章重点:数列的概念,等差数列,等比数列的定义,通项公式和前n项和公式及运…
-
最新高中数列知识点总结
数列知识点总结第一部分等差数列一定义式:an?an?1?d二通项公式:an???am?(n?m)d?a?(n?1)d?1一个数列是…
-
高中数列知识点总结
第五章数列知识点总结第一部分数列S11.Sn?a1?a2?a3???an??ai2.an???i?1?Sn?Sn?1题型一归纳、猜…
-
高中数列知识点总结归纳
一、等差数列1、等差数列定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个…
-
高中数学数列知识点总结(经典)
数列基础知识点和方法归纳1.等差数列的定义与性质定义:an?1?an?d(d为常数),an?a1??n?1?d等差中项:x,A,y…
-
高中数列知识点总结
数列知识点总结第一部分等差数列一定义式:an?an?1?d二通项公式:an???am?(n?m)d?a?(n?1)d?1一个数列是…
-
20xx年高考数学数列知识点大总结
20xx年高考数学数列知识点及题型大总结等差数列知识要点1.递推关系与通项公式递推关系:an?1?an?d通项公式:an?a1?(…
-
高中数学数列知识点总结(经典)
1.等差数列的定义与性质定义:an?1?an?d(d为常数),an?a1??n?1?d等差中项:x,A,y成等差数列?2A?x?y…
-
高中知识点总结
高中知识点总结2第五章细胞的能量供应与利用第一节降低化学反应活化能的酶1.细胞代谢:细胞中每时每刻都进行着许多化学反应。2.加热(…