导数复习知识点总结
导数知识点
一、导数相关概念
1.导数
函数y=f(x),如果自变量x在x 处有增量
处有增量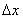 ,那么函数y相应地有增量
,那么函数y相应地有增量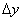 =f(x
=f(x +
+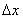 )-f(x
)-f(x ),比值
),比值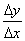 叫做函数y=f(x)在x
叫做函数y=f(x)在x 到x
到x +
+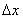 之间的平均变化率,即
之间的平均变化率,即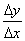 =
= 。如果当
。如果当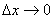 时,
时,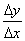 有极限,我们就说函数y=f(x)在点x
有极限,我们就说函数y=f(x)在点x 处可导,并把这个极限叫做f(x)在点x
处可导,并把这个极限叫做f(x)在点x 处的导数,记作f’(x
处的导数,记作f’(x )或y’|
)或y’|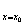 。
。
即f(x )=
)=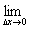
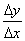 =
=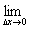
 。
。
说明:
(1)函数f(x)在点x 处可导,是指
处可导,是指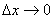 时,
时,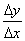 有极限。如果
有极限。如果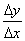 不存在极限,就说函数在点x
不存在极限,就说函数在点x 处不可导,或说无导数。
处不可导,或说无导数。
(2)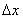 是自变量x在x
是自变量x在x 处的改变量,
处的改变量,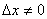 时,而
时,而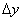 是函数值的改变量,可以是零。
是函数值的改变量,可以是零。
由导数的定义可知,求函数y=f(x)在点x 处的导数的步骤:
处的导数的步骤:
(1)求函数的增量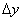 =f(x
=f(x +
+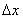 )-f(x
)-f(x );
);
(2)求平均变化率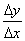 =
= ;
;
(3)取极限,得导数f’(x )=
)=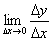 。
。
2.导数的几何意义
函数y=f(x)在点x 处的导数的几何意义是曲线y=f(x)在点p(x
处的导数的几何意义是曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率。也就是说,曲线y=f(x)在点p(x
))处的切线的斜率。也就是说,曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率是f’(x
))处的切线的斜率是f’(x )。相应地,切线方程为y-y
)。相应地,切线方程为y-y =f/(x
=f/(x )(x-x
)(x-x )。
)。
例:在函数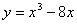 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于 的点中,坐标为整数的点的个数是 ( )
的点中,坐标为整数的点的个数是 ( )
A.3 B.2 C.1 D.0
3.几种常见函数的导数:
①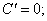 ②
② ③
③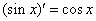 ; ④
; ④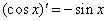 ;
;
⑤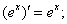 ⑥
⑥ ; ⑦
; ⑦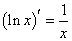 ; ⑧
; ⑧ .
.
例1:下列求导运算正确的是 ( )
A.(x+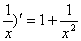 B.(log2x)′=
B.(log2x)′=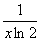
C.(3x)′=3xlog3e D. (x2cosx)′=-2xsinx
例2:设f0(x) = sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x) = fn′(x),n∈N,则f2005(x)= ( )
A.sinx B.-sinx C.cosx D.-cosx
4.导数的运算法则
法则1:两个函数的和(或差)的导数,等于这两个函数的导数的和(或差),
即: (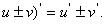
法则2:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个
函数乘以第二个函数的导数,即: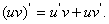
若C为常数,则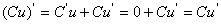 .即常数与函数的积的导数等于常数乘以函数的导数:
.即常数与函数的积的导数等于常数乘以函数的导数: 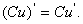
法则3:两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方: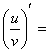
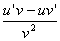 (v
(v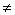 0)。
0)。
例:设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,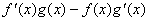 >0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
>0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
A. (-3,0)∪(3,+∞) B. (-3,0)∪(0, 3)
C. (-∞,- 3)∪(3,+∞) D. (-∞,- 3)∪(0, 3)
5.复合函数的导数
形如y=f
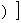 的函数称为复合函数。复合函数求导步骤:
的函数称为复合函数。复合函数求导步骤:
分解——>求导——>回代。
法则:y'|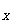 = y'|
= y'|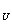 ·u'|
·u'|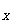 或者
或者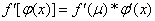 .
.
练习:求下列各函数的导数:
(1)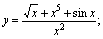 (2)
(2)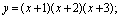
(3)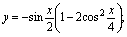 (4)
(4)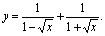
二、导数的应用
1.函数的单调性与导数
(1)设函数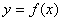 在某个区间(a,b)可导,如果
在某个区间(a,b)可导,如果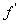

 ,则
,则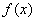 在此区间上为增函数;如果
在此区间上为增函数;如果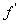
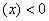 ,则
,则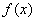 在此区间上为减函数。
在此区间上为减函数。
(2)如果在某区间内恒有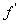
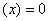 ,则
,则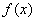 为常数。
为常数。
例:函数 是减函数的区间为 ( )
是减函数的区间为 ( )
A. B.
B. C.
C. D.(0,2)
D.(0,2)
2.极点与极值:
曲线在极值点处切线的斜率为0,极值点处的导数为0;曲线在极大值点左侧切线的斜率为正,右侧为负;曲线在极小值点左侧切线的斜率为负,右侧为正;
例:函数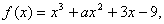 已知
已知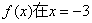 时取得极值,则
时取得极值,则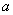 = ( )
= ( )
A.2 B.3 C.4 D.5
3.最值:
在区间[a,b]上连续的函数f 在[a,b]上必有最大值与最小值。但在开区间(a,b)内连续函数f(x)不一定有最大值,例如
在[a,b]上必有最大值与最小值。但在开区间(a,b)内连续函数f(x)不一定有最大值,例如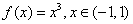 。
。
(1)函数的最大值和最小值是一个整体性的概念,最大值必须是整个区间上所有函数值中的最大值,最小值必须在整个区间上所有函数值中的最小值。
(2)函数的最大值、最小值是比较整个定义区间的函数值得出来的,函数的极值是比较极值点附件的函数值得出来的。函数的极值可以有多有少,但最值只有一个,极值只能在区间内取得,最值则可以在端点取得,有极值的未必有最值,有最值的未必有极值,极值可能成为最值,最值只要不在端点处必定是极值。
例:函数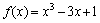 在闭区间[-3,0]上的最大值、最小值分别是 .
在闭区间[-3,0]上的最大值、最小值分别是 .
4.定积分
(1)概念:设函数f(x)在区间[a,b]上连续,用分点a=x0<x1<…<xi-1<xi<…xn=b把区间[a,b]等分成n个小区间,在每个小区间[xi-1,xi]上取任一点ξi(i=1,2,…n)作和式In= (ξi)△x(其中△x为小区间长度),把n→∞即△x→0时,和式In的极限叫做函数f(x)在区间[a,b]上的定积分,记作:
(ξi)△x(其中△x为小区间长度),把n→∞即△x→0时,和式In的极限叫做函数f(x)在区间[a,b]上的定积分,记作: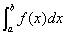 ,即
,即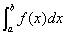 =
=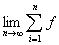 (ξi)△x。
(ξi)△x。
这里,a与b分别叫做积分下限与积分上限,区间[a,b]叫做积分区间,函数f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积式。
基本的积分公式:
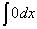 =C;
=C;
 =
=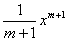 +C(m∈Q, m≠-1);
+C(m∈Q, m≠-1);
 dx=ln
dx=ln +C;
+C;
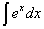 =
=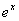 +C;
+C;
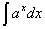 =
=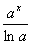 +C;
+C;
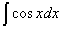 =sinx+C;
=sinx+C;
 =-cosx+C(表中C均为常数)。
=-cosx+C(表中C均为常数)。
 (2)定积分的性质
(2)定积分的性质
① (k为常数);
(k为常数);
②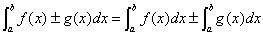 ;
;
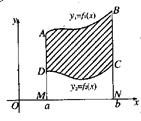 ③
③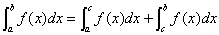 (其中a<c<b
(其中a<c<b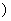 。
。
(3)定积分求曲边梯形面积
由三条直线x=a,x=b(a<b),x轴及一条曲线y=f(x)(f(x)≥0)围成的曲边梯的面积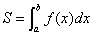 。
。
如果图形由曲线y1=f1(x),y2=f2(x)(不妨设f1(x)≥f2(x)≥0),及直线x=a,x=b(a<b)围成,那么所求图形的面积S=S曲边梯形AMNB-S曲边梯形DMNC=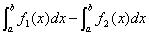 。
。
课后练习
1.求下列函数导数
(1)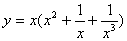 (2)
(2)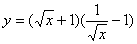 (3)
(3)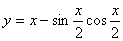
(4)y=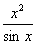 (5)y=
(5)y=
2.若曲线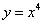 的一条切线
的一条切线 与直线
与直线 垂直,则
垂直,则 的方程为( )
的方程为( )
A.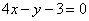 B.
B. C.
C.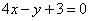 D.
D.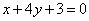
3.过点(-1,0)作抛物线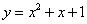 的切线,则其中一条切线为( )
的切线,则其中一条切线为( )
(A)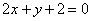 (B)
(B)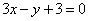 (C)
(C)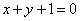 (D)
(D)
4.对于R上可导的任意函数f(x),若满足(x-1)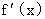 ³0,则必有( )
³0,则必有( )
A.f(0)+f(2)<2f(1) B. f(0)+f(2)£2f(1)
C.f(0)+f(2)³2f(1) D. f(0)+f(2)>2f(1)
5.函数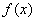 的定义域为开区间
的定义域为开区间 ,导函数
,导函数 在
在 内的图象如图所示,则函数
内的图象如图所示,则函数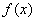 在开区间
在开区间 内有极小值点( )
内有极小值点( )
A.1个 B.2个 C.3个 D. 4个
6.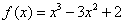 在区间
在区间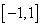 上的最大值是( )
上的最大值是( )
(A)-2 (B)0 (C)2 (D)4
7.设函数f(x)= 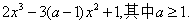
(Ⅰ)求f(x)的单调区间;
(Ⅱ)讨论f(x)的极值。
8.计算下列定积分的值
(1)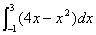
(2)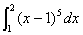 ;
;
(3) ;
;
(4)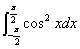 ;
;
8.已知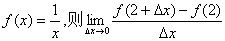 的值是( )
的值是( )
A. 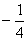 B. 2 C.
B. 2 C. 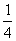 D. -2
D. -2
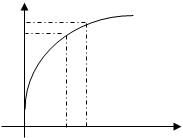
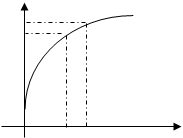
9.函数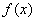 的图像如图所示,下列数值排序正确的是( )
的图像如图所示,下列数值排序正确的是( )
 A.
A. 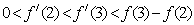 y
y
B. 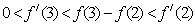
C. 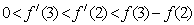
D. 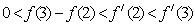 O 1 2 3 4 x
O 1 2 3 4 x
10.设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时, >0.且g(3)=0.则不等式f(x)g(x)<0的解集是
>0.且g(3)=0.则不等式f(x)g(x)<0的解集是
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0, 3)
C.(-∞,- 3)∪(3,+∞) D.(-∞,- 3)∪(0, 3)
11.已知函数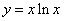 .(1)求这个函数的导数;(2)求这个函数在点
.(1)求这个函数的导数;(2)求这个函数在点 处的切线的方程.
处的切线的方程.
12.已知函数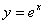 .
.
(1)求这个函数在点 处的切线的方程;
处的切线的方程;
(2)过原点作曲线y=ex的切线,求切线的方程.
13.判断下列函数的单调性,并求出单调区间:
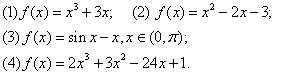
14.函数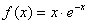 的一个单调递增区间是
的一个单调递增区间是
A. B.
B. 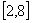 C.
C.  D.
D. 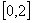
15.已知函数
(1)若函数的单调递减区间是(-3,1),则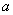 的是 .
的是 .
(2)若函数在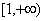 上是单调增函数,则
上是单调增函数,则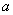 的取值范围是 .
的取值范围是 .
16.若函数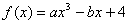 ,当
,当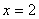 时,函数
时,函数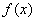 极值
极值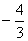 ,
,
(1)求函数的解析式;
(2)若函数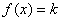 有3个解,求实数
有3个解,求实数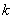 的取值范围.
的取值范围.
17.已知函数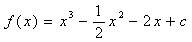 ,对xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围。
,对xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围。
第二篇:导数复习知识点总结
导数概念与运算知识清单
1.导数的概念
函数y=f(x),如果自变量x在x 处有增量
处有增量 ,那么函数y相应地有增量
,那么函数y相应地有增量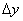 =f(x
=f(x +
+ )-f(x
)-f(x ),比值
),比值 叫做函数y=f(x)在x
叫做函数y=f(x)在x 到x
到x +
+ 之间的平均变化率,即
之间的平均变化率,即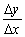 =
=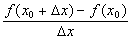 。如果当
。如果当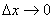 时,
时,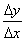 有极限,我们就说函数y=f(x)在点x
有极限,我们就说函数y=f(x)在点x 处可导,并把这个极限叫做f(x)在点x
处可导,并把这个极限叫做f(x)在点x 处的导数,记作f’(x
处的导数,记作f’(x )或y’|
)或y’|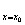 。
。
即f(x )=
)=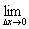
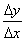 =
=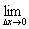
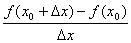 。
。
说明:(1)函数f(x)在点x 处可导,是指
处可导,是指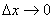 时,
时,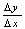 有极限。如果
有极限。如果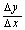 不存在极限,就说函数在点x
不存在极限,就说函数在点x 处不可导,或说无导数。
处不可导,或说无导数。
(2) 是自变量x在x
是自变量x在x 处的改变量,
处的改变量, 时,而
时,而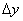 是函数值的改变量,可以是零。
是函数值的改变量,可以是零。
由导数的定义可知,求函数y=f(x)在点x 处的导数的步骤(可由学生来归纳):
处的导数的步骤(可由学生来归纳):
(1)求函数的增量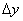 =f(x
=f(x +
+ )-f(x
)-f(x );
);
(2)求平均变化率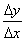 =
=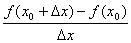 ;
;
(3)取极限,得导数f’(x )=
)= 。
。
2.导数的几何意义
函数y=f(x)在点x 处的导数的几何意义是曲线y=f(x)在点p(x
处的导数的几何意义是曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率。也就是说,曲线y=f(x)在点p(x
))处的切线的斜率。也就是说,曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率是f’(x
))处的切线的斜率是f’(x )。相应地,切线方程为y-y
)。相应地,切线方程为y-y =f/(x
=f/(x )(x-x
)(x-x )。
)。
3.几种常见函数的导数:
①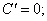 ②
②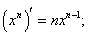 ③
③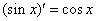 ; ④
; ④ ;
;
⑤ ⑥
⑥ ; ⑦
; ⑦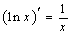 ; ⑧
; ⑧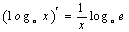 .
.
4.两个函数的和、差、积的求导法则
法则1:两个函数的和(或差)的导数,等于这两个函数的导数的和(或差),即: (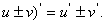
法则2:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个
函数乘以第二个函数的导数,即: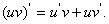
若C为常数,则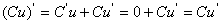 .即常数与函数的积的导数等于常数乘以函数的导数:
.即常数与函数的积的导数等于常数乘以函数的导数: 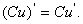
法则3:两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方:
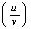 ‘=
‘=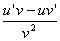 (v
(v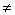 0)。
0)。
形如y=f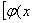
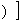 的函数称为复合函数。复合函数求导步骤:分解——求导——回代。法则:y'|
的函数称为复合函数。复合函数求导步骤:分解——求导——回代。法则:y'|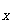 = y'|
= y'|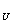 ·u'|
·u'|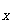
导数应用
1.单调性 单调区间:一般地,设函数 在某个区间可导,
在某个区间可导,
如果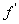
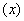
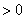 ,则
,则 为增函数;如果
为增函数;如果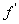
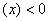 ,则
,则 为减函数;
为减函数;
如果在某区间内恒有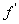
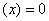 ,则
,则 为常数;
为常数;
2.极点与极值: 曲线在极值点处切线的斜率为0,极值点处的导数为0;曲线在极大值点左侧切线的斜率为正,右侧为负;曲线在极小值点左侧切线的斜率为负,右侧为正;
3.最值: 一般地,在区间[a,b]上连续的函数f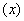 在[a,b]上必有最大值与最小值。
在[a,b]上必有最大值与最小值。
①求函数?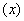 在(a,b)内的极值; ②求函数?
在(a,b)内的极值; ②求函数?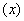 在区间端点的值?(a)、?(b);
在区间端点的值?(a)、?(b);
③将函数? 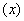 的各极值与?(a)、?(b)比较,其中最大的是最大值,其中最小的是最小值。
的各极值与?(a)、?(b)比较,其中最大的是最大值,其中最小的是最小值。
课前预习
1.求下列函数导数
(1) (2)
(2)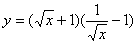 (3)
(3)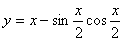
(4)y=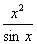 (5)y=
(5)y=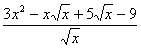
2.若曲线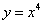 的一条切线
的一条切线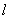 与直线
与直线 垂直,则
垂直,则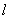 的方程为( )
的方程为( )
A.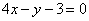 B.
B.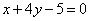 C.
C.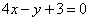 D.
D.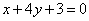
3.过点(-1,0)作抛物线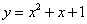 的切线,则其中一条切线为( )
的切线,则其中一条切线为( )
(A)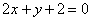 (B)
(B)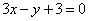 (C)
(C)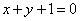 (D)
(D)
4.半径为r的圆的面积S(r)=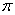 r2,周长C(r)=2
r2,周长C(r)=2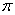 r,若将r看作(0,+∞)上的变量,则(
r,若将r看作(0,+∞)上的变量,则(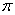 r2)`=2
r2)`=2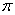 r 1,1式可以用语言叙述为:圆的面积函数的导数等于圆的周长函数。对于半径为R的球,若将R看作(0,+∞)上的变量,请你写出类似于
r 1,1式可以用语言叙述为:圆的面积函数的导数等于圆的周长函数。对于半径为R的球,若将R看作(0,+∞)上的变量,请你写出类似于
1的式子: ;
2式可以用语言叙述为: 。
5.曲线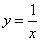 和
和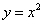 在它们交点处的两条切线与
在它们交点处的两条切线与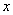 轴所围成的三角形面积是 。
轴所围成的三角形面积是 。
6.对于R上可导的任意函数f(x),若满足(x-1)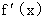 ³0,则必有( )
³0,则必有( )
A.f(0)+f(2)<2f(1) B. f(0)+f(2)£2f(1)
C.f(0)+f(2)³2f(1) D. f(0)+f(2)>2f(1)
7.函数 的定义域为开区间
的定义域为开区间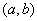 ,导函数
,导函数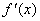 在
在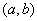 内的图象如图所示,则函数
内的图象如图所示,则函数 在开区间
在开区间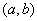 内有极小值点( )
内有极小值点( )
A.1个 B.2个 C.3个 D. 4个
8.已知函数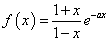 。(Ⅰ)设
。(Ⅰ)设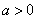 ,讨论
,讨论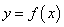 的单调性;(Ⅱ)若对任意
的单调性;(Ⅱ)若对任意 恒有
恒有 ,求
,求 的取值范围。
的取值范围。
9.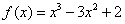 在区间
在区间 上的最大值是( )
上的最大值是( )
(A)-2 (B)0 (C)2 (D)4
10.设函数f(x)= 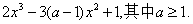
(Ⅰ)求f(x)的单调区间;
(Ⅱ)讨论f(x)的极值。
12.请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
14.(1)一物体按规律x=bt3作直线运动,式中x为时间t内通过的距离,媒质的阻力正比于速度的平方.试求物体由x=0运动到x=a时,阻力所作的功。
(2)抛物线y=ax2+bx在第一象限内与直线x+y=4相切.此抛物线与x轴所围成的图形的面积记为S.求使S达到最大值的a、b值,并求Smax.
典型例题
一 导数的概念与运算
EG:如果质点A按规律s=2t3运动,则在t=3 s时的瞬时速度为( )
A. 6m/s B. 18m/s C. 54m/s D. 81m/s
变式:定义在D上的函数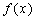 ,如果满足:
,如果满足: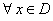 ,
,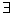 常数
常数 ,
,
都有 ≤M成立,则称
≤M成立,则称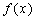 是D上的有界函数,其中M称为函数的上界.
是D上的有界函数,其中M称为函数的上界.
【文】(1)若已知质点的运动方程为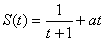 ,要使在
,要使在 上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
【理】(2)若已知质点的运动方程为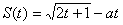 ,要使在
,要使在 上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
EG:已知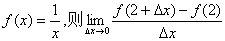 的值是( )
的值是( )
A. 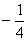 B. 2 C.
B. 2 C. 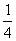 D. -2
D. -2
变式1: ( )
( )
A.-1 B.-2 C.-3 D.1
变式2: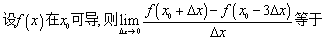 ( )
( )
A.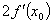 B.
B.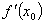 C.
C.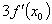 D.
D.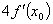
根据所给的函数图像比较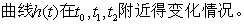
变式:函数 的图像如图所示,下列数值排序正确的是( )
的图像如图所示,下列数值排序正确的是( )
 A.
A. 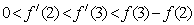 y
y
B. 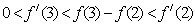
C. 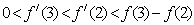
D. 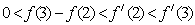 O 1 2 3 4 x
O 1 2 3 4 x
EG:求所给函数的导数:
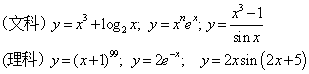 。
。
变式:设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,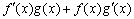 >0.且g(3)=0.则不等式f(x)g(x)<0的解集是
>0.且g(3)=0.则不等式f(x)g(x)<0的解集是
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0, 3)
C.(-∞,- 3)∪(3,+∞) D.(-∞,- 3)∪(0, 3)
EG:已知函数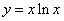 .(1)求这个函数的导数;(2)求这个函数在点
.(1)求这个函数的导数;(2)求这个函数在点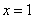 处的切线的方程.
处的切线的方程.
变式1:已知函数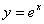 .
.
(1)求这个函数在点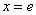 处的切线的方程;
处的切线的方程;
(2)过原点作曲线y=ex的切线,求切线的方程.
变式2:函数y=ax2+1的图象与直线y=x相切,则a=( )
A. 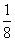 B.
B. 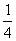 C.
C. 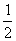 D. 1
D. 1
EG:判断下列函数的单调性,并求出单调区间:
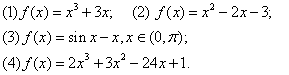
变式1:函数 的一个单调递增区间是
的一个单调递增区间是
A.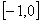 B.
B. 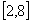 C.
C. 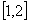 D.
D. 
变式2:已知函数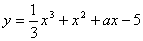
(1)若函数的单调递减区间是(-3,1),则 的是 .
的是 .
(2)若函数在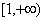 上是单调增函数,则
上是单调增函数,则 的取值范围是 .
的取值范围是 .
变式3: 设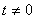 ,点P(
,点P( ,0)是函数
,0)是函数 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(Ⅰ)用 表示a,b,c;
表示a,b,c;
(Ⅱ)若函数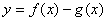 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求 的取值范围.
的取值范围.
EG:求函数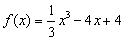 的极值.
的极值.
求函数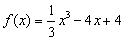 在
在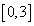 上的最大值与最小值..
上的最大值与最小值..
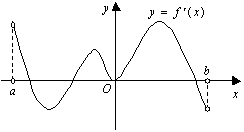 变式1: 函数
变式1: 函数 的定义域为开区间
的定义域为开区间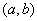 ,导函数
,导函数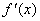 在
在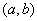 内的图象如图所示,则函数
内的图象如图所示,则函数 在开区间
在开区间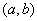 内有极小值点( )
内有极小值点( )
A.1个
B.2个
C.3个
D.4个

 变式2:已知函数
变式2:已知函数 在点
在点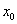 处取得极大值
处取得极大值 ,其导函数
,其导函数 的图象经过点
的图象经过点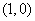 ,
,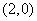 ,如图所示.求:
,如图所示.求:
(Ⅰ)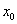 的值;(Ⅱ)
的值;(Ⅱ)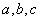 的值.
的值.
变式3:若函数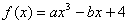 ,当
,当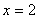 时,函数
时,函数 极值
极值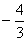 ,
,
(1)求函数的解析式;
(2)若函数 有3个解,求实数
有3个解,求实数 的取值范围.
的取值范围.
变式4:已知函数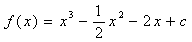 ,对xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围。
,对xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围。
EG:利用函数的单调性,证明: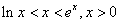
变式1:证明: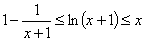 ,
,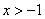
变式2:(理科)设函数f(x)=(1+x)2-ln(1+x)2.若关于x的方程f(x)=x2+x+a在[0,2]上恰好有两个相异的实根,求实数a的取值范围.
EG: 函数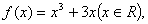 若
若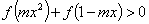 恒成立,求实数
恒成立,求实数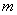 的取值范围
的取值范围
变式1:设函数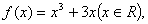 若
若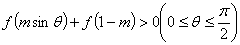 恒成立,求实数
恒成立,求实数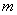 的取值范围.
的取值范围.
变式2:如图,曲线段OMB是函数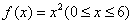 的图象,
的图象,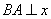 轴于点A,曲线段OMB上一点M
轴于点A,曲线段OMB上一点M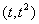 处的切线PQ交x轴于点P,交线段AB于点Q,
处的切线PQ交x轴于点P,交线段AB于点Q,
(1)若t已知,求切线PQ的方程 (2)求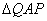 的面积的最大值
的面积的最大值
变式3:用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻折900角,再焊接而成,问该容器的高为多少时,容器的容积最大?最大的容积是多少?
变式4:某厂生产某种产品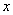 件的总成本
件的总成本 (万元),已知产品单价
(万元),已知产品单价
的平方与产品件数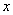 成反比,生产100件这样的产品单价为50万元,产量定为多少时总利润最大?
成反比,生产100件这样的产品单价为50万元,产量定为多少时总利润最大?
实战训练
1. 设函数f(x)在定义域内可导,y=f(x)的图象如右图所示,则导函数y=f ¢(x)的图象可能为( )
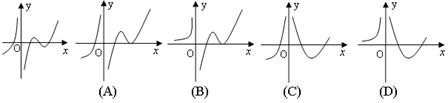
2. 已知曲线S:y=3x-x3及点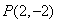 ,则过点P可向S引切线的条数为( )
,则过点P可向S引切线的条数为( )
(A)0 (B)1 (C)2 (D)3
3. C设S上的切点 求导数得斜率,过点P可求得:
求导数得斜率,过点P可求得: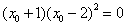 .
.
4. 函数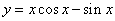 在下面哪个区间内是增函数( ).
在下面哪个区间内是增函数( ).
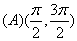
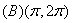

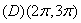
5. y=2x3-3x2+a的极大值为6,那么a等于( )
(A)6 (B)0 (C)5 (D)1
6. 函数f(x)=x3-3x+1在闭区间[-3,0]上的最大值、最小值分别是( )
(A)1,-1 (B)3,-17 (C)1,-17 (D)9,-19
7.设l1为曲线y1=sinx在点(0,0)处的切线,l2为曲线y2=cosx在点( ,0)处的切线,则l1与l2的夹角为___________.
,0)处的切线,则l1与l2的夹角为___________.
8. 设函数f (x)=x3+ax2+bx-1,若当x=1时,有极值为1,则函数g(x)=x3+ax2+bx的单调递减区间为 .
9.(07湖北)已知函数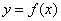 的图象在点
的图象在点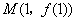 处的切线方程是
处的切线方程是 ,则
,则
10.(07湖南)函数 在区间
在区间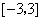 上的最小值是
上的最小值是
11.(07浙江)曲线 在点
在点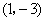 处的切线方程是 9.. 已知函数
处的切线方程是 9.. 已知函数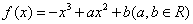
(Ⅰ)若函数 图像上任意一点处的切线的斜率小于1,求证:
图像上任意一点处的切线的斜率小于1,求证: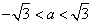 ;
;
(Ⅱ)若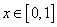 ,函数
,函数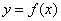 图像上任意一点处的切线的斜率为
图像上任意一点处的切线的斜率为 ,试讨论
,试讨论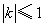 的充要条件。
的充要条件。
12.(07安徽)设函数f(x)=-cos2x-4tsin cos
cos +4t2+t2-3t+4,x∈R,其中
+4t2+t2-3t+4,x∈R,其中 ≤1,将f(x)的最小值记为g(t).
≤1,将f(x)的最小值记为g(t).
(Ⅰ)求g(t)的表达式;(Ⅱ)诗论g(t)在区间(-1,1)内的单调性并求极值.
实战训练B
1.(07福建)已知对任意实数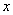 ,有
,有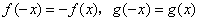 ,且
,且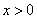 时,
时,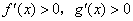 ,则
,则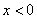 时( )
时( )
A.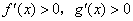 B.
B.
C.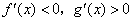 D.
D.
2.(07海南)曲线 在点
在点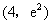 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A.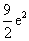 B.
B.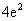 C.
C.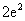 D.
D.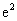
3.(07海南)曲线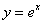 在点
在点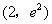 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A. B.
B.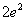 C.
C. D.
D.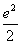
4.(07江苏)已知二次函数 的导数为
的导数为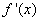 ,
,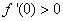 ,对于任意实数
,对于任意实数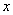 都有
都有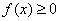 ,则
,则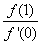 的最小值为( )
的最小值为( )
A. B.
B.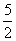 C.
C.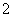 D.
D.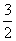
5.(07江西)5.若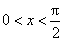 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A. B.
B.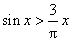 C.
C.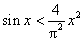 D.
D.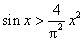
6.(07江西)若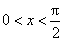 ,则下列命题正确的是( )
,则下列命题正确的是( )
A. B.
B.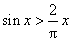 C.
C. D.
D.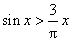
7.(07辽宁)已知 与
与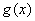 是定义在
是定义在 上的连续函数,如果
上的连续函数,如果 与
与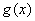 仅当
仅当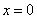 时的函数值为0,且
时的函数值为0,且 ,那么下列情形不可能出现的是( )
,那么下列情形不可能出现的是( )
A.0是 的极大值,也是
的极大值,也是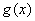 的极大值
的极大值
B.0是 的极小值,也是
的极小值,也是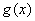 的极小值
的极小值
C.0是 的极大值,但不是
的极大值,但不是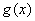 的极值
的极值
D.0是 的极小值,但不是
的极小值,但不是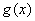 的极值
的极值
8.(07全国一)曲线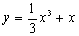 在点
在点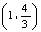 处的切线与坐标轴围成的三角形面积为( )
处的切线与坐标轴围成的三角形面积为( )
A. B.
B.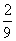 C.
C. D.
D.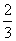
9.(07全国二)已知曲线 的一条切线的斜率为
的一条切线的斜率为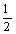 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.1 B.2 C.3 D.4
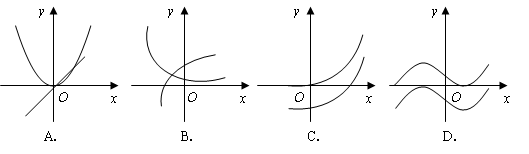
10.(07浙江)设 是函数
是函数 的导函数,将
的导函数,将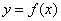 和
和 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )
11. (07北京) 是
是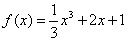 的导函数,则
的导函数,则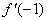 的值是
的值是
12.(07广东)函数 的单调递增区间是
的单调递增区间是
13.(07江苏)已知函数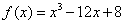 在区间
在区间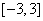 上的最大值与最小值分别为
上的最大值与最小值分别为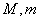 ,则
,则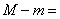
14.(07福建)设函数 .
.
(Ⅰ)求 的最小值
的最小值 ;
;
(Ⅱ)若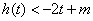 对
对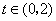 恒成立,求实数
恒成立,求实数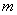 的取值范围.
的取值范围.
15.(07广东)已知 是实数,函数
是实数,函数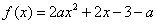 .如果函数
.如果函数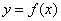 在区间
在区间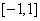 上有零点,求
上有零点,求 的取值范围.
的取值范围.
第三篇:高考复习导数知识点总结(文科使用)
导数知识点
一.考纲要求
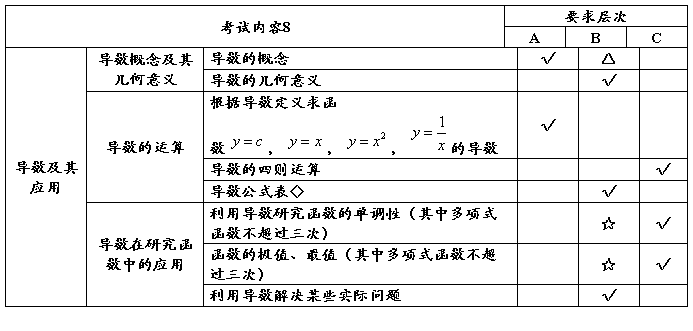
二.知识点
1.导数的几何意义:
函数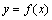 在点
在点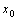 处的导数的几何意义就是曲线
处的导数的几何意义就是曲线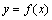 在点
在点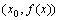 处的切线的斜率,也就是说,曲线
处的切线的斜率,也就是说,曲线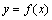 在点P
在点P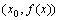 处的切线的斜率是
处的切线的斜率是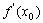 ,切线方程为
,切线方程为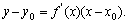
2.、几种常见函数的导数
①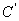
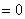 ;②
;②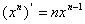 ; ③
; ③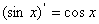 ;④
;④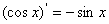 ;
;
⑤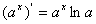 ;⑥
;⑥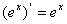 ; ⑦
; ⑦ ;⑧
;⑧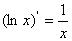
3.导数的运算法则
(1)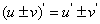 . (2)
. (2) . (3)
. (3) .
.
4. 极值的判别方法:(极值是在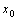 附近所有的点,都有
附近所有的点,都有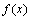 <
<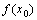 ,则
,则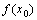 是函数
是函数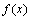 的极大值,极小值同理)
的极大值,极小值同理)
当函数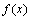 在点
在点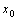 处连续时,
处连续时,
①如果在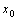 附近的左侧
附近的左侧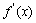 >0,右侧
>0,右侧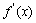 <0,那么
<0,那么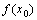 是极大值;
是极大值;
②如果在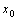 附近的左侧
附近的左侧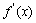 <0,右侧
<0,右侧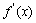 >0,那么
>0,那么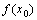 是极小值.
是极小值.
也就是说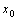 是极值点的充分条件是
是极值点的充分条件是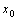 点两侧导数异号,而不是
点两侧导数异号,而不是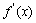 =0①. 此外,函数不可导的点也可能是函数的极值点②.当然,极值是一个局部概念,极值点的大小关系是不确定的,即有可能极大值比极小值小(函数在某一点附近的点不同).
=0①. 此外,函数不可导的点也可能是函数的极值点②.当然,极值是一个局部概念,极值点的大小关系是不确定的,即有可能极大值比极小值小(函数在某一点附近的点不同).
注①: 若点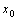 是可导函数
是可导函数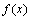 的极值点,则
的极值点,则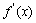 =0. 但反过来不一定成立. 对于可导函数,其一点
=0. 但反过来不一定成立. 对于可导函数,其一点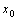 是极值点的必要条件是若函数在该点可导,则导数值为零.
是极值点的必要条件是若函数在该点可导,则导数值为零.
例如:函数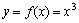 ,
, 使
使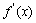 =0,但
=0,但 不是极值点.
不是极值点.
②例如:函数 ,在点
,在点 处不可导,但点
处不可导,但点 是函数的极小值点.
是函数的极小值点.
极值与最值区别:极值是在局部对函数值进行比较,最值是在整体区间上对函数值进行比较.
5.导数与单调性
(1) 一般地,设函数 y = f ( x) 在某个区间可导,如果 f ′( x ) > 0 ,则 f ( x ) 为增函数;如果 f ′( x) < 0 ,则 f ( x) 为减函数;如果在某区间内恒有 f ′( x) = 0 ,则 f ( x) 为常数;
(2)对于可导函数 y = f ( x) 来说, f ′( x ) > 0 是 f ( x ) 在某个区间上为增函数的充分非必要 条件, f ′( x ) < 0 是 f ( x ) 在某个区间上为减函数的充分非必要条件;
(3)利用导数判断函数单调性的步骤:
①求函数 f ( x ) 的导数 f ′( x ) ;②令 f ′( x ) > 0 解不等式,得 x 的范围,就是递增区间;③令 f ′( x) < 0 解不等式,得 x 的范围,就是递增区间。
-
高考复习导数知识点总结(文科使用)
导数知识点一.考纲要求二.知识点1.导数的几何意义:函数y?f(x)在点x0处的导数的几何意义就是曲线y?f(x)在点(x0,f(…
-
导数知识点总结及经典习题解答
导数知识点及习题讲解1.导数(导函数的简称)的定义:设x0是函数y?f(x)定义域的一点,如果自变量x在x0处有增量?x,则函数值…
-
导数知识点总结及经典习题解答 2
用心辅导中心高中数学导数知识点及习题讲解1.导数(导函数的简称)的定义:设x0是函数y?f(x)定义域的一点,如果自变量x在x0处…
-
导数知识点总结复习
经典例题剖析考点一:求导公式。例1.f?(x)是f(x)?13x?2x?1的导函数,则f?(?1)的值是3考点二:导数的几何意义。…
-
导数知识点总结
导数考试内容:导数的背影.导数的概念.多项式函数的导数.利用导数研究函数的单调性和极值.函数的最大值和最小值.考试要求:(1)了解…
-
南阳理工学院计科系信息安全导论知识点总结
第一章1.信息安全的定义:在技术上和管理上为数据处理系统建立的安全保护,保护信息系统的硬件、软件及相关数据不因偶然或者恶意的原因遭…
-
化工原理重要知识点总结
一基本概念1、连续性方程2、液体和气体混合物密度求取3、离心泵特性曲线的测定4、旋风分离器的操作原理5、传热的三种基本方式6、如何…
-
初二地理上册期终复习知识点总结
第一单元国土与居民第1课中国的疆域1、地理位置:海陆位置:我国位于亚洲东部,太平洋西岸;纬度位置:我国大部分位于北温带,南部小部分…
-
有机化学知识点总结
1.需水浴加热的反应有:(1)、银镜反应(2)、乙酸乙酯的水解(3)苯的硝化(4)糖的水解(5)、酚醛树脂的制取(6)固体溶解度的…
-
《桥梁工程》考试复习知识点总结
1.2.3.4.5.桥梁四个基本组成:上部结构,下部结构,支座和附属设施下部结构:桥墩,桥台,基础基本附属设施:桥面系,伸缩缝,桥…
-
假期社会实践总结
暑期社会实践体验近放暑假的时候,我们班开完班会,班长给我们每一个人发了一张大学生暑期实践活动登记表,要求我们利用暑期的时间投身到社…