高考数学基础知识总结:第十二章 概率与统计
高中数学:第十二章 概率与统计
考试内容:
抽样方法.总体分布的估计.
总体期望值和方差的估计.
考试要求:
(1)了解随机抽样了解分层抽样的意义,会用它们对简单实际问题进行抽样.
(2)会用样本频率分布估计总体分布.
(3)会用样本估计总体期望值和方差.
§12.概率与统计知识要点
一、随机变量.
1.随机试验的结构应该是不确定的.试验如果满足下述条件:
①试验可以在相同的情形下重复进行;②试验的所有可能结果是明确可知的,并且不止一个;③每次试验总是恰好出现这些结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果.
它就被称为一个随机试验.
2.离散型随机变量:如果对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.若ξ是一个随机变量,a,b是常数.则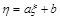 也是一个随机变量.一般地,若ξ是随机变量,
也是一个随机变量.一般地,若ξ是随机变量,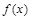 是连续函数或单调函数,则
是连续函数或单调函数,则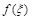 也是随机变量.也就是说,随机变量的某些函数也是随机变量.
也是随机变量.也就是说,随机变量的某些函数也是随机变量.
设离散型随机变量ξ可能取的值为: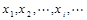
ξ取每一个值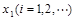 的概率
的概率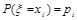 ,则表称为随机变量ξ的概率分布,简称ξ的分布列.
,则表称为随机变量ξ的概率分布,简称ξ的分布列.

有性质①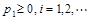 ;②
;②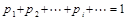 .
.
注意:若随机变量可以取某一区间内的一切值,这样的变量叫做连续型随机变量.例如: 即
即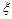 可以取0~5之间的一切数,包括整数、小数、无理数.
可以取0~5之间的一切数,包括整数、小数、无理数.
3.⑴二项分布:如果在一次试验中某事件发生的概率是P,那么在n次独立重复试验中这个事件恰好发生k次的概率是: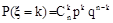 [其中
[其中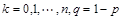 ]
]
于是得到随机变量ξ的概率分布如下:我们称这样的随机变量ξ服从二项分布,记作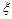 ~B(n·p),其中n,p为参数,并记
~B(n·p),其中n,p为参数,并记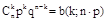 .
.
⑵二项分布的判断与应用.
①二项分布,实际是对n次独立重复试验.关键是看某一事件是否是进行n次独立重复,且每次试验只有两种结果,如果不满足此两条件,随机变量就不服从二项分布.
②当随机变量的总体很大且抽取的样本容量相对于总体来说又比较小,而每次抽取时又只有两种试验结果,此时可以把它看作独立重复试验,利用二项分布求其分布列.
4.几何分布:“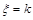 ”表示在第k次独立重复试验时,事件第一次发生,如果把k次试验时事件A发生记为
”表示在第k次独立重复试验时,事件第一次发生,如果把k次试验时事件A发生记为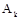 ,事A不发生记为
,事A不发生记为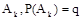 ,那么
,那么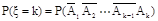 .根据相互独立事件的概率乘法分式:
.根据相互独立事件的概率乘法分式: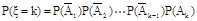
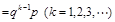 于是得到随机变量ξ的概率分布列.
于是得到随机变量ξ的概率分布列.

我们称ξ服从几何分布,并记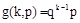 ,其中
,其中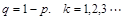
5.⑴超几何分布:一批产品共有N件,其中有M(M<N)件次品,今抽取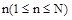 件,则其中的次品数ξ是一离散型随机变量,分布列为
件,则其中的次品数ξ是一离散型随机变量,分布列为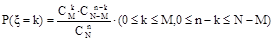 .〔分子是从M件次品中取k件,从N-M件正品中取n-k件的取法数,如果规定
.〔分子是从M件次品中取k件,从N-M件正品中取n-k件的取法数,如果规定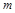 <
<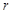 时
时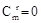 ,则k的范围可以写为k=0,1,…,n.〕
,则k的范围可以写为k=0,1,…,n.〕
⑵超几何分布的另一种形式:一批产品由a件次品、b件正品组成,今抽取n件(1≤n≤a+b),则次品数ξ的分布列为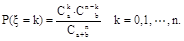 .
.
⑶超几何分布与二项分布的关系.
设一批产品由a件次品、b件正品组成,不放回抽取n件时,其中次品数ξ服从超几何分布.若放回式抽取,则其中次品数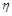 的分布列可如下求得:把
的分布列可如下求得:把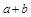 个产品编号,则抽取n次共有
个产品编号,则抽取n次共有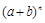 个可能结果,等可能:
个可能结果,等可能: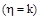 含
含 个结果,故
个结果,故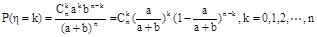 ,即
,即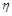 ~
~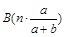 .[我们先为k个次品选定位置,共
.[我们先为k个次品选定位置,共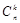 种选法;然后每个次品位置有a种选法,每个正品位置有b种选法]可以证明:当产品总数很大而抽取个数不多时,
种选法;然后每个次品位置有a种选法,每个正品位置有b种选法]可以证明:当产品总数很大而抽取个数不多时, ,因此二项分布可作为超几何分布的近似,无放回抽样可近似看作放回抽样.
,因此二项分布可作为超几何分布的近似,无放回抽样可近似看作放回抽样.
二、数学期望与方差.
1.期望的含义:一般地,若离散型随机变量ξ的概率分布为

则称 为ξ的数学期望或平均数、均值.数学期望又简称期望.数学期望反映了离散型随机变量取值的平均水平.
为ξ的数学期望或平均数、均值.数学期望又简称期望.数学期望反映了离散型随机变量取值的平均水平.
2.⑴随机变量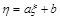 的数学期望:
的数学期望: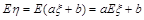
①当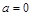 时,
时,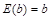 ,即常数的数学期望就是这个常数本身.
,即常数的数学期望就是这个常数本身.
②当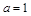 时,
时,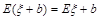 ,即随机变量ξ与常数之和的期望等于ξ的期望与这个常数的和.
,即随机变量ξ与常数之和的期望等于ξ的期望与这个常数的和.
③当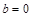 时,
时,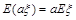 ,即常数与随机变量乘积的期望等于这个常数与随机变量期望的乘积.
,即常数与随机变量乘积的期望等于这个常数与随机变量期望的乘积.

⑵单点分布: 其分布列为:
其分布列为: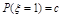 .
.
⑶两点分布: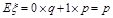 ,其分布列为:(p+q=1)
,其分布列为:(p+q=1)
⑷二项分布: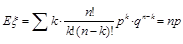 其分布列为
其分布列为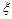 ~
~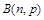 .(P为发生
.(P为发生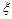 的概率)
的概率)
⑸几何分布: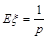 其分布列为
其分布列为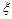 ~
~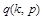 .(P为发生
.(P为发生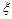 的概率)
的概率)
3.方差、标准差的定义:当已知随机变量ξ的分布列为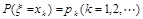 时,则称
时,则称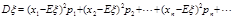 为ξ的方差.显然
为ξ的方差.显然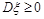 ,故
,故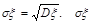 为ξ的根方差或标准差.随机变量ξ的方差与标准差都反映了随机变量ξ取值的稳定与波动,集中与离散的程度.
为ξ的根方差或标准差.随机变量ξ的方差与标准差都反映了随机变量ξ取值的稳定与波动,集中与离散的程度.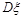 越小,稳定性越高,波动越小.
越小,稳定性越高,波动越小.
4.方差的性质.
⑴随机变量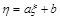 的方差
的方差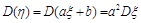 .(a、b均为常数)
.(a、b均为常数)

⑵单点分布: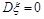 其分布列为
其分布列为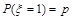
⑶两点分布: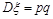 其分布列为:(p+q=1)
其分布列为:(p+q=1)
⑷二项分布: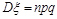
⑸几何分布: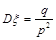
5.期望与方差的关系.
⑴如果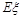 和
和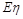 都存在,则
都存在,则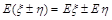
⑵设ξ和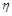 是互相独立的两个随机变量,则
是互相独立的两个随机变量,则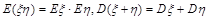
⑶期望与方差的转化: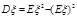 ⑷
⑷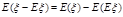 (因为
(因为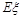 为一常数)
为一常数) .
.
三、正态分布.(基本不列入考试范围)
1.密度曲线与密度函数:对于连续型随机变量ξ,位于x轴上方,ξ落在任一区间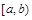 内的概率等于它与x轴.直线
内的概率等于它与x轴.直线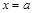 与直线
与直线 所围成的曲边梯形的面积
所围成的曲边梯形的面积
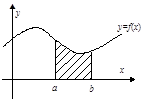 (如图阴影部分)的曲线叫ξ的密度曲线,以其作为
(如图阴影部分)的曲线叫ξ的密度曲线,以其作为
图像的函数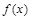 叫做ξ的密度函数,由于“
叫做ξ的密度函数,由于“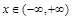 ”
”
是必然事件,故密度曲线与x轴所夹部分面积等于1.
2.⑴正态分布与正态曲线:如果随机变量ξ的概率密度为: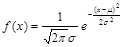 .(
.( 为常数,且
为常数,且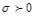 ),称ξ服从参数为
),称ξ服从参数为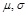 的正态分布,用
的正态分布,用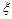 ~
~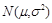 表示.
表示.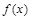 的表达式可简记为
的表达式可简记为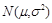 ,它的密度曲线简称为正态曲线.
,它的密度曲线简称为正态曲线.
⑵正态分布的期望与方差:若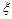 ~
~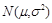 ,则ξ的期望与方差分别为:
,则ξ的期望与方差分别为: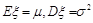 .
.
⑶正态曲线的性质.
①曲线在x轴上方,与x轴不相交.
②曲线关于直线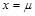 对称.
对称.
③当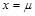 时曲线处于最高点,当x向左、向右远离时,曲线不断地降低,呈现出“中间高、两边低”的钟形曲线.
时曲线处于最高点,当x向左、向右远离时,曲线不断地降低,呈现出“中间高、两边低”的钟形曲线.
④当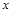 <
<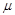 时,曲线上升;当
时,曲线上升;当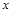 >
>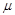 时,曲线下降,并且当曲线向左、向右两边无限延伸时,以x轴为渐近线,向x轴无限的靠近.
时,曲线下降,并且当曲线向左、向右两边无限延伸时,以x轴为渐近线,向x轴无限的靠近.
⑤当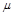 一定时,曲线的形状由
一定时,曲线的形状由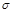 确定,
确定,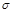 越大,曲线越“矮胖”.表示总体的分布越分散;
越大,曲线越“矮胖”.表示总体的分布越分散;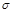 越小,曲线越“瘦高”,表示总体的分布越集中.
越小,曲线越“瘦高”,表示总体的分布越集中.
3.⑴标准正态分布:如果随机变量ξ的概率函数为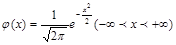 ,则称ξ服从标准正态分布.即
,则称ξ服从标准正态分布.即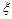 ~
~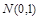 有
有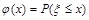 ,
,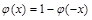 求出,而P(a<
求出,而P(a<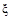 ≤b)的计算则是
≤b)的计算则是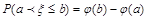 .
.
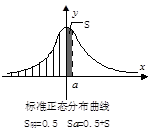 注意:当标准正态分布的
注意:当标准正态分布的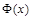 的X取0时,有
的X取0时,有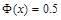 当
当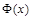 的X取大于0的数时,有
的X取大于0的数时,有 .比如
.比如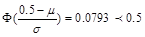 则
则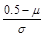 必然小于0,如图.
必然小于0,如图.
⑵正态分布与标准正态分布间的关系:若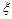 ~
~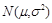 则ξ的分布函数通
则ξ的分布函数通
常用 表示,且有
表示,且有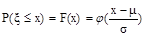 .
.
4.⑴“3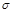 ”原则.
”原则.
假设检验是就正态总体而言的,进行假设检验可归结为如下三步:①提出统计假设,统计假设里的变量服从正态分布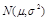 .②确定一次试验中的取值
.②确定一次试验中的取值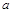 是否落入范围
是否落入范围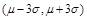 .③做出判断:如果
.③做出判断:如果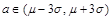 ,接受统计假设.如果
,接受统计假设.如果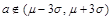 ,由于这是小概率事件,就拒绝统计假设.
,由于这是小概率事件,就拒绝统计假设.
⑵“3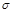 ”原则的应用:若随机变量ξ服从正态分布
”原则的应用:若随机变量ξ服从正态分布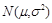 则ξ落在
则ξ落在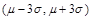 内的概率为99.7%亦即落在
内的概率为99.7%亦即落在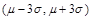 之外的概率为0.3%,此为小概率事件,如果此事件发生了,就说明此种产品不合格(即ξ不服从正态分布).
之外的概率为0.3%,此为小概率事件,如果此事件发生了,就说明此种产品不合格(即ξ不服从正态分布).
第二篇:高考数学基础知识总结:第十三章 极限
高中数学:第十三章 极限
考试内容:
教学归纳法.数学归纳法应用.
数列的极限.
函数的极限.根限的四则运算.函数的连续性.
考试要求:
(1)理解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题.
(2)了解数列极限和函数极限的概念.
(3)掌握极限的四则运算法则;会求某些数列与函数的极限.
(4)了解函数连续的意义,了解闭区间上连续函数有最大值和最小值的性质.
§13.极限 知识要点
1.⑴第一数学归纳法:①证明当n取第一个n0时结论正确;②假设当n?k(k?N?,k?n0)时,结论正确,证明当n?k?1时,结论成立.
⑵第二数学归纳法:设P(n)是一个与正整数n有关的命题,如果 ①当n?n0(n0?N?)时,P(n)成立;
②假设当n?k(k?N?,k?n0)时,P(n)成立,推得n?k?1时,P(n)也成立. 那么,根据①②对一切自然数n?n0时,P(n)都成立.
2.⑴数列极限的表示方法:
①liman?a;②当n??时,an?a. n??
⑵几个常用极限:
①limC?C(C为常数);②limn??n??1kn
③对于任意实常数,当|a|?1时,liman?0;当a?1时,若a=1,则liman?1;若a??1,n???0(k?N,k是常数); n??则liman?lim(?1)n不存在;当a?1时,liman不存在. n??n??n??
⑶数列极限的四则运算法则:
如果liman?a,limbb?b,那么 n??n??
①lim(an?bn)?a?b;②lim(an?bn)?a?b;③limn??n??ana?(b?0) n??bnb
特别地,如果C是常数,那么
lim(C?an)?limC?liman?Ca. n??n??n??
⑷数列极限的应用: 求无穷数列的各项和,特别地,当q?1时,无穷等比数列的各项和为S?a1(q?1).(化1?q循环小数为分数方法同上式)
注:并不是每一个无穷数列都有极限.
3.函数极限;
⑴当自变量x无限趋近于常数x0(但不等于x0)时,如果函数f(x)无限趋进于一个常数a,就是说当x趋近于x0时,函数f(x)的极限为a.记作limf(x)?a或当x?x0时,f(x)?a. x?x0
注:当x?x0时,f(x)是否存在极限与f(x)在x0处是否定义无关,因为x?x0并不要求x?x0.(当然,f(x)在x0是否有定义也与f(x)在x0处是否存在极限无关.?函数f(x)在x0有定义是limf(x)存在的既不充分又不必要条件.) x?x0
如P(x)???x?1x?1在x?1处无定义,但limP(x)存在,因为在x?1处左右极限均等于零. x?1??x?1x?1
⑵函数极限的四则运算法则:
如果limf(x)?a,limg(x)?b,那么 x?x0x?x0
①lim(f(x)?g(x))?a?b;②lim(f(x)?g(x))?a?b;③limx?x0x?x0x?x0f(x)a?(b?0) g(x)b特别地,如果C是常数,那么
lim(C?f(x))?Climf(x);lim[f(x)]n?[limf(x)]n(n?N?) x?x0x?x0x?x0x?x0
注:①各个函数的极限都应存在.
②四则运算法则可推广到任意有限个极限的情况,但不能推广到无限个情况. ⑶几个常用极限: ①lim1ilax?0(a>1);m; ?0;②limax?0(0<a<1)x???x???n??x
1sinxx1③lim) ?1?lim?1;④lim(1?)x?e,lim(1?x)x?e(e?2.71828183x?0x?0xx?0sinxx??x
4.函数的连续性:
⑴如果函数f(x),g(x)在某一点x?x0连续,那么函数f(x)?g(x),f(x)?g(x),f(x)(g(x)?0)g(x)在点x?x0处都连续.
⑵函数f(x)在点x?x0处连续必须满足三个条件:
①函数f(x)在点x?x0处有定义;②limf(x)存在;③函数f(x)在点x?x0处的极限值x?x0
等于该点的函数值,即limf(x)?f(x0). x?x0
⑶函数f(x)在点x?x0处不连续(间断)的判定:
如果函数f(x)在点x?x0处有下列三种情况之一时,则称x0为函数f(x)的不连续点. ①f(x)在点x?x0处没有定义,即f(x0)不存在;②limf(x)不存在;③limf(x)存在,但x?x0x?x0x?x0limf(x)?f(x0).
5.零点定理,介值定理,夹逼定理:
⑴零点定理:设函数f(x)在闭区间[a,b]上连续,且f(a)?f(b)?0.那么在开区间(a,b)内至少有函数f(x)的一个零点,即至少有一点?(a<?<b)使f(?)?0.
⑵介值定理:设函数f(x)在闭区间[a,b]上连续,且在这区间的端点取不同函数值,f(a)?A,f(b)?B,那么对于A,B之间任意的一个数C,在开区间(a,b)内至少有一点?,使得f(?)?C(a<?<b).
⑶夹逼定理:设当0?|x?x0|??时,有g(x)≤f(x)≤h(x),且limg(x)?limh(x)?A,则必x?x0x?x0有limf(x)?A. x?x0
注:|x?x0|:表示以x0为的极限,则|x?x0|就无限趋近于零.(?为最小整数)
6.几个常用极限: annk
?0(a?0);③limn?0(a?1,k为常数) ①limq?0,q?1;②limn???n???n!n???an
(lnn)klnn?0(??0,k为常数)④lim. ?0;⑤limn???n???nn?
-
统计学知识点总结
1统计的含义1统计工作即统计实践是指很据科学的方法从事统计设计收集整理分析研究和提供各种统计资料和统计咨询意见的活动的总称其成果是…
-
统计学知识点全归纳 全面、准确
统计学知识点汇总一统计学统计学是一门关于数据资料的收集整理分析和推断的科学二统计学的产生与发展1政治算术学派最早的统计学源于17世…
-
统计学知识点汇总
统计学知识点汇总第一章统计学是收集处理分析解析数据并从数据中得出结论的科学分类描述统计推断统计描述统计是研究数据收集处理和描述的统…
-
《统计》知识点精华总结
统计知识点精华总结1简单随机抽样的含义一般地设一个总体含有N个个体从中逐个不放回地抽取n个个体作为样本nN如果每次抽取时总体内的各…
-
统计学总结
单选20120简答题3515计算题65第一章导论一什么是统计包括统计研究的主要内容统计学是一门收集整理显示和分析统计数据的科学二与…
-
期中考试地理知识总结
第一章认识大洲第一节亚洲及欧洲1、亚洲、欧洲的地理位置3、亚洲气候特征4、欧洲气候特点:海洋性特征显著,温带海洋性气候和地中海气候…
-
逍遥游文言知识总结
《逍遥游》文言知识整理一、重要实词1、齐谐者,志怪者也(记载)2、亦若是则已矣(而已)3、而后乃今将图南(计划向南飞)4、我决起而…
-
《过秦论》知识总结
《过秦论》知识点总结Victorlu一、通假字①外连衡而斗诸侯/约从离衡(衡,通“横”)..②孝公既没(没,通“殁”,死亡).③合…
-
消防安全知识总结
“消防安全知识”团课总结20xx年x月26号,本班全体同学在懿德楼205教室举行了“消防安全知识”的主题团课,活动过程中,同学们十…
-
新课标高中物理学史知识总结
物理11.英国天文学家哈雷根据牛顿的万有引力定律正确地预言了哈雷彗星的回归。P52.美国气象学家洛伦兹发现,一个复杂系统初始条件的…
-
工程训练总结心得及报告
工程训练实验报告课程:工程训练学院:国防科技学院专业:辐射防护与环境工程姓名:黄顺立学号:20xx0566日期:20xx年x月x日…