数列通项经典总结
数学辅导-----《数列》(2)
【数列通项公式的求法】
一、定义法 —— 直接利用等差或等比数列的定义求通项。
(特征:适应于已知数列类型(等差or等比)的题目.)
2例.等差数列?an?是递增数列,前n项和为Sn,且a1,a3,a9成等比数列,S5?a5.求数列?an?的通项
公式.
二、公式法:求数列?an?的通项an可用公式
(特征:已知数列的前n项和Sn与an的关系)
例.已知数列?an?的前n项和Sn满足Sn?2an?(?1)n,n?1.求数列?an?的通项公式。
三、由递推式求数列通项法
类型1 特征:递推公式为an?1?an?f(n)
对策:把原递推公式转化为an?1?an?f(n),利用 求解。 例1. 已知数列?an?满足a1?
11,an?1?an?2,求an。 2n?n
n?1n对策:把原递推公式转化为an?1?f(n),利用 求解。 an
2nan,求an。 ,an?1?3n?1例2. 已知数列?an?满足a1?
类型3 特征:递推公式为an?1?pan?q(其中p,q均为常数) 对策:(利用构造法消去q)把原递推公式转化为由an?1?pan?q得an?pan?1?q(n?2)两式相减并a?an整理得n?1?p,构成数列?an?1?an?以a2?a1为首项,以p为公比的等比数列.求出an?an?1
?an?1?an?的通项再转化为类型1(累加法)便可求出an.
例3. 已知数列?an?中,a1?1,an?1?2an?3,求an.
解:法一:
解:法二:
n?1n对策:(利用构造法消去p)两边同时除以pn?1可得到an?1anf(n)an,令???bn,则pn?1pnpn?1pnbn?1?bn?f(n)n,再转化为类型1(累加法),求出之后得ba?pbn nnn?1p
例4.数列{an}的前n项和Sn.已知首项a1=3,且Sn?1+Sn=2an?1,试求此数列的通项公式an及前n项和Sn.
类型5 特征:递推公式为an?2?pan?1?qan(其中p,q均为常数)。
?s?t?p对策:先把原递推公式转化为an?2?san?1?t(an?1?san) 其中s,t满足?,再应用前面类型3st??q?
的方法求解。
例5. 已知数列?an?中,a1?1,a2?2,an?2?
21an?1?an,求an。 33
【巩固提高】 例8. 数列{an}满足a1=1,3an?1?an?7?0,求数列{an}的通项公式。
例9. 已知数列?an?满足a1?1,且an?1?3an?2,求an.
例10.已知数列?an?满足a1?1,an?3n?2an?1 (n?2),求an.
例11. 已知数列?an?满足a1?1,a2?3,an?2?3an?1?2an(n?N*).
例12. 数列?an?满足a1?2,a2?5,an?2?3an?1?2an=0,求数列{an}的通项公式。
(I)证明:数列?an?1?an?是等比数列;(II)求数列?an?的通项公式;
第二篇:求数列通项方法总结
求数列通项方法总结
一、课堂练习:
1.已知数列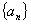 满足
满足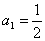 ,
,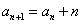 ,求
,求 ;
;
2.已知数列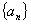 满足
满足 ,
,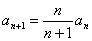 ,求
,求 ;
;
3.已知数列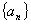 中,
中,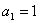 ,
,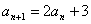 ,求
,求 ;
;
构造新数列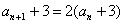 ,则数列
,则数列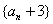 是首项为4,公比为2的等比数列
是首项为4,公比为2的等比数列
4.在数列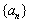 中,
中,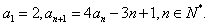 求
求 ;
;
构造新数列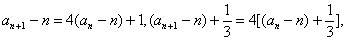 ,形式与3构造之前相同,则数列
,形式与3构造之前相同,则数列 的等比数列
的等比数列
5.已知数列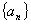 中,
中,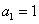 ,
,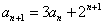 ,求
,求 ;
;
两边同时除以 ,得
,得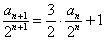 ,则数列
,则数列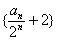 是首项为
是首项为 的等比数列
的等比数列
6.已知数列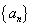 满足
满足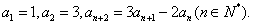 求数列
求数列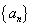 的通项公式;
的通项公式;
原式变形为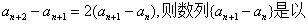 2为首项以2为公比的等比数列
2为首项以2为公比的等比数列
7.已知数列{an}满足: ,求数列
,求数列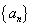 的通项公式;
的通项公式;
两边取倒数得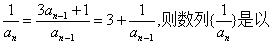 1为首项,3为公比的等比数列
1为首项,3为公比的等比数列
8.在数列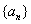 中,
中,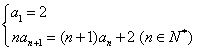 ,求通项公式
,求通项公式 ;
;
二式可以写成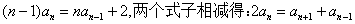 ,说明
,说明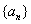 是等差数列
是等差数列
9.已知数列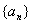 满足
满足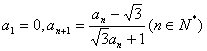 ,则
,则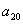 = ( )
= ( )
A.0 B.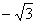 C.
C.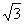 D.
D.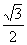
看到所求是具体的某一项的值,而又非等差等比数列,那么肯定具有周期关系,试前几项。
10.数列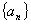 前n项和
前n项和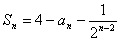 .(1)求
.(1)求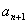 与
与 的关系;(2)求通项公式
的关系;(2)求通项公式 ;
;
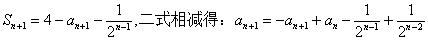
整理得: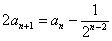 ,转化为
,转化为 ,则数列
,则数列 为等差数列
为等差数列
二、规律总结:
类型一:形如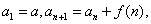 (其中
(其中 是可以求和的数列
是可以求和的数列 的通项公式)
的通项公式)
类型二:形如 (其中
(其中 是可以求积的数列
是可以求积的数列 的通项公式)
的通项公式)
类型三:形如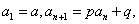 (其中
(其中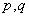 为常数,且
为常数,且 )
)
类型四:形如 (其中
(其中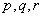 为常数,且
为常数,且 )
)
类型五:形如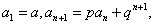 (其中
(其中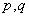 为常数,且
为常数,且 )
)
类型六:形如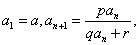 (其中
(其中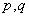 为常数,且
为常数,且 )
)
类型七:形如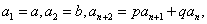 (其中
(其中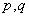 为常数,且
为常数,且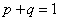 )
)
类型八:已知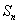 或
或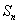 与
与 的关系式,求
的关系式,求
类型九:其他类型
课后反思:从学生情况看,学生对具体的给出数据的题目还能够在老师的帮助下完成,但是规律总结完成起来有很大困难,最后我旨在课堂上勉强完成了前3种类型的规律总结,后面就放弃了。
其实前3种类型我在前面讲课时已经渗透了解题方法,本以为上课时让学生能够很快地完成,但有一部分学生用了5分钟也未能完成,主要原因是缺乏对第n项往前推导的想象力,不知如何运用得到的通项关系;另一方面,学生虽然有了关系式,又懒得往后多写几项已看出规律。由此看出对于大多数学生推导规律的能力是很有限的。
从第4题开始,学生倍感困难,完全不知如何处理。个别数学很好的学生(郭键、刘佳)在处理这道题时出现了如下错误,(模仿第3题的做法)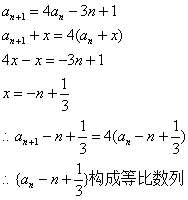
而且经过了相当长一段时间的自我纠错。
当总结第四题的规律时,刘傲给出了一个完美的规律表达:
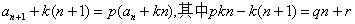 ,解决了上面所列的学生错误。
,解决了上面所列的学生错误。
在后续测试中我发现学生像第8题、第10题这样两式相减的题目也不能很好地掌握,主要问题是减后的代数变形不会往有利于解题的方向上去写。看来还是没有弄明白为什么要做这样的变化,对我上课所谈到的“把一个变换后的数列整体看成一个新的等差、等比数列”并没有在学生脑海中形成共识,对这个整体的构造有困难。
-
经典大总结
选择最淡的心事,诠释坎坷的人生引导语:人生就是一列开往坟墓的列车,路途上会有很多站口,没有一个人可以至始至终陪着你走完,你会看到来…
-
经典工作总结(最新)
江西财经大学职业技术学院————宿舍管理委员会学期工作总结时光荏苒,岁月如梭,风雨兼程中,宿舍管理委员会又告别了执着奋斗坚持的一年…
-
经典工作总结
工作总结时光飞逝,转眼间20xx年全年工作即将过去,20xx年已经向我们招手,回首全年工作,在各位领导的大力支持和领导下,我这一年…
-
人生经典总结
人生要结交两种人一良师二益友练就两项本领一做事让人感动二说话让人喜欢能吃得下两样东西一吃苦二吃亏自觉培养两种习惯一看好书二听演讲始…
-
经典的总结
1有些事我们总是弄不懂有些人我们总是猜不透有些道我们总是悟不尽有些理我们总是想不通有些坎我们总是跨不过有些伤我们总是治不好有些天我…
-
加薪申请书经典范文四篇
加薪申请书经典范文四篇文章整理:一览昆明英才网(有关专员)加薪是一场博弈,不只是张口那么简单,也许有的企业会给员工福利,工作一段时…
-
开展“诵读经典、传承文化、育德育人”主题活动方案
开展“诵读经典、传承文化、育德育人”主题活动方案为进一步推动我校中华经典诵读活动的深入开展,传承和弘扬中华民族优秀传统文化,增强民…
-
关于开展“少年梦_中华诵”经典诵读比赛的补充通知
关于开展“少年梦?中华诵”经典诵读比赛的补充通知各校:现将“少年梦.中华诵”国学经典诵读比赛的补充通知如下:一、比赛时间:更改为2…
-
夏店初中庆元旦暨中华经典诗文诵读大赛方案
夏店初中庆元旦暨中华经典诗文诵读大赛方案为了营造书香校园,弘扬中华传统优秀文化,传承中华古诗文这一珍贵的文化瑰宝,促进经典诵读,激…
-
经典诵读计划
如皋市下原初中20xx~20xx学年度经典诵读活动计划下原初中教科室一、指导思想自学校开展中华经典诵读活动以来,已经取得良好的教育…