初中数学函数知识总结归纳

1.常量和变量

在某变化过程中可以取不同数值的量，叫做变量.在某变化过程中保持同一数值的量或数，叫常量.

2.函数

设在一个变化过程中有两个变量x与y，如果对于x在某一范围的每一个值，y都有唯一的值与它对应，那么我们就说x是自变量，y是x的函数.

3.自变量的取值范围

?整式：自变量取一切实数.

?分式：分母不为零.

?偶次方根：被开方数为非负数.

?零指数与负整数指数幂：底数不为零.

4.函数值

对于自变量在取值范围内的一个确定的值，如当x＝a时，函数有唯一确定的对应值，这个对应值，叫做x＝a时的函数值.

5.函数的表示法

?解析法；?列表法；?图象法.

6.函数的图象

把自变量x的一个值和函数y的对应值分别作为点的横坐标和纵坐标，可以在平面直角坐标系内描出一个点，所有这些点的集合，叫做这个函数的图象. 由函数解析式画函数图象的步骤：

?写出函数解析式及自变量的取值范围；

?列表：列表给出自变量与函数的一些对应值；

?描点：以表中对应值为坐标，在坐标平面内描出相应的点；

?连线：用平滑曲线，按照自变量由小到大的顺序，把所描各点连接起来．

7.一次函数

?一次函数

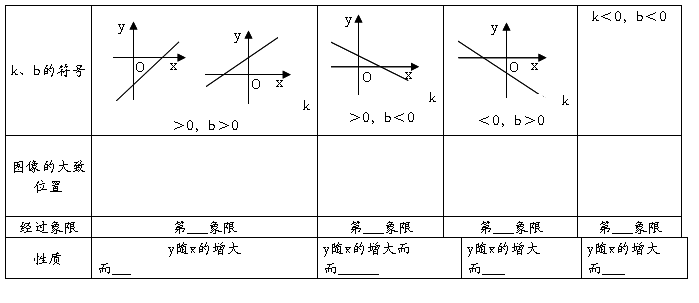
如果y＝kx＋b(k、b是常数且k≠0)，那么y就叫做x的一次函数.

特别地，当b＝0时，一次函数y＝kx＋b成为y＝kx(k是常数且k≠0)，这时，y就叫做x的正比例函数.

?一次函数的图象

一次函数y＝kx＋b的图象是一条经过(0，b)点和×点的直线.

特别地，正比例函数图象是一条经过原点的直线.

需要说明的是，在平面直角坐标系中，“直线”并不等同于“一次函数y＝kx＋b(k≠0)的图象”，因为还有直线y＝m(此时k＝0)和直线x＝n(此时k不存在)，它们不是一次函数图象.

?一次函数的性质

当k＞0时，y随x的增大而增大；当k＜0时，y随x的增大而减小. 直线y＝kx＋b与y轴的交点坐标为(0，b)，与x轴的交点坐标为×. ?用函数观点看方程(组)与不等式

①任何一元一次方程都可以转化为ax＋b＝0(a，b为常数且a≠0)的形式，所以解一元一次方程可以转化为：一次函数y＝kx＋b(k，b为常数且k≠0)，当y＝0时，求相应的自变量的值，从图象上看，相当于已知直线y＝kx＋b，确定它与x轴交点的横坐标.

②二元一次方程组对应两个一次函数，也对应两条直线，从“数”的角度看，解方程组相当于考虑自变量为何值时两个函数值相等，以及这两个函数值是何值；从“形”的角度看，解方程组相当于确定两条直线的交点的坐标.

③任何一元一次不等式都可以转化ax＋b＞0或ax＋b＜0(a、b为常数且a≠0)的形式，解一元一次不等式可以看做：当一次函数值大于0或小于0时，求自变量相应的取值范围.

8.反比例函数

?反比例函数

如果(k是常数且k≠0)，那么y就叫做x的反比例函数.

?反比例函数的图象

反比例函数的图象是一条双曲线.

?反比例函数的性质

①当k＞0时，图象的两个分支分别在第一、三象限内，在各自的象限内，y随x的增大而减小.

②当k＜0时，图象的两个分支分别在第二、四象限内，在各自的象限内，y随x的增大而增大.

③反比例函数图象关于直线y＝±x对称，关于原点对称.

?k的两种求法

①若点(x0，y0)在双曲线上，则k＝x0y0.

②k的几何意义

若双曲线上任一点A(x，y)，AB⊥x轴于B，则S△AOB×××.

?正比例函数和反比例函数的交点问题

若正比例函数y＝k1x(k1≠0)，反比例函数××，则

当k1k2＜0时，两函数图象无交点；

当k1k2＞0时，两函数图象有两个交点，坐标分别为××，由此可知，正反比例函数的图象若有交点，两交点一定关于原点对称.

9.二次函数

1.二次函数

如果y＝ax2＋bx＋c(a，b，c为常数且a≠0)，那么y就叫做x的二次函数. 几种特殊的二次函数：y＝ax2(a≠0)；y＝ax2＋c(ac≠0)；y＝ax2＋bx(ab≠0)；y＝a(x－h)2(a≠0).

2.二次函数的图象

二次函数y＝ax2＋bx＋c的图象是对称轴平行于y轴的一条抛物线.

由y＝ax2(a≠0)的图象，通过平移可得到y＝a(x－h)2＋k(a≠0)的图象．

3.二次函数的性质

二次函数y＝ax2＋bx＋c的性质对应在它的图象上，有如下性质：

?抛物线y＝ax2＋bx＋c的顶点是××，对称轴是直线×，顶点必在对称轴上；

?若a＞0，抛物线y＝ax2＋bx＋c的开口向上，因此，对于抛物线上的任意一点A（x,y)，当x＜×时，y随x的增大而减小；当x＞×时，y随x的增大而增大；当x＝×，y有最小值；

若a＜0，抛物线y＝ax2＋bx＋c的开口向下，因此，对于抛物线上的任意一点A (x，y)，当x＜×，y随x的增大而增大；当×时，y随x的增大而减小；当x＝×时，y有最大值；

?抛物线y＝ax2＋bx＋c与y轴的交点为(0，c)；

?在二次函数y＝ax2＋bx＋c中，令y＝0可得到抛物线y＝ax2＋bx＋c与x轴交点的情况：

Δ＜0时，抛物线y＝ax2＋bx＋c与x轴没有公共点．?＝0时，抛物线y＝ax2＋bx＋c与x轴只有一个公共点，即为此抛物线的顶点；当?＝b2－4ac＞0，抛物线y＝ax2＋bx＋c与x轴有两个不同的公共点，它们的坐标分别是×和×，这两点的距离为×；

4.抛物线的平移

抛物线y＝a(x－h)2＋k与y＝ax2形状相同，位置不同.把抛物线y＝ax2向上(下)、向左(右)平移，可以得到抛物线y＝a(x－h)2＋k.平移的方向、距离要根据h、k的值来决定.

 

第二篇：初中数学函数知识点归纳

初中数学函数板块的知识点总结与归类学习方法

初中数学知识大纲中，函数知识占了很大的知识体系比例，学好了函数，掌握了函数的基本性质及其应用，真正精通了函数的每一个模块知识，会做每一类函数题型，就读于中考中数学成功了一大半，数学成绩自然上高峰，同时，函数的思想是学好其他理科类学科的基础。

  初中数学从性质上分，可以分为：一次函数、反比例函数、二次函

数和锐角三角函数，下面介绍各类函数的定义、基本性质、函数图象及函数应用思维方式方法。

一、一次函数

  1. 定义：在定义中应注意的问题y＝kx＋b中，k、b为常数，且k≠0，x的指数一定为1。

  2. 图象及其性质

    （1）形状、直线

   

   

   

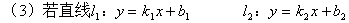
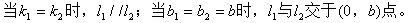
    （4）当b>0时直线与y轴交于原点上方；当b<0时，直线与y轴交于原点的下方。

    （5）当b=0时，y＝kx（k≠0）为正比例函数，其图象是一过原点的直线。

    （6）二元一次方程组与一次函数的关系：两一次函数图象的交点的坐标即为所对应方程组的解。

  3. 应用：要点是（1）会通过图象得信息；（2）能根据题目中所给的信息写出表达式。

（二）反比例函数

  1. 定义：

 

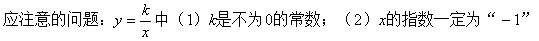
  2. 图象及其性质：

    （1）形状：双曲线

   

 

    （4）过图象上任一点作x轴与y轴的垂线与坐标轴构成的矩形面积为|k|。

 

二、二次函数

  1. 定义：应注意的问题

    （1）在表达式y＝ax²＋bx＋c中（a、b、c为常数且a≠0）

    （2）二次项指数一定为2

  2. 图象：抛物线

  3. 图象的性质：分五种情况可用表格来说明

  4. 应用：

    （1）最大面积；（2）最大利润；（3）其它

 平面直角坐标系、函数及其图像

【知识梳理】

一、平面直角坐标系

1. 坐标平面上的点与有序实数对构成一一对应；

2. 各象限点的坐标的符号；

3. 坐标轴上的点的坐标特征．

4. 点P（a，b）关于 对称点的坐标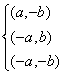

5.两点之间的距离

 

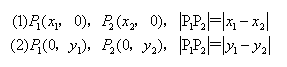
6.线段AB的中点C，若  则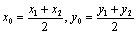

二、函数的概念

1.概念：在一个变化过程中有两个变量x与y，如果对于x的每一个值，y都有唯一的值与它对应，那么就说x是自变量，y是x 的函数.

2.自变量的取值范围： （1）使解析式有意义  （2）实际问题具有实际意义

3.函数的表示方法； （1）解析法   （2）列表法       （3）图象法

【思想方法】    数形结合

     一次函数图象和性质

【知识梳理】

1．正比例函数的一般形式是y=kx(k≠0)，一次函数的一般形式是y=kx+b(k≠0).

2. 一次函数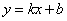的图象是经过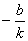（，0）和（0，b）两点的一条直线.

3. 一次函数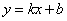的图象与性质

【思想方法】                      数形结合                                                 

   反比例函数图象和性质

【知识梳理】

1．反比例函数：一般地，如果两个变量x、y之间的关系可以表示成y＝          

或         （k为常数，k≠0）的形式，那么称y是x的反比例函数．

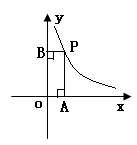
2. 反比例函数的图象和性质

3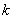．的几何含义：反比例函数y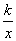＝ (k≠0)中比例系数k的几何意义，即过双曲线y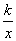＝ (k≠0)上任意一点P作x轴、y轴垂线，设垂足分别为A、B，则所得矩形OAPB的面积为      .

【思想方法】                                数形结合

                 二次函数图象和性质

【知识梳理】

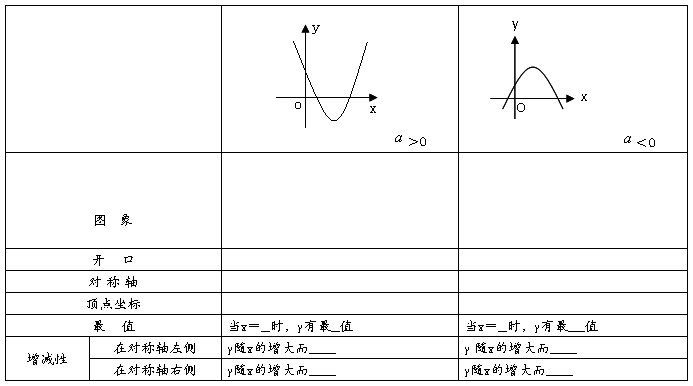
1. 二次函数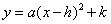的图像和性质

锐角三角函数

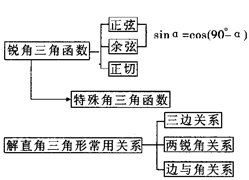
【思想方法】

1. 常用解题方法——设k法

2. 常用基本图形——双直角

【例题精讲】                                                     

例题1.在△ABC中，∠C=90°．

（1）若cosA=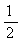，则tanB=______;（2）若cosA=，则tanB=______．

例题2.（1）已知：cosα=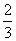，则锐角α的取值范围是（  ）

        A．0°<α<30°           B．45°<α<60°

        C．30°<α<45°          D．60°<α<90°

   （2）当45°<θ<90°时，下列各式中正确的是（  ）

        A．tanθ>cosθ>sinθ     B．sinθ>cosθ>tanθ

        C．tanθ>sinθ>cosθ     D．sinθ>tanθ> cosθ