九年级上二次函数知识点总结与练习
在一个等式中,只含有一个未知数,且未知数的最高次数是2次的整式方程叫做一元二次方程。
一元二次方程有四个特点:(1)只含有一个未知数;(2)且未知数次数最高次数是2;(3)是整式方程.要判断一个方程是否为一元二次方程,先看它是否为整式方程,若是,再对它进行整理.如果能整理为 ax^2+bx+c=0(a≠0)的形式,则这个方程就为一元二次方程. (4)将方程化为一般形式:ax^+bx+c=0时,应满足(a≠0)
22.2 降次——解一元二次方程
解一元二次方程的基本思想方法是通过“降次”将它化为两个一元一次方程。一元二次方程有四种解法:
1、直接开平方法:
用直接开平方法解形如(x-m)2=n (n≥0)的方程,其解为x=± m. 直接开平方法就是平方的逆运算.通常用根号表示其运算结果. 2、配方法
通过配成完全平方式的方法,得到一元二次方程的根的方法。这种解一元二次方程的方法称为配方法,配方的依据是完全平方公式。
1.转化: 将此一元二次方程化为ax^2+bx+c=0的形式(即一元二次方程的一般形式) 2.系数化1: 将二次项系数化为1 3.移项: 将常数项移到等号右侧
4.配方: 等号左右两边同时加上一次项系数一半的平方 5.变形: 将等号左边的代数式写成完全平方形式 6.开方: 左右同时开平方 7.求解: 整理即可得到原方程的根 3、公式法
公式法:把一元二次方程化成一般形式,然后计算判别式△=b2-4ac的值,当b2-4ac≥0时,把各项系数a, b, c的值代入求根公式x=(b2-4ac≥0)就可得到方程的根。
因式分解法:把方程变形为一边是零,把另一边的二次三项式分解成两个一次因式的积的形式,让两个一次因式分别等于零,得到两个一元一次方程,解这两个一元一次方程所得到的根,就是原方程的两个根。这种解一元二次方程的方法叫做因式分解法。
22.3 实际问题与一元二次方程
列一元二次方程解应用题是列一元一次方程解应用题的继续和发展
从列方程解应用题的方法来讲,列出一元二次方程解应用题与列出一元一次方程解应用题是非常相似的,由于一元一次方程未知数是一次,因此这类问题大部分都可通过算术方法来解决.如果未知数出现二次,用算术方法就很困难了,正由于未知数是二次的,所以可以用一元二次方程解决有关面积问题,经过两次增长的平均增长率问题,数学问题中涉及积的一些问题,经营决策问题等等
知识点一:二次函数的定义
1.二次函数的定义:
一般地,形如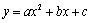 (
(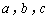 是常数,
是常数,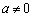 )的函数,叫做二次函数.
)的函数,叫做二次函数.
其中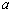 是二次项系数,
是二次项系数,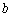 是一次项系数,
是一次项系数,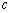 是常数项.
是常数项.
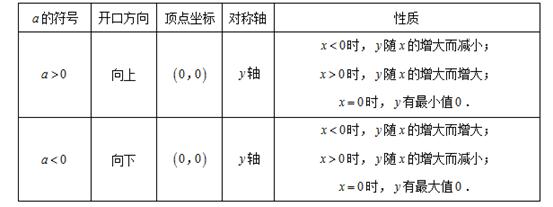
知识点二:二次函数的图象与性质 抛物线的三要素:开口、对称轴、顶点
抛物线的三要素:开口、对称轴、顶点
2. 二次函数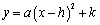 的图象与性质
的图象与性质
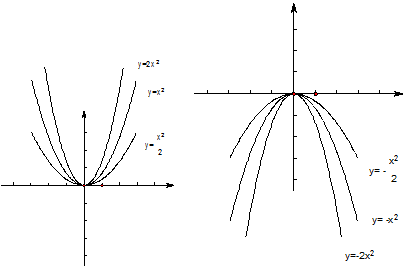
(1)二次函数基本形式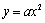 的图象与性质:a的绝对值越大,抛物线的开口越小
的图象与性质:a的绝对值越大,抛物线的开口越小
(2)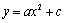 的图象与性质:上加下减
的图象与性质:上加下减

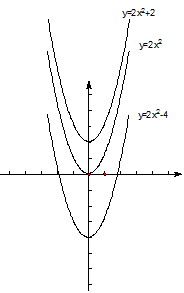
(3)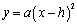 的图象与性质:左加右减
的图象与性质:左加右减


(4)二次函数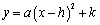 的图象与性质
的图象与性质
3. 二次函数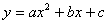 的图像与性质
的图像与性质
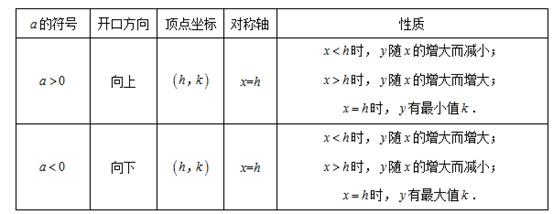
(1)当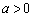 时,抛物线开口向上,对称轴为
时,抛物线开口向上,对称轴为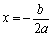 ,顶点坐标为
,顶点坐标为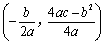 .
.
当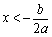 时,
时,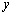 随
随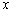 的增大而减小;当
的增大而减小;当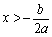 时,
时,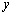 随
随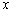 的增大而增大;当
的增大而增大;当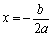 时,
时,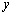 有最小值
有最小值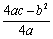 .
.
(2)当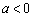 时,抛物线开口向下,对称轴为
时,抛物线开口向下,对称轴为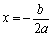 ,顶点坐标为
,顶点坐标为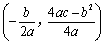 .
.
当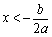 时,
时,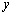 随
随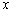 的增大而增大;当
的增大而增大;当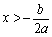 时,
时,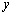 随
随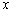 的增大而减小;当
的增大而减小;当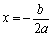 时,
时,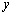 有最大值
有最大值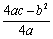 .
.
4. 二次函数常见方法指导
(1)二次函数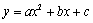 图象的画法
图象的画法
①画精确图 五点绘图法(列表-描点-连线)
利用配方法将二次函数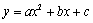 化为顶点式
化为顶点式 ,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.
,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.
②画草图 抓住以下几点:开口方向,对称轴,与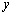 轴的交点,顶点.
轴的交点,顶点.
(2)二次函数图象的平移
平移步骤:
① 将抛物线解析式转化成顶点式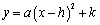 ,确定其顶点坐标
,确定其顶点坐标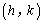 ;
;
② 可以由抛物线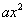 经过适当的平移得到具体平移方法如下:
经过适当的平移得到具体平移方法如下:
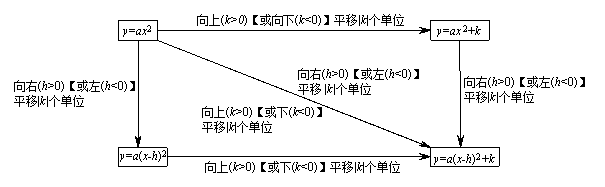
平移规律:概括成八个字“左加右减,上加下减”.
(3)用待定系数法求二次函数的解析式
①一般式: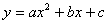 .已知图象上三点或三对
.已知图象上三点或三对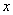 、
、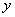 的值,通常选择一般式.
的值,通常选择一般式.
②顶点式: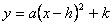 .已知图象的顶点或对称轴,通常选择顶点式.
.已知图象的顶点或对称轴,通常选择顶点式.
③交点式:  .已知图象与
.已知图象与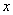 轴的交点坐标
轴的交点坐标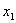 、
、 ,通常选择交点式.
,通常选择交点式.
(4)求抛物线的顶点、对称轴的方法
①公式法: ,∴顶点是
,∴顶点是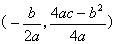 ,对称轴是直线
,对称轴是直线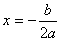 .
.
②配方法:运用配方的方法,将抛物线的解析式化为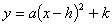 的形式,得到顶点为(
的形式,得到顶点为(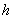 ,
,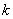 ),对称轴是直线
),对称轴是直线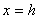 .
.
③运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.
(5)抛物线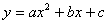 中,
中,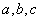 的作用
的作用
① 决定开口方向及开口大小,这与
决定开口方向及开口大小,这与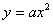 中的
中的 完全一样.
完全一样.
② 和
和 共同决定抛物线对称轴的位置
共同决定抛物线对称轴的位置
由于抛物线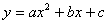 的对称轴是直线
的对称轴是直线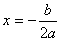 ,故
,故
如果 时,对称轴为
时,对称轴为 轴;
轴;
如果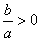 (即
(即 、
、 同号)时,对称轴在
同号)时,对称轴在 轴左侧;
轴左侧;
如果 (即
(即 、
、 异号)时,对称轴在
异号)时,对称轴在 轴右侧.
轴右侧.
③ 的大小决定抛物线
的大小决定抛物线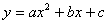 与
与 轴交点的位置
轴交点的位置
当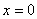 时,
时,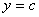 ,所以抛物线
,所以抛物线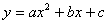 与
与 轴有且只有一个交点(0,
轴有且只有一个交点(0, ),故
),故
如果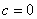 ,抛物线经过原点;
,抛物线经过原点;
如果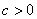 ,与
,与 轴交于正半轴;
轴交于正半轴;
如果 ,与
,与 轴交于负半轴.
轴交于负半轴.
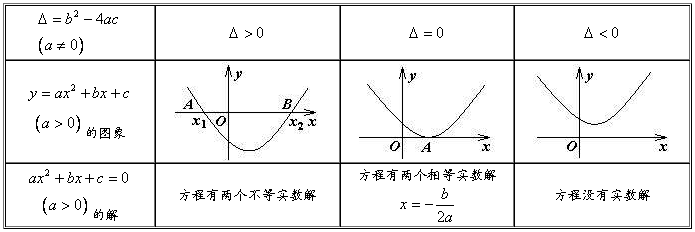
知识点三:二次函数与一元二次方程的关系
5.函数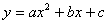 ,当
,当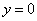 时,得到一元二次方程
时,得到一元二次方程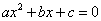 ,那么一元二次方程的解就是二次函数的图象与
,那么一元二次方程的解就是二次函数的图象与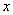 轴交点的横坐标,因此二次函数图象与
轴交点的横坐标,因此二次函数图象与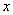 轴的交点情况决定一元二次方程根的情况.
轴的交点情况决定一元二次方程根的情况.
(1)当二次函数的图象与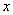 轴有两个交点,这时
轴有两个交点,这时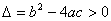 ,则方程有两个不相等实根;
,则方程有两个不相等实根;
(2)当二次函数的图象与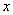 轴有且只有一个交点,这时
轴有且只有一个交点,这时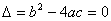 ,则方程有两个相等实根;(3)当二次函数的图象与
,则方程有两个相等实根;(3)当二次函数的图象与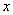 轴没有交点,这时
轴没有交点,这时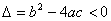 ,则方程没有实根.
,则方程没有实根.
通过下面表格可以直观地观察到二次函数图象和一元二次方程的关系:
6.拓展:关于直线与抛物线的交点知识
(1) 轴与抛物线
轴与抛物线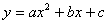 得交点为
得交点为 .
.
(2)与 轴平行的直线
轴平行的直线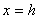 与抛物线
与抛物线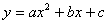 有且只有一个交点(
有且只有一个交点(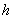 ,
,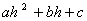 ).
).
(3)抛物线与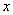 轴的交点
轴的交点
二次函数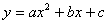 的图像与
的图像与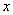 轴的两个交点的横坐标
轴的两个交点的横坐标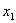 、
、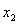 ,是对应一元二次方程
,是对应一元二次方程 的两个实数根.抛物线与
的两个实数根.抛物线与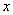 轴的交点情况可以由对应的一元二次方程的根的判别式判定:
轴的交点情况可以由对应的一元二次方程的根的判别式判定:
①有两个交点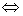
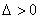
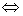 抛物线与
抛物线与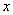 轴相交;
轴相交;
②有一个交点(顶点在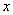 轴上)
轴上)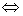
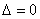
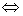 抛物线与
抛物线与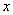 轴相切;
轴相切;
③没有交点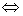
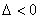
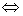 抛物线与
抛物线与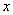 轴相离.
轴相离.
(4)平行于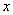 轴的直线与抛物线的交点
轴的直线与抛物线的交点
同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为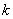 ,则横坐标是
,则横坐标是 的两个实数根.
的两个实数根.
(5)一次函数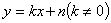 的图像
的图像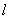 与二次函数
与二次函数 的图像
的图像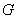 的交点,由方程组
的交点,由方程组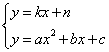 的解的数目来确定:
的解的数目来确定:
①方程组有两组不同的解时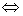
 与
与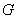 有两个交点;
有两个交点;
②方程组只有一组解时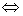
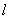 与
与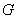 只有一个交点;
只有一个交点;
③方程组无解时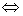
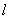 与
与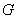 没有交点.
没有交点.
(6)抛物线与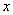 轴两交点之间的距离:若抛物线
轴两交点之间的距离:若抛物线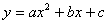 与
与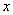 轴两交点为
轴两交点为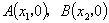 ,由于
,由于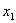 、
、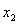 是方程
是方程 的两个根,故
的两个根,故
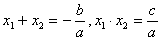
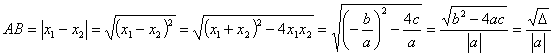
知识点四:利用二次函数解决实际问题
7.利用二次函数解决实际问题,要建立数学模型,即把实际问题转化为二次函数问题,利用题中存在的公式、内含的规律等相等关系,建立函数关系式,再利用函数的图象及性质去研究问题.在研究实际问题时要注意自变量的取值范围应具有实际意义.
利用二次函数解决实际问题的一般步骤是:
(1)建立适当的平面直角坐标系;
(2)把实际问题中的一些数据与点的坐标联系起来;
(3)用待定系数法求出抛物线的关系式;
(4)利用二次函数的图象及其性质去分析问题、解决问题.
第二篇:二次函数小结与思考
二次函数(复习)
知识结构:
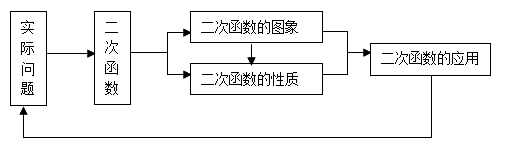
知识点:
一、二次函数概念:形如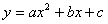 (a≠0,a,b,c为常数)的函数叫x的二次函数。
(a≠0,a,b,c为常数)的函数叫x的二次函数。
二、二次函数的图象关系:



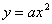 (a≠0)
(a≠0) 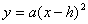 (a≠0,a,h为常数)
(a≠0,a,h为常数)

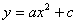 ( a≠0,a,k为常数)
( a≠0,a,k为常数)  +k(a≠0,a,h,k为常数)三、二次函数的特性:(填表)
+k(a≠0,a,h,k为常数)三、二次函数的特性:(填表)

四、实践与探索
巩固练习:
①二次函数的定义:
(1).下列函数中,二次函数的是( )
A.y=ax2+bx+c B。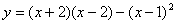 C。
C。 D。y=x(x—1)
D。y=x(x—1)
⑵.当k= 时,函数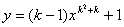 为二次函数。
为二次函数。
②二次函数的图像与性质:
二次函数y=-x2+6x+3的图象开口方向 顶点坐标为____ _____对称轴为_________
当x= 时函数有 值,为 。当x 时,y的值随x的增大而增大。它是由y=-x2向 平移 个单位得到的,再向 平移 个单位得到的.
 ③抛物线
③抛物线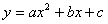 与x轴的交点个数:
与x轴的交点个数:
抛物线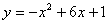 与x轴的交点有 个,抛物线
与x轴的交点有 个,抛物线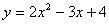 与x轴的交点有 个,抛物线y=x2+2x+1与x轴的交点有 个。
与x轴的交点有 个,抛物线y=x2+2x+1与x轴的交点有 个。
总结:抛物线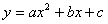 与x轴的交点个数由 决定。
与x轴的交点个数由 决定。
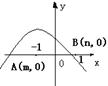 ④抛物线
④抛物线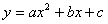 的图象与a、b、c及b2-4ac的关系。
的图象与a、b、c及b2-4ac的关系。
⑴如图是y=ax2+bx+c的图象,则a______0 b______0
c______0 b2-4ac________0
⑵.二次函数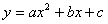 与一次函数
与一次函数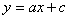 在同一直角坐标系中图象大致是 ( )
在同一直角坐标系中图象大致是 ( )

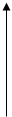
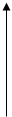
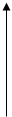
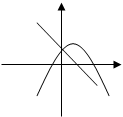









A B C D
(3).函数 的图象与
的图象与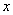 轴有交点,则
轴有交点,则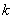 的取值范围是( )
的取值范围是( )
A.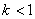 B.
B.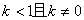 C.
C. D.
D.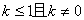
总结:抛物线 的图象与a、b、c及b2-4ac的关系是:
的图象与a、b、c及b2-4ac的关系是:
a:开口方向;b:结合a看对称轴;c:与y轴交点坐标;b2-4ac:与x轴的交点个数。
⑤求函数解析式:
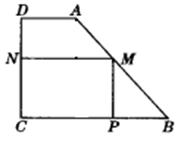
例1.如图,有一块形状是直角梯形的铁皮ABCD,它的上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm.现要裁成一块矩形铁皮MPCN,使它的顶点M、P、N分别在AB、BC、CD上.当MN是多长时,矩形MPCN的面积有最大值?
例2:探索:如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于C点,点A、C的坐标分别是(-1,0)(0,1.5)
(1)求此抛物线的函数关系式。
(2)若点P是此抛物线上位于x轴上方的一个动点,求三角形ABP面积的最大值。
(3)问:此抛物线位于x轴的下方是否存在一点Q,,使△ABQ的面积与△ABP的面积相等?如果有,求出该点坐标,如果没有请说明理由。
-
初中数学二次函数知识点总结
初中数学二次函数知识点总结原文阅读I.定义与定义表达式一般地,自变量x和因变量y之间存在如下关系:y=ax^2+bx+c(a,b,…
-
中学数学二次函数知识点总结教案
二次函数知识点总结二次函数知识点:1.二次函数的概念:一般地,形如y?ax2?bx?c(a、b、c是常数,a?0)的函数,叫做二次…
-
二次函数知识点总结(9下)
东营小学至高三文化课辅导专业机构西城:8278520二次函数的性质二次函数的最值:东营小学至高三文化课辅导专业机构西城:82785…
-
二次函数知识点总结——题型分类总结
二次函数知识点总结——题型分类总结一、二次函数的定义(考点:二次函数的二次项系数不为0,且二次函数的表达式必须为整式)1、下列函数…
-
二次函数知识点 总结
一元二次函数知识点总结1.定义:一般地,如果y?ax2?bx?c(a,b,c是常数,a?0),那么y叫做x的一元二次函数.2.二次…
-
初三二次函数总结版
授课时间5月26日授课地点东岗路年级初三课型一对一上课人数1课题二次函数概念性质对称平移图像教学目标1掌握二次函数的概念及其考察方…
-
初三数学二次函数知识点总结
初三数学二次函数知识点总结一二次函数概念1二次函数的概念一般地形如yax2bxca的函数叫做二次函数这bc是常数a0里需要强调和一…
-
初中函数总结含表格
骄阳学堂初中函数知识点总结一直角坐标系1点到坐标轴及原点的距离点Pxy到坐标轴及原点的距离1到x轴的距离等于y2到y轴的距离等于x…
-
二次函数图表总结
yaxk上下平移yaxh2k上下平移yaxh22一般地抛物线yaxhk与yax2的形状相同位置不同向右hgt0或左h平移k个单位或…
- 九年级二次函数知识点复习表格