二次函数的图象和性质总结

(一)y=a(x-h)²+k(a¹0)的图象和性质

                   

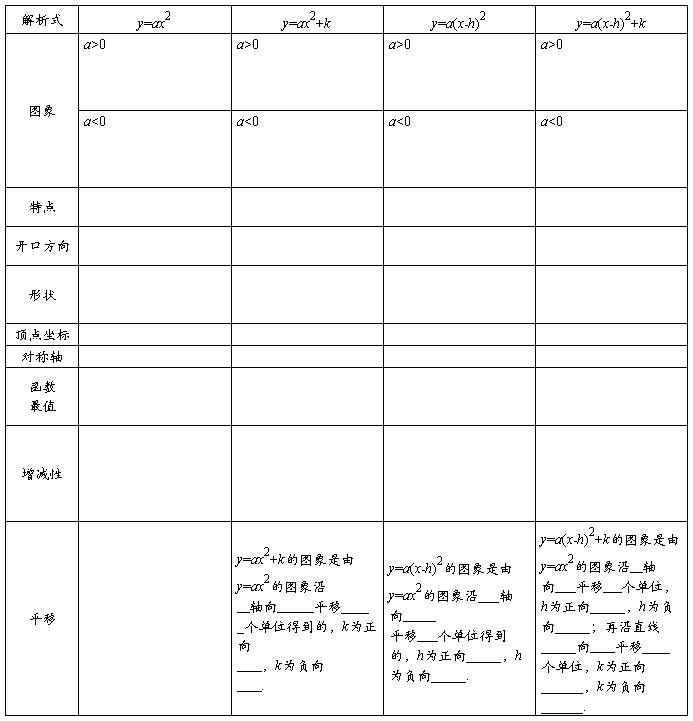
二次函数的图象和性质总结

    (一) 二次函数的图象与性质

                                                                     

(二) a、b、c的符号对抛物线形状位置的影响

(三) 解析式

 

第二篇：初二数学一次函数_一次函数知识点总结_初二数学一次函数复习

一次函数知识点总结

基本概念：

1、 变量：在一个变化过程中可以取不同数值的量。 常量：在一个变化过程中只能取同一数值的量。

2、函数：一般的，在一个变化过程中，如果有两个变量x和y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就把x称为自变量，把y称为因变量，y是x的函数。 3、定义域：一般的，一个函数的自变量允许取值的范围，叫做这个函数的定义域。

4、确定函数定义域的方法：

（1）关系式为整式时，函数定义域为全体实数； （2）关系式含有分式时，分式的分母不等于零； （3）关系式含有二次根式时，被开放方数大于等于零； （4）关系式中含有指数为零的式子时，底数不等于零； （5）实际问题中，函数定义域还要和实际情况相符合，使之有意义。 函数性质：

1.y的变化值与对应的x的变化值成正比例，比值为k. 即：y=kx+b（k，b为常数，k≠0）。

2.当x=0时，b为函数在y轴上的点,坐标为(0，b)。

3当b=0时(即 y=kx)，一次函数图像变为正比例函数，正比例函数是特殊的一次函数。

4.在两个一次函数表达式中：

当两一次函数表达式中的k相同，b也相同时，两一次函数图像重合；

当两一次函数表达式中的k相同，b不相同时，两一次函数图像平行；

当两一次函数表达式中的k不相同，b不相同时，两一次函数图像相交；

当两一次函数表达式中的k不相同，b相同时，两一次函数图像交于y轴上的同一点（0，b）。 图像性质

1．作法与图形： （1）列表.

（2）描点；一般取两个点,根据“两点确定一条直线”的道理，也可叫“两点法”。 一般的y=kx+b(k≠0）的图象过（0，b）和（-b/k，0）两点画直线即可。

正比例函数y=kx(k≠0）的图象是过坐标原点的一条直线，一般取（0,0）和（1，k）两点。 2．性质：

（1）在一次函数上的任意一点P（x，y），都满足等式：y=kx+b(k≠0)。

（2）一次函数与y轴交点的坐标总是（0，b)，与x轴总是交于（-b/k，0）正比例函数的图像都是过原点。

3．函数不是数，它是指某一变化过程中两个变量之间的关系。

一次函数的图象特征和性质：

4、特殊位置关系：

当平面直角坐标系中两直线平行时，其函数解析式中K值（即一次项系数）相等

当平面直角坐标系中两直线垂直时，其函数解析式中K值互为负倒数（即两个K值的乘积为-1） 了解 如何设一次函数解析式：

点斜式 y-y1=k(x-x1)（k为直线斜率,(x1,y1)为该直线所过的一个点）

两点式 (y-y1) / (y2-y1)=(x-x1)/(x2-x1)（已知直线上（x1,y1）与（x2,y2）两点）

截距式 （y=-b/ax+b a、b分别为直线在x、y轴上的截距 ,已知（0，b）,(a，0) ） 实用型 （由实际问题来做） 扩展

1. 求函数图像的

k值：(y1-y2)/(x1-x2)

2.求任意线段的长：√(x1-x2) 2+(y1-y2) 2

3.求两个一次函数式图像交点坐标：解两函数式,就是解方程组 4.求任意2点所连线段的中点坐标：[（x1+x2）/2，（y1+y2）/2 ] 5.若两条直线y1=k1x+b1平行y2=k2x+b2，那么k1=k2，b1≠b2 6 . 向右平移n个单位 y=k（x-n）+b 向左平移n个单位 y=k（x+n）+b 向上平移n个单位 y =kx+b+n

向下平移n个单位 y =kx+b-n

总结与前几章的关系

1、一元一次方程与一次函数的关系

任何一元一次方程到可以转化为ax+b=0（a，b为常数，a≠0）的形式，所以解一元一次方程可以转化为：当某个一次函数的值为0时，求相应的自变量的值. 从图象上看，相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值. 2、一次函数与一元一次不等式的关系

任何一个一元一次不等式都可以转化为ax+b>0或ax+b<0（a，b为常数，a≠0）的形式，所以解一元一次不等式可以看作：当一次函数值大（小）于0时，求自变量的取值范围. 3、一次函数与二元一次方程组

（1）以二元一次方程ax+by=c的解为坐标的点组成的图象与一次函数y=?x?的图象相同.

（2）二元一次方程组的解可以看作是两个一次函数和的图象交点.

ab

cb

深本数学，总结了中小学数学四个大规律，十五个中规律和三十五个小规律