高中数学人教版选修2-2导数及其应用知识点总结
数学选修2-2导数及其应用知识点必记
1.函数的平均变化率为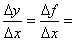
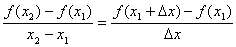
注1:其中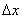 是自变量的改变量,可正,可负,可零。
是自变量的改变量,可正,可负,可零。
注2:函数的平均变化率可以看作是物体运动的平均速度。
2、导函数的概念:函数 在
在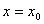 处的瞬时变化率是
处的瞬时变化率是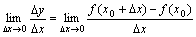 ,则称函数
,则称函数 在点
在点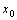 处可导,并把这个极限叫做
处可导,并把这个极限叫做 在
在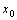 处的导数,记作
处的导数,记作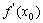 或
或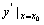 ,即
,即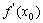 =
=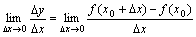 .
.
3.函数的平均变化率的几何意义是割线的斜率;函数的导数的几何意义是切线的斜率。
4导数的背景(1)切线的斜率;(2)瞬时速度;(3)边际成本。
5、常见的函数导数和积分公式

6、常见的导数和定积分运算公式:若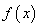 ,
,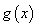 均可导(可积),则有:
均可导(可积),则有:

6.用导数求函数单调区间的步骤:①求函数f(x)的导数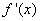 ②令
②令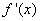 >0,解不等式,得x的范围就是递增区间.③令
>0,解不等式,得x的范围就是递增区间.③令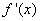 <0,解不等式,得x的范围,就是递减区间;[注]:求单调区间之前一定要先看原函数的定义域。
<0,解不等式,得x的范围,就是递减区间;[注]:求单调区间之前一定要先看原函数的定义域。
7.求可导函数f(x)的极值的步骤:(1)确定函数的定义域。(2) 求函数f(x)的导数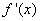 (3)求方程
(3)求方程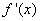 =0的根(4) 用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格,检查
=0的根(4) 用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格,检查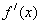 在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号,那么f(x)在这个根处无极值
在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号,那么f(x)在这个根处无极值
8.利用导数求函数的最值的步骤:求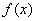 在
在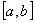 上的最大值与最小值的步骤如下: ⑴求
上的最大值与最小值的步骤如下: ⑴求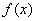 在
在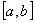 上的极值;⑵将
上的极值;⑵将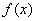 的各极值与
的各极值与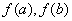 比较,其中最大的一个是最大值,最小的一个是最小值。[注]:实际问题的开区间唯一极值点就是所求的最值点;
比较,其中最大的一个是最大值,最小的一个是最小值。[注]:实际问题的开区间唯一极值点就是所求的最值点;
9.求曲边梯形的思想和步骤:分割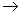 近似代替
近似代替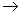 求和
求和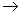 取极限 (“以直代曲”的思想)
取极限 (“以直代曲”的思想)
10.定积分的性质
根据定积分的定义,不难得出定积分的如下性质:
性质1 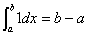
性质5 若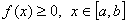 ,则
,则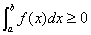
①推广: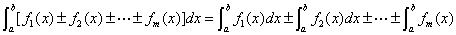
②推广: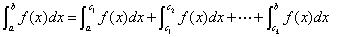
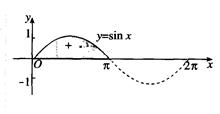 11定积分的取值情况:定积分的值可能取正值,也可能取负值,还可能是0.
11定积分的取值情况:定积分的值可能取正值,也可能取负值,还可能是0.
( l )当对应的曲边梯形位于 x 轴上方时,定积分的值取正值,且等于x轴上方的图形面积;
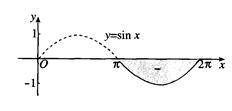 (2)当对应的曲边梯形位于 x 轴下方时,定积分的值取负值,且等于x轴上方图形面积的相反数;
(2)当对应的曲边梯形位于 x 轴下方时,定积分的值取负值,且等于x轴上方图形面积的相反数;
(3)当位于 x 轴上方的曲边梯形面积等于位于 x 轴下方的曲边梯形面积时,定积分的值为0,且等于x轴上方图形的面积减去下方的图形的面积.
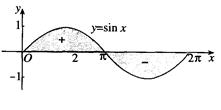
12.物理中常用的微积分知识(1)位移的导数为速度,速度的导数为加速度。(2)力的积分为功。
推理与证明知识点
13.归纳推理的定义:从个别事实中推演出一般性的结论,像这样的推理通常称为归纳推理。
归纳推理是由部分到整体,由个别到一般的推理。
14.归纳推理的思维过程
大致如图: 
15.归纳推理的特点: ①归纳推理的前提是几个已知的特殊现象,归纳所得的结论是尚属未知的一般现象。②由归纳推理得到的结论具有猜测的性质,结论是否真实,还需经过逻辑证明和实验检验,因此,它不能作为数学证明的工具。③归纳推理是一种具有创造性的推理,通过归纳推理的猜想,可以作为进一步研究的起点,帮助人们发现问题和提出问题。
16.类比推理的定义:根据两个(或两类)对象之间在某些方面的相似或相同,推演出它们在其他方面也相似或相同,这样的推理称为类比推理。类比推理是由特殊到特殊的推理。
17.类比推理的思维过程

18.演绎推理的定义:演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等)按照严格的逻辑法则得到新结论的推理过程。演绎推理是由一般到特殊的推理。
19.演绎推理的主要形式:三段论
20.“三段论”可以表示为:①大前题:M是P②小前提:S是M ③结论:S是P。
其中①是大前提,它提供了一个一般性的原理;②是小前提,它指出了一个特殊对象;③是结论,它是根据一般性原理,对特殊情况做出的判断。
21.直接证明是从命题的条件或结论出发,根据已知的定义、公理、定理,直接推证结论的真实性。直接证明包括综合法和分析法。
22.综合法就是“由因导果”,从已知条件出发,不断用必要条件代替前面的条件,直至推出要证的结论。
23.分析法就是从所要证明的结论出发,不断地用充分条件替换前面的条件或者一定成立的式子,可称为“由果索因”。要注意叙述的形式:要证A,只要证B,B应是A成立的充分条件. 分析法和综合法常结合使用,不要将它们割裂开。
24反证法:是指从否定的结论出发,经过逻辑推理,导出矛盾,证实结论的否定是错误的,从而肯定原结论是正确的证明方法。
25.反证法的一般步骤(1)假设命题结论不成立,即假设结论的反面成立; (2)从假设出发,经过推理论证,得出矛盾;(3)从矛盾判定假设不正确,即所求证命题正确。
26常见的“结论词”与“反义词”

27.反证法的思维方法:正难则反
28.归缪矛盾(1)与已知条件矛盾:(2)与已有公理、定理、定义矛盾; (3)自相矛盾.
29.数学归纳法(只能证明与正整数有关的数学命题)的步骤(1)证明:当n取第一个值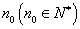 时命题成立;(2)假设当n=k (k∈N*,且k≥n0)时命题成立,证明当n=k+1时命题也成立.由(1),(2)可知,命题对于从n0开始的所有正整数n都正确
时命题成立;(2)假设当n=k (k∈N*,且k≥n0)时命题成立,证明当n=k+1时命题也成立.由(1),(2)可知,命题对于从n0开始的所有正整数n都正确  [注]:常用于证明不完全归纳法推测所得命题的正确性的证明。
[注]:常用于证明不完全归纳法推测所得命题的正确性的证明。
数系的扩充和复数的概念知识点
30.复数的概念:形如a+bi的数叫做复数,其中i叫虚数单位,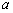 叫实部,
叫实部, 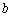 叫虚部,数集
叫虚部,数集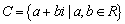 叫做复数集。
叫做复数集。
规定: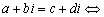 a=c且b=d,强调:两复数不能比较大小,只有相等或不相等。
a=c且b=d,强调:两复数不能比较大小,只有相等或不相等。
31.数集的关系: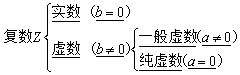
32.复数的几何意义:复数与平面内的点或有序实数对一一对应。
33.复平面:根据复数相等的定义,任何一个复数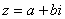 ,都可以由一个有序实数对
,都可以由一个有序实数对 唯一确定。由于有序实数对
唯一确定。由于有序实数对 与平面直角坐标系中的点一一对应,因此复数集与平面直角坐标系中的点集之间可以建立一一对应。这个建立了直角坐标系来表示复数的平面叫做复平面,
与平面直角坐标系中的点一一对应,因此复数集与平面直角坐标系中的点集之间可以建立一一对应。这个建立了直角坐标系来表示复数的平面叫做复平面,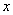 轴叫做实轴,
轴叫做实轴, 轴叫做虚轴。实轴上的点都表示实数,除了原点外,虚轴上的点都表示纯虚数。
轴叫做虚轴。实轴上的点都表示实数,除了原点外,虚轴上的点都表示纯虚数。
34.求复数的模(绝对值)与复数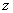 对应的向量
对应的向量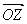 的模
的模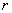 叫做复数
叫做复数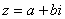 的模(也叫绝对值)记作
的模(也叫绝对值)记作 。由模的定义可知:
。由模的定义可知: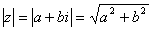
35.复数的加、减法运算及几何意义①复数的加、减法法则: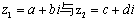 ,则
,则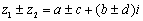 。注:复数的加、减法运算也可以按向量的加、减法来进行。
。注:复数的加、减法运算也可以按向量的加、减法来进行。
②复数的乘法法则: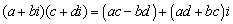 。
。
③复数的除法法则: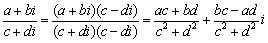 其中
其中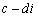 叫做实数化因子
叫做实数化因子
36.共轭复数:两复数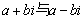 互为共轭复数,当
互为共轭复数,当 时,它们叫做共轭虚数。
时,它们叫做共轭虚数。
常见的运算规律
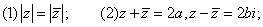
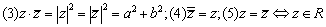
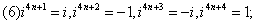
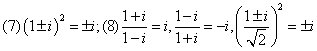
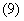 设
设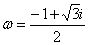 是1的立方虚根,则
是1的立方虚根,则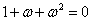 ,
,
第二篇:高二数学导数及其应用复习讲义有答案
高二数学复习讲义—导数及其应用
知识归纳
1.导数的概念
函数y=f(x),如果自变量x在x 处有增量
处有增量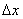 ,那么函数y相应地有增量
,那么函数y相应地有增量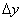 =f(x
=f(x +
+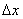 )-f(x
)-f(x ),比值
),比值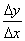 叫做函数y=f(x)在x
叫做函数y=f(x)在x 到x
到x +
+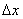 之间的平均变化率,即
之间的平均变化率,即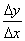 =
=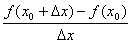 。如果当
。如果当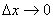 时,
时,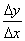 有极限,我们就说函数y=f(x)在点x
有极限,我们就说函数y=f(x)在点x 处可导,并把这个极限叫做f(x)在点x
处可导,并把这个极限叫做f(x)在点x 处的导数,记作f’(x
处的导数,记作f’(x )或y’|
)或y’|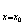 。
。
即f(x )=
)=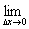
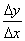 =
=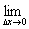
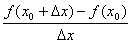 。
。
说明:(1)函数f(x)在点x 处可导,是指
处可导,是指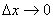 时,
时,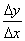 有极限。如果
有极限。如果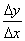 不存在极限,就说函数在点x
不存在极限,就说函数在点x 处不可导,或说无导数。
处不可导,或说无导数。
(2)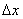 是自变量x在x
是自变量x在x 处的改变量,
处的改变量, 时,而
时,而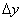 是函数值的改变量,可以是零。
是函数值的改变量,可以是零。
由导数的定义可知,求函数y=f(x)在点x 处的导数的步骤:
处的导数的步骤:
(1)求函数的增量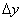 =f(x
=f(x +
+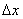 )-f(x
)-f(x );
);
(2)求平均变化率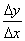 =
=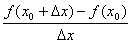 ;
;
(3)取极限,得导数f’(x )=
)=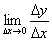 。
。
2.导数的几何意义
函数y=f(x)在点x 处的导数的几何意义是曲线y=f(x)在点p(x
处的导数的几何意义是曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率。也就是说,曲线y=f(x)在点p(x
))处的切线的斜率。也就是说,曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率是f’(x
))处的切线的斜率是f’(x )。相应地,切线方程为y-y
)。相应地,切线方程为y-y =f/(x
=f/(x )(x-x
)(x-x )。
)。
3.几种常见函数的导数:
① ②
② ③
③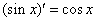 ; ④
; ④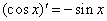 ;
;
⑤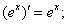 ⑥
⑥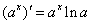 ;
;
⑦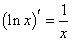 ; ⑧
; ⑧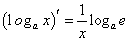 .
.
4.两个函数的和、差、积的求导法则
法则1:两个函数的和(或差)的导数,等于这两个函数的导数的和(或差),
即: (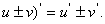
法则2:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个
函数乘以第二个函数的导数,即: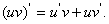
若C为常数,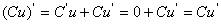 .即常数与函数的积的导数等于常数乘以函数的导数:
.即常数与函数的积的导数等于常数乘以函数的导数: 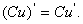
法则3:两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积再除以分母的平方: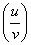 ‘=
‘=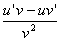 (v
(v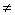 0)。
0)。
形如y=f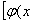
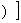 的函数称为复合函数。复合函数求导步骤:分解——求导——回代。法则:y'|
的函数称为复合函数。复合函数求导步骤:分解——求导——回代。法则:y'|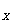 = y'|
= y'|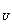 ·u'|
·u'|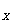
5.单调区间:一般地,设函数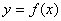 在某个区间可导,
在某个区间可导,
如果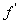
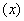
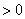 ,则
,则 为增函数;
为增函数;
如果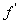
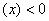 ,则
,则 为减函数;
为减函数;
如果在某区间内恒有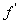
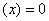 ,则
,则 为常数;
为常数;
6.极点与极值:
曲线在极值点处切线的斜率为0,极值点处的导数为0;曲线在极大值点左侧切线的斜率为正,右侧为负;曲线在极小值点左侧切线的斜率为负,右侧为正;
7.最值:
一般地,在区间[a,b]上连续的函数f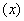 在[a,b]上必有最大值与最小值。
在[a,b]上必有最大值与最小值。
①求函数?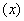 在(a,b)内的极值;
在(a,b)内的极值;
②求函数?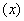 在区间端点的值?(a)、?(b);
在区间端点的值?(a)、?(b);
③将函数? 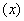 的各极值与?(a)、?(b)比较,其中最大的是最大值,其中最小的是最小值。
的各极值与?(a)、?(b)比较,其中最大的是最大值,其中最小的是最小值。
高考题型
1.导数定义的应用
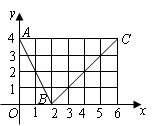 例1 (北京高考)如图,函数
例1 (北京高考)如图,函数 的图象是折线段
的图象是折线段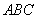 ,其中
,其中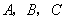 的坐标分别为
的坐标分别为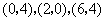 ,
, 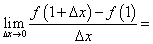 _________.
_________.
解:由图可知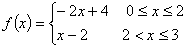 ,根据导数的定义
,根据导数的定义
知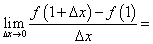
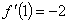 .
.
例2(重庆高考)已知函数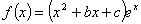 ,其中
,其中 ,(Ⅰ)略,(Ⅱ)若
,(Ⅰ)略,(Ⅱ)若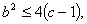 且
且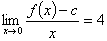 ,试证:
,试证: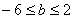 .
.
解: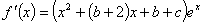 ,易知
,易知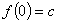 .故
.故
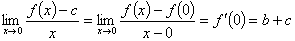 ,
,
所以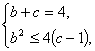 解得
解得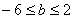 .
.
2. 利用导数研究函数的图像
例3 (安徽高考)设 <b,函数
<b,函数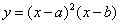 的图像可能是
的图像可能是
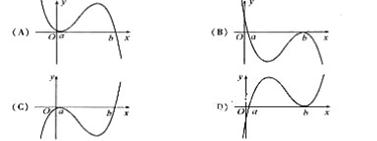
解: ,由
,由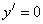 得
得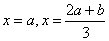 ,∴当
,∴当 时,
时,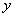 取极大值0,当
取极大值0,当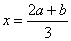 时
时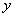 取极小值且极小值为负.故选C.或当
取极小值且极小值为负.故选C.或当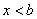 时
时 ,当
,当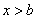 时,
时,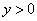 选C.
选C.
点评:通过导数研究函数图像的变化规律,也是考试的热点题型.
3.利用导数解决函数的单调性问题
例5(全国高考)已知函数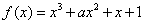 ,
, .
.
(Ⅰ)讨论函数 的单调区间;
的单调区间;
(Ⅱ)设函数 在区间
在区间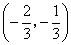 内是减函数,求
内是减函数,求 的取值范围.
的取值范围.
解:(1)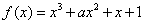 求导得
求导得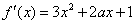
当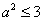 时,
时,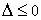 ,
,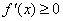 ,
, 在
在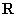 上递增;
上递增;
当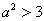 ,
,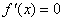 求得两根为
求得两根为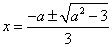 ,
,
即 在
在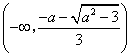 递增,
递增,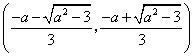 递减,
递减, 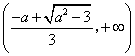 递增。
递增。
(2)因为函数 在区间
在区间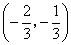 内是减函数,所以当
内是减函数,所以当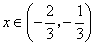 时
时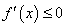 恒成立,结合二次函数的图像可知
恒成立,结合二次函数的图像可知 解得
解得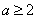 .
.
点评:函数在某区间上单调转化为导函数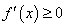 或
或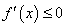 在区间上恒成立问题,是解决这类问题的通法.本题也可以由函数在
在区间上恒成立问题,是解决这类问题的通法.本题也可以由函数在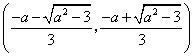 上递减,所以
上递减,所以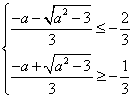 求解.
求解.
【变式1】( 全国高考)若函数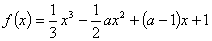 在区间
在区间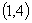 上是减函数,在区间
上是减函数,在区间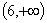 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
解: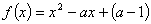 ,令
,令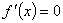 得
得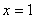 或
或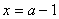 ,结合图像知
,结合图像知 ,故
,故 .
.
点评:本题也可转化为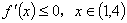 恒成立且
恒成立且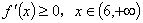 恒成立来解.
恒成立来解.
【变式2】( 浙江高考)已知函数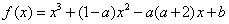
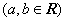 .若函数
.若函数 在区间
在区间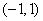 上不单调,求
上不单调,求 的取值范围.
的取值范围.
解:函数 在区间
在区间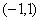 不单调,等价于
不单调,等价于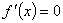 在区间
在区间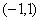 上有实数解,且无重根.
上有实数解,且无重根.
又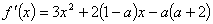 ,由
,由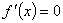 ,得
,得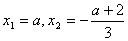 。从而
。从而
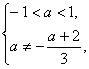 或
或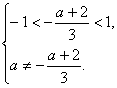 解得
解得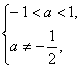 或
或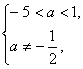
所以 的取值范围是
的取值范围是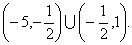
点评:这种逆向设问方式是今后高考命题的一种趋势,充分体现高考“能力立意”的思想,高考中应高度重视。
(4)利用导数的几何意义研究曲线的切线问题
例6 (江西高考)若存在过点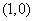 的直线与曲线
的直线与曲线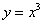 和
和 都相切,则
都相切,则 等于
等于
A.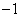 或
或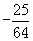 B.
B.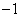 或
或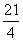 C.
C.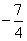 或
或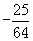 D.
D.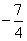 或
或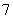
解:设过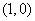 的直线与
的直线与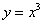 相切于点
相切于点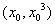 ,所以切线方程为
,所以切线方程为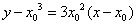
即 ,又
,又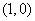 在切线上,则
在切线上,则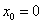 或
或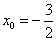 ,
,
当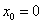 时,由
时,由 与
与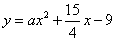 相切可得
相切可得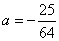 ,
,
当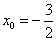 时,由
时,由 与
与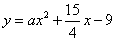 相切可得
相切可得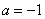 ,所以选
,所以选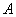 .
.
点评:函数的切线问题,切点是关键,因为它是联结曲线和其切线的“桥梁”,在做题中往往需要设出切点.
【变式】( 辽宁高考)设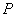 为曲线
为曲线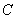 :
: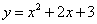 上的点,且曲线
上的点,且曲线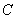 在点
在点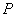 处切线倾斜角的取值范围为
处切线倾斜角的取值范围为 ,则点
,则点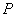 横坐标的取值范围为( )
横坐标的取值范围为( )
A.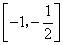 B.
B.
C.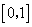 D.
D.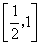
解:由曲线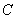 在点
在点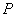 处切线倾斜角的取值范围为
处切线倾斜角的取值范围为 ,可得曲线
,可得曲线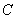 在点
在点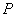 处切线的斜率范围为
处切线的斜率范围为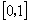 ,又
,又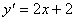 ,设点
,设点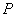 的横坐标为
的横坐标为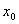 ,则
,则 ,解得
,解得 ,故选
,故选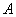 .
.
5. 利用导数求函数的极值与最值
例7(天津高考)已知函数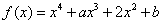 (
(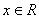 ),其中
),其中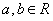 .若函数
.若函数 仅在
仅在 处有极值,求
处有极值,求 的取值范围.
的取值范围.
解: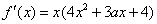 ,显然
,显然 不是方程
不是方程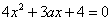 的根.
的根.
为使 仅在
仅在 处有极值,必须
处有极值,必须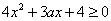 成立,即有
成立,即有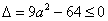 .
.
解不等式,得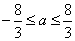 .这时,
.这时,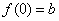 是唯一极值.因此满足条件的
是唯一极值.因此满足条件的 的取值范围是
的取值范围是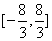 .
.
6.利用导数解决实际问题
例8用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
解:设长方体的宽为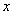 (m),则长为
(m),则长为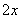 (m),高为
(m),高为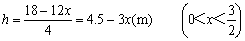 .
.
故长方体的体积为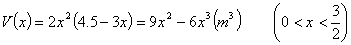
从而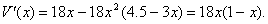 令
令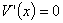 ,解得
,解得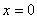 (舍去)或
(舍去)或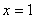 ,因此
,因此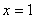 .
.
当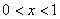 时,
时,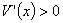 ;当
;当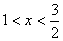 时,
时,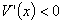 ,故在
,故在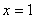 处
处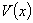 取得极大值,并且这个极大值就是
取得极大值,并且这个极大值就是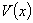 的最大值,从而最大体积
的最大值,从而最大体积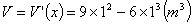 ,此时长方体的长为2 m,高为1.5 m
,此时长方体的长为2 m,高为1.5 m
导数及其应用 [基础训练A组]
一、选择题
1.若函数 在区间
在区间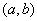 内可导,且
内可导,且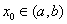 则
则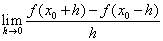
的值为( B )
A.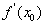 B.
B.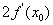 C.
C. D.
D.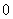
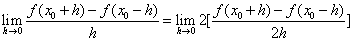
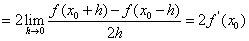
2.一个物体的运动方程为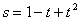 其中
其中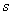 的单位是米,
的单位是米,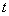 的单位是秒,
的单位是秒,
那么物体在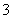 秒末的瞬时速度是(C )
秒末的瞬时速度是(C )
A.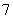 米/秒 B.
米/秒 B.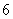 米/秒
米/秒
C.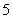 米/秒 D.
米/秒 D.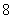 米/秒
米/秒
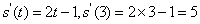
3.函数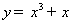 的递增区间是(C )
的递增区间是(C )
A.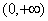 B.
B.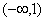
C.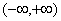 D.
D.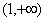
 对于任何实数都恒成立
对于任何实数都恒成立
4.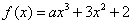 ,若
,若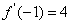 ,则
,则 的值等于(D )
的值等于(D )
A. B.
B.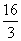
C.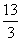 D.
D.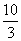
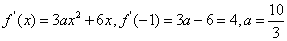
5.函数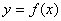 在一点的导数值为
在一点的导数值为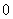 是函数
是函数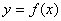 在这点取极值的( D )
在这点取极值的( D )
A.充分条件 B.必要条件
C.充要条件 D.必要非充分条件
对于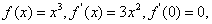 不能推出
不能推出 在
在 取极值,反之成立
取极值,反之成立
6.函数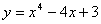 在区间
在区间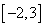 上的最小值为(D )
上的最小值为(D )
A.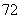 B.
B. C.
C.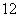 D.
D.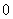
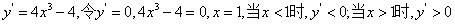
得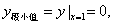 而端点的函数值
而端点的函数值 ,得
,得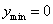
二、填空题
1.若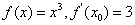 ,则
,则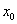 的值为_______
的值为_______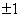 __________;
__________;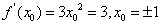
2.曲线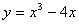 在点
在点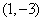 处的切线倾斜角为_
处的切线倾斜角为_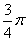
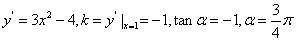
3.函数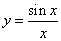 的导数为__
的导数为__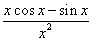 _______________;
_______________;
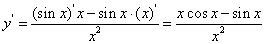
4.曲线 在点
在点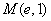 处的切线的斜率是_________,切线的方程为_______________;
处的切线的斜率是_________,切线的方程为_______________;
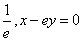
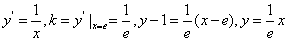
5.函数 的单调递增区间是_____________________
的单调递增区间是_____________________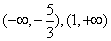
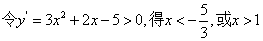
三、解答题
1.求垂直于直线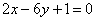 并且与曲线
并且与曲线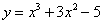 相切的直线方程。
相切的直线方程。
解:设切点为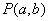 ,函数
,函数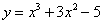 的导数为
的导数为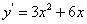
切线的斜率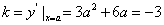 ,得
,得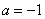 ,代入到
,代入到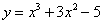
得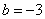 ,即
,即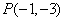 ,
,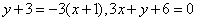 。
。
2.求函数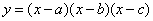 的导数。
的导数。
解: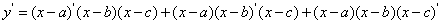
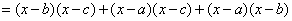
3.求函数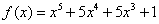 在区间
在区间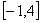 上的最大值与最小值。
上的最大值与最小值。
解: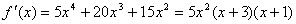 ,
,
当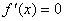 得
得 ,或
,或 ,或
,或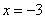 ,
,
∵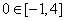 ,
,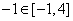 ,
,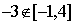
列表:

又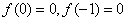 ;右端点处
;右端点处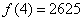 ;
;
∴函数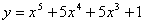 在区间
在区间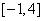 上的最大值为
上的最大值为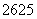 ,最小值为
,最小值为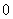 。
。
4.已知函数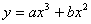 ,当
,当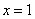 时,有极大值
时,有极大值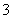 ;
;
(1)求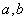 的值;(2)求函数
的值;(2)求函数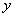 的极小值。
的极小值。
解:(1) 当
当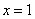 时,
时,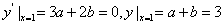 ,
,
即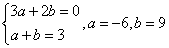
(2)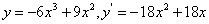 ,令
,令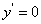 ,得
,得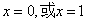
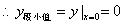
-
高中数学选修2-2知识点总结(精华版)
数学选修22知识点总结一导数1函数的平均变化率为fx2fx1fx1xfx1yfxxx2x1x注1其中x是自变量的改变量可正可负可零…
-
高中数学人教版选修2-2导数及其应用知识点总结
数学选修2-2导数及其应用知识点必记1.函数的平均变化率是什么?答:平均变化率为f(x2)?f(x1)f(x1??x)?f(x1)…
-
高中数学选修2-1、2-2知识点小结
选修2122知识点选修21第一章常用逻辑用语1命题及其关系四种命题相互间关系逆否命题同真同假2充分条件与必要条件p是q的充要条件p…
-
高中数学选修2-2知识点总结
导数及其应用一.导数概念的引入数学选修2-2知识点总结1.导数的物理意义:瞬时速率。一般的,函数y?f(x)在x?x0处的瞬时变化…
-
高中数学选修1-2知识点总结
知识点总结选修12知识点总结第一章统计案例1线性回归方程变量之间的两类关系函数关系与相关关系制作散点图判断线性相关关系线性回归方程…
-
高二数学选修2-1知识点总结
高二数学上期末复习部分知识点概要20xx15高二数学选修21知识点1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的…
-
高中数学选修2-1知识点总结
高二数学选修21知识点1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句2若p则q形式的命题…
-
人教版高中数学选修2-1知识点小结
选修21知识点选修21第一章常用逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句2…
-
高中数学文科选修1-2知识点总结
高中数学选修12知识点总结第一章统计案例1线性回归方程变量之间的两类关系函数关系与相关关系制作散点图判断线性相关关系线性回归方程y…
-
高中数学选修2-1知识点总结
高二数学选修21知识点第一章常用逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句2…
-
高中数学人教版选修2-2导数及其应用知识点总结
数学选修2-2导数及其应用知识点必记1.函数的平均变化率是什么?答:平均变化率为f(x2)?f(x1)f(x1??x)?f(x1)…