复习二   整式的乘除与因式分解

一、整式的有关概念

1、代数式：用运算符号把数或表示数的字母连接而成的式子叫做代数式。单独的一个数或一个字母也是代数式。

2、单项式：只含有数字与字母的积的代数式叫做单项式。

注意：单项式是由系数、字母、字母的指数构成的，其中系数不能用带分数表示，如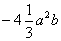，这种表示就是错误的，应写成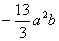。一个单项式中，所有字母的指数的和叫做这个单项式的次数。如是6次单项式。

多项式

1、多项式：几个单项式的和叫做多项式。其中每个单项式叫做这个多项式的项多项式中不含字母的项叫做常数项。多项式中次数最高的项的次数，叫做这个多项式的次数。

①单项式和多项式统称整式。

②用数值代替代数式中的字母，按照代数式指明的运算，计算出结果，叫做代数式的值。

③注意：

（1）求代数式的值，一般是先将代数式化简，然后再将字母的取值代入。

（2）求代数式的值，有时求不出其字母的值，需要利用技巧，“整体”代入。

2、同类项：所有字母相同，并且相同字母的指数也分别相同的项叫做同类项。几个常数项也是同类项。

3、去括号法则

①括号前是“+”，把括号和它前面的“+”号一起去掉，括号里各项都不变号。

②括号前是“﹣”，把括号和它前面的“﹣”号一起去掉，括号里各项都变号。

二、整式的运算法则

1、整式的加减法：（1）去括号；（2）合并同类项。

2、整式的乘法：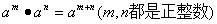

           

           

           

           

           

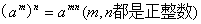
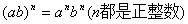
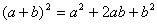
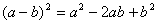
（1）、合并同类项：把多项式中的同类项合并成一项，叫做合并同类项.

例如：；；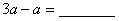

     

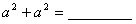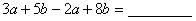
（2）、同底数幂的乘法法则：a^m·aⁿ=a^m+n(m，n是正整数).

同底数幂相乘，底数不变，指数相加.

例如：；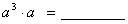

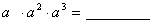
（3）、幂的乘方法则：(a^m)ⁿ=a^mn(m，n是正整数).

幂的乘方，底数不变，指数相乘.

例如：；；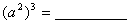

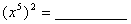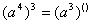
（4）、积的乘方的法则：(ab)^m=a^mb^m(m是正整数).

积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘.

例如：；；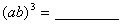

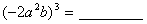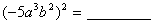
（5）、同底数幂的除法法则：a^m÷aⁿ=a^m-n(a≠0，m，n都是正整数，并且m＞n).

   同底数幂相除，底数不变，指数相减. 规定：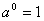

例如：；；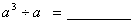

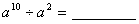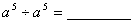
3、整式的除法：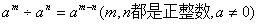

注意：

（1）单项式乘单项式的结果仍然是单项式。

（2）单项式与多项式相乘，结果是一个多项式，其项数与因式中多项式的项数相同。

（3）计算时要注意符号问题，多项式的每一项都包括它前面的符号， 同时还要注意单项式的符号。

（4）多项式与多项式相乘的展开式中，有同类项的要先合并同类项。

（5）公式中的字母可以表示数，也可以表示单项式或多项式。

（6）

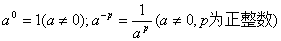
（7）多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加，单项式除以多项式是不能这么计算的。

三、因式分解（整式乘法的逆运算）

1、因式分解：把一个多项式化成几个整式的积的形式，叫做把这个多项式因式分解，也叫做把这个多项式分解因式。

2、因式分解的常用方法

（1）提公因式法：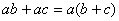

（2）运用公式法：平方差

                 完全平方和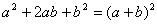

                 完全平方差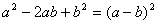

（3）分组分解法：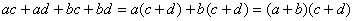

（4）十字相乘法：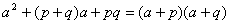

3、因式分解的一般步骤：

（1）如果多项式的各项有公因式，那么先提取公因式。

（2）在各项提出公因式以后或各项没有公因式的情况下，观察多项式的项数：二项式可以尝试运用公式法分解因式；3项式可以尝试运用公式法、十字相乘法分解因式；4项式及4项式以上的可以尝试分组分解法分解因式

（3）分解因式必须分解到每一个因式都不能再分解为止。

◆  例题讲解

1、提公因式法

                       

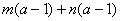
2、公式法

（1）、平方差公式：

            

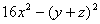
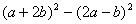
（2）、完全平方公式：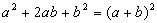   

              

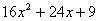
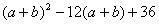
3、分组分解法：

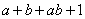       ab－c＋b－ac            a²－2ab＋b²－c²  

4、“十字相乘法”：即式子x²+(p+q)x+pq的因式分解. x²+(p+q)x+pq=(x+p)(x+q).

（1）x²＋7x＋6             （2）、x²－5x－6         （3）、x²－5x＋6

 

第二篇：因式分解经典例题分析

一、                 例题分析

例1  下列从左到右的变形，属于因式分解的有（    ）

A、（x+3）(x－2)=x²+x－6                 B、ax－ay－1=a（x－y）－1

C、8a²b³=2a²·4b³                              D、x²－4=（x+2）（x－2）

分析：本题考查因式分解的意义，考查学生对概念的辨析能力。要将各个选择项对照因式分解的定义进行审查。A是整式乘法，显然不是因式分解；B的右端不是积的形式，也不是因式分解；C的左端是一个单项式，显然不是因式分解；D是将一个多项式化成两个整式的积，符合因式分解的定义。所以选D。

例2          把3ay－3by+3y分解因式

解：原式=3y（a－b+1）

例3          把－4a³b²+6a²b－2ab分解因式

解：原式= －（4a³b²－6a²b+2ab）

        = －（2ab·2a²b－2ab·3a+2ab·1）        这一步要记得变号

        = －2ab（2a²b－3a+1）                这一步不要漏提最后的1

 

例4          把－2p²（p²+q²）+6pq（p²+q²）分解因式

解：原式=－2p（p²+q²）（p－3q）               这里很容易漏掉p

例5          把5（x－y）²－10（y－x）³分解因式

解：原式=5（x－y）²+10（x－y）³    公式（x－y）ⁿ= －（y－x）ⁿ（n为奇数）
                                      （x－y）ⁿ=   （y－x）ⁿ（n为偶数）

        =5（x－y）²[1+2（x－y）]    因式分解要彻底，最后的答案要化简

        =5（x－y）²（1+2x－2y）

例6          把下列各式分解因式：

（1）4x²－9；      （2）x－xy²          （3）x⁴－1           （4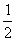）－n²+2m²

解：（1）原式=（2x）²－3²=（2x+3）（2x－3）

   （2）原式=x（1－y²）                      要先提公因式

            =x（1+y）（1－y）                 然后再用公式

   （3）原式=（x²+1）（x²－1）                 分解一定要彻底

            =（x²+1）（x+1）（x－1）            所以……

   （4）原式= 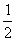－（n²－4m²）       提出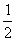－后出现符合平方差公式的式子

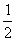            = －（n+2m）（n－2m）

例7          把下列各式因式分解：

（1）－x²+4x－4   （2）（a+b）²+2（a+b）+1 （3）（x²+y²）²－4x²y²

解：（1）原式= －（x²－4x+4）=－（x－2）²

   （2）原式= （a+b+1）²

   （3）原式= （x²+y²+2xy）（x²+y²－2xy）            先用平方差公式

            =  （x+y）²（x－y）²                   再用完全平方公式

例8          分解因式：7x²－3y+xy－21x

解法1：7x²－3y+xy－21x                      解法2：7x²－3y+xy－21x

           =（7x²+xy）+（－3y－21x）                    =（7x²－21x）+（xy－3y）

           = x（7x+y）－3（7x+y）                          =7x（x－3）+y（x－3）

           = （7x+y）（x－3）                                  =（x－3）（7x+y）

总结：分组的方法不是唯一的，但也并不是任意的，分组时要目标明确，首先应当使分组后每组都可以分解因式，其次每组分解因式后各组合在一起又可以分解因式。

例9          把下列各式分解因式：

（1）1－x²+4xy－4y²           （2）x²－4xy+4y²－3x+6y

解：（1）原式=1－（x²+4xy－4y²）

            =1－（x－2y）²

            =（1+x－2y）（1－x+2y）

   （2）原式=（x²－4xy+4y²）+（－3x+6y）  分成两组后一组用完全平方公式

            =（x－2y）²－3（x－2y）        另一组可提公因式

            =（x－2y）（x－2y－3）

例10      （思维训练）分解因式：x²－2xy+y²－2x+2y+1

解：原式=（x²－2xy+y²）+（－2x+2y）+1          分成三组

        =（x－y）²－2（x－y）+1                形成完全平方式的形式

        =（x－y－1）²