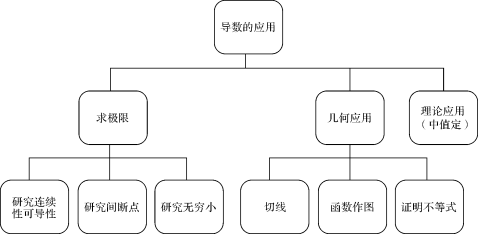
考研数学:微积分考点总结
考研数学:微积分考点总结
一、历年微积分考试命题特点
微积分复习的重点根据考试的趋势来看,难度特别是怪题不多,就是综合性串题。以往考试选择填空题比较少,而今年变大了。微积分一共74分,填空、选择占32分。第一是要把基本概念、基本内容有一个系统的复习,选择填空题很重要。几大运算,一个是求极限运算,还有就是求导数,导数运算占了很大的比重,这是一个很重要的内容。当然,还有积分,基础还是要把基本积分类型基础搞清楚,定积分就是对称性应用。二重积分就是要分成两个累次积分。三大运算这是我们的基础,应该会算,算的概念比如说极限概念、导数概念、积分概念。
二、微积分中三大主要函数
微积分处理的对象有三大主要函数,第一是初等函数,这是最基础的东西。在初等函数的基础上对分段函数,在微积分的概念里都有分段函数,处理的一般方法应该掌握。还有就是研究生考试最常见的是变限积分函数。这是我们经常遇到的三大基本函数。
三、微积分复习方法
微积分复习内容很多,题型也多,灵活度也大。怎么办呢?这其中有一个调理办法,首先要看看辅导书、听辅导课,老师给你提供帮助,会给你一个比较系统的总结。老师总结的东西,比如说我在辅导课程中总结了很多的点,每一个点要掌握重点,要举一反三搞清楚。从具体大的题目来讲,基本运算是考试的重要内容。应用方面,无非是在工科强调物理应用,比如说旋转体的面积、体积等等。在经济里面的经济运用,弹性概念、边际是经济学的重要概念,包括经济的函数。还有一个更应该掌握的,比如集合、旋转体积应用面等等,大的题目都是在经济基础上延伸出的问题,只有数学化了之后,才能处理数学模型。
还有中值定理,还有微分学的应用,比如说单调性、凹凸性的讨论、不等式证明等等。应用部分包括证明推断的内容。
总的来说,学好微积分,就是要掌握三个基本函数、三大运算,所以广大研友们要在这些方面多下功夫!
小提示:目前本科生就业市场竞争激烈,就业主体是研究生,在如今考研竞争日渐激烈的情况下,我们想要不在考研大军中变成分母,我们需要:早开始+好计划+正确的复习思路+好的辅导班(如果经济条件允许的情况下)。2017考研开始准备复习啦,早起的鸟儿有虫吃,一分耕耘一分收获。加油!
第二篇:考试点 白云霄、桑园20xx考研数学《微积分》考点精讲与过关习题(数三)

考点精讲
目 录
第一章 函数???????????????????????????????????(1)
第二章 一元微分学????????????????????????????????(3)
第三章 一元函数积分学?????????????????????????????(28)
第四章 多元函数微分学?????????????????????????????(45)
第五章 二重积分????????????????????????????????(53)
第六章 微分方程????????????????????????????????(58)
第七章 无穷级数????????????????????????????????(66)
《微积分》考点精讲
第一章 函 数
一、函数的定义:
1.函数的两大属性:定义域,对应法则
【例1】 下列函数是否相同
(1)f(x)=ln(1-x2),g(x)=ln(1+x)+ln(1-x)
(2)f(x)=ln(x2-1),g(x)=ln(x+1)+ln(x-1)
解 (1)定义域均为-1<x<1,对应法则相同,f(x)=g(x);
(2)f(x)的定义域为|x|>1,g(x)的定义域为x>1,f(x)与g(x)不同.2.函数的解析式
【例2】 (已知解析式)
(1)设f(x)x
1+x,求f(1),1
x),f(f(x))
解 f(1)11
1+12
1
1
x)x1
111+x
x
x
f(f(x))f(x)1+xx
1+f(x)1x1+2x
1+x
(2) 设f(x)x求f(f(x)),f[f…f(x)+x]
{n
x
解 f(f(x))f(x)+xx
+f(x)1x+21+x2x归纳得:f[f…f(x)]x
+nx【例3】 (未知解析式)
(1)f(ex)=x+1,求f(x).
解 令ex=t x=lnt f(t)=lnt+1
即f(x)=lnx+1 x>0
(2)f(x1
x)=x21
x2,f(x)=
解 f(x1
x)=(x1
x)2-2
—1—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
2∴f(x)=x-2 |x|≥2
二、函数的性质
1.奇偶性
x-x),e-e,f(x)+f(-x)(偶),几种常见的奇、偶函数:sinx,cosx,ln(x++x,y:f(x+y)=f(x)+f(y)(奇)x
【例4】 研究f(x)=ln(x++x)的奇偶性
1解 f(-x)=ln(x++x)=l=-f(x)x++x
∴f(x)为奇函数.
2.有界性
22xx2,闭区间上的连续函数,有极限与有界几种常见的有界函数:sinx,arcsinx,x-[x]221+xx+y
的关系等
【例】 设f(x)∈C(-∞,+∞),且limf(x)=A,证明:f(x)有界x→∞
证明 ∵limf(x)=A ∴M X>0当|x|>X1>0x→∞
|f(x)|≤M1
当|x|(x)在[-X,X]连续,使≤X时fM2>0
|f(x)|≤M2
以M=max{M,M} x-∞,∈(∞)12
|f(x)|≤M
三、几种特殊函数
(1)f(x)=[x]
(2)f(x)=sgnx:xsgnx与的关系
(3)分段函数
(4)复合函数
x2e,xx+1,x>0≥0【例5】 设f(x)=,g(x)=2xx,x<0e,x≤0{{
求f(g(x))
解 f(g(x)={x+1 x>0e
eex2x≤0
xx+2,x<0e,x<1例6 设f(x)=,g(x)=求f(g(x))2x,xx-1,x≥1≥0{{
x+2 x<-1?e,
?,-1≤x<0?x+2解 f(g(x))=?2x-1e,0≤x<??
2?x-1,x≥—2—
《微积分》考点精讲
第二章
一元微分学
一、求导数
1.导数公式
2.求导类型
(1)利用运算法则求导
【例1】 求下列函数的导数(f(x)可导)
f(x)x22x2+x+2;xe;xf(x)x
x22x2解 (2+x+2)′=2ln+2x
xx(xe)′=(x+1)e
(xf(x))′=f(x)+xf′(x)
f(x)xf′(x)-f(x))′=2xx
已知f(x)=x(x+1)(x+2)…(x+2013),f′(0)=2013!(3)复合函数的导数
2fx(e)·ex的导数【例2】 求复合函数y=[arctan],y=f()
2arctaarcta2,y′解 y=(arcta1+x)1+x)xf(x)xxf(x)xf(x)y=f(e)·e,y′=f′(e)ee+f(e)·ef′(x)
11)=sinx,求fx),f′(f(x)),[f(f(x))]′【例3】 22
—3—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
解 由1
2x)=2sinx得f(x)=sin2x,f′(x)=2cos2x
f1
2x)=2cosx,f′(f(x))=2cos(2sin2x)
[f(f(x))]′=f′(f(x)),f′(x)=2cos(2sin2x)·2cos2x
=4cos(2sin2x)·cos2x
同学们要大量练习,做到熟能生巧
(4)参数方程所确定的函数的导数
2
例4 设{x=ln1(+t2)
y=t-arctant,求dydy
dxdx2.
dy11
解 dydt1+2t
dxt
dx2t2
dt1+t2
dy′1
d2ydt21+t2dx2dx2t4t
dt1+t2
【例5】 设在极坐标下ρ=2θ,求dy
dx
解 {x=ρcosθ=2θcosθ
y=ρsinθ=2θsinθ
dydydθsin+cos
dxθθθ
dxcosθ-θsinθ
dθ
(5)隐函数求导
【例6】 设ey-xy=1,求y′(0)
解 两边对x求导
eyy′-y-xy′=0
y′y
ey-x y′(0)=0
【例7】 设y=tan(x+y),求y″
解 两边对x求导
y′=sce2(x+y)(1+y′),y′=-csc2(x+y)
y″=2csc2(x+y)cot(x+y)·(1+y′)
=2csc2(x+y)cot(x+y)·(1-csc2x+y)
【例8】 设y=sinx·x3·-x,求y′
解 两边取对数 lny1
2(lnsinx+3lnx1
2ln1-x2)
—4—
y′
y1
2cosx3x
sinxx1-x2)
y′=sinx·x3·-x·1cosx3x
2sinxx1-x2)
(6)幂指函数的导数
【例9】 y=xx,求dy
dx
解 y=exlnx y′=xx(lnx+1)
【例10】 设y=x2
1+xx,求y′
解 y=exx2
=ex(2lnx-ln1+x)
y′=x2x21
1+x)x[l2
1+x2+xx1+x)]
(7)高阶导数
常用公式:
1.(xn)(n)=n!,(xn)(m)=0(m>n).(m,n均为自然数)2.(ex)(n)=ex,(ax)(n)=?,(eax)(n)=?解 (ax)(n)=axlnna (eax)(n)=eaxa3.(sinx)(n)=sin(xnπ)(n)
2,(cosx)=cos(xnπ)(n)
2,(sin(ax+b))=?
解 [(sin(ax+b))](n)=ansin(ax+bnπ
2)
4.(1(n)(-1)nn!
a+x)(a+x)n+1
n
5.(ln(1+x))(n)=(1(-1)(-1)n-1(n-1)!
1+x)(1+x)n
【例11】 (sin(2x+3))(10),(cos2x)(20)(1(5)1(4)
2x+1)(x2-2x-3)
解 [sin(2x+3)](10)=210sin(2x+3+5π)=-210sin(2x+3)
(20)(2
(cos2x)=1+cos2x(0)
2)1
220cos(2x+10π)=219cos2x
(1
+1)(5)5-1)55!
2x=2(
(2x+1)6
(1(4)
x2-2x-3)=1
(x-3)(x+1)](4)=1(14x-31)()
x+1]4
1(4!4!
4(x-3)5(x+1)5)
=3!(1
(x-3)51(x+1)5)
—5—《微积分》考点精讲
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
(n)k()(k)6.(u·v)=∑cun-kvnk=0
2-(n)【例12】 y=xex,求y
(n)k-x()2()解 y=∑C(e)n-k(x)k
nk=0
0-x()21-x()2-x()=C(e)nx+C(e)n-1·2x+C(e)n-2·2nnn
0(n)-21(n)-n-22-=C(-1)exx+C(-1)ex·(2x)+2(-1)Cex
nnnnn
(8)积分上限函数的导数
dx1.(f(t)dt)′=f(x),或f(t)dt=f(x);adxa∫x∫
【例13】 设φ(x)=
2′(x)=sinx解 φsintdt,求导数φ′(x).∫21x
设φ(x)=intdt,求导数φ′(x),.φ(π
2)1x
ππ解 φ′(x)=-inx φ=-si24()2.如果F(x)=∫0(x)f(t)dt,则F′(x)=
2x(t)dt=f((x))′(x).φφ(∫f)′0(x)【例14】求函数(x)=
解 φ′(x)=2xsinx
3.如果F(x)=sit的导数.∫0(t)dt,则F′(x)=f((x))′(x)-f((x))′(x).φφψψ∫f(x)ψ(x)φ
d2costdt.【例15】 求2dxxd
解 2costdt2cosxx4-2xcosxdx24.F(x)=(x-t)f(t)dt,F′(x)∫0
x
0x.(x-t)g(t)dt,求f′(x),f″(x).∫【例16】 设g(x)处处连续,f(x)=
(t)dt-解 f(x)=xg0∫xtg(t)dt∫0
x
0xf′(x)=g(t)dt+xg(x)-xg(x)=∫g(t)dt∫0
xxf″(x)=g(x)5.F(x)=sin(x-t)dt,F′(x)∫2
0.
解 令x-t=u F(x)=sinudu∫2
0x
2F′(x)=sinx
—6—
《微积分》考点精讲
【例17】 设f(x)连续,求函数F(x)=
f(u)du∫解 令xt=u F(x)0xf(xt)dt(x>0)的导数.∫01
x
xf(x)-f(u)du0F′(x)2x
6.设f(x)连续,F(x)=(t)dt,F′(x)x-f0
11
0001∫x.1(x)=解 当x≥1时 F(x-t)f(t)dt=xf(t)dt-∫tf(t)dt∫∫
f(t)dt∫01F′(x)=
当x(x)=≤0时 F∫0
x1(t-x)f(t)dt=f(t)dt∫01∫011tf(t)dt-xf(t)dt0∫1F′(x)=-当0<x<1 F(x)=∫0
x
0
x(x-t)f(t)dt+x(t-x)f(t)dt∫x11xx=xf(t)dt-F′(x)=
=∫0xtf(t)dt+∫tf(t)dt-xf(t)dt∫∫01xf(t)dt+xf(x)-xf(x)-xf(x)-∫f(t)dt+xf(x)∫f(t)dt-∫f(t)dt∫0x1
(9)函数在一点的导数
12xxsi≠0x【例18】 已知f(x)=,试讨论在x=0的可导性.0x=0
12xsi-0f(x)-f(0)x=lim=0解 limxxxx-0-0→0→0
∴f′(0)=0,f(x)在x=0处可导
x xe≥0在x=0连续,试讨论在x=0的可导性.【例19】 已知f(x)=cosxx<0
xf(x)-f(0)e-1解 f′(0)=lim=lim=1+x-0xxx→0+→0+{{
f′0)=lim-(f(x)-f(0)cosx-1=lim=0x-0-0xx→0-→0-x
∴f′0)′0)≠f+(-(
f(x)在x=0处不可导
,y,f(x)f(y)=f(x+y),f′(0)=2,求f(x)【例20】 已知x
—7—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
解 f′(x)=limf(x+x)-f(x)f(x)·f(x)-f(x)x)-f(0)f(=lim=limf(x)·xxxΔΔΔxxx→0→0→0ΔΔΔ
=f′(0)f(x)=2f(x)
2∵f(0)可以求出为1(f(0)=f(0) f(0)=0或1 如果f(0)=0 f(x)=f(x)·f(0)=0
f′(x)=0与f′(0)=2不符)
由f′(x)=2f(x)可知f(x)=e2x
(10)分段函数的导数
【例21】 已知f(x)={x2arcta1
x x≠0, 求f′(x)
0 x=0
解 x≠0,f′(x)=2xarcta1
xx2
1+x2
x2arcta10x=0,f′(0)=lx-
xi→m0x-0=lxi→m0xarcta1x=0
(11)反函数的导数
【例22】 用y′,y″,y来表示dxd2xd3x
dydy2dy3,
并化简微分方程d2xdx3
dy2+(y+sinx)dy)=0
解 dx1
dyy′
11
d2xy′yxy″1y″
dy2dy′
dx·ddyy′2·y′y′3
d2xd(y″)(y″
y′3dy′3)dxyy′3-3y′2y″21yy′-3y″2
dy3dydxdy(y′)6·y′
y′5
d2x
dy2+(y+sinx)(dx)3dy=0可化简为
y″
y′3+(y+sinx)·1y′3=0
即y″-y=sinx
第一节 求极限
1.求极限的方法归类:
1)洛必达法则;
2)等价无穷小因子代换;
3)无穷小与有界量之积为无穷小
—8—
4)重要极限
5)导数的定义
6)夹逼准则
7)定积分的定义
8)单调有界原理
9)泰勒公式
2.多项式的极限
【例1】 求极限lxi→x+3x-3-13x2+9;xl→i3x2-9;xl→i1-1解 lxi→mx+33x2+91
3
limx-3
x→3x2-9=lxi→m13x+316
11
l-12xxi→m1-1=lxi→m113
22
3x?0 n<m
ann-1?0x+a1x+…+an-1x+an?a0xln=→i∞b0xm+b1xm-1+…+b=?m-1x+bm?bm
?0
?∞n>m
【例3】 求极限(3x4+2x2+x+6)3(2x2-3)9
xl→i∞(5x6-4x3+7)4(x3-1)23
解 原式3·29
54
【例4】 lx→ix3+2x2-12∞x+2+ax+bx=1,a=?,b=?323解 lx→imx+2x-1∞x+2+ax2+bx=xl→imx+2x2-1+(ax2+bx)(x+2)∞x+2=1{1+a=0
2+2a+b=0 ∴a=-1 b=03.重要极限1x1∞xl→im∞(1x)=e或lxi→m0(1+x=e(1型)
【例5】 求极限()(x2+x+11
nl→im∞11nn;xl→im12+2)2x∞x2;lxi→m0(cosx解 l(1
n→im∞1n)-n·n=e-1
2+12x1-(x+2)·2x2+1lim=-(x+2)x→∞(xx2+2)2+xl→im11∞(x2+2)2=e-2lim(cosx1lim(cosx1lim(1-s1-sin2x
xx→0=22xx→0=in2x-sinx·=e12xx→0
—9—《微积分》考点精讲
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
4.无穷小与有界量之积为无穷小
12xsi+sinxxnsinn1,li2,lim(【例6】 lix-[x])sixnxx→0→∞n+→∞2n-1x
12sinxxsi+xsinx1=limlim=0+1=1解 lixsi+xxxxx→0→0→0x
nsinnn=lim2·sinn=0li2n→∞n+→∞n+2n-1n2n-1
11im(0lim(x-[x])si=lx-[x])·=xxxx→∞→∞
5.等价无穷小因子代换
常用的几个等价代换公式:当x→0时,
xsinx~x,tanx~x,arcsinx~x,arctanx~x,e-1~x,ln(1+x)~x
2xx(1+x)-a1~x,1-cosx,-1~xlnaα2α
+sinx-1tanx-sinxe-e111n,【例7】 (1)li,(2)li,(3)limxcsl(4)li2,x→02xx→03sinxx→∞x(x)3xxx→0x
1-(5)lix→0+(1-cox12inx+sinx-121解 (1)li=lim22xx2→0→0xxtanx-sinxtanx(1-cosx)=lim(2)li=lim33xxx→0→0→0sinxxx·122132x
11111csllim·2=1(3)limxn2=x1xx→∞→∞xx
x
3xx2xe-e12xxe-=lim=lim=2(4)lie·xxxxx→0→0→0x()
12x21-1-1-cosx111(5)li=lim··=lim=lim121222xx→0+(→0+→0+→0+121-coxxx1+xxx222
6.导数的定义
【例8】 已知函数f(x)在x试问A与f′(x)的关系?0点可导,0
f(x2x)-f(x)Δ0+0(1)A=li=xΔx→0Δ
f(x2x)-f(x)f(x2x)-f(x)ΔΔ0+00+0=lim·2=2f′(x解 A=li)0xxΔx2x→0→0ΔΔ
f(xh)-f(xh)0+0-=(2)A=lihh→0
—10—
《微积分》考点精讲
f(xh)-f(xh)f(xh)-f(x)+f(x)-f(xh)0+0-0+000-解 A=li=lim=2f′(x)0hhhh→0→0
7.数列的极限
【例9】 求数列和的极限
(1)limn→∞(111+…·3n·(n+11·22))
)()111111…解 原式=lim1+=lim1=1n223nn+1n+1n→∞→∞
(2)limn→∞(11+…1+2n+n+1
1解 ∵≤11111+…+…+n+n+n+1+2n+n11+…+1n+1+11
n→∞而lim(1n+…=lim=1n→∞+n+n+n11n→∞lim(1+…=1n+1+11
∴原式=1(3)limn→∞n+11
n+21+…2n+n1?1?解 原式=lim?n→∞n?
=(4)limn→∞1??+???1+?n?10??+…+???1+?n?(1=ln12???1+n?12x=ln+x01x++x11+…(n1)+1n+2n+n
111?+…1?解 原式=lim?n??11121?n→∞nnnn??
1(1+x)dx-ln=01+x11
02=ln
2nπππsisisinnn(5)lim+…)n12n→∞nnnnnn
2nπππsisisi2nnnn1πππsi+si+…+si解 ∵+…≤nnn12nnnnnnnn()—11—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
2nnsisisisisinnnnn+…+…≤n+1n+1n+11nnnn
n1ππ…+sisi+=而limnnn→∞n
n→∞2sinxdxπ()∫πnn1n12si+…+sisi+…+si·lim=lim=∫sinxdxπ()()nnnnn+1n+1nπ101n→∞0
2∴原式π
?2?(6)limsinn?→∞?11n11n
+…1??1n?111???11?nn?2?解 原式=li?n→∞n?11n11n+…1=2x-limn10n→∞=4-1)【例11】 其它数列的极限
n→∞+3lim解 ∵+3+3=3≤≤又∵lim=3 lim3·=3n→∞
n→∞∴lim+3=3n→∞8.单调有界原理
xn=2,3,…;试证明limx并求出极限值【例12】 (1)设x1n=n-1n存在,n→∞
解 单调性:xx>x 不妨设xx2=1=11>k-1xxk-1=k>k-1=k
∴xn单调增加
<2,不妨设x2 x=2有界性:x1k<k+1=k<∴x2n<
于是用单调有界原理 limxn存在设为An→∞
对x A=则A=2n=n-11,xn=2,3,…;试证明limx并求出极限(2)设0<x1<n+1=nnn存在,n→∞
证明 xn+1=nn
∴xn有上界3322
—12—
《微积分》考点精讲
xn+1nn=-1≥1xxxnnnxn单调增加
∴limx 两边求极限n存在设为An→∞
3A=A2
9.洛必达法则
0【例13】 型)0
x-sinxx-arcsinxx-ln(1+x)e-(1+x(1)li3 ((4)li2)li (3)li3xxxxxx(1+cosx)xsin→0→0→0→0xsinx1
sintdt∫(5)li20
x→02(x-sinx)2x
12xx-sinx1-cosx12解 (1)li3=li=li32xxx→0→03→03xxx6
x-arcsinxx-arcsinx(2)li=li=li33xxx→0→0→0sinxx112x21-x=li22x6→033xx1
1x11+x-ln(1+x)x-ln(1+x)x1+x1=li=li=li(3)li2xxx(1+cosx)xsinxx4xx4→0→0→0→042x
x-ln(1+x)1e-(1+x-[(1+x]′x1+·=li=-lim(4)li(1+x2x0x0x0x1→→→x1111
2x(1+x)1+=-lime·x2x→0
-x
21+x)ee(i2xx2→0
sintdt∫(5)li=li20
x→02(x-sinx)2x4532xsinx2x2x=lili2=xx2(x-sinx)(1-cosx)xx-sinx→0→0→0(x-sin)x
26x=12=lix1-cosx→0
∞【例14】 型) ∞2lnx(1)lim2x∞x+→+1
解 原式=lim2lnx2=lim022=xx∞2∞4→+→+xx
—13—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
xln(1+e)(2)limx∞→++xxe
x1+e解 原式=lim=1x∞x→+
+x【例15】 (0·∞型)
(1)limxlnxx→0+-1lnxxlnx=li-1=li0解 limx-2=xxx→0+→0+x→0+-x
πarctanx)(2)limx-x∞2→+
1-arctanx21+x2解 原式=lim=lim=1-1xx∞∞1→+→+x2x
2)(3)lim(1-x)tanxx2→1
21-x-2x4解 原式=li=lix→1→1πxπ2ππccoxscx222
【例16】 (∞-∞型)
(1)limx→0(
(11xxe-1)xxxe-1-xe-1-xe-11解 原式=lix=li=li2xxx2→0→0→02x(e-x1)x
(2)limx→01122xsinx
2222)122x)(sinx-xsinx-xsin2x-2x2cos2x-221解 原式=li22=li=li=li=li4322xxxx3→0x→0→0→0→04x12xsinxxx6x
本例小结
00∞【例17】 (1,0,∞)
x(1)limxx→0+
-1lnxx解 原式=lime=eli-1=eli1-2=xxx→0+→0+x→0+-xxlnx
sinxx(2)limxx→0+()1
cosx1lnsinx-lnxsinxxxcosx-sinxcosx-xsinx-cosx1解 原式=lim=elim=elim=elim=e2322xxxxx→0+→0+→0+→0+x2x6x
—14—
《微积分》考点精讲
f(x),x≠0x【例17】 设f(x)在(-,+)二阶可导,f(0)=0,g(x)=求g′(x)∞∞
f′(0),x=0
f′(x)x-f(x)解 x,g′(x)≠02x
f(x)-f′(0)g(x)-g(0)xf(x)-f′(0)xx=0,g′(0)=lim=lim=lim2xxxxx-0-0→0→0→0x
=lim
=limf′(x)-f′(0)x2x→0f′(x)-f′(0)(导数定义)x2(x-0)→0{
f″(0)2
2-xln(1+x)+e-110.泰勒公式li6x→0x
4646xxxx166266x+x+o(x)+1-x+o(x)-1o(x)232!3!61解 原式=lim=lim66xx6→0→0xx22
第二节 极限的应用
一、研究分段函数的连续性、可导性
1kxsi x≠0x【例1】 已知fx,试讨论k取何值时在x=0处连续、可导、导函数连续?()=
=0 0 x
>01kk解 limxsif(0) ∴k>0时f(x)在x>0处连续0=xx→0{
lim>1f(x)-f(0)1kk-1=limxsif′(0) ∴k>1时f(x)在x=0处可导0=xxx-0x→0→0
1k-21k-1当xf′(x)=kxsi-xco≠0时,xx
>21k-21kk-1xclimf′(x)=lim(kxsi-of′(0)0=xxxx→0→0
∴当k>2时f′(x)在x=0处连续
(1-cosx)?2,x<02x??=0处连续性【例2】 讨论f(x)=?1,x=0在x
?x2?1costdt,x>0?x0∫
—15—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
costdt∫cosx=lim=1解 f(0+0)=lim202
x→0+xxx→0+1
12x22(1-cosx)f(0-0)=lim=lim=122xx→0-→0-xx
∴f(0+0)=f(0-0)=f(0)=1
于是f(x)在x=0处连续.
【例3】 设f(x)在(-+有二阶连续导数,∞,∞)
-xf(x)-e,x≠0xf(0)=1,f′(0)=-1,g(x)=求g′(x)并讨论g′(x)的连续性.(){
0,x=0
-x-x)x-(f(x)-e)(f′(x)+e解 x′(x)≠0时 g2x
-xf(x)-e-0-xg(x)-g(0)xf(x)-e=lim=limx=0时 g′(0)=lim2xxxxx-0-0→0→0→0x
-x-xf″(0)-1f′(x)+ef″(x)-e=lim=limxx2x22→0→0
-x-xf″(0)-1f″(0)-1(f′(x)+e)x-(f(x)-e)limg′(x)=lim=f″(0)-1=g′(0)2xx22→0→0x
∴g′(x)在x=0处连续
x′(x)显然连续≠0时g
∴g′(x)在(-+连续.∞,∞)
111π1π=+=注意:lim,lim0,limarcta,rctalima∞x2xx2xxx→0+→0-→0+→0-
x→0+x]=0,lim[x]=-1lim[x→0-
【例4】 指出下列函数的所有间断点,并进行分类.
1(1)f(x)=arctax
解 x=0
1πf(0+0)=limarctax2x→0+
1πf(0-0)=limarctax2x→0-
∴x=0为第一类跳跃间断点.
(2)f(x)x(x+2)
2(x-4)
解 间断点有x=0,x=2,x=-2
x=2为无穷间断点
—16—
limx(x+2)x
x→-2|x|(x2-4)=lx→im-2|x|(x-2)1
4
x=-2为第一类可去间断点.
lim)=limx(x+2)
x→0+f(xx→0+x(x2-4)1
2
limf=limx(x+2)1
x→0-(x)x→0--x(x2-4)2
∴x=0为第一类跳跃间断点
(3)f(x)x(x+2)
sinπx
解 间断点x=k k=0±1±2…
x=0为第一类可去间断点 lxi→mx(x+2)x(x0sinπx=lxi→m+2)0πx2
π
x=-2为第一类可去间断点 limx(x+2)
x→-2sinπx=lx→im2x+22-2πcosπxπ
其它的整数点均为无穷间断点
(4)f(x)1
1-x
解 间断点有x=0 x=1
x=0为无穷间断点
f(1+0)=1 f(1-0)=0
x=1为第一类跳跃间断点
(5)f(x)=1-x2n
nl→i∞1+x2nx
x|x|<1
解 f(x)={0|x|=1
-x|x|>1
x=1为第一类跳跃间断点 x=-1为第一类跳跃间断点(6)f(x)=nl→i1-e-nx∞1+e-nx
{1x>1
解 f(x)=0x=0
-1x<1
x=0为第一类跳跃间断点
(7)f(x)=nl→im∞+解 f(x)={|x|3|x|>1
1|x|≤1
f(x)处处连续
—17—《微积分》考点精讲
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
三、研究无穷小
xx【例】 当x2+3-2是x的 1 阶无穷小→0时,
xxx2x32+3-22ln+3ln6解 lim=lim=lnxxx1→0→0
132当x(1+ax-1与cosx-1是等价无穷小a= →0时,2
123解 ∵(1+ax-1∽a212 cosx-1∽x23
3∴a2
把下列无穷小按阶数由高到低排列顺序当x→0时,
costdt,tat,sintdt∫∫23
000x2x解 costdt为1阶无穷小 ∫tat为3阶无穷小 sintdt为2阶无穷小∫23
000x2x第三节 几何应用
一、求曲线的切线
例1 求曲线y4,2)的切线及法线方程.11解 y′k41切线方程为 y-2(x-4)4
法线方程为 y-2=-4(x-4)
x【例2】 求过原点的曲线y=e的切线方程
x0解 设切点为(x,e)0
x0e-0e x=1x00
0-x0
切线为:y=ex
【例3】 求由极坐标表示的曲线ρ=1+cos在θ处的切线方程θ4
解 {x=cos=(1+cos)cosρθθθ+1+1 切点为22y=sin=(1+cos)sinρθθθ()
2ddy-sin+(1+cos)coskθ Rddx-sincos-(1+cos)sinθθθθ2—18—
《微积分》考点精讲
+1+1)x切线方程为:y222+二、曲线的单调性、凹凸性、极值、拐点、渐近线、函数作图.
2x【例4】 求y=1极值、凹凸区间、拐点.2(x-1)
解 略
32【例5】 已知曲线y=x+bx+cx+d上有拐点(1,-1),且在x=0处的切线平行于x轴,求b,c,d
解 1+b+c+d=-1… ①
2y′=3x+2bx+c
c=0…
y″=6x+2b
6+2b=0…
c=0 b=-3 d=1②③
【例6】 设f(x)在闭区间[0,1]上二次可微,且f(0)=0,f″(x)>0,证明函数调增加的.
证明 f(x)在(0,1]上是单x(f(x)f′(x)x-f(x)f′(x)x-(f(x)-f(0))′22xxx
f′(x)x-f′()xξ(0<<x)ξ2x)
∵f″(x)>0f′()<f′(x)ξ
于是(x)f(x)′>0 单调增加(f)xx
【例7】 设y=f(x),y″-2y′-4y=0,f(x)>0,f′(x)=0则f(x)在x=x000处取解 y″=2y′+4y
y″(x)=4y(x)>000
∴x=x0处取极小值
f(x)-f(a)【例8】 若li2则f(x)在x=a处取2=x→a(x-a)
f(x)-f(a)解 li2>02=x→a(x-a)
∴u(a-) δ。f(x)-f(a)0 即f(x)>f(a)2>(x-a)
∴f(a)为极小值
【例9】 设y=f(x)在x=x如果f′(x)=0,f″(x)=0,f(x),≠00的某邻域内具有三阶连续导数.000试问x=xx,f(x))是否为拐点?为什么?0是否为极值点?为什么?又(00
解 不妨设f(x)>00
—19—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
f″(x)-f″(x)f″(x)0f(x)=li=li>00xxxx-xx-x→x→0000
>0 当x(x,) δ∈uδ0。f″(x)>0x-x0
当x<x<x,f″(x)<0 当xx<x f″(x)>0 ∴x=xδδ0-00<0+0为拐点当x<x<x,f″(x)<0 f′(x) f′(x)=0 ∴f′(x)>0δ0-00
当xx<x,f″(x)>0 f′(x) f′(x)=0 ∴f′(x)>0δ0<0+0
得x=x0不是极值点
【例10】 写出下列曲线的渐近线
3xx;(2)y2;(3)y=ln(1+e(1)y2);x+2x-3x+x-2
解 (1)x=-3x=1为垂直线近线
3x32xx+2x-3-x=-=1,b=lim22k=lixxx→0→∞x+2x-3()
y=x-2为斜渐近线
(2)x=-2x=1为垂直渐近线
=1x∞x+→+x-2lim2
=-1x∞x+→-x-2lim2
y=1,y=-1为水平渐近线
x(3)limln(1+e)=0 y=0为水平渐近线x∞→-
xxxxln(1+e)e(1+e)(1+e)x=lim1 b=lim(ln-x)=limln-lne=0k=limx=xxxx∞∞1∞∞x→+→+→+→++e
y=x为斜渐近线
2x+x+1【例11】 y=arcta的渐近线有(x-1)(x+2)1
x解 x=0为水平渐近线ππ(x) y为水平渐近线limfx44→∞三、证明不等式
(1)利用单调性证明
(2)利用极值或最值证明
(3)利用中值定理
(4)利用凹凸性证明
(5)利用泰勒公式证明
—20—
【例1】 证明下列不等式
1)当x>0x
1+x<ln(1+x)<x
证明 令f(x)=x-ln(1+x)f(0)=0 f′(x)=11
1+x>0
∴f(x)>0 即ln(1+x)<x令g(x)=ln(1+x)x
1+x
g(0)=0 g′(x)1
1+x1
(1+x)2>0
∴g(x)>0 即x
1+x<ln2(1+x)
2)当0<x<1时,(1+x)ln2(1+x)<x2证明 令f(x)=x2-(1+x)ln2(1+x)f(0)=0 f′(x)=2x-ln2(1+x)-2ln(1+x)f′(0)=0 f″(x)=2-ln(1+x)
1+x2
1+x=x-ln(1+x)
1+x>0
f′(x)>0近而f(x)>0
即 (1+x)ln2(1+x)<x2
3)设x>0,当a>e时,证明:(a+x)a<aa+x证明 令f(x)=(a+x)lna-aln(a+x)
f(0)=0
f′(x)=lnaa
a+x>0
∴f(x)>0
即(a+x)lna>aln(a+x)
化简可得(a+x)a<aa+x
4)设b>a>0,求证:lb
a2(b-a)
b+a
证明 令f(x)=lnx-lna2(x-a)
x+a
f(a)=0
f′(x)1
x4a(x-a)2
(x+a)2x(x+a)2>0
∴f(x)>0
即 lnx-lna2(x-a)
x+a
取x=b可得
—21—《微积分》考点精讲
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
b
2(b-a)
b+a
5)设e<a<b<e2,证明ln2b-ln2a4e2(b-a)
证明 令F(x)=ln2x-ln2a4e2(x-a)
F(a)=0
x
F′(x)=ln4xe2
xF″(x)=1-ln
x2<0
F′(e2)=0
∴F′(x)>0从而F(x)>0取x=6可得
ln2b-ln2a4e2(b-a)
【例2】 证明下列不等式
1)1+xln(x++x)≥+x证明 令f(x)=1+xln(x++x)-+xf′(x)=ln(x++x) f′(0)=0
f″(x)1x=0为最小值点+xf(x)≥f(0)=0 即1+xln(x++x)≥+x2)设f(x)在(0,+∞)上二次可微,f(0)=0,f″(x)<0,证明:对x1>0,x2>0,f(x1+x2)<f(x1)+f(x2)证明 不妨设x1<x2
f(x1)-f(0)=f′(ξ1)x1 0<ξ1<x1
f(x1+x2)-f(x2)=f′(ξ2)x1 x2<ξ2<x1+x2f″(x)<0 f′(x) f′(ξ2)<f′(ξ1)
f(x1)-f(0)>f(x1+x2)-f(x2)
即f(x1)+f(x2)>f(x1+x2)
3)xlnx+ylny>(x+y)lx+y
2(x>0,y>0,x≠y)
证明 研究f(x)=xlnx的凹凸性
f′(x)=lnx+1 f″(x)1
x>0 f(x)为凹
xyxlnx+ylny+yx+y
2x
2l2
即 xlnx+ylny>(x+y)lx+y
2
—22—
《微积分》考点精讲
2sinxx4)证明:当0<x时,2π
sinx证明 研究f(x)的单调性x
xcosx-sinxxcosx-(sinx-sino)f′(x))<0=(cosx-cosξxx
si22sinxπf(x)> 2xππ
2()
2即 sinxπ
【例3】 设函数f(x)在[a,b]具有二阶连续导数,f′(a)=f′(b)=0,证明:a,b),ξ∈(≥f″(ξ4(b)-f(a2f(b-a)
f″()ξ12(x-a)证明 f(x)=f(a)+f′(a)(x-a)!2
)f″(ξ22f(x)=f(b)+f′(b)(x-b)(x-b)2!
a+b取x2
2)(f″(ξa+bb-a)1…①=f(a)22!4()
f″(ξ)(a+bb-a)=f(b)…②(2)2!422
①-②得
2″(f″()f)ξξ(b-a)12O=f(a)-f(b)422()
f″()-f″(f″()+f″(介值定理fξξξξf(b)-f(a″(ξ1212≤2222(b-a)四、证明等式
11)证明:x>0时arcta+arctanxx2
1πarctanx证明 令f(x)=arcta+x211f′(x)022=1+x1+x
f(x)=C f(1)=0 C=0
1arctanx即 arcta+x2
—23—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
2)设f(x)是l以为周期的连续函数,证明:对任意的常数a,有:
f(x)dx=∫f(x)dx∫a0a+ll
d
证明
∴a+l
af(x)dx∫=f(a+l)-f(a)=0aa+ldaf(x)dx=C∫
l取a=0C=f(x)dx0∫
∴∫aa+lf(x)dx=f(x)dx0∫l
第四节 理论应用
1.零点定理
2.介值定理
3.罗尔定理
4.拉格朗日中值定理
5.柯西中值定理
6.泰勒中值定理
7.积分中值定理
8.费马引理
【例1】1)设f(x)在区间[0,1]上连续,且f(0)=1,f(1)=0,试证明,0,1),使得f()=.ξ∈(ξξ证明 令F(x)=f(x)-x F(x)在[1,1]上连续 F(0)=f(0)-0=1
F(1)=f(1)-1=-1 F(0)·F(1)<0
由零点原理知
t(0,1)使F()=0ξξ
即f()=ξξ
2)设f(x)在区间[0,2a]上连续,且f(0)=f(2a),试证明,0,2a),使得f()=f(+a).ξ∈(ξξ证 令F(x)=f(x+a)-f(x)
F(0)=f(a)-f(0) F(a)=f(2a)-f(a)=f(0)-f(a)
2F(0)·F(a)=-(f(a)-f(0))
如果 f(a)=f(0)=f(2a)=f(a+a) 取ξ=a
2否则 F(0)·F(a)=-(f(a)-f(0))<0
F(x)满足零点原理 ξ0,a),F()=0 即 f(+a)=f()∈(ξξξ
32【例2】1)证明方程x-4x+1=0在区间(0,1)内至少有一个实根
—24—
《微积分》考点精讲
32证明 令f(x)=x-4x+1
f(0)=1 f(1)=-2
f(x)在[0,1]上满足零点原理
0,1) f()=0ξ∈(ξ
32即 x-4x+1=0在(0,1)内至少有一个根
2)讨论方程lnx=ax,(a>0)有几个实根
解 令f(x)=lnx-ax f(+∞)=-∞
1f′(x)-a f(0+0)=-∞x
11f″(x)2 x为最大值点ax
()
11当(x)有一个零点方程lnx=ax只有1个根 即a时 f(a)=0e
1(x)有两个零点方程lnx=ax有2个根当>0 即a时 f(1)ae
ππ)内根的个数.3)就k的不同取值情况,确定方程xsinx=k在开区间(022
πinx-k f(0)=-k 解 令f(x)=xs(2)=-k2当11(x)无零点方程lnx=ax无根<0 即a时 fae
2ππosx f″(x)sinx>0 x=arcco为最f′(x)=1c22π
π上无零点方程无根k(x)在0≥0时 f2
22π2当k<0时 f(arcco)=arccosinarcco-k>0ππ2π
2π2即 k<arccosinarcco 方程无根π2π
2π2k=arccosinarcco 方程只有一个根π2π
22k>arccosinarcco 方程有两个根π2π
【例3】 若函数f(x)在[a,b]上连续,a<xx…xb,则在区间[x,x]上至少有一点ξ,使1<2<n<1n
f(x)+f(x)+…+f(x)12n得f()ξn
证明 f(x)在[a,b]连续 f(x)在[x,x]连续f(x)在[x,x]有最大值M,最小值m1n1n
m(x)=1,2,…,n≤f≤M ii
(x)+f(x)+…+f(x)M+M+…+Mm+m+…+mf12n=Mm≤≤nnn
—25—()
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
由介值定理知x,x]<(a,b)使ξ∈[1n
)+f(x)+…+f(x)f(x12nf()ξn
【例4】 若函数f(x)在(a,b)内具有二阶导数,且f(x)=f(x)=f(x),其中a<xxxb,1231<2<3<证明至少存在一点ξa,b),使得f″()=0.∈(ξ
,x],[x,x]上分用罗尔定理证明 对f(x)在[x1223
x,x),x,x)ξ∈(ξ∈(112223
使f′()=0 f′()=0ξξ12
再对f′(x)在[,]上用罗尔定理ξξ12
,)<(a,b)使ξ∈(ξξ12
f″()=0ξ
2【例5】 设函数f(x)在区间[1,2]上二阶可导,且f(2)=f(1)=0,又F(x)=(x-1)f(x),那么
在区间(1,2)内至少存在一点ξ,使得F″()=0ξ
证明 ∵F(1)=0 F(2)=f(2)=0
∴F(x)在[1,2]上满足罗尔定理
1,2)使F′()=0η∈(η
2又 F′(x)=2(x-1)f(x)+(x-1)f(x) F′(1)=0
F′()=F′(1)η
F′(x)在[1,]上满足罗尔定理η
1,)使F″()=0ξ∈(ηξ
【例6】 设f(x)在区间[0,1]上连续,在(0,1)内可导f(1)=0.证明:在(0,1)内至少存在一点ξ,使f()+f′()=0如果将结论改为2f()+f′()=0ξξξξξξ
证明 令F(x)=xf(x) F(0)=0 F(1)=f(1)=0
F(x)在[0,1]上满足罗尔定理
0,1)F′()=0ξ∈(ξ
即f()+f′()=0ξξξ
a+b【例7】 f(x)[a,b],f(x)(a,b),f(a)·<0,f(a)f(b)>0证明:至少存在一个∈C∈D2
a,b)使得f′()=f()ξ∈(ξξ
a+ba+b证明 f(a)·<0 f(a)·f(b)>0 于是·f(b)<022
a+ba+bb上适用零值定理f(x)在a·22()()()[][]
a+ba+bb使, ξξ∈a∈1222
f()=f()=0ξξ12
-x令F(x)=ef(x)()()
—26—
《微积分》考点精讲
F()=F()=0ξξ12
,]上满足罗尔定理F(x)在[ξξ12
,)使F′()=0ξ∈(ξξξ12
)=f()即f′(ξξ
a,b),使得【例8】 f(x),g(x)在[a,b]上可微,g′(x)≠0证明至少存在一点ξ∈(
′()f)f(a)-f(ξξg()-g(b)g′()ξξ
证明 令F(x)=f(a)g(x)-f(x)g(x)+g(b)f(x)
F(a)=g(b)f(a)
F(b)=f(a)g(b)
F(a)=F(b) F(x)在[a,b]上满足罗尔定理
a,b)使F′()=0ξ∈(ξ
即)f′()f(a)-f(g(′()-g(b)g)ξξ
b
a【例9】 f(x)[a,b],f(x)(a,b),证明:至少存在一个ξa,b)使得f(b)-f(a)=l∈C∈D∈(
f′()·ξξ
证明 对f(x)、lnx在[a,b]上用柯西中值定理
′(f(b)-f(a)f)ba1lnln-
ξ
b即f(b)-f(a)=l·ξf′()ξa
【例10】 设函数f(x)在[-1,1]具有三阶连续导数,且f(-1)=0,f(1)=1,f′(0)=0证明:
1,1),使f()=3.ξ∈(-ξ
f″(0)2()3fη证明 f(x)=f(0)tf′(0)xx-x2!3!
()ξf″(0)f1f(-1)=f(0)…①32!!
()ξf″(0)f2f(1)=f(0)…②2!3!
f()+f()1ξξ121f() (介值定理)ξ63
得f()=3ξ
—27—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
第三章 一元函数积分学
第一节 不定积分
一、基本概念(原函数和不定积分的概念)
【例1】 若f(x)的导函数是sinx,则f(x)有一个原函数为(B)
A1+sinx B1-sinx C1+cosx D1-cosx【例2】 下列各式正确的是(C).Adf(x)dx=f(x)Cdf(x)dx=f(x)dx
∫
d
Bf(x)dx=f(x)+Cdx
∫
∫
dDf(x)dx=f(x)dxdx
二、求不定积分
1.利用积分表(1)0·dx=c;
+1α
x
+c;(3)xdx
α+1
∫
αx
(2)kdx=kx+c;(4)
∫∫
∫
α≠-1
1
;dx=l+c
x
x
(5)edx=e+c;(7)cosxdx=sinx+c;
2
ecxdx=tanx+c;(9)s
∫∫
x
x
a
+c;(6)adx=lna
∫
(8)sinxdx=-cosx+c;
2
(10)cscxdx=-cotx+c;
∫∫
(11)secxtanxdx=secx+c;(13)
∫∫
2
(12)cscxcotxdx=-cscx+c;(14)
x=arcsinx+c;-x∫
1
dx=arctanx+c;2
1+x
1
(15)tanxdx=-lncosx+c;
(17)secxdx=ln(secx+tanx)+c;(19)(21)
11x-a
x=l+c;2ax+ax-a
2
∫
(16)cotxdx=lnsinx+c;
(18)cscxdx=ln(cscx+cotx)+c(20)
11x
dx=arcta+caaa+x
2
2
∫
∫
x
x=arcsi+c;aa-x1
(22)—28—
x=ln(x+x±a)+cx±a1
《微积分》考点精讲
【例3】 求下列不定积分
1.1x22dx(1+x)
111d-arctanx+Cxxx+122解 原式=
2.1dx1+cos2x
111ecxdx=tanx+Cdx=s222cosx2
2解 原式=
3.1dxsinxcosx22
22sinx+cosx22ecx+cscxdx=tanx-cotx+ε解 原式=dx=s22sinxcosx∫
24.sin∫
∫xdx2xsinx1-cosxdx=+C222解 原式=
25.tanxdx
2解 原式=secx-1dx=tanx-x+C∫
2.凑微分法(第一换元法)
本例小结
【例4】 求下列不定积分
211sinx13x+1odx; (4)3dx; (2)1.(1)x; (3)2cdx;3dxcosxxx+x+21+x)1arcta2xx-2x(5)(x-1)edx; (6)x; (7)2d(1+x)∫
∫
ln(x++x)+5dx+x解 (1)(2)112arcta+Cdx=21+x)(1+2sinx1--3dx=-cosxdcosx=cos2x+C32cosx∫(3)11111codx=-co=-si+C2xxxxx∫233x+1132|x+x+2|(4)3dx=3d(x+x+2)=ln+Cx+x+2x+x+2x-2xx-1)edx=(5)(22221x1xx2-2xe-d(x-2x)=e+C22∫1arctax11112+C(6)dx=-arctadarctaarcta2xx2x1+x∫()
—29—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
=32+C(ln(x++x)+53
2342.(1)sinxdx; (2)sinxdx; (3)secxdx; (4)∫∫∫1sinxdx; (5)dx;1-cosx1+sinx(6)∫
∫
sinx1dx; (7)x22dsinx+cosxsinx+2cosx2inxdx=解 (1)s∫1-cos2x11x=xsin2x+C22413cosx-cosx+C332(2)sinxdx=-(1-cosx)dcosx=∫42(3)secxdx=(tanx+1)dtanx=∫13tanx+tanx+C3(4)1dx=1-cosxxdx=-co+C22x2sin21(5)sinxsinx(1-sinx)sinx2dx=anxdxdx=x-t22d1+sinxcoscosxx∫2ecx-1dx=sec-tanx+x+C=secx-s∫(6)sinx1sin+cosx-(cosx-sinx)dx=dxsinx+cosx2sinx+cosx=11xlnsinx+cos+C22
21secxtanx1(7)rcta+Cx=dx=22d2sinx+2tanx+2cosxxe11x; (2)x (3)xdx3.(1)xdxd-x1+e1+ee+exe1xx解 (1)dx=d(1+e)=ln(1+e)+Cxx1+e1+exx11+e-exx=x=x-ln(1+e)+C(2)xdxd1+e1+ex1ex(3)xdx=arctanedx=+C-xx2e+e(e)+14.xdx2x+x+1
解 2x12x+1-11(1x+x+1)lndx=dx=222x22x+x+1+x+1(1x123x42)
1x2x1(12+1)rcta+C=lnx+2/2—30—
《微积分》考点精讲
x-xx【例5】 1)已知f′(e)=xe,且f(1)=0,求f(e)
x2(x)dx=e+C,xf(1-x)dx=2)f∫
∫2∫3)f(x)dx=F(x)+C,x=at+b,f(t)dt=
AF(x)+C
1(at+b)+CCFa
xxxx解 (1)ef′(e)=x f′(e)edx=xdx∫BF(t)+CDF(at+b)+C∫∫
xf(e)=1212xx+C f(1)=0 ∴f(e)=xC=022
2211(221-x)f(1-x)d(1-x)e+C222(2)xf(1-x)d∫∫
(3)选“B”
【例6】 设F(x)是f(x)的一个原函数,F(x)>0,F(0)=1,当x>0时f(x)F(x)=cos2x求f(x)解 f(x)F(x)=cos2x
F′(x)=F(x)=cosx
∫121in2x+CF(x)F′(x)dx=cos2xdx(x)=s22∫
1(x)=F(0)=1 C F2
cos2xcos2xf(x))F(x3.第二换元法(三角代换,无理代换,倒代换等)
【例8】 (1)-xdx解 令x=asint 1+1≤
222原式=acostdt=aπ2∫cos2tdt1-
2
12t=asin2t+C24
22-xaπaxrcsi·+C=a222aa
2aπx=arcsi-x+C222()
(2)x+a1
解 x=atant ≤2
—31—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
原式=∫12asectdtasect
=sectdt
=ls+Cect+tan
=ln(x+x+a)+C
(3)dx-a1
解 令x=asect
原式=1asecttantdtatant
=ln|sect+tan-1|+C
-a)+C=ln(x+x
【例9】 (1)111dx; (2)dxx (3)1+(x+3)+e解 (1)令=t
11dx=·2dt=2arctan+C=2arctan+C2(t+1)(x+3)(2)令+e=tx=+e112t+e-+C=l-+C·2dt=lttt-1t++e+(3)令5216tt+1-1=3t=6t=6(t-arctant)+C22dt(1+t)1+t1+=6-arcta+C【例10】 1dxx(x+1)6解 原式 56x1xn6+Cdx=l666xx(x+1)+1()
4.分部积分法
【例8】 求下列不定积分
(2)xsinxdx;∫∫
解 (1)xedx=∫xde=xe-∫edx=(x-1)e+C∫
(2)xsinxdx=-∫xdcosx=-(xcosx-∫cosxdx)=-(xcosx-sinx)+C∫
2.(1)xlnxdx(2)arctanxdx(3)arcsinxdx∫∫∫x1.(1)xedxxxxxx2
—32—
《微积分》考点精讲
2222xxxxx解 (1)xlnxdx=lnx=lnx-dx=lnx+C22224∫∫rctanxdx=xarctanx-(2)a∫
∫x12dx=xarctanxl)+Cn(1+x221+x
22(3)arcsinxdx=xarcsinx-2∫xarcsinxx-x2=xarcsinx+2arcsinxd-x
2=xarcsinx+2(-xarcsinx-1dx)2x+2(-xarcsinx-x)+C=xarcsinx3.(1)esinxdx∫∫∫
解 (1)esinxdx=∫sinxde=sinx·e-∫ecosxdx=sinx·e-∫cosxde∫3(2)secxdxxxxxxx
xxx=esinx-ecosx-esinxdx∫
xsinxdx=∴e∫1xe(sinx-cosx)+C2
3(2)secxdx=secxdtanx=secxtanx-tanxsecxtanxdx∫∫∫
3ecx-secxdx=secxtanx-s∫
3∴secxdx=∫1secx+tanx+lns)+Cecx+tan2
(2)4.(1)xcosxx3sinxxxedx2(x+1)
解 (1)xcosx11-2-2-2dxdsin(xsinx-sinxdx)322sinx∫∫
1xotx+C2+c2sinx()
xxxe1xexx(2)dx=-xe=--edx2x+1x+1(x+1)∫(∫)
xxex=-+C-ex+1()
2x2(tanx+1)dx5.e∫
2x22x解 原式=esecx+e2tanxdx∫
2x2x2x=etanx-2etanxdx+e·2tanxdx
2x=etanx+C∫∫
—33—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
【例9】 设函数f(x)的一个原函数是sinx
x,求积分∫xf′(x)dx.
解 ∫xf′(x)dx=∫xdf(x)=xf(x)-∫f(x)dx
=x·(sinx
x)′sinx
x+C
=xcosx-sinxinx
xs
x+C
5.几类特殊类型函数的积分
(1)有理函数的积分
(2)三角函数的积分
(3)指数函数的积分
(4)简单无理函数的积分
(5)分段函数的积分
【例10】 ∫max(1,x2,x3)dx
≥1
解 max(1,x2,x3)={x3x1|x|≤1
x2x<-1
?1
?4x4+C1x≥1
∫max(1,x2,x3)dx=??x+C2≤1
???1
3x3+C3x<-1由原式数的连续性知
{1
4+C1=1+C2
C1
2-1=C33
令C2=C C1=C3
4 C3=C2
3
第二节 定积分
1.定积分的概念
(1)定积分的定义
【例1】 求下列极限
1.nl→i∞n
—34—
《微积分》考点精讲
1n!nnnim解 li=lnn→∞n→∞…+++)=eli(12n1
n→∞=es′lnxdx0
-1=e
【例2】 设f(x)是连续函数,且f(x)=x+2f(x)dx,求f(x)0∫1
解 令f(x)dx=k0∫1
f(x)=x+2k
1f(x)ax=∫x+2kdx=+2k=k∫20011
∴f(x)=x-1
2.定积分的性质
(1)区间可加性
(2)比较性质
(3)估值定理
(4)积分中值定理
3.重要公式12
1)若f(x)在[-a,a]上连续且为偶函数,则
f(x)dx=2∫f(x)dx;∫-a0aa
若f(x)在[-a,a]上连续且为奇函数,则
f(x)dx=0∫-aa
2)0a2aπ-xdx=43)设f(x)是以l为周期的连续函数,证明
∫aa+lf(x)dx=f(x)dx.0∫l
4)In=sinxdxcosxdx(=)=nn00ππ{n-1n-331π·…··,n为正偶数nn-2422n-1n-342·…·,n为大于1的正奇数nn-253
π5)xf(sinx)dx=20∫
∫0ππf(sinx)dx∫0πn6)sinxdx=2sinxdx0n—35—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
4.定积分的计算
(1)牛顿—莱布尼兹公式
【例5】 求下列积分1dx,1+x)1
41解 x=2arcta11+x)144
=2arctan24
(2)对称性【例6】 求下列积分
(1)(x+sinx)cosxdx322
ππ()
124解 原式=2sinxcosxdx=2sinx-sinxax=21·π31·π=π800224223
02222()(2)(xln(x++x)--x)dx∫2-33解 原式=2
(3)π99ππ--xdx=-2·∫4248(xarctanx+cosx+sinx)dx2
π48解 原式=2cosx+sinxdx02
=2·317531··+2·····42286422
83=π128
(4)∫-112f(x)(x+1)dx,,y,f(x+y)=f(x)+f(y)x
解 ∵f(x+y)=f(x)+f(y)
f(x-x)=f(x)+f(-x)=f(0)
f(0+0)=f(0)+f(0) f(0)=0
∴f(x)为奇函数
∴f(x)f(x+1)dx=0∫2
-11
x++x(5)-xldx,-121解 原式=-x(lnx++x-ln2)dx-11
=-2ln2-xdx01
—36—
《微积分》考点精讲
ln22
(3)换元法
2sinxdx【例7】 (1)π-x1+e解 令t=-x
2sinx设A=πdx=-x1+eπ2sintdttπ1+eπxe12A=πsinxdx=xx1+e1+e(24)1-cos2xπ1sinxdx=2dx=2(284)2
π440
∴A=1π184xrctanedx,(2)a-1∫
1
-1解 令t=-xA=∫
1xarctanedx=arctanedt∫-t-112A=
A=dx=ππ2-1π
2
【例8】 (1)
解 令t=设A=
2A=
A=(2)02012sinxx20122012dsinx+cosxπ-x20π2012sinxx=20122012dsinx+cosx0π2012costt20122012dcost+sintπdx=202π40
π1dxα1+tanxπ-x2解 令t=A=0
π1dx=α1+tanx0π1dtα1+cott2A=
A=dx=20π
4
—37—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
【例9】 (1)
0
π
xsinx
x2d1+cosx
2π
inxππsππ
rctancos解 原式=a=2d201+c24osx0
∫
4
(2)xsinxdx
0
∫
π
2231π3ππ4π4解 原式=sinxdx=πsinxdx=π···=
02042216
【例10】
ln(1+tanx)dx0
π
解 令t=
π
-x4
4
1-tantdA=lt=lt=ln(1+tanx)dx=ln1+tanπ-tdn1n2-ln(1+tant)dt
00004t1+tan
4
[
4
()][
4
]
2A=A=
ln24
πln28
(4)分部积分法【例12】 (1)
0
1
ln(1+x)
x2d(2-x)
11
111ln(1+π=·dx解 原式=ln(1+x)-
02-x2-x002-xx+1
∫
1
1x-=ln2l3x+(cosx-sinx)
(2)x
10
21
=ln2ln2=ln2
33
π
x
解 原式=
=
x-πxxπxπsinx
dx=π
ππ
x
d+2πππx
+)(-dx=ππ
2
【例13】 f(2)=1,f′(2)=0,f(x)dx=1,xf″(2x)dx=
0
0
1
∫
2
∫
1
2解 xf″(2x)dx
0
111
1122=xf′(2x)dx)xdf′(2x)=(xf′(2x-2
02020
∫
1
∫∫
111
11=x(2x)dx)f′(2x)dx=xdf(2x)=(xf(2x-f
002020
∫∫
111
=f(2x)dx220
∫
—38—
《微积分》考点精讲
112=f(u)du240∫
=1
4
2x【例14】f(x)dx,其中f(x)=1)计算x0∫11sintdtt
22xx解 xf(x)dx=f(x)=·0022∫1∫1inxsint1-1x·sxdxd2·2021tx02x222=1cosx210=
2)计算积分
解 π1(cos1-1)2xπsintf(x)dx,其中f(x)=dt∫t0π
∫0πf(x)dx=xf(x-x·0
0∫πsinxxx
=-sinxdx0∫π
=-2
(5)分段函数的积分
【例15】
21)max(x,x)dx-22∫
解 原式=
=xdx+∫xdx+∫xdx∫22-201012817323
11=2
2)设f(x)={≤0x+1-1≤x
x0<x≤1,F(x)=
xf(t)dt,x-1,1]的表达式.∈[∫-1xx解 当-1≤x(x)=≤0时 F
0<x F(x)=≤1x∫-1f(t)dt=∫-1t+1dt=12(x+1)2f(t)dt=∫1+tdt+∫tdt∫-1-100x
=112x22
3)设f(x)={-xxe,2x≥0(x-2)dx,计算f11,-1<x<01+cosx
—39—∫4
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
解 令x-2=t f(x-2)dx=
1
∫
4
f(t)dt∫
-10
2
2
21-tedt=dt+t
-11+c0ost
∫
20
0
2t-t
=ta1e
2-21
11-4
=ta(1-e)
22
(6)含绝对值的积分【例16】
x; (2)x(1)1l-4x+4dx; (3)tndd-20
π0
e
5
1
(4)
x (5)x0
π
(1)解
2
-lnxdx+∫lnxdx=2x=lnde
1
1eee
1
(2)解
25
x+4dx=x-2)dx=∫2-xdx+∫x-2dx=-42
-21
-2
-2
2
5525
(3)解 txd0
2
当t-xdx=t≥1时 原式=tt
0
∫∫
01
1
t
2
x-t)dx=当t≤0时 原式=t(当0<t<1时 原式=(4)解
π
t2
-t2
(∫
0π0
t
t-xdx+x-tdx=t-tt
∫
1
)
32
t
2
x=0
πxxxxxxdx=co-sidx+si-codxsi-co0222222=4-4(5)解
0-x
π
x=0
π
cosxdx=0
osxdx+-osxdx=2π
(7)广义积分【例17】(1)(4)
edx (2)∫x∫
0
0
+∞
+∞
-x+∞
xe1
dxdx (3)-x222
0(1+e)(x+1)(x+4)
∫
-∞
+∞
++∞∞
111
dx (6)dx (5)dx22α00(x(x+4x+9)+1)(1+x)1+x)∫∫
(1)解
edx=-(x+1)e∫x
-x
0+∞
-x
+∞
+∞
+∞-x
0
=1
x
(2)解
xexe
dx=∫dx=(x-ln∫(1+e)(1+e)
0
-x2
0
x2
x(1+e)
x
x1+e
)
+∞
=ln2
0
—40—
《微积分》考点精讲
(3)解
∫
0
+∞
∞
11+11
dxdx=2222
30x+1x+4(x+1)(x+4)
∫()
11x=arctanxrcta322
()
+∞
0
π=12
(4)解
∫
-∞
+∞
1
x=2
x+4x+9
-∞
0
+∞
11
dx+dx22
0(x+2)+5(x+2)+5
∞
x+0x++11
=rctarcta0-∞=π5
(5)解 (6)解 令u=
0
+∞
+∞
1
dx=2arctan=π1+x)0∫
0
+∞
1
dx 令x=tant 原式=2α
(x+1)(1+x)1
dt1+tant
0
α
π
π
-t2
0
π1
dt=α
1+tant
0
π
1111
u=dtααα
201+t1+cotuant1+cott
π
1π
=dt=204
π
【例18】(1)
xxx-1
-2
-1
1
解
-2
-1
x=xx-1
1
-2
-1
1
2
-x
12
x
1
x=arcsix-1
-2
π
3
(2)
1
dxx(1-lnx)
2
4
4
11
解 原式=dx+x
2xex(1-lnx(1-lnx))
e
e4
=-ln1-ln2
+(-l1-lne
发散
(8)定积分不等式的证明
【例19】 设f(x),g(x)在区间[a,b]上连续,证明柯西不等式:f(x)g(x)dx[∫]
ab
2
b
b
≤
f(x)dxg(x)dx∫∫
2
2
a
a
x
222
证明 令F(x)=f(t)dtg(t)dt-(f(t)g(t)dt)
a
a
a
∫∫
x
∫
x
—41—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
F(a)=0
F′(x)=f(x)g(t)dt+g(x)f(t)dt-2f(x)g(x)f(t)g(t)dtaaa
2=(f(x)g(t)-f(t)g(x))dt≥0a2∫x22∫2x∫x∫
b4∴F(x)≥0 取x=b即可得f(x)g(x)dx(∫)a2≤f(x)dxg(x)dx∫∫22aabb
【例20】 设f(x)在[0,1]可导,f(0)=0,0<f′(x).≤1
试证:f(x)dx(∫)012≥f(x)dx∫30
x3(t)dtf(t)at-0f21证明 令F(x)=
F(0)=0(∫)0∫x
3F′(x)=2f(x)f(t)dt-f(x)0∫
x
0x2=f(x)2f(t)dt-f(x)
x(∫)3f(0)=0 f′(x)>0 ∴f(x)>0 令φ(x)=2f(t)dt-f(x)0∫
(0)=0φ
′(x)=2f(x)-2f(x)f′(x)φ
=2f(x)(1-f′(x))>0
∴F′(x)>0 可得F(x)>0
取x=1有
f(x)dx(∫)012≥f(x)dx∫301
a+b【例21】 设f(x)在区间[a,b]上有二阶导数,且=0,证明:2()
∫3M(b-a),其中M=max{f″(x)}f(x)d≤xa,b]∈[24ab
证明 设F(x)=f(t)dta∫x
Fa+b
2()ξa+b2Fa+b3F(x)=Fa+b+Fa+bxa+bxx2!3!22222(
())(()())()()()Fa+b
23F()(ξb-a2(b-a)b-a)1a+ba+bF(b)=F+F2!4!82322
Fa+b
23F()(ξa-b2(b-a)a-b)2a+ba+b+FF(a)=F22!43!822()()()()
—42—
《微积分》考点精讲
3)+f″()f″(ξξ(b-a)12F(b)-F(a)=f(x)dx=a38!∫b
∫33(b-a)f″()+f″(M(b-a)ξξ12≤f(x)d=2424a2b
5.积分的应用
(1)定积分的微元法
(2)几何应用a)平面图形面积直角坐标,参数方程和极坐标
b)旋转体体积
c)平面曲线的弧长直角坐标,参数方程和极坐标
【例22】 求由曲线y=lnx与两直线y=e+1-x及y=0所围成的平面图形的面积
y+1-y-edy=解 面积为e0∫
a132【例23】 求下列曲线所围图形的面积33(1)x=acost,y=asint解 面积为4ydx=43asintcostdt=12a00
2∫sint(1-sint)dt=12a(3·1·π5·3·1·π)42264222422042
=32aπ8
2π(2)摆线x=a(t-sint),y=a(1-cost)的一拱与横轴解 面积为A=dx=∫a(1-cost)dt∫y22
002aπ
2=a(1-2cost+cost)dt∫2
02π
2a=3π
2【例24】 (1)求双扭线ρ=2cos2所围成区域的面积θ
解 A=40
ππ412d=22cos2d=2sin2θθθ=2020π2(2)求ρin2,=os所围成区域的面积θρθ解 A==011in2)d+os)dθθθθπ22ππ (0≤x)≤π6
π【例25】 求曲线y=sinx与x轴所围图形分别绕x轴,y轴,y=1旋转所成立体体积.πsinxdx=2inxdx=解 Vππsx=002∫π222
ππ2V2xsinxdx=2·sinxdx=2πππy=020∫π∫
绕y=1旋转的体积
—43—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
V=∫ππ12dx-∫π
0π(1-sinx20)dx
=π2-(π22
-4ππ2)
2
=4ππ2
【例26】 过原点作曲线y=lnx的切线,
(1)求切线,曲线及x轴所围图形的面积
解 设切点为(x0,lnx0)
lnx0-0
x1 x
0-0x0=e
0
切线为yx
e
面积为∫1
0ey-eydy=e2-1
(2)求此图形绕直线x=e旋转一周所成立体体积解 体积为V=11
3πe2-∫0π(e-ey)2dy=52π
6πe-2πe2
—44—
《微积分》考点精讲
第四章 多元函数微分学
一、二元函数
1、二元函数的解析式
2xy,求f(x,f(x,x))【例1】 设f(x,y)x+y
22xxx解 f(x,x)x+x2
2xx·2x2f(x,f(x,x))=fx22xx2()
2x22+x
y22【例2】 设f(x+y)=x-y,求f(x,y)x
解 令u=x+y
vy
x
22u2uv2u(1-v)f(u,v)=-21+1+vv(1+v)()()
22(1-y)x∴f(x,y)2(1+y)
2、二元函数的极限
xy22y≠02x+x+y,讨论P(x,y)【例3】 设f(x,y)=(0,0)时函数极限→O2{
022+y=0x
解 取y=kx
2xykxklim22=lim3222x0x+→0x+yxkx1+ky=kx
其极限随k变化而不同
∴limxy不存在2x→0x+yy→02
2yx22y≠042x+x+y,讨论P(x,y)(0,0)时函数极限【例4】 设f(x,y)=→O{
022x+y=0
2解 取y=kx
—45—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
2
lxiy=→mxykx4k0kx2x4+y2=lxi→m0x4+k2x41+k2随k变化而不同
2
∴lximxy42不存在
y→0→0x+y
【例5】lxix+yy→0→0-1
解 令x+y=u
原式=limu
u→0=lu=2-1ui→m01
2【例6】 (1)lxim(x2+y2)si1y→0→0x2+y2
解 原式=0(无穷小与有界量之积)
(2)lx3+y3
xiy→0→0x2+y2
解 lx3+y3x2
xi22=l
y→0xim22xy222·y=0
→0x+yy→0→0(x+yx+y)
【例7】 (1)lxyxiy→0x+y→0
x2+y2
解 0≤x2+yx+y+y2
而lxi+y=0y→0→02
∴lixy
xy→0→0+=0y
(2)lim(x2+y2)2x2y2
xy→0→0
解 原式=l2x2y2ln(x2+y2)
ximey→0→0
(20≤xn(x2+y≤x+y2)22y2l2
2ln(x2+y2而lui→m40ulnu=0
∴lxi(x2+y2)2ln(x2+y2=0y→0→04
∴lim(x2+y2)2x2y2
x=1y→0→0
3、二元函数连续;偏导存在;可微的讨论
(1)函数在(x0,y0)处连续lx→imxf(x,y)=f(x0,y0)
y→y0
0
(2)函数在(x0,y0)处的偏导
—46—
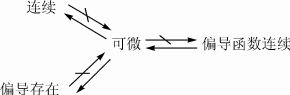
f′f(x0+Δx,y0)-f(x,y)x(x0,y0)=00
Δlix→0Δx
或
f′f(x,y0)-f(x,y)
x(x0,y0)=l00
x→ix0x-x0
(3).函数在(x0,y0)处可微
Δlif(x0+Δx,y0+Δy)-f(x0,y0)-f′x(x0,y0)Δx-f′y(x0,y0)Δy=0Δxy→0→0x+Δy
xy22
【例8】 设f(x,y)={x2+y2,x+y≠0试问该函数在点(0,0)处
0,x2+y2=0
(1)是否连续?(2)偏导数是否存在?
解 f(x,y)在(0,0)处不连续 ∵lxy
xiy→0→0x2+y2不存在
f′f(x,0)-f(0,0)0-
x(0,0)=lxi→0x-0=lxi→00x-0=0
同理 f′y(0,0)=0
【例9】 设f(x,y)={xyx+yx2+y2≠0试问该函数在点(0,0)处
0,x2+y2=0
(1)是否连续?(2)偏导数是否存在?(3)是否可微?
解 lxy
xiy→0→0+=0=f(0,0)y
∴f(x,y)在(0,0)处连续
(2)f′f(x,0)-f(0,0)
x(0,0)=lxi→0x-0=lxi→0-00x-0=0
同理f′y(0,0)=0
(3)f(0+Δx,0+Δy)-f(0,0)-f′x(0,0)Δx-f′y(0,0)xyΔliΔxy→0→0Δx+Δy
xy
=lΔiΔxx+Δy y→0=lΔxΔy
→0x+ΔyΔiΔxy→0→0Δ2+Δ2y不存在
∴f(x,y)在(0,0)处不可微
—47—《微积分》考点精讲
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
12222(x+y)si22 x+y≠0x+y,试问该函数在点(0,0)处【例10】 设函数f(x,y)=
022+y=0 x{
(1)是否连续?(2)偏导数是否存在?(3)是否可微?
122(x+y)si22=0=f(0,0)解 limx→0x+yy→0
∴f(x,y)在(0,0)处连续
12xsi2-0f(x,0)-f(0,0)x=li=0(2)f′(0,0)=lixxx-0-0xx→0→0
同理 f′(0,0)=0y
122(+)si2x-0y0ΔxΔyΔΔ2-1+ΔxΔy=limx+ysi20(3)liΔΔ2=xxΔΔ→0→0x+yΔΔ+ΔxΔyyyΔΔ→0→0∴f(x,y)在(0,0)处可微
33xy-xy22 x+y≠022,x+y【例11】 设f(x,y)=(0,0);f″(0,0) 求f″xyyx{
0,22x+y=0
f(x,0)-f(0,0)解 f′(0,0)=li=0xxx-0→0
33y-xyx 22 f(x,y)-f(0,y)x+y=li=-yf′(0,y)=lixxxx-0x→0→0
f′(0,y)-f′(0,0)-yxx=li=-1f″=lixyyyy-0→0→0y
同理f″(0,0)=1yx
二、求偏导
1.具体的复合函数求偏导
y【例12】 (1)设u=x,求
zuzy=yx-1
xzuuuxyz解
zuyz-1=xlnx·zyy
zzuy=xylnyz
222rrr2(2)设r=x+y+z,证明222=rxyzrxryrzxyz+y+z+y+zy+z+
—48—
zx2
2rx+y+x+y+zx2x2+y2+z2
2r+y+zy2
y2x+y+zx2+y2+z2
r2+y+zz2rz2x2+y2+y+z+z2
x+y2+z2
2r2r23+y+z2+y+zxr
2y2z2x2+y2+22zr(3)z=-x-y求+zx+zy
解 z-x
xa-x-yzy-y
-x-y+za
x+zy-x-y2.抽象的复合函数求偏导
【例13】
(1)设z=f(xyxy2z
y)+gx,其中f,g有连续二阶偏导数,求xy
解 z
x=yf′1
1yf′2yyx2g(x)
2z
xy=f′x11
1+y(xf1″1y2f1″2)y2f′2y(xfx
2″1y2f2″2)
1yy(y
x2g(x)x3gx)
(2)z=yz
f(x2-y2),求x
z2xyf′(2-y2)xx
f2(x2-y2)
(3)设u=f(x,xy,xyz)且f具有二阶连续偏导数,求u2u
xxz
u
x=f′1+yf′2+yzf′3
2u
xz=f1″1·0+f1″2·0+xyf1″3+y(f2″3·xy)+yf′3+yzf3″3·xy
=xyf1″3+xy2f2″3+yf′3+xy2zf3″3
—49—《微积分》考点精讲
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
(4)设函数z=f(x,y)在点(1,1)处可微,且f(1,1)=1=2=3,(1,1)(1,1)
3(x)=f(x,f(x,x)),求dφxφ(dxx=1
3x)dφ(2=3解 x)·φ′(x)φ(ax
′(x)=f′(x,f(x,x))+f′(x,f(x,x))·(f′(x,x)+f′(x,x))φ1212
′(1)=2+3(2+3)φ
=17
3dxφ(∴=51dxx=1
3.隐函数求偏导
【例14】
2z(1)设e-xyz=0,求 2xz
z解 令F(x,y,z)=e-xyz
zyz Fxz Fe-xyFx=-y=-z=
FFzzyzxzxyz zxFyFxyxyze-ze-
zzzze--y)(xy)-yz(exxz
2z2(ex-xy)2
yz2zz-yz(e-y)yze-xyz2(e-xy)
zzy(x)其中F(u),(x)均有连续偏导数,确定z=zz求证+=z.(2)已知Fx=0,y,v,yxyzz()
证:对Fy)=0两边对x求导.(x
zz
zz?z?--??xx?+?=F′·?F′·?012????22?z??z?
zF′z1xxF′+yF′12
对F(xy=0两边对y求偏导zz)
zz?-?z?-?xy?+??=F′·?F′012????22?Z??z?
zF′z2yxF′+yF′12
—50—
《微积分》考点精讲
xF′+zyF′zzz12+=zxyxF′+yF′12
duφ2y(3)u=f(x,y,z),(x,e,z)=0,y=sinx≠0,求φzdx
解 dzdu=f′f′cosx+f′·1+23dxdx
2sinx对φ(x,e,z)=0两边对x求导.
dzsinx′cosxe′φ′=02xφφ1+2dx3
sinx-2x′cosxe′φφdu1-2=f′f′cosx+f′·1+23dx′φ3()
4.求全微分
22【例15】 求函数z=ln(1+x+y),当x=1,y=2时的全微分
解 z2x22x1+x+y
2yz2y1+x+y
12dzdxdy33
三、多元微分学的应用
求极值
222【例16】 设z=z(x,y)是由x-6xy+10y-2yz-z+18=0确定的函数,求
z=z(x,y)的极值点和极值
解 略
22【例17】 椭圆x+4y=4上求一点,使其到直线2x+3y-6=0的距离最短
|2x+3y-6|解 d(x,y)222)=(2x+3y-6)+(x+4y-4)令L(x,y,λλ
′6(2x+3y-6)+8y=0令Lλy=
22x+4y=4{L′4(2x+3y-6)+2x=0λx=
解出(x,y),即可找到极值点.
【例18】 已知函数z=f(x,y)的全微分dz=2xdx-2ydy,并且f(1,1)=2,求f(x,y)在椭圆
2y域D={(x,y)|x≤1}上的最大值和最小值42
解 ∵dz=2xdx-2ydy
22z=x-y+C
—51—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
∵f(1,1)=2
∴C=2 于是f(x,y)=x2-y2+2
f′x=2x f′y=-2y
{x=0
y=0为驻点
令L(x,y,λ)=x2-y2+2+λ(x2y2
4-1)
?L′x=2x-2λx=0
?
令??L′λ
y=-2y2y=0
???x2y2
4=1
可得 (0,2) (0,-2) (1,0) (-1,0)
∴最大值为3 最小值为-2.
—52—
《微积分》考点精讲
第五章 二重积分
一、二重积分f(x,y)dσD
1.二重积分的定义
2.二重积分的几何意义和物理意义
若f(x,y)二重积分f(x,y)d=f(x,y)为顶,以D为底,侧面是以D的边界曲线≥0,σ表示以z
D
为准线,母线平行与z轴的柱面的曲顶柱体的体积.若f(x,y)≥0,二重积分
上占有区域D的,面密度为f(x,y)的平面薄片的质量.
222【例1】 已知D:x+y求I=≤a,f(x,y)dσ表示在平面D-x-ydσD
解 用几何定义有
Da-x-ydaσ=π323
3.二重积分的性质
(1)d其中σ为区域D的面积,据此可求平面图形的面积σ=σ,
D
(2)比较性质
若f(x,y)≤g(x,y),(x,y)∈D,则
特别的f(x,y)dg(x,y)dσ≤σDDσf(x,y)df(x,ydσ≤DD
推论:f(x,y)在D上非负连续,若f(x,y)d则f(x,y)=0σ=0,D
(3)估值性质设M和m分别是f(x,y)在闭区域D上最大值和最小值,其中σ为区域D的面积,则有mσ≤f(x,y)dσ≤MσD
(4)中值定理设函数f(x,y)在闭区域D上连续,其中σ为区域D的面积,则在D上至少存在一点(,),使ξηf(x,y)d(,)·σσ=fξηD
(5)二重积分的计算
1)利用直角坐标计算二重积分f(x,y)df(x,y)dxdyσ=DD
a)若区域D是X型区域,则D可以用不等式{(x)≤y(x)φ≤φ12来表示,则
a≤x≤b
(x)φ2
(x)φ1Df(x,y)dxdy=dxa(x,y)dy∫∫fb
—53—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
(y)≤x(y)ψ≤ψ12来表示,则b)若区域D是Y型区域,则D可以用不等式
c≤y≤d{
Df(x,y)dxdy=dyc(x,y)dx∫∫f(y)ψ1d(y)ψ2
c)若区域D即不是X型区域,也不是Y型区域,则用分块可加性,将D分成若干个X型区域和Y型区域上的积分之和.
【例2】 计算下列二重积分
222I=(x+y)d其中D为y=x,y=0,x=1所围平面区域σ,
D
12x
D2622解 原式=dx(x+y)dy=01050∫∫
∫0222d其中D:x+y=8,y=0,y=1,y=2x所围成平面区域I=xσ,yy解 原式=d21-y457xdx120
-yI=ed其中D:y=x,y=1,x=0所围成平面区域σ,
D
12
21-y解 原式=dyedx=yedye00020∫∫1y2-y∫12-y
-11-e2
2)利用极坐标计算二重积分
a)若积分区域可用不等式
则f(x,y)df(rcos,rsin)rdrdσ=θθθDD{
{()≤r()φθ≤φθ12来描述,α≤θ≤ββ()φ2θ
()φ1θαf(rcos,rsin)rdrdd(rcos,rsin)rdrθθθ=∫θθθ∫fD
(r)≤θ(r)φ≤φ12b)若积分区域可用不等式来描述,
a≤r≤b
则f(rcos,rsin)rdrddr(rcos,rsin)rdθθθ=∫θθθ∫f
Da(r)φ1b(r)φ2
222222【例3】 I=(x+y)d其中D为aσ,≤x+y≤b所围平面区域
D
b
a解 I=πddb-a)θρρρ=(∫∫2244
02π
【例4】 计算I=解 I=π-x-yd其中D:x+y=Rx所围成平面区域σ,22D∫0dθRcosθ022-ρdρρ=Rπ69()
—54—
《微积分》考点精讲
3)利用对称性计算二重积分
i.D关于x轴对称,D则≥0,1表示D的y
a)如果f(x,-y)=-f(x,y),则
b)如果f(x,-y)=f(x,y),则f(x,y)dσ=0Df(x,y)df(x,y)dσ=2σDD1
ii.D关于y轴对称,D则≥0,1表示D的x
a)如果f(-x,y)=-f(x,y),则
b)如果f(-x,y)=f(x,y),则f(x,y)dσ=0DD1f(x,y)df(x,y)dσ=2σD
【例5】 设D是xOy平面上以(1,1),(-1,1)和(-1,-1)为顶点的三角形区域,D1是D的第一象限部分,则(xy+cosxsiny)dxdy等于D
A.2cosxsinydxdy B.2xydxdy C.4(xy+cosxsiny)dxdy D.0D1D1D1
答:选A.
2x+y22【例6】 计算I=(x+xye)d其中a)D:x+yb)D为y=x,y=-1,x=1所围σ,≤1,
D22
成平面区域
解 a)原式=
b)原式=12xdσ2D1
-122x+y≤12122x-cydσ2132-1∫∫02π1π2ddθρρρ042xddxxdy=∫x+xdxσ=∫∫32
D-1x
3【例7】 设f(t)为连续函数,D为y=x,y=1,x=-1所围成平面区域,计算
22[1+yf(x+y)]dI=xσ
D
12dx3xdy-1x51解 I=Dxdσ=∫∫
2222222【例8】 I=(x+y)dxdy,D:x+yI=(x+y)dxdy≤R,
DD
(x+y+1)dxdy2
Dxdxdy2D
22xy22)dxdyabD解 πx+ydxdy=∫ddRθρρρ∫2222D002222πR4(x+y+1)dx+y+1+2x+2y+2xydσ=σDD
=D22x+y+1dσ=π42222x+ydRR+Rσ+ππ2D
—55—
考试点(www.kaoshidian.com)名师精品课程 电话:4006885365
14222xdxdyx+ydσR2D4D
22x111ydσ22222abab()11π4111π422RRx+yd=σ2222224abab()()DD
【例9】 D:(x-1)2+(y-1)2≤1,(x+y+1)dxdy=
D
解 xdσ=x·s(D)=π
D
同理 ydσ=π
D
x+y+1dσ=π+π+1dσ=3π
DD
6.二重积分中的题型
1)交换积分次序
【例10】 计算二次积分I=∫2
1dxxiπx42dy+dxiπx2y∫2dy2y
解 原式=∫2y2
1dy∫siπxdσy2y
【例11】 交换二次积分的积分次序:∫0
-1dx∫1-x2f(x,y)dy
01-y02解 ∫-1dx∫2f(x·y)dy=∫1dx∫1-x-f(x,y)dy
∫20=1dy∫1-y-f(x,y)dx
=∫21-y
1dy∫0f(x,y)dx
22【例12】 计算∫0dx∫xe-y2dy
2y解 交换积分次序得原式=∫0dy∫e-y20dx=∫20ye-y2dy
2
=1-y2
2e
0
1-
21-e4)
11【例13】 计算∫0dyx-ydx
解 交换积分次序
1x原式=∫dxx-y1dy=πx2
0004dxπ
12
2)直极相互转化【例14】 将下列极标下的二次积分化为直标下的二次积分π∫secθ
0dθ0f(ρcosθ,ρsinθ)ρdρ—56—
《微积分》考点精讲
解 原式=
∫∫001dxf(x,y)dyxdsindθθρ=∫ρ002cosθ
解 原式=dx∫002x-xyyx+y3)分段函数的二重积分
max{x,y}【例15】 计算I=edxdy,其中D={(x,y)|0≤x,0≤y}≤1
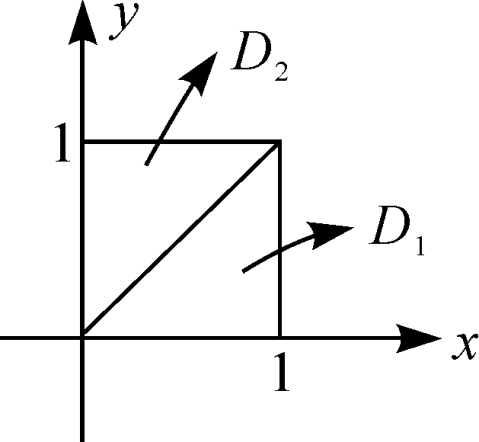
≤1
D
222解 原式==D11
0xedxdy+x2Dyedxdy1y2∫∫0
Dxdxedy+∫∫00ydyedx2=e-12222【例16】 计算I=(|x+y-4|)dxdy,其中D={(x,y)|x+y}≤9
2解 原式=
=22x+y≤4y-4dσ+x+σ4-x-yd222224+y≤x≤9∫∫002πd4-dθ(ρ)ρφ+22∫∫022π2d4)dθ(ρ-ρρ3
41π2
22【例17】 计算I=xy[x+y+1]dxdy,其中
D
222222D={(x,y)|x+yx,y},[x+y+1]表示不超过x+y+1的最大整数.≤≥0≥0
解 原式=∫00πdcosv·esind+θeθρρ13dcossindθ2ρθρθρρ108π6.二重积分的应用
1).空间曲面的面积
设曲面S由方程z=f(x,y)给出,D为曲面S在xOy面上的投影区域,函数f(x,y)在D上具有一阶连续偏导数,则曲面面积A=2).平面薄片的质心
设平面薄片占有xOy平面上的闭区域D,在点(x,y)处面密度为ρ(x,y),假定ρ(x,y)在D上连
x(x,y)dy(x,y)dρσρσ续,则薄片的重心坐标为,x=,y=
(x,y)d(x,y)dρσρσDD
DD1+)+)dσxy22D
特别地,若ρ(x,y)为常数,则平面图形的形心坐标为x=
其中A为D的面积.
—57—11xd,y=ydσσ,ADAD
-
高等数学微积分总结
积分整个高数课本,我们一共学习了不定积分,定积分,重积分(二重,三重),曲线积分(两类),曲面积分(两类).在此,我们对积分总结,…
-
高等数学微积分总结
积分整个高数课本,我们一共学习了不定积分,定积分,重积分(二重,三重),曲线积分(两类),曲面积分(两类).在此,我们对积分总结,…
-
微积分题型总结
微积分题型总结第一部分函数函数是整个高等数学研究的主要对象因而成为考核的对象之一特别是一元函数的定义和性质其中包括反函数复合函数隐…
-
微积分知识点小结
第一章函数一、本章提要基本概念函数,定义域,单调性,奇偶性,有界性,周期性,分段函数,反函数,复合函数,基本初等函数,初等函数第二…
-
微积分学习总结
第一章函数一、本章提要基本概念函数,定义域,单调性,奇偶性,有界性,周期性,分段函数,反函数,复合函数,基本初等函数,初等函数第二…
-
高等数学微积分总结
积分整个高数课本,我们一共学习了不定积分,定积分,重积分(二重,三重),曲线积分(两类),曲面积分(两类).在此,我们对积分总结,…
-
浙江大学微积分2方法总结
第七章矢量代数与空间解析几何★类型(一)向量的运算???222解题策略1.a?a?a,2.a?{a1,a2,a3},|a|?a1?…
-
高等数学微积分总结
积分整个高数课本,我们一共学习了不定积分,定积分,重积分(二重,三重),曲线积分(两类),曲面积分(两类).在此,我们对积分总结,…
-
微积分1方法总结
第一章函数极限连续注表示方法常用重要一求函数极限的方法1极限的四则运算2等价量替换3变量代换4洛比达法则5重要极限6初等函数的连续…
-
微积分题型总结
微积分题型总结第一部分函数函数是整个高等数学研究的主要对象因而成为考核的对象之一特别是一元函数的定义和性质其中包括反函数复合函数隐…
-
微积分学习心得
微积分学习心得学号11120472姓名吴心怡班级七班学号11120471姓名吴亚男班级七班时间,如同轨道上疾驰的列车,匆匆行驶,不…