拉伸法测金属丝杨氏模量的示范报告
拉伸法测金属丝杨氏模量的示范报告
一、实验目的
1.学会用伸长法测量金属丝的杨氏模量;
2.掌握光杠杆法测量微小伸长量的原理;
3.学会用逐差法处理实验数据;
4.学会不确定的计算方法,结果的正确表达;
5.学会实验报告的正确书写。
二、实验仪器
YWC-1杨氏弹性模量测量仪(包括望远镜、测量架、光杠杆、标尺、砝码)、钢卷尺、游标卡尺、螺旋测微器
三、实验原理
在外力作用下,固体所发生的形状变化成为形变。它可分为弹性形变和塑性形变两种。本实验中,只研究金属丝弹性形变,为此,应当控制外力的大小,以保证外力去掉后,物体能恢复原状。
最简单的形变是金属丝受到外力后的伸长和缩短。金属丝长 ,截面积为
,截面积为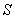 ,沿长度方向施力
,沿长度方向施力 后,物体的伸长
后,物体的伸长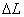 ,则在金属丝的弹性限度内,有:
,则在金属丝的弹性限度内,有:
我们把 称为杨氏弹性模量。
称为杨氏弹性模量。
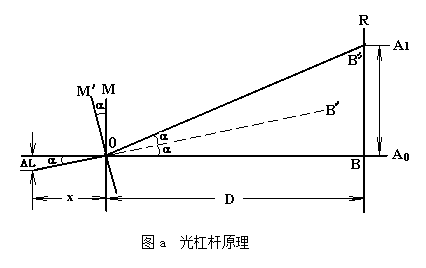
如上图:
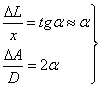
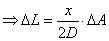 (
(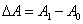 )
)
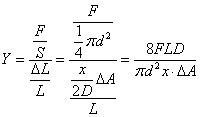
多次测量:
四、实验步聚:
(一)仪器调整
1、杨氏弹性模量测定仪底座调节水平;
2、平面镜镜面放置与测定仪平面垂直;
3、将望远镜放置在平面镜正前方1.5-2.0m左右位置上;
4、粗调望远镜:将镜面中心、标尺零点、望远镜调节等高,望远镜上的缺口、准星对准平面镜中心,并能在望远镜外看到尺子的像;
5、调节物镜焦距能看到尺子清晰的像,调节目镜焦距能清晰的看到叉丝;
6、调节叉丝在标尺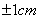 以内,并使得视差不超过半格。
以内,并使得视差不超过半格。
(二)测量
1、计下无挂物时刻度尺的读数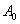 ;
;
2、依次挂上 的砝码,七次,计下
的砝码,七次,计下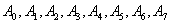 ;
;
3、依次取下 的砝码,七次,计下
的砝码,七次,计下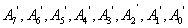 ;
;
4、用米尺测量出金属丝的长度 (两卡口之间的金属丝)、镜面到尺子的距离
(两卡口之间的金属丝)、镜面到尺子的距离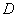 ;
;
5、用游标卡尺测量出光杠杆 、用螺旋测微器测量出金属丝直径
、用螺旋测微器测量出金属丝直径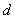 。
。
(三)数据处理方法——逐差法
1、实验测量时,多次测量的算术平均值最接近于真值。但是简单的求一下平均还是不能达到最好的效果,我们多采用逐差法来处理这些数据。
2、逐差法采用隔项逐差:
 注:上式中的
注:上式中的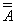 为增重
为增重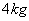 的金属丝的伸长量。
的金属丝的伸长量。
五、实验数据处理:
伸长量: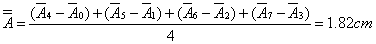
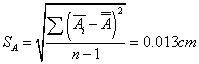
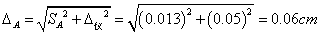
金属丝直径: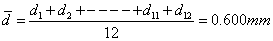
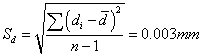

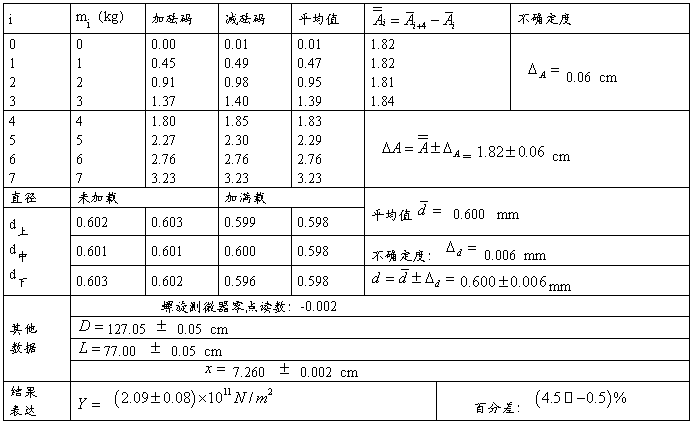
杨氏弹性模量:


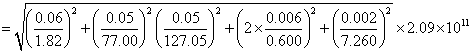
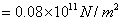
参考值:
百分差: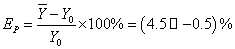
六、结果讨论及误差分析:
1、杨氏弹性模量的百分差在4.5%到—0.5%之间,该测量值在参考值区间内,误差一般。其误差产生的主要原因:根据杨氏弹性模量的误差传递公式可知,误差主要取决于金属丝的微小变化量和金属丝的直径,由于平台上的圆柱形卡头上下伸缩存在系统误差,用望远镜读取微小变化量时存在随机误差。
2、测量金属丝直径时,由于存在椭圆形,故测出的直径存在系统误差和随机误差。
3、实验测数据时,由于金属丝没有绝对静止,读数时存在随机误差。
4、米尺使用时常常没有拉直,存在一定的误差。
第二篇:用拉伸法测金属丝的杨氏模量参考报告
用拉伸法测金属丝的杨氏模量参考报告
一、实验目的
1.学会用拉伸法测量杨氏模量;
2.掌握光杠杆法测量微小伸长量的原理;
3.学会用逐差法处理实验数据;
4.学会不确定度的计算方法,结果的正确表达;
5.学会实验报告的正确书写。
二、实验仪器
YWC-1杨氏弹性模量测量仪(包括望远镜、测量架、光杠杆、标尺、砝码)、
钢卷尺(0-200cm ,0.1cm) 、游标卡尺(0-150mm,0.02mm)、螺旋测微器(0-25mm,0.01mm)
三、验原理
在外力作用下,固体所发生的形状变化称为形变。它可分为弹性形变和塑性形变两种。本实验中,只研究金属丝弹性形变,为此,应当控制外力的大小,以保证外力去掉后,物体能恢复原状。
最简单的形变是金属丝受到外力后的伸长和缩短。金属丝长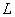 ,截面积为
,截面积为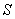 ,沿长度方向施力
,沿长度方向施力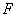 后,物体的伸长
后,物体的伸长 ,则在金属丝的弹性限度内,有:
,则在金属丝的弹性限度内,有:
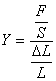
我们把Y称为杨氏弹性模量。
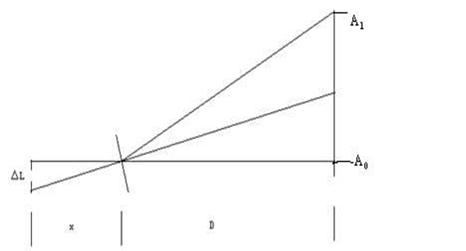
如上图:
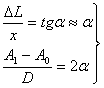

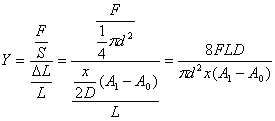
四、实验内容
<一> 仪器调整
1、杨氏弹性模量测定仪底座调节水平;
2、平面镜镜面放置与测定仪平面垂直;
3、将望远镜放置在平面镜正前方1.500-2.000m左右位置上;
4、粗调望远镜:将镜面中心、标尺零点、望远镜调节等高,望远镜的缺口、准星对准平面镜中心,并能在望远镜外看到尺子的像;
5、调节物镜焦距能看到尺子清晰的像,调节目镜焦距能清晰的看到叉丝;
6、调节叉丝在标尺0刻度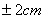 以内,并使得视差不超过半格。
以内,并使得视差不超过半格。
<二>测量
1、 下无挂物时标尺的读数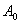 ;
;
2、依次挂上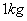 的砝码,七次,计下
的砝码,七次,计下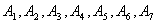 ;
;
3、依次取下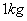 的砝码,七次,计下
的砝码,七次,计下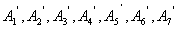 ;
;
4、用米尺测量出金属丝的长度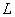 (两卡口之间的金属丝)、镜面到尺子的距离
(两卡口之间的金属丝)、镜面到尺子的距离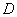 ;
;
5、用游标卡尺测量出光杠杆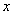 、用螺旋测微器测量出金属丝直径
、用螺旋测微器测量出金属丝直径 。
。
<三>数据处理方法——逐差法
1. 实验测量时,多次测量的算术平均值最接近于真值。但是简单的求一下平均还是不能达到最好的效果,我们多采用逐差法来处理这些数据。
2. 逐差法采用隔项逐差:

3. 注:上式中的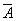 为增重
为增重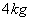 的金属丝的伸长量。
的金属丝的伸长量。
五、实验数据记录处理
(1)数据的记录
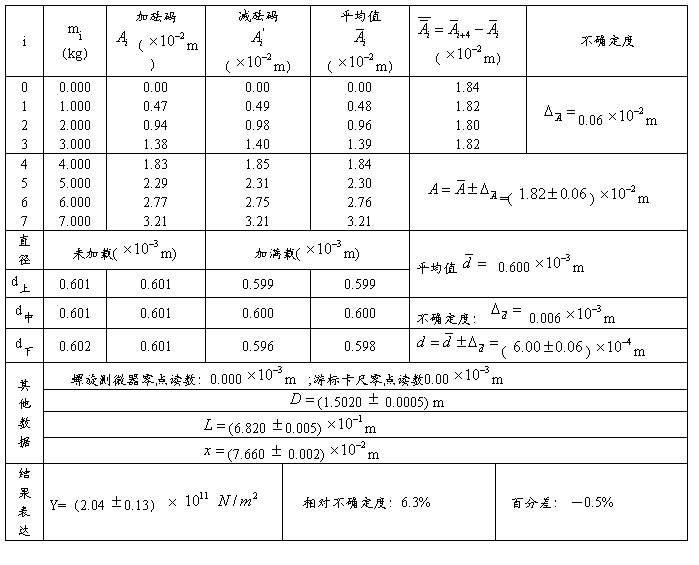
(2)数据处理
1、求
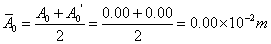 同理求得其它
同理求得其它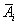 填入表中
填入表中
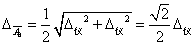 同理求得
同理求得
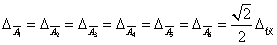
2、求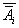
 同理求得
同理求得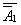 ,
, ,
,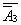 填入表中
填入表中
 同理求得
同理求得
3、求
金属丝伸长量
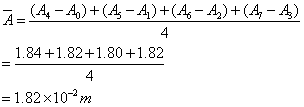


4、求金属丝直径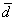

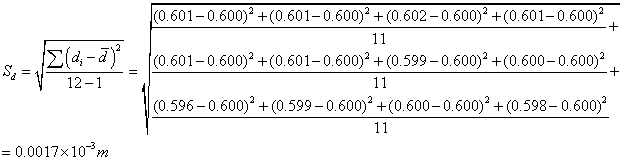

5、求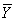
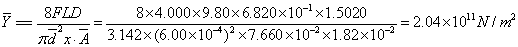
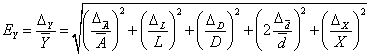
=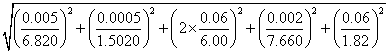
=6.3%
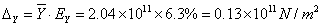
标准值: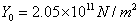
百分差:
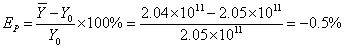
注:本实验百分差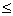 10%
10%
六、误差分析
1.误差主要取决于金属丝的微小变化量和金属丝的直径,由于平台上的圆柱形卡头上下伸缩存在系统误差,用望远镜 读取微小变化量时存在随机误差。
2.实验测数据时,由于砝码的摇晃使得金属丝没有绝对静止,读数时存在随机误差。
3.测量金属丝直径时,由于存在椭圆形,故测出的直径存在系统误差和随机误差。
4.测量D时米尺没有拉水平,测量L时米尺没有铅垂导致误差存在。
5.测量X时,由于作垂线没有完全的垂直,导致X值的测量存在误差。
本报告仅供参考格式。
数据、内容请勿抄袭!
-
用拉伸法测金属丝的杨氏弹性模量实验报告示范
实验报告示范1实验名称用拉伸法测金属丝的杨氏弹性模量一实验目的学习用拉伸法测定钢丝的杨氏模量掌握光杠杆法测量微小变化量的原理学习用…
-
大学物理实验-拉伸法测钢丝的杨氏模量(已批阅)
评分系学号姓名日期实验题目用拉伸法测钢丝的杨氏模量13393385实验目的采用拉伸法测定杨氏模量掌握利用光杠杆测定微小形变地方法在…
-
用拉伸法测金属丝的杨氏模量参考报告
用拉伸法测金属丝的杨氏模量参考报告一实验目的1学会用拉伸法测量杨氏模量2掌握光杠杆法测量微小伸长量的原理3学会用逐差法处理实验数据…
- 用拉伸法测金属丝的杨氏模量实验报告
-
大学物理实验 报告实验21 用拉伸法测杨氏模量
实验21用拉伸法测杨氏模量林一仙1实验目的1掌握拉伸法测定金属杨氏模量的方法2学习用光杠杆放大测量微小长度变化量的方法3学习用作图…
-
用拉伸法测金属丝的杨氏弹性模量实验报告示范
实验报告示范1实验名称用拉伸法测金属丝的杨氏弹性模量一实验目的学习用拉伸法测定钢丝的杨氏模量掌握光杠杆法测量微小变化量的原理学习用…
- 用拉伸法测金属丝的杨氏模量实验报告
-
用拉伸法测金属丝的杨氏模量参考报告
用拉伸法测金属丝的杨氏模量参考报告一实验目的1学会用拉伸法测量杨氏模量2掌握光杠杆法测量微小伸长量的原理3学会用逐差法处理实验数据…
-
大学物理实验 报告实验21 用拉伸法测杨氏模量
实验21用拉伸法测杨氏模量林一仙1实验目的1掌握拉伸法测定金属杨氏模量的方法2学习用光杠杆放大测量微小长度变化量的方法3学习用作图…
- 用拉伸法测金属丝的杨氏模量-实验报告
-
用拉伸法测金属丝的杨氏模量参考报告
用拉伸法测金属丝的杨氏模量参考报告一实验目的1学会用拉伸法测量杨氏模量2掌握光杠杆法测量微小伸长量的原理3学会用逐差法处理实验数据…