数学物理方法总结(改)
数学物理方法总结
第一章 复变函数
复数的代数式:z=x+iy
复数的三角式和指数式: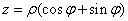 和
和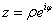
欧拉公式:{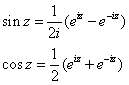
柯西-黎曼方程(或称为柯西-黎曼条件):{ (其中f(z)=u+iv)
(其中f(z)=u+iv)
函数f(z)=u+iv在点 及其领域上处处可导,则称f(z)在
及其领域上处处可导,则称f(z)在 点解析.在区域B上每一点都解析,则称f(z)是在区域B上的解析函数.
点解析.在区域B上每一点都解析,则称f(z)是在区域B上的解析函数.
解析函数的性质:1.若函数f(z)=u+iv在区域B上解析,则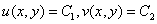 (
(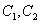 为常数)是B上的两组正交曲线族.
为常数)是B上的两组正交曲线族.
2.若函数在区域B上解析,则u,v均为B上的调和函数,即
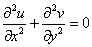
例题: 已知某解析函数f(z)的实部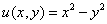 ,求虚部和这个解析函数.
,求虚部和这个解析函数.
解答: 由于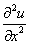 =2;
=2;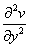 =-2;则
=-2;则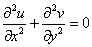
曲线积分法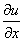 =2x;
=2x;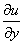 =-2y.根据C-R条件有:
=-2y.根据C-R条件有: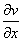 =2y;
=2y;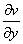 =2x.
=2x.
于是 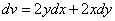 ;
;
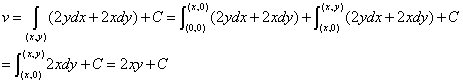 凑全微分显式法 由上式可知
凑全微分显式法 由上式可知 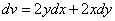
则易得 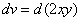
则显然 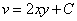
不定积分法上面已有 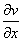 =2y;
=2y;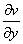 =2x
=2x
则第一式对y积分,x视为参数,有 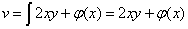 .
.
上式对x求导有 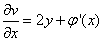 ,而由C-R条件可知
,而由C-R条件可知 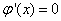 ,
,
从而 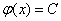 .故 v=2xy+C.
.故 v=2xy+C.
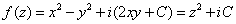
第二章 复变函数的积分
单连通区域柯西定理 如果函数f(z)在闭单连通区域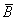 上解析,则沿
上解析,则沿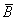 上任意一分段光滑闭合闭合曲线l(也可以是
上任意一分段光滑闭合闭合曲线l(也可以是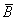 的边界),有
的边界),有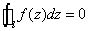 .
.
复连通区域柯西定理 如果f(z)是闭复连通区域上的单值解析函数,则
 .式中l为区域外边界线,诸
.式中l为区域外边界线,诸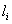 为区域内边界线,积分均沿边界线的正方向进行.即
为区域内边界线,积分均沿边界线的正方向进行.即
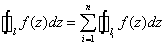 .
.
柯西公式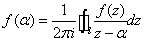
n次求导后的柯西公式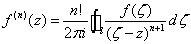
第三章 幂级数展开
幂级数
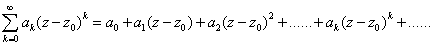
其中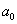 ,
,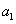 ,
,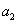 ,
,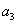 ,……都是复常数.
,……都是复常数.
比值判别法(达朗贝尔判别法)
1.若有

则 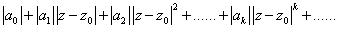 收敛,
收敛,
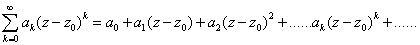 绝对收敛.
绝对收敛.
若极限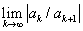 存在,则可引入记号R,
存在,则可引入记号R,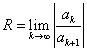 ,于是,若
,于是,若 ,则
,则
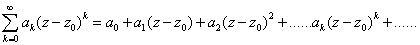 绝对收敛.
绝对收敛.
2.若 ,则后项与前项的模之比的极限
,则后项与前项的模之比的极限
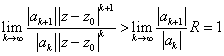 ,即说明
,即说明
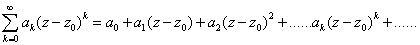 发散.
发散.
例题: 求幂级数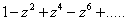 的收敛圆,z为复变数.
的收敛圆,z为复变数.
解答: 由题意可得
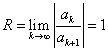
故 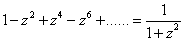 (
(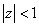 ).
).
泰勒级数展开设f(z)在以 为圆心的圆
为圆心的圆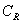 内解析,则对圆内的任意z点,f(z)可展为幂级数,
内解析,则对圆内的任意z点,f(z)可展为幂级数,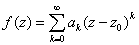 ,其中
,其中
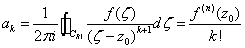 ,
,
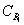 为圆
为圆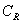 内包含z且与
内包含z且与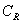 同心的圆.
同心的圆.
例题: 在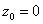 的领域上将
的领域上将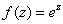 展开
展开
解答: 函数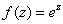 的各阶导数
的各阶导数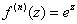 ,而
,而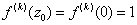 .
.
则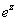 在
在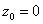 的领域上的泰勒展开
的领域上的泰勒展开
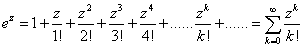 .
.
双边幂级数 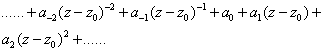
洛朗级数展开设f(z)在环形区域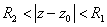 的内部单值解析,则对环域上的任一点z,f(z)可展为幂级数
的内部单值解析,则对环域上的任一点z,f(z)可展为幂级数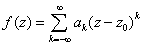 .其中
.其中
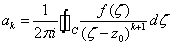 ,
,
积分路径C为位于环域内按逆时针方向绕内圆一周的任一闭合曲线.
例题1: 在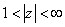 的环域上将
的环域上将 展为洛朗级数.
展为洛朗级数.
解答: 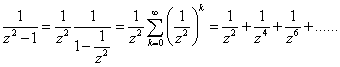
例题2: 在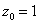 的领域上将
的领域上将 展为洛朗级数.
展为洛朗级数.
解答: 由题意得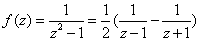
则有z-1的-1次项,而
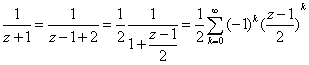 (
(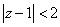 )
)
故  .
.
第四章 留数定理
留数定理设函数f(z)在回路l所围区域B上除有限个孤立奇点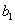 ,
, ,……,
,……,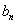 解析,在闭区域
解析,在闭区域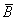 上除
上除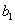 ,
, ,……,
,……, 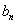 外连续,则
外连续,则
 .
.
其中,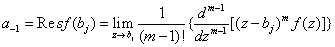 .
.
推论1: 单极点的留数为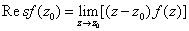 .
.
推论2: 若f(z)可以表示为P(z)/Q(z)的特殊形式,其中P(z)和Q(z)都在 点解析,
点解析, 是Q(z)的一阶零点(
是Q(z)的一阶零点( ).
). ,则
,则
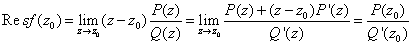 .
.
上式最后一步应用了罗毕达法则.
留数定理的应用
类型一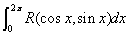 .作自变量代换
.作自变量代换  .则式子变为
.则式子变为
 .
.
例题: 计算 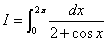 .
.
解答: 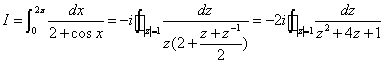 ,
,
Z的单极点为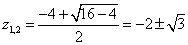 .
.
则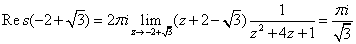 ,
,
由于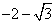 不在圆
不在圆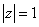 内.故
内.故 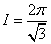 .
.
类型二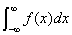 .积分区间是
.积分区间是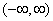 ;复变函数f(z)在实轴上没有奇点,在上半平面除了有限个奇点外是解析的;当z在上半平面及实轴上
;复变函数f(z)在实轴上没有奇点,在上半平面除了有限个奇点外是解析的;当z在上半平面及实轴上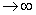 时,zf(z)一致地
时,zf(z)一致地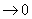 .则式子可以变为
.则式子可以变为
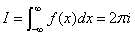 {f(z)在上半平面所有奇点的留数之和}.
{f(z)在上半平面所有奇点的留数之和}.
例题: 计算 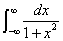 .
.
解答: 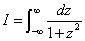 的单极点为
的单极点为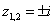 .
.
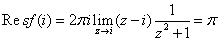 ,故
,故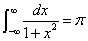 .
.
类型三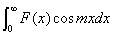 ,
,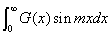 ,积分区间是
,积分区间是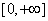 ;偶函数F(x)和奇函数G(x)在实轴上没有奇点,在上半平面除了有限个奇点外是解析的;当z在上半平面或实轴上
;偶函数F(x)和奇函数G(x)在实轴上没有奇点,在上半平面除了有限个奇点外是解析的;当z在上半平面或实轴上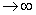 ,F(z)及G(z)一致地
,F(z)及G(z)一致地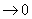 .则式子可以变为
.则式子可以变为
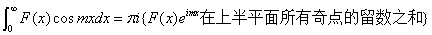 ;
;
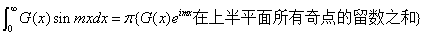 .
.
若类型二,类型三的实轴上有有限个奇点,则有
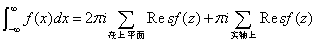 .
.
其中,在类型三中f(x)应理解为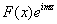 或
或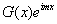 .
.
第五章 Fourier变换
傅里叶级数周期为2l的函数f(x)可以展开为级数
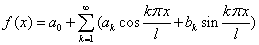 .
.
其中,{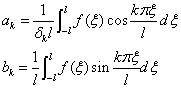 ,
, 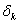 ={
={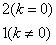 .
.
注: 积分上下限只要满足上-下=2l 即可.
复数形式的傅里叶级数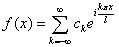
其中 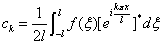 .
.
傅里叶积分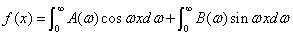
傅里叶变换式{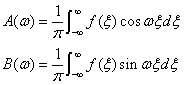
复数形式的傅里叶积分 {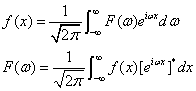
傅里叶变换的性质
(1) 导数定理 F[f’(x)]=iwF(w)
(2) 积分定理F[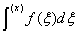 ]=
]=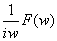
(3) 相似性定理F[f(ax)]=
(4) 延迟定理F[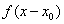 ]=
]=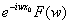
(5) 位移定理F[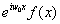 ]=
]=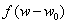
(6) 卷积定理若F[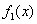 ]=
]=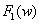 ,F[
,F[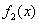 ]=
]=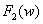 ,则
,则
F[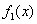 *
*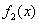 ]=
]=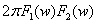 .
.
其中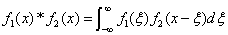 称为
称为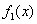 和
和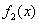 的卷积.
的卷积.
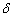 函数
函数
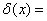 {
{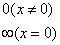 .
.
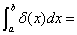 {
{ .
.
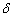 函数的一些性质
函数的一些性质
1. 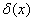 是偶函数.
是偶函数.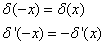
2. 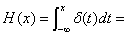 {
{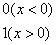 .
.
3.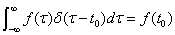 .
.
第六章 Laplace变换
拉普拉斯变换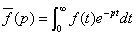
拉普拉斯变换的一些性质
(1) 线性定理若 ,
, ,则
,则
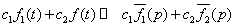 .
.
(2) 导数定理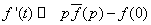 .
.
(3) 积分定理 L[
L[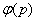 ].
].
(4) 相似性定理 .
.
(5) 位移定理 .
.
(6) 延迟定理 .
.
(7) 卷积定理若 ,
, ,则
,则
 ,
,
其中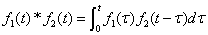 称为
称为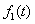 和
和 的卷积.
的卷积.
第七章 数学物理定解问题
(1) 均匀弦的微小振动,均匀杆的纵振动,传输线方程,均匀薄膜的微小横振动,流体力学与声学方程,电磁波方程的形式为 或
或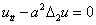 或
或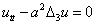 .
.
(2) 扩散方程,热传导方程的形式为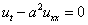 或
或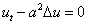 .
.
(3) 稳定浓度分布,稳定温度分布,静电场,稳定电流场方程的形式为(拉普拉斯方程)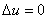 .
.
(4) 以上方程中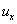 意为
意为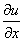 ,
,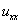 意为
意为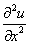 .若以上各方程均为有源,则方程为各方程=f(x,y,z,t).
.若以上各方程均为有源,则方程为各方程=f(x,y,z,t).
定解条件
初始条件初始”位移” 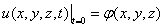 ,
,
初始”速度” 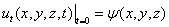 .
.
边界条件第一类边界条件 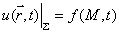
第二类边界条件 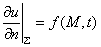
第三类边界条件 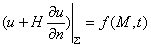
衔接条件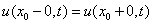
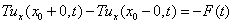 .(T为张力)
.(T为张力)
达朗贝尔公式定界问题
达朗贝尔公式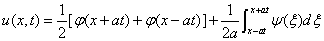 .
.
其中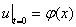 ,
,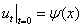 .
.
第八章 分离变数法
泛定方程 (若该方程可以使用分离变量法,则可以化成
(若该方程可以使用分离变量法,则可以化成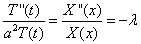 ).
).
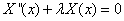 在不同的边界条件下解不同.
在不同的边界条件下解不同.
边界条件
(1) {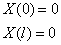 , X(x)的解为 {
, X(x)的解为 {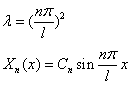 其中 n=1,2,3……
其中 n=1,2,3……
(2) {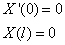 , X(x)的解为 {
, X(x)的解为 {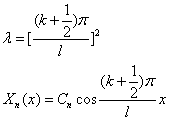 其中 k=0,1,2……
其中 k=0,1,2……
(3) {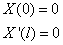 , X(x)的解为 {
, X(x)的解为 {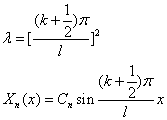 其中 k=0,1,2……
其中 k=0,1,2……
(4) {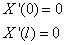 , X(x)的解为 {
, X(x)的解为 {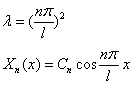 其中 n=0,1,2……
其中 n=0,1,2……
T(t)的方程在有n且n=0时的解为 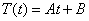 ;
;
在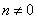 时的解为
时的解为
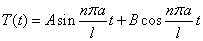 ;
;
在有k的情况下为
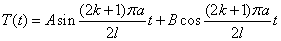 .
.
初始条件将u(x,t)=T(t)X(x)带入初始条件,确定u(x,t)中的常数项.
欧拉型常微分方程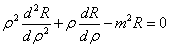 . 解法为做代换
. 解法为做代换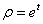 .
.
第九章 二阶常微分方程级数解法本征值问题
拉普拉斯方程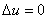
(1) 球坐标系下 .
.
分解为 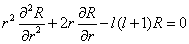 其解为
其解为 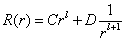 .
.
和 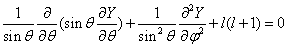 (球方程,
(球方程,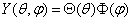 )
)
球方程又可以分离为 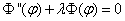 其中有
其中有 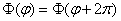 ,其方程解为 {
,其方程解为 {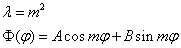 其中 m=0,1,2……
其中 m=0,1,2……
和 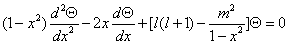 (连带勒让德方程).
(连带勒让德方程).
(2) 柱坐标系下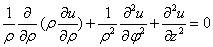 .分解为
.分解为
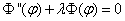 其中有
其中有 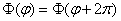 ,其方程解为
,其方程解为
{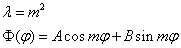 其中 m=0,1,2……
其中 m=0,1,2……
和 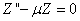 和
和 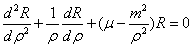 .
.
当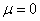 时,Z=C+Dz,
时,Z=C+Dz,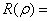 {
{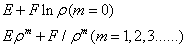 ;
;
当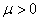 时,
时,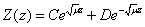 ,方程R转换为
,方程R转换为
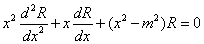 (
(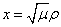 ,m阶贝塞尔方程).
,m阶贝塞尔方程).
当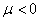 时,
时,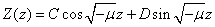 ,方程R转换为
,方程R转换为
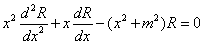 (
(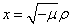 ,m阶虚宗量贝塞尔方程).
,m阶虚宗量贝塞尔方程).
亥姆霍兹方程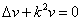 .
.
在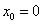 的领域上l阶勒让德方程的解为
的领域上l阶勒让德方程的解为 其中
其中
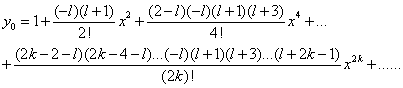
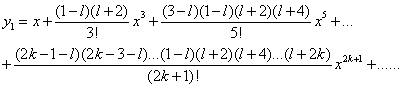
第十章 球函数
高次项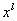 的系数
的系数 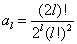 (在乘以适当的常数之后),用递推公式改写后为
(在乘以适当的常数之后),用递推公式改写后为
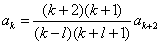 ,则
,则 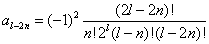 .则勒让德多项式为
.则勒让德多项式为 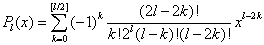 .
.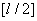 ={
={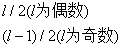 .
.
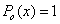

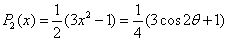
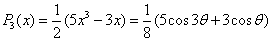
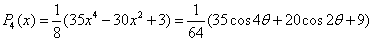 ……
……
勒让德多项式是正交的
例题1: 以勒让德多项式为基,在区间[-1,1]上把f(x)=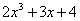 展开为广义傅里叶级数.
展开为广义傅里叶级数.
解答: 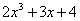 =
=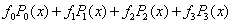
= 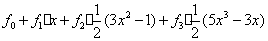
则有 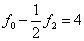 ,
, 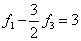 ,
, 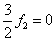 ,
, 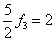 .
.
故有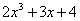 =
=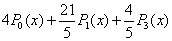 .
.
例题2: 在半径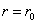 的球的内部求解拉普拉斯方程使满足边界条件
的球的内部求解拉普拉斯方程使满足边界条件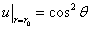 .
.
解答: 边界条件与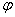 无关,故选择球坐标,则有
无关,故选择球坐标,则有
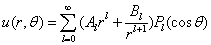 .
.
又有自然边界条件 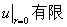 故
故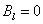 .则有
.则有
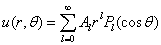 .
.
而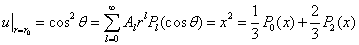 ,则
,则
 .
.
-
数学物理方法总结(改)
数学物理方法总结第一章复变函数复数的代数式zxiy复数的三角式和指数式zcossin和zei1izeeiz2i欧拉公式1izcos…
-
数学物理方法心得体会
数学物理方法心得体会电子信息学院李光圣96号数学物理方法是研究古典物理问题的数学方法其主要内容为将物理对象外化为函数物理规律外化为…
-
数学物理方法大总结
数学物理方法一填空题1函数为0ettx1dtx0又称为第二类欧拉积分的为zettz1dtRez002B函10数又称为第一类欧拉积分…
-
数学物理方法期末考试试题典型汇总
一Mathematicalmethodsforphysics二单项选择题每小题2分1齐次边界条件ux0tuxt0的本征函数是Asi…
-
数学物理方法
数学物理方法期末试题试卷说明1本试卷共6页考试时间110分钟2考试结束后将试卷与草纸一同交回院系专业班级答题栏请将答案填写到表格内…
-
数学物理方法大总结
数学物理方法一填空题1函数为0ettx1dtx0又称为第二类欧拉积分的为zettz1dtRez002B函10数又称为第一类欧拉积分…
-
数学物理方程小结
数学物理方程小结第七章数学物理定解问题数学物理定解问题包含两个部分数学物理方程即泛定方程和定解条件71数学物理方程的导出一般方法第…
-
数学物理方程读书报告
数学物理方程读书报告遥感与数字地球研究所徐焕20xx28007010031数学物理方程这门课主要是为非数学专业理工科研究生的公共选…
-
0 数学物理方程概述
数学物理方程概述什么是数学物理方程或数学物理方程是研究什么的关于方程含有未知数的等式叫做方程方程有多种多样例如函数方程含有未知函数…
-
数学物理方程期末考试试题及答案
一求解方程15分数学物理方程期末考试试题及答案utta2uxx0uxat0xuxat0x其中00解设xat则方程变为xatu0uF…
-
数学物理方法心得体会
数学物理方法心得体会电子信息学院李光圣96号数学物理方法是研究古典物理问题的数学方法其主要内容为将物理对象外化为函数物理规律外化为…