数学物理方法教学大纲

《数学物理方法》课程简介

课程编号：L2112113

英文名称：Methods of Mathematical Physics

学分：4

学时：64

授课对象：光电子技术科学专业

课程目标：

《数学物理方法》是物理类及光电子类本科专业学生必修的重要基础课，是在《高等数学》课程基础上的一门重要的应用数学类课程，为专业课程的深入学习提供所需的数学方法及工具。

课程内容：

复变函数（18学时），付氏变换（20学时），数理方程（26学时）

预修课程：

大学物理学、高等数学。

教材：

《数学物理方法》，科学出版社，邵惠民编著。

主要教学参考书：

《数学物理方法》，高教出版社，梁昆淼主编。

《数学物理方法》，高教出版社，郭敦仁主编。

《数学物理方法》，吴崇试主编

《数学物理方法》，中国科技大学出版社，严镇军编著。

《特殊函数概论》，北京大学出版社，王竹溪、郭敦仁编著。

《数学物理方法解题指导》，高等教育出版社，胡嗣柱、徐建军编。

"Mathematics of Classical and Quantum Physics" F.W. Byron & R.W. Fuller,

《数学物理方法》课程教学大纲

（Methods of Mathematical Physics）

一、基本信息

课程编号：L2112113

课程类别：学科基础课必修课

适用层次：本科

适用专业：光电子技术科学专业

开课学期：4

总学分：4

总学时：64学时

考核方式：考试

二、课程教育目标

《数学物理方法》是物理类及光电子类本科专业学生必修的重要基础课，是在《高等数学》课程基础上的一门重要的应用数学类课程，为专业课程的深入学习提供所需的数学数学方法和工具。因此本课程应受到相关专业学生和教师的重视。
　　对实际的工程、技术、科学问题，通常需要转换为物理问题，然后利用物理原理进一步翻译为数学问题，进一步求解该数学问题，再将得到的数学结果翻译成物理问题，即讨论所得结果的物理意义。因此，数学是物理的语言之一，《数学物理方法》是联系数学和物理类及光电子类专业课程的纽带。本课程的主要任务就是告诉学生如何将各种物理问题翻译成数学的定解问题，并了解、掌握求定解问题的若干方法，如行波法、分离变数法、付里叶级数法、幂级数解法、积分变换法、保角变换法、格林函数法、电像法等。

三、教学内容与要求

教学内容：

1复变函数部分

复变函数基本知识、复变函数积分、复变幂级数、留数定理及应用、拉普拉斯变换简介。

2付氏变换部分

付里叶级数、付里叶级数应用、付里叶积分、付里叶积分应用、

3数理方程部分

数理方程的建立、数理方程的定解条件、二阶线性偏微分方程的分类、数理方程的求解（行波法、分离变数法、其它方法）、二阶常微分方程的级数解法、特殊函数（球函数、柱函数）。

基本要求：

1作为光电子专业的专业基础课，本课程强调数学在物理学中的应用。

2本课程强调对所学内容在宏观上的了解，和部分重点内容的掌握。

3本课程包含了复变函数、付氏变换、数理方程三个相对独立部分。其中复变函数是基础，要求了解基本思想和掌握适量的常用计算。付氏变换是本专业学生进行专业学习和工作所必备的工具，因此对基本思想要求理解，常用计算要求熟练掌握。数理方程部分是本课程的核心，但由于学科特点和学时所限，强调对基本思想和重要结论的了解及掌握简单的计算。

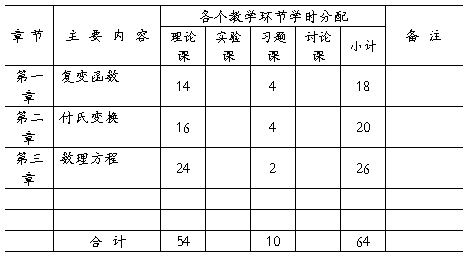
四. 各个章节学时分配

第一章复变函数18学时

1-1复变函数基本知识2学时

1-2复变函数积分4学时

1-3复变幂级数4学时

1-4留数定理及应用2学时

1-5拉普拉斯变换简介2学时

习题4学时

第二章付氏变换20学时

2-1付里叶级数4学时

2-2付里叶级数应用4学时

2-3付里叶积分4学时

2-4付里叶积分应用4学时

习题4学时

第三章数理方程26学时

3-1数理方程的建立4学时

3-2数理方程的定解条件2学时

3-3二阶线性偏微分方程的分类2学时

3-4数理方程的求解（行波法、分离变数法、其它方法）8学时

3-5二阶常微分方程的级数解法4学时

3-6特殊函数（球函数、柱函数）4学时

习题2学时

学时分配表

五. 预修课程

大学物理学、高等数学。

六.成绩评定

成绩评定方式：考试

成绩结构比例：期末成绩70%+平时成绩30%

编写人（签字）：赫然编写人职称：教授

审阅人（签字）：审阅人职称：

审批人（签字）：审批人职务：

本大纲启用日期： 20## 年5 月 10日

第二篇：数学物理方法答案-部分

数学物理方法习题解答

向安平

Bxiangap@sina.comxiangap@163.com成都信息工程学院光电技术系20xx年4月30日

前言

本书供电子科学与技术专业和光信息科学与技术专业《数学物理方法》课程教学使用．本教学参考书仅供授权读者在计算机上阅读，不能编辑、拷贝和打印．经作者授权，可取消全部限制．

在第一版中只收录了必要的试题，以后将增补习题的数量和类型，在每章增加内容小结和解题方法讨论．欢迎读者提供建议．

作为本书的第一版，错误和排版差错在所难免，敬请读者指正．

向安平

20xx年9月30日

目录iii

............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

DepartmentofOptoelectronics

ChengduUniversityofInformationTechnology

1225558xxxxxxxxxxxx1121214151517232xxxxxxxxxxxx3335

Bxiangap@sina.comT85966382c2003–XiangAnping?

AllRightsReserved

iv目录

3637373839394242464646

....................................................................47.................................................................48

Bxiangap@sina.comT85966382DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?

AllRightsReserved

第一篇复变函数概论

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第一章复变函数

§1.1复数与复数运算

1.下列式子在复平面上各具有怎样的意义?

(1)|x|≤2.

(2)|z?a|=|z?b|（a、b为复常数）.

(3)Rez>1

(1)|x|≤2

解一：|z|=|x+iy|=部．?≤2，或x2+y2≤4．这是以原点为圆心而半径为2的圆及其内

解二：按照模的几何意义，|z|是复数z=x+iy与原点间的距离，若此距离总是≤2，即表示以原点为圆心而半径为2的圆内部．

(2)|z?a|=|z?b|(a、b为复常数)．

解一：设z=x+iy,z=a1+ia2,b=b1+ib2；

?|z?a|=(x?a1)+(y?a2),?|z?b|=(x?b1)+(y?b2),

于是

(x?a1)2+(y?a2)2=(x?b1)2+(y?b2)2,

即

(2y?a2?b2)(b2?a2)=(2x?a1?b1)(a1?b1)

by?a+a1?b1=.b?ax?22ba+b这是一条直线，是一条过点a和点b连线的中点(a+

,)且与该直线垂直的直线．

解二：等式的几何意义是，点z到定点a和点b的距离相等的各点的轨迹，即表示点a和点b的连线的垂直平分线．

(3)Rez>1

．

11解：设z=x+iy，则Rez=x，故原式为x>1

，它表示x>的半平面，即直线x=右边的

区域（不包括该直线）．

2.把下列复数用代数式、三角式和指数式几种形式表示出来．

(1)i.

(2)?1.√(3)1+i.

(4)(1?i)/(1+i).

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第一章复变函数(1)i．

解：i本身即为代数式，此时在z=x+iy中，x=0、y=i；三角式：

ρ=?

?x2+y2=

?=arctany??1,?

所以x=arctan10=π2,

z=i=cos(ππ

指数式：2)+isin(2);

z=i=eiπ.

(1)?i．

解：?i本身即为代数式．

三角式：

z=cos(π)+isin(π).

指数式：

z=eiπ.

(3)1+i√.

解：z=1+i√本身即为代数式．

三角式为：

ρ=i2+√(3)2=2,

?=arctgπ

?1=,

π3π?

z=2cos3+isin3.

指数式为:

z=2eiπ.

(4)1?i

．

解：代数式：

z=1?i

三角式：因ρ=1,?=arctan=31+i=12(1?i)2=?i.

π，所以

z=cos3π3π

指数式：2+isin2.

z=ei3π.

3.计算下列数值（a、b和?为实常数）．

(1)√.

Bxiangap@sina.comDepartmentofOptoelectronicsT85966382ChengduUniversityofInformationTechnology3?c2003–XiangAnpingAllRightsReserved

4§1.1复数与复数运算

(2)√3i.

(3)cos5?.

√(1)．

解：先化a+ib为三角式

√a+ib=a2+b2(cos?+isin?),

abcos?=,sin?=.2222a+ba+b

??√√4??a+ib=a2+b2cos+isin22????√411=a2+b2(1+cos?)+i(1?cos?)22

????√41a1a=a2+b21++i1?22a+ba+b√????=a2+b2+a+ia2+b2?a.2于是，(2)√3?解：因

所以i=1cos?π?2+2nπ+isin?π

2??+2nπ,

??????√√π2π233i=1cos+nπ+isin+nπ,6363√π23i=ei(+nπ).

(3)cos5?．

解：由乘幂的公式

(cos?+isin?)n=cosn?+isinn?).

及二项式定理

(a+b)n=an+nan?1b+

可知

cos5?+isin5?=(cos?+isin?)5

=cos5?+i5cos4?sin??10cos3?sin2??i10cos2?sin3?+5cos?sin4?+isin5?.

比较等式两边的实部和虚部得

cos5?=cos5??10cos3?sin2?+5cos?sin4?,

sin5?=5cos4?sin??10cos2?sin3?+sin5?.n!n(n?1)n?22ab+···+an?kbk+···.2!(n?k)!k!

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第一章复变函数5

§1.2复变函数

1.计算下列数值（a和b为实常数，x为实变数）．

(1)sin(a+ib).

(2)cosix.

(3)sinix.

(1)sin(a+ib)．

解：

sin(a+ib)=1i(a+ib)[e?e?i(a+ib)]2i

1=[e?b(cosa+isina)?eb(cosa?isina)]2i

1=[e?bsina+ebsina+i(ebcosa?e?bcosa)]2

1=[(eb+e?b)sina+i(eb?e?b)cosa].2

(2)cosix．

解：

ei(ix)?e?i(ix)ex+e?x

==chx.cosix=22

(3)sinix．

解：

ei(ix)?e?i(ix)ex?e?x

sinix==i.2i2

§1.3

无作业导数

§1.4解析函数

1.某个区域上的解析函数如为实函数，试证它必为实常数．

2.已知解析函数f(z)的实部u(x,y)或虚部v(x,y)，求该解析函数．

(1)u=exsiny.

(2)u=x2?y2+xy,f(0)=0.

(3)u=lnρ,f(1)=0.

3.试从极坐标系中的柯西—黎曼方程（1.3.4）消取u或v．本题答案就是Laplace方程（1.4.2）在极坐标系中的表示式．

1.某个区域上的解析函数如为实函数，试证它必为实常数．

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

6§1.4解析函数

解：设这个解析函数为w(z)=u(x,y)+iv(x,y)，因为它是实数，所以v(x,y)≡0；因为它是解析函数，所以满足C—R条件

?u?v=,?x?y

注意到v(x,y)≡0，则

?u=0?x

?u=0?y(1-1)(1-2)?v?u=.?x?y

由式(1)知，u=f1(y)，由式(2)知u=f2(x)；因为x、y在该区域中皆为独立变数，要f1(x)=f2(x)，则只有f1(x)=f2(x)=常数，即u必为常数，亦即必为常数．该解析函数

2.已知解析函数f(z)的实部u(x,y)或虚部v(x,y)，求该解析函数．

(1)u=exsiny．

解一：

?u=exsiny,?x

根据C—R条件，则

?v=exsiny,?y

于是

dv=?v?vdx+dy=?excosydx+exsinydy?x?y

=d(?excosy).?v=?excosy.?x??u=?excosy.?y

所以

v(x,y)=?excosy+C.

f(z)=exsiny+i(?excosy+C)

=?iex(cosy+isiny)+iC

=?iex·eiy+iC

=?iex+iy+iC

=?iez+iC.

解二：因为

?v=?excosy,?x

?v=exsiny.?y

所以，由式(1)，暂且可把y当作参数，对x积分，

?(1-3)(1-4)

v(x,y)=?excosydy+?(y)=?excosy+?(y).(1-5)

c2003–XiangAnping?

AllRightsReservedBxiangap@sina.comT85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnology

第一章复变函数7式(3)对y求偏导数，

?v=exsiny+??(y)?y

比较式(2)和式(4)得??(y)=0，即?(y)=C．所以

v(x,y)=?excosy+C,

f(z)=exsiny+i(?excosy+C)=?iez+iC.

必须指出：下面各题都可用这两种方法求解，限于篇幅，我们将只给出任一种．(1-6)

(2)u=x2?y2+xy,f(0)=0.

解：因

??u?v

=2x+y=,

??u2y?x=?v

则

dv=(2x+y)dy+(2y?x)dx

=d(2xy+1y21

2)+d(2xy?2x2)

=d(2xy+1y2?1x2

22),

v=2xy+1

2(y2?x2)+C.

所以

f(z)=x2?y2+xy+i2xy+1?

(y2?x2)+iC

?2?

=x2?y2+i2xy?1

2i(x2?y2)?xy+iC

=(x+iy)2?i1?

2(x2?y2)+i2xy?+iC

=z2?i1

2z2+iC.

又因f(0)=0+iC=0，则C=0，从而

f(z)=z21?i?

(3)u=lnρ,f(1)=0.

解：因为??u1?v1

==,

1?u?v

=?=0.

则

dv=d?

v=?+c.

所以

f(z)=lnρ+i?+ic=ln|z|+iargz+ic=lnz+ic.

Bxiangap@sina.comDepartmentofOptoelectronics

T85966382ChengduUniversityofInformationTechnology?c2003–XiangAnpingAllRightsReserved

8§1.5平面标量场因f(1)=0+ic=0．则c=0，从而

f(z)=lnz.

3.试从极坐标系中的柯西—黎曼方程（1.3.4）消取u或v．本题答案就是Laplace方程（1.4.2）在极坐标系中的表示式．

解：C—R防程可改写为

?u?vρ=,

1?u?v?=.

上式第1式两边对ρ微分一次，二式两边对?微分一次，

????u?2v?ρ=,?

上式第一式减第二式，得?1?u?=2?2v.?u?ρ?ρ?ρ

这就是极坐标系下的Laplace方程之一．

C—R条件还可以改写为

??1?2u+=0ρ???u

1?v=,v=?ρ?.

上式第一式对?微分一次，第二式对ρ微分一次，并相减得极坐标系下的另一Laplace方程，????v1?2vρ+=0?ρ?ρρ??2

§1.5

无作业．平面标量场

§1.6

无作业．多值函数

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第二章复变函数的积分9

第二章复变函数的积分

§2.1

无作业．

复变函数的积分

§2.2

无作业．

柯西定理

§2.3

无作业．

不定积分

§2.4

柯西公式

1.已知函数Ψ(t,x)=e2tx?t．把x作为参数，把t认为是复变数，试应用柯西公式把?|t=0表为回路积分．

对回路积分进行积分变数的代换～t=x?z，并借以证明

?nΨnx2d?x2

.=(?1)ee

?tndxn

(本题的Ψ(t,x)是埃尔米特多项式的母函数，见附录九)．Ψ

解：(i)把?表为回路积分如下：

?nΨn!

|=t=0?tn2πi

=2πi

(ii)证明：以ξ=x?z代入上式

?nΨn!

|=t=0?tn2πi

=2πi

?逆

e2ξx?ξ

dξ

(ξ?t)n+1e2ξx?ξ

dξ.ξn+1

?逆

ex?z(x?z)n+1

d(?z)

ex·e?z

(?1)n(z?x)n+1dzx??

(?1)ne?z2dz2n!x

2πi?(z?x)n

nx2d?x2

=(?1)ee,得证.

dxn

Bxiangap@sina.comT85966382DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?

AllRightsReserved

第三章幂级数展开

§3.1

无作业．复数项级数

§3.2幂级数

1.把幂级数(3.2.1)逐项求导，求所得级数的收敛半径，以此验证逐项求导并不改变收敛半径．

2.把幂级数(3.2.1)逐项积分，求所得级数的收敛半径，以此验证逐项积分并不改变收敛半径．

3.求下列幂级数的收敛圆．

?∞1k(1)k=1(z?i),

?∞?z?k(2),k=1?∞kk(3)k=1k(z?3).

1.把幂级数(3.2.1)逐项求导，求所得级数的收敛半径，以此验证逐项求导并不改变收敛半径．

解：该幂级数的收敛半径是：

???ak??.R=lim?

k→∞?ak+1?对该幂级数逐项求导得：∞d?ak(z?z0)k=a1+2a2(z?z1)+···+kak(z?z0)k?1+(k+1)ak+1(z?z0)k+···.dzk=0其收敛半径为

????kak??R=lim?t→∞(k+1)ak+1?????ak??=lim??t→∞?1+ak+1????ak??.=lim?

t→∞?ak+1?

所以逐项求导并不改变其收敛半径．

2.把幂级数(3.2.1)逐项积分，求所得级数的收敛半径，以此验证逐项积分并不改变收敛半径．

解：对幂级数逐项积分，得：

??∞11ak(z?z0)kd(z?z0)=a0(z?z0)+a1(z?z0)2+a2(z?z0)3+···+23k=0

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第三章幂级数展开11

=+用同上题的方法可得收敛半径为11ak(z?z0)k+1+ak+1(z?z0)k+2+···.k+1k+2???ak??.R=lim??t→∞ak+1?

所以逐项积分并不改变收敛半径．

3.求下列幂级数的收敛圆．?∞1(1)k=1(z?i)k.

解：其收敛半径为?????k+1??1/k??=lim??R=lim????k→∞k→∞1/k+1k?

????1?=11+=lim??k→∞k?

所以收敛圆为|z?i|=1．?∞?z?k(2)k=1.

解：收怜半径为

????k+1????k?k?=lim?(k=1)?R=lim??k→∞?(k+1)?(k=1)?k→∞?kk

???1?k=1??k?=lim?k++(k=1)k+···??kk→∞k

=lim|k+(k+1)+···|=∞,k→∞

1R=lim=lim=∞.k→∞kk→∞1k

所以只要z是有限的，此幂级数就是收敛的，收敛圆为|z|=R<∞．?∞k(3)k=1k(z?3)k.

解一：收敛半径为

111=limR=lim=lim=0.kk→∞kk→∞kkk→∞k

解二：收敛半径为

??k????k?1????R=lim?=lim[k+(k+1)+···]=0.k→∞(k=1)k+1?k→∞

所以收敛圆为|z?3|=0，只要z?3，此幂级数就发散．

§3.3泰勒级数展开

1.在指定的点z0的邻域上把下列函数展开为泰勒级数．(1)√m在z0=1.

(2)e1/(1?z)在z0=0.(1)√m在z0=1.

DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReservedBxiangap@sina.comT85966382

12§3.4解析延拓

解一：因为

f(z)=z11f?(z)=z?1

1?m?2

f??(z)=1z

?2m)1

f???(z)=(1?m)(1e?3......

故其泰勒展式为

f(z)=1+

解二：注意到解一：因为

f(z)=e1

f?(z)=e(1?z)?2

?1????2?2?3f(z)=e(1?z)·(1?z)+2(1?z)

?1?

f???(z)=e(1?z)?6+2(1?z)?5+4(1?z)?5+6(1?z)?4......

故其泰勒级数为

313

f(z)=e1+z+z2+z3+······

2!3!

解二：注意到几何级数

?1=zk

1?zk→0

∞

,,,,,f(1)的主值=1;

f?(1)=;

f??(1)=1;

?2m)

f???(1)=(1?m)(1;......

11?m(1?m)(1?2m)2(z?1)+(z?1)+(z?1)3+······23m2!m3!m

√m

=[1+(z?1)]1/m，则根据二项式定理也可求出上述答案．

(2)e1/(1?z)在z0=0.

,,,,,f(0)=e;f?(0)=e;f??(0)=3e;f???(0)=13e;......

(|z|<1).

则

e=e1+=e·e????2

z1z

=e1+++······

1?z2!1?z??

=e1+(z+z2+z3+······)+(z+z2+z3+······)2+······

????

1211

=e1+z+(1+)z+1++z3+······

22!3!

32133

(|z|<1).=e1+z+z+z+······

2!3!

§3.4

无作业．

解析延拓

§3.5洛朗级数展开

在挖去奇点z0的环域上或指定的环域上把下列函数展开为洛朗级数．

Bxiangap@sina.com

T85966382DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?

AllRightsReserved

第三章幂级数展开13

(1)z5e1/z在z0=0.

(2)1/(z?2)(z?3)在|z|>3.(3)1/(z2?3z+2)在1<|z|<2.(1)z5e1/z在z0=0.解：由

et=1+t+

知

e1/z=1+

所以

112

t+···+tn+···,2!n!

(|t|<∞)

11111++···++···,z2!z2n!zn

11312

z+z+···+z5?n+···,2!3!n!

(0<|z|),

f(z)=z5e1/z=z5+z4+

(2)1/(z?2)(z?3)在|z|>3.解：因为

(0<|z|).

1(z?2?(z?3)11==?

(z?2)(z?3)(z?2)(z?3)z?3z?2

1111

=?,z1?z1?并注意到当|z|>3时，有

z1?

以及

?1∞??3k

==3?(k+1)zk,k+1zk=0k=?∞

11z1?

所以

?1??∞

2?(k+1)zk,

?1???1

3?(k+1)?2?(k+1)zk=

(z?2)(z?3)k=?∞

(|z|>3).

(3)1/(z2?3z+2)在1<|z|<2.解：原式可改写为

1111

==?,

z2?3z+2(z?1)(z?2)z?2z?1

=?z?21?

而

z?z?2?z?31

=?1+++···,

2222

??z??

??<1,|z|<2,2

=?z?11?

???2??3

1111=?1++++···

zzzz

c2003–XiangAnping?

AllRightsReserved

Bxiangap@sina.comT85966382DepartmentofOptoelectronics

ChengduUniversityofInformationTechnology

?§3.6孤立奇点的分类

所以1111+2+3+4+···,zzzz??????1???<1,|z|>1.?z?

∞?111??z?k?k=??zz2?3z+22k=02k=?∞∞?1??zkkz,=??k+1(1<|z|<2).

无作业．

Bxiangap@sina.comT85966382k=02k=?∞§3.6孤立奇点的分类DepartmentofOptoelectronicsChengduUniversityofInformationTechnology?c2003–XiangAnpingAllRightsReserved

第四章留数定理15

第四章留数定理

§4.1留数定理

1.确定下列函数的奇点，求出函数在各奇点的留数．

(1)ez/(1+z).

(2)z/(z?1)(z?2)2.

(3)1/(z3?z5).

(4)z2/(z2+1)2.

(5)1/(1+z2n).

2.计算下列回路积分．

?dz22(1)?(?的方程是x+y?2x?2y=0).?z(2)|z|=1cosdz.

?f(z)13.应用留数定理计算回路积分?dz，函数f(z)在?所围区域上是解析的，α是该区域

的一个内点．

(1)ez/(1+z).

解：(i)因为

z→?1?limez1+z?=∞,

所以z0=?1是函数的极点．又因??z??e1lim(1+z)=limez=,z→?1z→?11+ze

这是非零有限值，所以z0=?1是函数的一阶极点（或称单极点），其留数就是1/e，即

1Resf(?1)=.e

?ez

lim不存在,z→∞1+z

所以z0=∞是函数的本性奇点．函数在全平面上只有这两个奇点，由于全平面上所有奇点的留数之和为零，所以

1Resf(∞)=?{f(z)在所有（有限个）有限远奇点的留数之和}=?Resf(?1)=?.e(ii)因为?

以下各题皆应如此分析，但限于篇幅，我们只给出简捷的步骤．

(2)z/(z?1)(z?2)2.

解：(i)单极点z0=1．

(ii)又二阶极点z0=2，

dResf(2)=limz→2dzResf(1)=lim?z=1.z→1(z?2)2zz?1?

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

=lim?=?1.z→2z?1(z?2)2

§4.1留数定理

(3)1/(z3?z5).解：

f(z)=

(i)单极点z0=1,

z3?z5z3(1?z2)

?11

=?.

z3(z+1)2?

=?.

z3(1?z)2

Resf(1)=lim?

z→1

(ii)单极点z0=?1,

Resf(?1)=lim

(iii)　三极极点z0=0,

z→?1

??1d21

Resf(0)=lim

z→02!dz1?z??128z2

=lim+=1z→02!(1?z2)2(1?z2)2

或

Resf(0)=?[Resf(1)+Resf(?1)]=1.

(4)z2/(z2+1)2.

解：(i)二阶极点z0=i，

dz2i

Resf(i)=lim=?.

z→idz(z2+1)24

(ii)二阶极点z0=?i，

iResf(?i)=?Resf(i)=.

(5)1/(1+z2n).

解：令原式分母1+z2n=0,z2n=?1，

zn=±i=e

所以

z0=e

为实函数f(z)的单极点，

z?ei(2k+1)π/2n

Resf(z0)=lim,

z→z01+z2n

应用罗毕达法则，则

Resf(z0)=lim

11?i(2n?1)(2k+1)π

z→z02nz2n?12n

11ei(2k+1)π/2n

·i(2k+1)π=?ei(2k+1)π/2n.=

2ne2n

i(2k+1)πi(2k+1)π

(k=0,1,2,···,2n?1)

2.计算下列回路积分．?dz22(1)?(?的方程是x+y?2x?2y=0).

√2

解：?的方程可化为：(x?1)+(y?1)=(2)，在复平面上，它是一个以(1,i)为圆√

心，Bxiangap@sina.comT85966382DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?

AllRightsReserved

第四章留数定理17

被积函数f(z)=1/(z2+1)(z?1)2，它有两个单极点z0=±i，和一个二阶极点z0=1，在这三个极点中，z0=?i不在积分回路内，只有极点z0=i和z0=1在积分回路内，它们的留数分别为：

11=,Resf(i)=limz→i(z+i)(1?z)24

d1?2z1Resf(1)=lim=lim=?.z→1dz1+z2z→1(1+z2)22

应用留数定理：???dz11πi=2πi[Resf(i)+Resf(1)]=2πi?=?.2+1)(z?1)2(z422??z(2)|z|=1cosdz.

解：被积函数f(z)=cosz/z3的三阶极点z0=0在单为圆内，其留数为

1d21Resf(0)=lim2(cosz)=?,2!z→0dz2

所以

coszdz=2πiResf(0)=?πi.3z|z|=1?f(z)13.应用留数定理计算回路积分?dz，函数f(z)在?所围区域上是解析的，α是该区

域的一个内点．

(z)解：设被积函数g(z)=f．因为f(z)在?所围区域内是解析的，所以g(z)在积分回路（即

?所围区域）内只有一个单极点z0=α，而??f(z)(z?α)=f(α),Resf(α)=limz→αz?α

所以?f(z)zdz=2πiResf(α)=2πif(α),

?z?α于是?1f(z)dz=f(α).2πi?z?α

这正是柯西公式．?

§4.2应用留数定理计算实变函数定积分

1.计算下列实变函数定积分．

?2πx(1)0d.?2πx(2)0d(0<ε<1).?2πcos22xdx(3)0(|ε|<1).?πadx(4)0a2+sinx(a>0).

?π/2dx(5)0.

2.计算下列实变函数定积分．

?∞2+1(1)?∞x

dx.?∞x2dx(2)0.

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

18§4.2应用留数定理计算实变函数定积分

3.计算下列实变函数定积分．

?∞x(1)?∞x

sindx.?∞cosmx(2)0dx.?∞eimx?∞imx(3)?∞edx,?∞dx,

1.计算下列实变函数定积分．

(1)?2π

0dx

.(m>0,Reα>0).

解：这是属于类型一的积分，为此，做变换z=eix使原积分化为单位圆内的回路积分??dz/iz2dz=I=z+z|z|=1iz+4z+1|z|=12+?dz2=i|z|=1(z+2?z+2+?2f(z)dz.=i|z|=1√√f(z)有两个单极点z0=?2±，其中z0=?2+在单位圆内，且??√11Resf(3?2)=lim=.2z→2z+2+

I=2πi·√22πResf(3?2)=.i和本题一样，下面的几个小题都属于类型一的积分，处理方法和本题类似，因此，我们将只给出简捷的步骤．

(2)?2π

0dx

(0<ε<1).

解：作变换z=eix，则

I=?

|z|=1

4=2iε=4

iε2??dz/izε?11+(z+z)zdzz2+2z|z|=1+1f(z)dz.|z|=1√√2)，其中z=1(?1+f(z)有两个二阶极点z0=11?ε1?ε2)在单位圆内，且(?1±0??√1ε22Resf(?1+1?ε)=.ε4(1?ε2)3/2??√41I=2πi·2Resf(?1+1?ε2)iεε

2π=.(1?ε2)3/2

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第四章留数定理19

(3)?2π

0cos22xdx

(|ε|<1).

,解：令z=eix，则dx=

?cosx=?4?21+z21+z2,dzcos2x=1+z4，以此代入原式得I=|z|=1z21?2ε1+

+ε

|z|=1?1(1+z4)2dz=4i|z|=1z(1?ε)(z?ε)?1=f(z)dz.4i|z|=1(1+z4)2dz4iz4[?εz2+(1+ε2)z?ε]

被积函数的极点是：四阶极点z0=0，单极点z0=ε，1

，因|ε|<1，则|1/ε|>0，故只有

z0=0和z0=ε两个极点在单位圆内，其留数分别为：

??1d3(1+z4)2

Resf(0)=lim3!z→0dz3(1?εz)(z?ε)??d2(1+z4)2[2εz?(1+ε2)]8z3(1+z4)1lim+=3!z→0dz[(1?εz)(z?ε)](1?εz)(z?ε)

..=.

(1+ε2)(1+ε4)=?,ε4

?(1+ε4)2(1+z4)2

=4.Resf(ε)=lim4z→εz(1?εz)ε(1?ε2)?

??1(1+ε4)2(1+ε2)(1+ε4)I=2πi·?4iε(1?ε)ε(1+ε4)π=.1?ε2

?π(4)adx0a+sinx(a>0).

解：把原式化为??1πadxady1π

I=+20a2+sinx20a2+siny

在后一个积分中，令y=x?π，则上式可表为

???1πadx12πadxa2πadxI=+=20a2+sinx2πa2+sinx20a2+sinx?adz=2|z|=1iz[a+(z+z)/(2i)]?adz=?1?1z+zz?z2|z|=1iza+a?Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

20§4.2应用留数定理计算实变函数定积分

?2azdz=?

i|z|=1(z2+2az?1)(z2?2az?1)

zdz2a

==?

i|z|=1(z+a+a+1)(z+a?a+1)(z?a+a+1)(z?a?a+1)?2a=?f(z)dz.

i|z|=1

√√f(z)在单位圆内有单极点z0=?a+a+1及z0=a?a+1，且

√

√?a+Resf(?a+a2+1)=2a+1·2·(?a+a+1)(?2a)?1=,28aa+1

√

√a?a+12Resf(a?a+1)=

2a·2(a?a+1)·2(?a+1)

?1.=

8a?π

adx2a1π

=2πi=.2+sinxia?4aa+1a+10

?π/2

(1)

解：因被积函数是偶函数，故可作延拓

1I=

02π

dx1

1+cos2x4

|z|=1

dzz2+11+

zdz1

i|z|=1z4+6z2+1?1zdz

i|z|=1[z2+3+22][z2+3?22]?1zdz

,=i|z|=1[z2+(3+2z+3?2i][z?3?2i]

?被积函数的四个单极点中，只有z0=±3?22i在积分回路内，其留数分别为

Resf(

3?22i)=lim3?22i)=lim

z→z0

2[z+3+2z+3?2i]z

2[z+3+2z?3?2i]

,81.82

Resf(?

z→z0

I=2πi·

11π·=.i42Bxiangap@sina.comT85966382DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?

AllRightsReserved

第四章留数定理21

2.计算下列实变函数定积分．

(1)?∞x2+1?∞dx.

解：

z2+1z2+1f(z)=4=z+1(z2+i)(z2?i)

=[z?(1?i)][z+(1?i)][z?(1+i)][z+(1+i)]

√√?(1?i),(1+i)在上半平面，其留数分别为z2+1它具有四个极点，其中只有z0=

????√212z+1?=,(i?1)=lim?Resfz→z022i(z2+i)z?(1?i)????√z2+11??=,Resf(i+1)=limz→z022i(z2+i)z+(1?i)?√11+I=2πi·=2π.2i2i?

本题和下面几题都属于类型二，方法类似．

(2)?∞0x2dx.

解：由于被积函数是偶函数，所以

?∞

被积函数0x2dx1=(x+9)(x+4)2?∞?∞x2dx,(x+9)(x+4)z2z2

=,(z+9)(z+4)(z+3i)(z?3i)(z+2i)(z?2i)它在上半平面有两个奇点，一个是极点z0=3i，一个二阶极点z0=2i，其留数分别为

?3z2

=i,Resf(3i)=limz→3i(z+3i)(z2+4)250?

??dz2

Resf(2i)=limz→2idz(z2+9)(z+2i)2

??2z2z3(z+2i)2+2z2(z2+9)(z+2i)=lim?z→2i(z2+9)(z+2i)2[(z2+9)(z+2i)2]2

13=?i,200

??13i13iπI=2πi·?=.250200200

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

22§4.2应用留数定理计算实变函数定积分

3.计算下列实变函数定积分．(1)?∞

xsinx?∞dx.

解：因被积函数是偶函数，所以

?∞

xsinxxsinx

dx=2dx.221+x1+x0?∞

zeizziziz

上式的中被积函数G(z)e=e=在上半平面有一个单极点z0=i，且

∞

Resf(i)=lim

z→i

zz+i12e

eiz=π.e

1.2e

I=π·2=

(2)

?∞

cosmxdx.

解：被积函数

eimzeimz

F(z)e=2=

(z+a2)2(z+iα)2(z?iα)2

在上半平面上只有一个二阶极点z0=iα，其留数为

imz

??deimz

Resf(ai)=lim

z→iαdz(z+iα)2

??imeimz2eimz

=lim?z→iα(z+iα)2(z+iα)3(αm+1)e?mα=?.

4α3

π(αm+1)e?mα(αm+1)e?mα

i=.I=πi?

4α34α3

?∞

(3)

eimx

?∞dx,

eimx

?∞dx,(m>0,Reα>0).

imz

解：在上半平面上，fraceimzz?iα有单极点z0=iα，e无奇点，所以

∞

?∞

eimx

dx=2πilimeimz=2πie?mα,

z→iαx?iα

∞

?∞

eimx

dx=0.x+iα

c2003–XiangAnping?

AllRightsReserved

Bxiangap@sina.comT85966382DepartmentofOptoelectronics

ChengduUniversityofInformationTechnology

第四章留数定理Bxiangap@sina.comT85966382§4.3计算定分的补充例体DepartmentofOptoelectronicsChengduUniversityofInformationTechnology23?c2003–XiangAnpingAllRightsReserved

第五章傅里叶变换

§5.1

傅里叶级数

1.交流电压E0sinωt经过全波振流，成为E(t)=E0|sinωt|．试将其展为傅里叶级数．解：交流电压E0sinωt在区间?π≤ωt≤π上是一个周期，令ωt=x，则经过振流后成为：

E(x)=a0+

其中系数

∞?k=1

(akcoskx+bksinkx),

?π?

1E0π

f(x)dx=sinxdxa0=

2π?ππ0

?π2EE0?0

=(?cosx)?=

0ππ

ak=

π=====

当k=1时，

f(x)coskxdx

?π0

?1π1

E(?sinx)coskxdx+E0sinxcoskxdxπ?ππ0?2π

E0sinxcoskxdxπ0?

2πE0

[sin(kx+x)?sin(kx?x)]dx

π02

??πE0cos(k+1)xcos(k?1)x??πk+1k?10?

0,(当k为奇数时,但k?1).4E0

(当k为偶数时).,?

0π

a1=

又令k=2n时，则

E0sinxcosxdx=

sin22xdx=0,

ak=a2n=

同理，可以计算的bk

1bk=

所以

E(t)=a0+

∞?n=1

4E0

,n=1,2,3,···

π(1?4n2)

0π

?π

f(x)sinkxdx=

E0sinxsinkxdx=0.

∞?n=1

ancos2nx=a0+ancos2nωt

∞

2E04E0?cos2nωt=+.

ππn=11?4n2

Bxiangap@sina.com

T85966382DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?

AllRightsReserved

第五章傅里叶变换25

2.将锯齿波展为傅里叶级数．在(0,T)这个周期上，该锯齿波可表为f(x)=x/3．

解：锯齿波之周期为T．令

2l=T,

得

T,2将l代入以2l为周期之傅里叶级数和傅里叶系数表达式即可得适合本题傅里叶级数和傅里叶系

数表达式：l=f(x)=a0+

傅里叶系数的计算如下：

??1T1T1a0=f(t)dt=x·dxT0T03

112?T=·x?T=,03T26∞??n=12nπ2nπancost+bnsintTT?.

2an=T

2=T

应用积分公式：

???0Tf(t)cosT2nπtdtT012nπxcosxdx,3T

xcosPxdx=?21xcosPx+sinPxP2P?T

an=211x2nπ2nπcos·x+sinxT3TT0??2??TT2nπ2nπ2nπ2=cosx+xsinx3T2nπTTT0

=0,

?2nπ2T12nπf(t)sintdt=xsinxdxTT3T00?T?2nπ2nπ21x1=·x?cosx2nπsinT3TT0??2??TT2nπ2nπ2nπ2=sinx?xcosx3T2nπTtT0

T=?,3nπT2bn=T?

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

26§5.1傅里叶级数

T?T2nπf(x)=?sinx.6n=13nπT

3.将下列函数展为Fourier级数．

(1)f(x)=cos3x.

解：可按书上的标准方法展开．此外，还可令t=eix后把f(x)化为t的有理分式，展为Taylor级数后再将变数换回x．

?ix??ix3e+ef(x)=cos3x=2

?1?i3x=e+3eix+3e?ix+e?i3x

3eix+e?ix1ei3x+e?i3x

+·=·4242

31=cosx+cos3x.44

注：本题其实就是三倍角公式：

cos3x=4cosx?3cosx

所以31cosx+cos3x.44

(2)在(?π,π)这个周期上，f(x)=cosαx，(α非整数)．f(x)=cos3x=解：因为f(x)是偶函数，所以bk=0，

f(x)=a0∞?

k==1∞akcoskx.

a0=ak======?π?π11sinαπ?cosαξdξ=sinαξ?=.?π2π?π2απαπ?2πcosαξcoskξdξπ0??1π1πcos(k+α)ξdξ+cos(k?α)ξdξπ0π0??π1sin(k+α)ξsin(k?α)ξ+πk+αk?α0??1sin(k+α)πsin(k?α)π+πk+αk?α11[sinkπcosαπ?coskπsinαπ]·πk+α11[sinkπcosαπ?coskπsinαπ]+·πk?α??111coskπsinαπ?πk+αk?α

c2003–XiangAnping?

AllRightsReservedBxiangap@sina.comT85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnology

第五章傅里叶变换27

1?2α(?1)ksinαπ·2πk?α2

(?1)k+12α=sinαπ·.πk?α=所以?∞k+1?2sinαπ1α(?1)f(x)=+coskx.π2αk=1k2?α2?4要求下列函数f(x)的值在它的定义区间的边界上为零，试根据这一要求将f(x)展为Fourier级数．

(1)f(x)=cosαx，定义在(0,π)上．

解：按题意，在边界(0,π)上，f(0)=0和f(π)=0，由此可知，展开式中只有正弦项，即ak=0，因而展开式可表为∞?f(x)=bksinkx,

其中

应用三角公式

可得

bk====

所以2cosαxsinkx=sin(k+α)x+sin(k?α)x?π??1sin(k+α)x+sin(k?α)xdxπ0?π1?(?1)?π1?(?1)cos(k+α)x+cos(k?α)x00πk+απk?α?1?11?1?1?cos(k+α)π+1?cos(k?α)ππk+απk?α??2kk+11+(?1)cosαπ.π(k2?α2)∞?k?2?k+1f(x)=1+(?1)cosαπsinkx.πk=1k?αk=12bk=π?0πcosαxsinkxdx.2sinαcosβ=sin(α+β)+sin(α?β)

(2)f(x)=1，定义在(0,π)上．

解：因为要满足f(0)=0和f(π)=0，则展开式中只有正弦项．

∞?f(x)=bksinkx,

k=1

其中，??π2π2?

bk=sinkξdξ=?coskξ0π0kπ

?2?2?=?coskπ+1=1?coskπ]kππ?0(k=2n),=4(k=2n+1).,

DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReservedBxiangap@sina.comT85966382

28§5.2Fourier积分与Fourier变换所以

4?1f(x)=sin(2n+1)x.πk=02n+1∞

§5.2Fourier积分与Fourier变换

?t1?1.求单个锯齿脉冲f(t)=ktrect?，即

??0,

f(t)=kt,?0,(t<0)(0<t<T)(t>T)

的Fourier变换

解：因为f(t)是无界空间中的非周期函数，它的周期为∞，故可展开为Fourier积分，其Fourier变换：?∞?∞

f(t)=A(ω)cosωtdω+B(ω)sinωtdω

其中Fourier变换A(ω)和B(ω)为：

??1∞1T

A(ω)=f(x)cosωxdx=ktcosωtdtπ?∞π0?Tk=ωtcosωtd(ωt)πω0

?Tk?cosωt+ωtsinωt=0πω2

k=[cosωT+ωTsinωT?1],πω2

??1T1∞

B(ω)=f(x)sinωxdx=ktsinωtdtπ?∞π0

?Tk?=sinωt?ωtcosωt0πω2

k[sinωT?ωTcosωT],=πω2

复数形式为：???1??iωTke?1+iTe?iωT.2πωω

πt2.求sinct=sin

的Fourier变换，试以本题的Fourier变换函数跟图5-1比较，又以本题的

sinct跟图5-2比较，比较的结果说明什么问题？

解：因sinπt和πt是奇函数，所以sinct是偶函数，应展为Fourier余弦积分，其余弦Fourier变换为?2∞sinπξA(ω)=cosωξdξπ0πξ?2∞1=2sinπξcosωξdξπ0ξ??∞??∞111=2sin(ω+π)ξdξ?sin(ω?π)ξdξπξξ00Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第五章傅里叶变换29

dξ=0?=

1?dξ+dξ=??x?1??

??>x10?x???=rect=1

??<1π2π?

∞sinξ0??∞sinξ1

01??

dξ?

?∞

sinξ0?∞sinξ0?

(ω>π)(ω<π)

如果不考虑常数因子，本题的Fourier变换函数的图像跟图5-1相同；以本题的sinct的图

象跟图5-2也相同．这是由于Fourier积分和Fourier变换式对变数ω和x是对称的，亦即sinct和rect(x/2π)互为Fourier变换，可以说rect(x/2π)是sinct的Fourier变换式，也可以说sinct是rect(x/2π)的Fourier变换式.

3.把下列脉冲f(t)展为Fourier积分，

??0????h

f(t)=

?h???0

(t<?T),

(?T<t<0),(0<t<T),(T<t).

注意在半无界区间(0,∞)上，本例的f(t)跟例1的f(t)相同．解：因为f(t)是奇函数，所以可展开为Fourier正弦积分：

?∞

f(t)=B(ωt)sinωtdω

其Fourier变换为：

??2T2hT

B(ω)=hsinωξdξ=sinωξd(ωξ)

π0πω0

2h2h?(?cosωξ)?=(1?cosωT).=

0πωπω

∞

所以

f(t)=

(1?cosωT)sinωtdω.πω

4.f(t)是定义在半无界区间(0,∞)上的函数，

?h(0<t<T),

f(t)=

0(T<t).(1)在边界条件f?(0)=0下，把f(t)展开为Fourier积分；(2)在边界条件f(0)=0下，把f(t)展开为Fourier积分．

解：（１）要满足边界条件f?(0)=0，必须将f(t)展为Fourier余弦积分．?∞

f(t)=A(ω)cosωtdω,

其中

2T2∞

f(ξ)cosωξdξ=hcosωξdξA(ω)=

π0π0

2h2h?=sinωξ?=sinωT.

0πωπω

所以

f(t)=

∞

2h2h

sinωTcosωtdω=πωπ

∞

sinωTcosωtdω

c2003–XiangAnping?

AllRightsReserved

Bxiangap@sina.comT85966382DepartmentofOptoelectronics

ChengduUniversityofInformationTechnology

30§5.3δ函数

（２）要满足边界条件f(0)=0，必须将f(t)展为Fourier正弦积分．?∞

f(t)=B(ω)sinωtdω,

其中

所以

.??2∞2TB(ω)=f(ξ)sinωξdξ=hsinωξdξπ0π0?T2h2h?=(?cosωξ)?=(1?cosωT).0πωπω??∞2h∞(1?cosωT)sinωtdω2h(1?cosωT)sinωtdω=f(t)=πωπ0ω0

§5.3δ函数

1.验证§5.2例2的频谱B(ω)(图5-4)于N→∞时就成为Aδ(ω?ω0)?Aδ(ω+ω0)，并解释这结果的物理意义．

解：因为??2Aω0ωsinB(ω)=N2πω)π(ω2?ω00????ωωAsin0N2πAsin0N2π=?πω?ω0πω+ω0????2πN2πNAsin0(ω?ω0)Asin0(ω+ω0)?=πω?ω0πω+ω0

当N→∞时，即→∞，这时有限正弦波列成为无限正弦波列．而????2πN2πN1sin0(ω?ω0)1sin0(ω+ω0)B(ω)=Alim?AlimN→∞πN→∞πω?ω0ω+ω0

=Aδ(ω?ω0)?Aδ(ω+ω0).

lim2πN01sinkx=δ(x).k→∞πx

所以，对于无限正弦波列，它的频谱成为两条线，一条位于ω=ω0处，另一条位于ω=?ω0处，振动成为单一圆频率ω的振动．

2.把δ展为实数形式的Foruier积分．

解：因为δ是偶函数，它的Foruier积分可表示为：?∞

δ(x)=A(ω)cosωxdω,

0所以

而

所以?1∞A(ω)=δ(x)cosωxdxπ?∞11=cos(ω·0)=.ππ?1∞

δ(x)=cosωxdω,π0

DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReservedBxiangap@sina.comT85966382

第五章傅里叶变换或

Bxiangap@sina.comT85966382?∞δ(x)=1eiωx2πdω?∞=1??∞?∞?2πcosωxdω+isinωxdω?∞=1??∞∞?2πcosωxdω=1∞cosωxdω.?∞π0DepartmentofOptoelectronicsChengduUniversityofInformationTechnology31?c2003–XiangAnpingAllRightsReserved

第六章Laplace变换

§6.1符号法

无作业

§6.2Laplace变换

1.求下列函数的Laplace变换函数．

(1)shωt,chωt.

解：(a)

?(t)=shωt=1?

2eωt?e?ωt?

?1?11?

2p?ω?p+ω=ω

p?ω(b)

?(t)=chωt=1?eωt+e?ωt?

?111?ω

2p?ω?p+ω=p2?ω2

(2)e?λtsinωt,e?λtcosωt

解：(a)

?(t)=e?λtsinωt=1e?λt?eiωt?e?iωt?

?2i?

?11

2i(p+λ)?iω?1

(p+λ)+iω

=ω

(p+λ)2+ω2.

(b)

?(t)=e?λtcosωt=1?λt?

2eeiωt+e?iωt?

?1?11?2(p+λ)?iω+(p+λ)+iω

=p+λ

(p+λ)+ω.

?(3)1

解：

?(t)=1

?∞

(p)=1e?ptdt,

0Bxiangap@sina.comDepartmentofOptoelectronicsT85966382ChengduUniversityofInformationTechnology?c2003–XiangAnpingAllRightsReserved

第六章Laplace变换33若令t=x2,dt=2xdx，则

(p)=?

0∞

====(4)δ(t?τ).

解：?∞22e?pxdx0?∞122√e?pxd()0?∞22e?ydy0√21·=.211?px2e·2xdxx?

L[δ(t?τ)]=eL[δ(t)]=e

0?+∞

=e?pτδ(t)e?ptdt

?∞?=e?pτe?pt?t=0=e?pτ?pτ?pτ∞δ(t)e?ptdt

§6.3

1.把下列像函数反演

(1)p)=6

,Laplace变换的反演

解：由位移定律得

3!?t3e?t

(3+1)(p+1)

(2)p)=解：3p3=p2?12(3)p)=

解：

1?e2t=y(t),p?2

3?3e2t=z(t).p?2

(4)p)=

解：

224t?te(p?1)(4+1)4!

2.求(p)=Lp2+Rp+E2.1,3p.?11+p+1p?1?3?(e?t+et)=3cosht.2注意：cosht=cht称为双曲余弦．p)=3.的原函数．

DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReservedBxiangap@sina.comT85966382

34§6.3Laplace变换的反演

解：

p)=

RER2.

R2Lp++?

1p+

R??

1(1)如果R2?

4L=0，则

(p)=

E1ELP+R?te?Rt

=j(t).L

(2)　如果R2?

4L>0，则

(p)=

1Lp+R2

?R2

1?E

?Rt

sinh

R2L

R2?

14L2?1

t.(3)　如果R2?

4L<0，则

(p)=

1Lp+R2?1?

R2?

?Rt

R2e

sin

1Lc?R24L2

t.?

3.求(p)=λ?p的原函数．解：

p)=

λ?p+CC?

(p+C)4?

(p+C)4?=λ?

(p+C)?C

(p+C)?y(t)=

L[p)]=λ?1?2?CtC3?Ct

2!te?te

3!λ?e?Ctt2?Ct323

.4.求下列像函数的原函数．

(1)(p)=π1,

(2)(p)=π,(3)(p)=

1,(4)(p)=

π.

解：

(1)I(t)=π?at2πae.(2)I(t)=2.(3)

p)=π?1

2p?

p+1

,I(t)=π?

1?e?t?2.(4)

I(t)=

π2

t.Bxiangap@sina.comDepartmentofOptoelectronics

T85966382ChengduUniversityofInformationTechnology

c2003–XiangAnpingAllRightsReserved

第六章Laplace变换35

§6.4

1.求解下列常微分方程．

(1)d3y

ydy?t+3d+3+y=6e,y(0)=2应用例d2y?t=0dy?t=0?=?=0.

解：对该方程施行Laplace变换，得

(p)=然后再求出p)的原函数为

y(t)=t3e?t.

这就是该常微分方程的解．

(2)d2y

6,(p+1)4+9y=30cosht,y(0)=3,y?(0)=0.

3p,p2?1解：对该方程施行Laplace变换，得(p)=

然后再求出p)的原函数为

y(t)=3cosht,

此即该常微分方程的解．

2.电压为E的直流电源通过电感L和电阻R对电容C充电．求解充电电流j的变化情况．解：设电键Ｋ关闭前电路中无电流，即j(0)=0．电键Ｋ闭合后电流j所满足的微分方程是?dj1t

L+Rj+jdt=E.dtC0

结合初始条件j(0)=0对上述方程施行Laplace变换后，得11ELp(p)+R(p)+·p)=,Cpp

1Lp2p)+Rp(p)+(p)=E,CE(p)=.2Lp+Rp+然后再求出p)的原函数为

(1)如果R2?4L

=0，则

j(t)=E?Rtte.L

?(2)如果R2?4L

>0，则

j(t)=LER2

?1e?RtsinhR21?t.4L2LC

(3)如果R2?4L

<如果0，则

j(t)=LE1

??R2

e?Rtsin1R2?t.LC4L2

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第二篇数学物理方程

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第七章数学物理定解问题37

第七章数学物理定解问题

本章介绍一些常见的数学物理方程定解问题的导出，并简要叙述方程的分类．

（一）导出方程的一般方法

下面所涉及的方程主要是二阶的线性偏微分方程．导出这些方程的一般方法是：在选定表征物理过程(或状态)的物理量后，从体系内部划出微小的一块，应用基本的物理规律考察这一小块的运动、变化或平衡状态，最后令此小块的体积趋广零．有时这种方程也可以从基本物理方程直接推演而得．对于振动（波动）过程、方程还可以利用哈密顿原理变分而得．

（二）定解问题

具体物理过程(状态)的确定不仅依赖于方程、还依赖于体系所处的周围环境和历．史换句话说，物理量的确定还依赖于它本身或它的外法向导数或者两者的线性组合在区域边界上的取值和开始时刻它的取值．前者称为边界条件．后者称为初始条件，合称定解条件．数学物理方程附以合适的定解条件构成一个定解问题．一个定解问题的解应是唯一的(至多含有一个附加的常数项)．

(三)初始条件、三类边界条件和衔接条件的确定

以函数u(r,t)=u(x,y,z,t)表示表征物理过程(或状态)的物理量，其中r=(xyz)是空间变量，t是时间变量．当方程中出现的关于自变量的偏导数的最高阶数是二阶时．称此方程是二阶的．如果方程所含的关丁l的偏导数的最高阶数是二阶，则所需的初姑条件是

§7.1数学物理方程的导出

1.拿图7-7的Ｂ段弦作代表，推导弦振动方程．

解：取x到x+dx的Ｂ段弦，这段弦无纵向振动，所以纵向合力为零，

T2cosα2?T1cosα1=0.

Ｂ段弦的横振动方程为

T1sinα1?T2sinα2=uttρds.

在小振动的情况下，有α1≈α2≈0,cosα1≈cosα2≈1,√du≈0,ds=dx2+du2≈dx,

sinα1≈tgα1,sinα2≈tgα2,

如题文图所示，

tgα1=?ux|x,tgα2=?ux|x+dx,

故在小振动的情况下，运动方程为?T1=T2,

T2ux|x+dx?T1ux|x=uttρdx,

即

上式左边即

所以，令a2=T

，有

这就是所求振动方程．???u?u??TT?x+dxx=ρutt,dx?ux?2uT=T2?x?xutt?a2uxx=0.

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

38§7.2定解条件

§7.2定解条件

1.长为l的均匀弦，两端x=0和x=l固定，弦中张力为T0，在x=h点，以横向力F0拉弦，达到稳定后放手任其自由振动．写出初始条件．

解：设横向力F0作用处弦的位移为（最大）C，则弦的初始位移为

?C?x,(0≤x≤h),u?t=0=C(h≤x≤l).(l?x),

在力F0作用点处，所受力平衡，所以

T2cosα2?T1cosα1=0

F0?T2sinα2?T1sinα1=0

因为是小振动,所以

sinα1≈tanα1≈α1,

cosα1≈1,

代入力的平衡方程中，得

T2=T1=0

CCF0=T0+T0hl?h

解得

所以

?u?t=0?sinα2≈tanα2≈α2cosα2≈1F0h(l?h)T0l,,(0≤x≤h),(h≤x≤l).F0(l?h)0x

F0h

0(l?x)

初始速度为

?u?t=0=0.

2.长为l的均匀杆两端受力F0作用而纵振动．写出边界条件．

解：杆两端所受的拉力F0等于这两端面所受的杨氏弹性力

?u??u???YS?=?YS?=?F0,?nx=0?xx=0??u?YS?=F0.?xx=0??u??u??YS?=YS?=F0.?nx=l?xx=l

3.长为l的均匀杆，两端有恒定热流进入，其强度为q0，写出这个热传导问题的边界条件．

解：在边界上有

?u???k?=qn,?nΣ

DepartmentofOptoelectronics

ChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReservedBxiangap@sina.comT85966382

第七章数学物理定解问题39在x=l端,?u??u????k?=?k?=qn=?q,?nx=l?xx=l即?u??k?=q.?xx=l在x=0端，?u??u????k?=k?=qn=?q,?nx=0?xx=0即?u??k?=?q.?xx=0

4.习题1是否需要衔接条件？

解：弦在振动时，F0已不起作用，所以不需要衔接条件，若弦在振动时，力F0仍然在起作用，就要衔接条件．

5.一根杆由横截面相同的两段连接而成，两段的材料不同，杨氏模量分别为YI、YII，密度分别为ρI、ρII，试写出衔接条件．

解：设两段杆的接点为x=0，在连接处位移u是连续的，所以有

I?I?I?u?I?u?YS?=YS?,?nx=0?xx=0

II?II?II?u?II?u?YS?=YS?.?nx=0?xx=0这两力是作用力与反作用里，所以

II?I?II?u?I?u?YS?=YS?.?xx=0?xx=0

这就是衔接条件．

6写出静电场中电介质表面的衔接条件．

解：在电介质表面，电势是连续的．??uI?x?0=uII?x+0,

又电位移法向分量连续，

D=ε1E1=ε2E2

即

?uI??uII???ε1?=ε2?.?xx?0?xx+0

§7.3

无作业数学物理方程的分类

§7.4

解：定解问题为：达朗贝尔公式定解问题1求解无限长弦的自由振动，设弦的初始位移为?(x)，初始速度为?a??(x)．?2?auxx=0?utt?u??=?(x),t=0??utt=0=?a??(x).?∞<x<+∞,

这是一个一维无界空间的问题，根据达朗贝尔公式，有

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

40§7.4达朗贝尔公式定解问题

?x+at?11?u(x,t)=?(x+at)+?(x?at)+ψ(ξ)dξ22ax?at

将初始位移和初始速度代入上式，得?x+at?11?u(x,t)=?(x+at)+?(x?at)+?a??(ξ)dξ22ax?at??1x+at?1??(ξ)dξ=?(x+at)+?(x?at)?22x?at

?11?1=?(x+at)+?(x?at)??(x+at)+?(x?at)222

=?(x?at).

?2.无限长弦在点x=x0受到初始冲击，冲量为I，试求解弦的振动．［提示：u?t=0=

(I/ρ)δ(x?x0)］．波只朝一个方向（x正向）传播，是一列行波．

解：定解问题为：???I22??auxx=0,?∞<x<∞,其中a=,?utt?=0,u??t=0???II?utt=0=δ(ξ?x0)=H(ξ?x0).

??1x+atIu(x,t)=∞δ(ξ?x0)dξ2ax?atρ?x+atIH?(ξ?x0)d(ξ?x0)=2aρx?at

??x+atIH(ξ?x0)x?at=2ρT

I[H(x?x0+at)?H(x?x0?at)].2?3.半无限长弦的初始位移和初始速度都是零，端点作微小振动u?x=0=Asinωt．求解弦的

振动．=x解：对于x≥at，显然有u(x,t)=0．下面研究t>，将初始条件延拓到x<0的半无界区

域后，定解问题为??utt?a2uxx=0,?∞<x<∞,???u(0,t)=Asinωt,???0,x≥0,0,x≥0,??u(x,0)=Φu(x,0)=Ψ??(x),0<x,ψ(x),x<0,

其中?(x)和ψ(x)是待定函数．

将达朗贝尔公式用于延拓后的无界弦，有?x+at11u(x,t)=[Φ(x+at)+Φ(x?at)]+Ψ(ξ)dξ,22ax?at

且令其满足边界条件，得?0?11?Asinωt=0+?(?at)+Ψ(ξ)dξ,22a?at?011Asinωt=?(?at)+Ψ(ξ)dξ,22a?at

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第七章数学物理定解问题41记at为x，则?0x11Asinω=?(?x)+ψ(ξ)dξ,a22a?x?ω?显然，若取?(x)=2Asin?x，ψ(x)=0，则

Bxiangap@sina.com

T85966382?u(x,t)=12?(x?at)=Asin?ω?(x?at)?x?a?x?=Asinωt?a.t>a.DepartmentofOptoelectronicsChengduUniversityofInformationTechnology?c2003–XiangAnpingAllRightsReserved

第八章分离变数（傅里叶级数）法

§8.1齐次方程的分离变数法

1.长为l的弦，两端固定，弦中张力为T，在距一端为x0的一点以力F0把弦拉开，然后突然撤除这力．求解弦的振动．

??utt?a2uxx=0,(0<x<l).????(l,t)=0,?u(0,t)=u?Fl?x(0<x<x0),x,?u(x,0)=F0x0??(x0<x<l),?(l?x),???u?=0.tt=0

令u(x,t)=X(x)T(t)代入泛定方程，得

X”T”==?λ2.XaT

由此可得?T”+a2λ2T=0,

X”+λ2X=0,X(0)=X(l)=0.解：定解问题为

由此可得关于X的解是：

X(x)=csinλx

由X(l)=0可知，csinλl=0，c不能为0，否则x≡0．无意义，所以

nπsinλl=0,λ=,(n=1,2,3,···)l??以λ的数值=nπ代入关于T的方程得T的解：

nπanπaTn(t)=Ancost+Bnsint.ll

∞??nπanπa?

T(t)=Ancost+Bnsint,lln=1

u(x,t)=X(x)T(t)

∞??nπanπa?nπ=Ancost+Bnsintsinx.llln=1

将u的表达式代入第二初始条件得：

∞???nπanπanπa?nπ?nπa?utt=0=tsint+Bncostsinx?t=0?Anllllln=1

=∞?

n=1Bnnπanπcos0sinx=0.ll

Bn=0.

则

u(x,t)=∞?

n=1Ancosnπnπatsinx.ll

c2003–XiangAnping?

AllRightsReservedBxiangap@sina.comT85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnology

第八章分离变数法43根据第一初始条件，有：?F0l?x0?∞??xnπTlu(x,0)=Ansinx=Fx?l?00(l?x)n=1Tl

?2lnπAn=?(ξ)sinξdξl0l??2x0F0l?x0nπ2lF0=ξsinξdξ+l0Tlllx0T

nπx02F0l1·sin=Tπ2n2l(0<x<x0),(x0<x<l).x0nπ(l?ξ)sinξdξll

u(x,t)=∞?

n=1Ancosnπatsinnπlxl

∞2F0l?1nπx0nπnπa=sinsinxcostTπ2

n=1n2lll

2.求解细杆导热问题，杆长l，两端保持为零度，初始温度分布

?bx(l?x)u?t=0=.l2

解：定解问题为??2?a2=?ut?auxx=0,???ux=0=u?x=l=0,???u?t=0=bx(l?x)/l2.?k(0≤x≤l),

设

u(x,t)=X(x)T(t)

代入泛定方程有

由此得到T?X??==?λa2Tx

?2T+aλT=0.?X??+λX=0,

X(0)=X(l)=0.

解X得

X(x)=A?ncos由边界条件得

n2π2

λ=,l

X(x)=B?nsin

解关于T的方程

?Tn√√λx+B?sinλx,nn=1,23···.nπx.ln2π2a2+Tn=0,l2

?n2π2a2

lTn=Cnet,

c2003–XiangAnping?

AllRightsReservedBxiangap@sina.comT85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnology

∞?

n=1?n2π2a2l§8.1齐次方程的分离变数法tu(x,t)=

由初始条件得

u(x,0)=∞?

n=1Bnesinnπx.lBnsinnπbx(l?x)x=,ll2

8b,(当n为奇数n=2k+1时),3(2k+1)3π=?0.(当n为偶数时).

∞?

k=0

∞(2k+1)2l??u(x,t)=Bke?π2a2tsin(2k+1)πxl2228b?1(2k+1)π?(2k+1)

πat=3ex.sinπk=0(2k+1)3l

3.两端固定弦，长为l，（１）用宽为2δ的平面锤敲击弦的x=x0点．（２）用宽度为2δ的余弦式凸锤敲击弦的x=x0点．求解弦的振动．

解：（１）若锤为平面锤，定解问题为?2?u?auxx=0,(0<x<l),?tt??????????u?x=0=ux=l=0,

u?t=0=0,??????0,(0<x<x0?δ,x0+δ<x<l),???u=??tt=0v0,(x0?δ<x<x0+δ).

根据边界条件，可知本征函数为sinnπx，故弦的一般振动可表示为

u(x,t)=

因此，代入初始条件的

u(x,0)=∞?

n=1

∞?nπanπxut(x,0)=Bnsin=ln?n=1∞??n=1nπanπat?nπxAncos+Bnsinsin,lllAnsinnπx=0.l?0,(0<x<x0?δ,x0+δ<x<l),(x0?δ<x<x0+δ).

nπξdξ,lv0,l由此解得Fourier系数2An=l?00·sin?x0+δ2nπξBn=v0sindξnπax0?δl

4v0lnπx0nπδ=22sinsin,nπall

∞nπx0nπδnπatnπx4v0l?1u(x,t)=sinsinsinsin.aπ2

n=1n2llll

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第八章分离变数法45

（２）若为余弦式锤，则定解问题为??utt?a2uxx=0(0<x<l),??????u(0,t)=u(l,t)=0,??u(x,0)=0,????0,?(0<x<x0?δ,x0+δ<x<l),???ut(x,0)=?x?x0??v0cos?π,(x0?δ<x<x0+δ).2δ

x根据边界条件可知本征函数为sinnπ，因而弦的一般解可表示为

∞??nπatnπat?nπxu(x,t)=Ancos+Bnsinsin,llln=1

代如初始条件得

nπx=0,ln=1?

∞?nπanπx?0,ut(x,0)=Bnsinx?x0?v0cosllπ,n=12δ

由上二式解得u(x,0)=Ansin

An=0,∞?(0<x<x0?δ,x0+δ<x<l),(x0?δ<x<x0+δ).?x0+δ2x?x0nπxBn=v0cosπsindxnπax0?δ2δl

1nπx08v0δnπδ=cos,2δnsinnπa1?llu(x,t)=8v0δ

aπ2∞?

n=11·nnπx01nπδnπatnπxcossinsin.2sinllll2δn1?l

4.长为l的杆，一端固定，另一端受力F0而伸长．求解杆在放手后的振动．

解：定解问题为

?utt?a2uxx=0,(0≤x≤l),??????u(0,t)=ux(l,t)=0,?x?xF0F0x?u?dx=dx=,u(x,0)=???xYSYS?00??ut(x,0)=0.(0≤x≤l),

本题是既有第一类边界条件也有第二类边界条件的问题，令

u(x,t)=X(x)T(t)

代入泛定方程得

?T??+λa2T=0,

X??+λX=0,

X(0)=X?(l)=0.

（１）若λ<0，则只能得到x≡0的无意义解．

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

46§8.2非齐次振动方程和输运方程

（２）若λ=0，也只能得到x≡0的无意义解．

（３）仅当λ>0时才能得到有意义的解．??21n+π2

2λ=,l2??1n+2πx.Xn(x)=Csinl

代本征值入T的方程得????11n+n+22?Tn(t)=A?cosaπt+Bsinaπt,nnll????????111n+n+n+∞???222?sin?Ancosu(x,t)=aπt+Bsinaπtπx.n??llln=0

利用第二初始条件得

Bn=0.

再利用第一初始条件得?1n+∞?F02πx=x,AnsinlYSn=1??1?n+2lF02An=ξsinπξdξl0YSl

2lF0(?1)n.=2YS12n+π2

????11n+aπtn+πx∞8lF0?(?1)n22u(x,t)=2cossin.πYSn=0(2n+1)2ll?

§8.2

无作业非齐次振动方程和输运方程

§8.3

无作业非齐次边界条件的处理

§8.4Poisson方程

无作业

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

第九章二阶常微分方程的级数解法本征值问题47

第九章二阶常微分方程的级数解法本征值问题

§9.1

解：二维波动方程为

utt?a2?2u=0

先把时间变数分离出来，设分离形式的解为

u(ρ,?;t)=U(ρ,?)·T(t)

代入式()，有

U(ρ,?)·T??(t)?a2U(ρ,?)·T(t)=0,

T???2U=.a2TU

上式左边仅是t的函数，右边是ρ和?的函数，若要等式成立，除非两边为同一常数，记为?k2，有

T??+a2k2T=0(9-2)

?2U+k2U=0

式（）为二维Helmholtz方程，在平面极左边系下的表达式为

11Uρρ+Uρ+2U??+k2U=0.ρρ

进一步分离变数，令

U(ρ,?)=R(ρ)Φ(?)

并代入上式得

11R??(ρ)Φ(?)+R?(ρ)Φ(?)+2R(ρ)Φ??(?)+k2R(ρ)Φ(?)=0ρρ

由此得

Φ??ρ2R??ρR?22++kρ=?.RRΦ

同理，等式两边应为同一常数，记为m2，得

Φ??+m2Φ=0,

ρ2R??+ρR?+(k2ρ2?m2)R=0.

对方程（）作变数代换x=kρ后变为Bessel方程

x2R??+xR?+(x2?m2)R=0.

方程（）和自然周期条件Φ(?)=Φ(?+2π)一起构成本征值问题，其解为

m=0,1,2,3,······.

Φm=Amcosm?+Bmsinm?,(9-6)(9-4)(9-5)(9-3)(9-1)特殊函数常微分方程1.试用平面极坐标系把二维波动方程分离变数．

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

48§9.2常点邻域上的级数解法方程（）的解为

Tk=Ckcoskat+Dksinkat.

2.试用平面极坐标系把二维输运方程分离变数．

解：二维输运方程为

ut?a2?2u=0

在平面极坐标系下方程（9-1）为

ut?a2?(9-1)?11uρρ+uρ+2uρρρρ=0,(9-2)

令u(ρ,?;t)=R(ρ)Φ(?)T(t)，代入方程（2）中，整理得

R??1R?1Φ??T?

=++=?k2.aTRρRρΦ

T?+a2k2T=0,

R??1R?1Φ??

++2=?k2.RρRρΦ

方程（3）可进一步分离变数

R?Φ??22ρ+ρ+kρ=?=m2,RRΦ2R??(9-3)(9-4)

即?Φ??+m2Φ=0,

Φ(?)=Φ(?+2π).

ρ2R??+ρR?+(k2ρ2?m2)R=0.

方程（6）作变数代换x=kρ变成Bessel方程

x2R??+xR?+(x2?m2)R=0.

方程（3）和（5）的解分别为

Tk=Ake?akt,

Φm=Bmcosm?+Cmsinm?.22(9-5)(9-6)(9-7)(9-8)(9-9)

§9.2常点邻域上的级数解法

以下章节作业均不要求，但简单的例题应当掌握

Bxiangap@sina.com

T85966382DepartmentofOptoelectronicsChengduUniversityofInformationTechnologyc2003–XiangAnping?AllRightsReserved

相关推荐

数学物理方法教学大纲

第二篇：数学物理方法答案-部分

专栏推荐