以物易物教案

教学目标：

l．在实践活动中，感受现实生活与数学之间的联系。

2．渗透价值意识，使学生能够合理的、有计划的进行价值分配。

3．培养学生养成节约的好习惯。

活动准备：

要求每位学生从家中带一些以前曾阅读过的书籍或使用过的学习用品和玩具等。

教学过程：

一、故事导入

师：同学们有没有听说过一个故事，用一个小小的回形针换一幢别墅，你们想不想听？ 讲述回形针换别墅的故事，幻灯片出示换的过程 用一个巨型红色万字夹→鱼形钢笔→陶瓷门把手→烤炉→发电机→古董啤酒桶→旧雪车→旅行→开篷车→录制唱片合同→一座复式别墅。你们听了这个故事有什么想法？

师：那什么是以物易物呢？就是指用自己已有的物品/服务与别人交换，以换取别人的物品/服务，是一种现有贸易模式出现之前已有的交易方式。早于人类会使用货币作买卖之前，人类已经懂得以物易物。以物换物不同于买卖，并没有使用任何金钱作交易的工具，所以以物易物不一定是一场等价交换。在7000年前，在河姆渡文化遗址，考古就发现了这个现象，而在中国，历史上第一位以物易物经商贸易的商人源于商丘。

同学们，你们今天都从家里带来了许多好看的图书，还有一些学习用品和有趣的玩具。这些物品你已经看过、使用过，对于你来说使用价值已经不高了，但或许别的同学还需要它。今天我们在这里将要开办一个交易市场，在这个交易市场里，你可以把你带来的各种物品与其他同学带来的物品进行交换，交换到你们自己想要的物品。

二、活动前指导

l．明确怎样交换。

①师：你认为应该怎样交换呢？分小组讨论交换的方法和在交换中应注意些什么？ ②汇报小组讨论情况。

师：说说你准备怎样进行交换？（示范交换过程）

一位同学上台前展示自己的物品，说：“我带来的是一本《安徒生童话故事》，原价是18元，我看了有一年时间，就给这本书打八折，现价是14.40元，这本书陪我渡过了许多日日夜夜，那些精彩而神奇的故事给我带来了许多美好的遐想。有谁愿意将自己的东西和我交换呢？”

师：“同学们觉得她这本书还有哪些好处，或者是哪些特点？”

通过同学的介绍，愿意者可以站起来，陈述自己愿意交换的物品名称、现价及它的好处，这时再看双方是否对对方的东西感兴趣。如果双方都愿意则交换成功，不愿意则交换失败，再重新寻找合适的物品交换。

生：老师你说过在交换过程中要本着等价交换的原则，刚才是一件换一件，我认为也可以一件换几件。

比如刚才那本书价值是14.40元，我想用我的价值为5元的笔记本和9元的铅笔盒两件去交换。

师：你说得很好。交换方法可以是一件换一件，也可以一件换几件，但是在交换过程中应注意些什么？

生：我认为要注意交换的几件物品之间价格尽量不要差距过大。比如原来有一件价值10元的物品，看见一样换一次，换来换去最后换回的物品只值5元，这样就不合适了。

③师：刚才这几位同学讲得非常好，因此大家要做到在交换之前，你非常喜欢的物品，你自己需要的物品，要事先观察、记录，也就是了解市场行情，比较后做到心中有数，全面考虑后再有目的去交换。常言道：“货比三家不吃亏。”其实就是要你精打细算，有目的、有计划地进行交换。有时也并不是一种完全的等价交换,要看自己怎么去看待.如果自己很喜欢一样东西,可以拿另外的东西去换(不再喜欢的),这时候就没有太多的等价交换

三、交易活动开始

l．全面了解物品种类及价格。

师：首先将自己带来的物品放在桌上，然后有秩序地进行市场调查，了解都有哪些东西，哪些是你感兴趣的，而且在价格方面是否能接受等等。

2．开始交换。

师：全面了解之后，回到座位上拿着自己的东西开始有目的进行交换。如果通过市场调查，并没有十分满意的东西，可以观察别人的交换过程。

这时教师可以在活动中了解交易情况，也可以帮助个别在交易中遇到困难的学生进行交换。

四、汇报交易结果

l．了解交换情况。

统计：哪些同学交换成功，获得自己喜欢的东西了？（举手示意）

再请几名学生汇报一下自己的交易情况。

问：在此次交换活动中你是否成功，原因是什么？（请个别学生说说）

2．交换体会。

生1：我在交换过程中，以物易物，应用了等价交换方面的数学知识。

生2：在交换中，我用8元的玩具汽车换了6元的一枝钢笔，虽然在价格上有所差距，但我认为这是我需要的，我就觉得值。

3．教师小结。

除了刚才大家说的这几方面之外，我们的交易活动中也应用了一些简单的心算和估算，同时，对物品的价值也有了一定的理解和判断。根据“物有所值，物有所需”的原则，知道物品的价值取决于个人的爱好和需求，有了自己的价值观。

五、课外拓展

 

第二篇：20xx年高考数学易错题精讲教案二

经典易错题会诊与2014届高考试题预测(二)

考点-2 函数 (1)

函数的定义域和值域

函数单调性的应用

函数的奇偶性和周期性的应用

反函数的概念和性质的应用

借助函数单调性求函数最值或证明不等式

综合运用函数奇偶性、周期性、单调性进行命题

反函数与函数性质的综合

经典易错题会诊

命题角度1 函数的定义域和值域

?f(x)?g(x)?1．(典型例题)对定义域Df、Dg的函数y=f(x)，y=g(x)，规定：函数h(x)=??f(x)

???g(x)当x?Df且x?Dg当x?Df且x?Dg 当x?Df且x?Dg

(1)若函数f(x)=12,g(x)=x，写出函数h(x)的解析式; x?1

(2)求问题(1)中函数h(x)的值域．

[考场错解] (1)∵f(x)的定义域Df为(-∞，1)∪(1，+∞)，g(x)的定义域Dg为R.∴?x2

??x?1

?1h(x)=??x?1

?1??x?(??,1)?(1,??)(x?1)(x?1)

11x2 (2)当x≠1时，h(x)==x-1++2≥4．或h(x)= ∈(-∞，0)∪(0，+∞)． ∴h(x)的值域x?1x?1x?1

为(4，+∞)，当x=1时，h(x)=1．综合，得h(x)的值域为{1}∪[4，+∞]．

[专家把脉] 以上解答有两处错误：一是当x∈Df但x?Dg时，应是空集而不是x≠1．二是求h(x)的值域时，由x≠1求h(x)=x-1+1+2的值域应分x>1和x<1两种情况的讨论． x?1

[对症下药] (1)∵f(x)的定义域Df=(-∞，1)∪(1，+∞)·g(x)的定义域是Dg=(-∞，+∞)．所以，?x2

,h(x)=??x?1?1,?x?(??,1)?(1,??).x?1.

1x2x2?1?1 (2)当x≠1时，h(x)= ==x-1++2． x?1x?1x?1

1

若x>1，则x-1>0，∴h(x)≥2(x?1) 当且仅当x=2时等号成立．

1

+2=4． x?1

若x＜1，则x-1<0．∴h(x)=-[-(x-1)-

1

]+2≤-2+2=0．当且仅当x=0时等号成立． x?1

当x=1时，h(x)=1．

综上，得h(x)的值域为(-∞，0)∪{1}∪[4，+∞]．

2．(典型例题)记函数f(x)=2?

x?3

的定义域为A，g(x)=lg[(x-a-1)(2a-x)](a≤1)的定义域为B. x?1

(1)求A；

(2)若B?A，求实数a的取值范围． [考场错解] (1)由2-x?3x?1

≥0，得≥0，∴x<-1或x≥1，即A=(-∞，-1)∪[1，+∞]． x?3x?1

(2)由(x-a-1)(2a-x)＞0得(x-a-1)(x-2a)<0当a=1时，B=? ．∴B?A．

当a<1时，a+1>2a，∴B=(2a，a+1),

∵B?A，∴2a≥1或a+1≤-1．即a≥或a≤-2而a≤1，∴≤a≤1或a≤-2． 故当B?A时，实数a的取值范围是(-∞，-2)∪[，1].

[专家把脉] 由函数的概念知函数的定义域为非空集合，所以错解中a=1时B= ?，说明函数不存在，

因此 a=1不适合．

[对症下药] (1)由2-x?3x?1

≥0，得≥0， x?3x?1

1

2

1212

∴x<-1或x≥1．即A=(-∞，-1)∪[1，+∞]． (2)由(x-a-1)(2a-x)＞0，得(x-a-1)(x-2a)<0， 当a=1时，B= ?，∵定义域为非空集合，∴a≠1．当 a<1时，a+1>2a，∴B=(2a，a+1)，∵B?A，∴2a≥1或a+1≤-1，即a≥或a ≤-2．而a<1，∴≤a≤1或a≤-2，

故当B?A时，实数a的取值范围是(-∞，-2)∪[，1]．

3．(典型例题)记函数f(x)=lg(2x-3)的定义域为集合M，函数g(x)=?(1) 集合M，N；

(2) 集合M∩N．M∪N.

[考场错解] (1)由2x-3＞0解得x＞．∴M={x|x＞}．由1-?．

32

32

2

≥0 得x-1≤x-3∴-1≤-3．∴N= x?1

12

12

12

2

的定义域为集合N．求 ?1

2

(2)∴M∩N=?．M∪N={x|x>}． [专家把脉] 求集合N时解不等式1-质，应先移项化为然是错误的．

[对症下药] (1)由2x-3＞0，得x＞．∴M={x|x＞}．由1- ∴x≥3或x<1．∴N={x|x≥3或x<1}．

(2)∴M∩N={x|x>}∩{x|x≥3或x>1}={x|x≥3}．M∪N={x|x>}∪{x|x≥3或x>1}={x|x>或x<1}． 4．(典型例题)若集合M={y|y=2}，P={y|y=x?1}，则M∩P等于 ( ) A．{y|y＞1} B．{y|y≥1} C.{y|y>0} D．{y|y≥0} [考场错解] 选A或B

[专家把脉] 错误地认为是求函数y=2和y=x?1的定义域的交集．实际上是求两函数的值域的交集．

-x

[对症下药] ∵集合中的代表元素为y，∴两集合表示两函数的值域，又∴M={y|y=2}={y|y>0}，P={y|y=x?1}={y|y≥0}．∴M∩P={y|y＞0}，故选C．

专家会诊

1. 对于含有字母的函数求定义域或已知其定义域求字母参数的取值范围，必须对字母酌取值情况进

行讨论，特别注意定义域不能

为空集。2．求函数的值域，不但要重视对应法则的作用，而且要特别注意定义域对值域的制约作用．

考场思维训练

x

1 若函数y=lg(4-a·2)的定义域为R，则实数a的取值范围是 ( )

A．(0，+∞) B．(0，2) C．(-∞，2) D．(-∞，0) 答案：D 解析：∵4-a?2x?0的解集为R?a?

42

在R上恒成立.x

42x

?0,?a?0.

-x

-x

3

2

2

≥0两边同乘以(x-1)不等号不改变方向，不符合不等式性x?1

f(x)

≥0的形式再转化为有理不等式，求解，另外定义域不可能为非空集合．∴N=?显g(x)

3232

?(x?3)(x?1)?02x?3

≥0得 ?0??x?1x?1x?1?

3

2

3232

2 已知函数f(x)的值域是[-2，3]，则函数f(x-2)的值域为 ( ) A．[-4，1] B．[0,5]

C．[-4，1]∪[0，5] D．[-2，3]

答案：D 解析：f(x-2)的图象是把f(x)的图象向右平移2个单位.因此f(x-2)的值域不变.

2

3 已知函数f(x)=lg(x-2mx+m+2)

(1)若该函数的定义域为R，试求实数m的取值范围．

3

答案：解析：(1)由题设，得不等式x-2mx+m+2>0对一切实数x恒成立，

2∴△=（-2m）-4(m+2)<0,解得-1<m<2.

(2)若该函数的值域为R，试求实数m的取值范围．

2答案：由题设，得不等式△=（-2m）-4(m+2) ≥0解得m≤1或m≥2.

24 已知函数f(x)=log3mx?8x?n的定义域为R，值域为[0，2]，求实数m，n的值． 2

x2?1

答案：解析：∵f(x)=log3

u=mx2?8x?n

x2?1

22mx2?8x?nx2?1的值域是[0，2]. ∴u=g(x)=mx2?8x?nx2?1的值域为[1，9].由得（u-m）x-8x+(u-n)=0. ∵x?R,当u?m?0时,??(?8)2?4(u?m)(u?n)?0.当u-m=0时上式仍成立，即有u-(m+n)u+(mn-16) ≤0.

∴关于u的方程u-(m+n)u+mn-16=0有两根1和9，由韦达定理得?2?m?n?1?9解得m=n=5.即为所求。

?mn?16?1?9

命题角度2 函数单调性的应用

2x1．(典型例题Ⅱ)已知a≥0，且函数f(x)=(x-2ax)e在[-1，1]上是单调函数，求a的取值范围．

x2xx2 [考场错解] ∵f′(x)=e(x-2ax)+e(2x-2a)=e[x+2(1-a)x-2a] 又∵f(x)在[-1，1]上是单调函数，

f′(x)≥0在[-1，1]上恒成立.即

x2 e[x+2(1-a)x-2a≥0在[-1，1]上恒成立．

x2 ∵e>0，g(x)=x+2(1-a)x-2a≥0在[-1，1]上恒成立．

?2(1?a)?2(1?a)??1?12???? 即?或△=4(1-a)+8a＜0或? 22?g(?1)?0?g(1)?0.??

解得：a∈?．

故f(x)在[-1，1]上不可能为单调函数．

[专家把脉] 上面解答认为f(x)为单调函数,f(x)就只能为单调增函数，其实f(x)还有可能为单调减函数，因此应令f′(x)≥0或f′(x)≤0在[-1，1]上恒成立．

x2xx2[对症下药] f′(x)=e(x-2ax)+e(2x-2a)=e[x+2(1-a)x-2a]

∵f(x)在[-1，1]上是单调函数．

(1)若f(x)在[-1，1]上是单调递增函数．

x2x则f′(x)≥0在[-1，1]上恒成立，即e[x+2(1-a)x-2a]≥0在[-1，1]上恒成立．∵e>0．∴

g(x)=x+2(1-a)x-2a≥0在[-1，1]上恒成立，则有?2?a?1?1?a?1??12或△=4(1-a)+8a＜0或?

?g(1)?0?g(?1)?0

解得，a∈?．

(2)若f(x)在[-1，1]上是单调递减函数，

则f′(x)≤0在[-1，1]上恒成立．

x2 ∴e[x+2(1-a)x-2a]≤0在[-1，1]上恒成立．

x2 ∵e>0．∴h(x)=x+2(1-a)x-2a≤0在[-1，1]上恒成立． 则有??h(?1)?0??1?03???a?. 4?h(1)?0?3?4a?0

3

4∴当a∈[，+∞]时，f(x)在[-1，1]上是单调函数．

4

2．(典型例题)已知函数f(x)=a+xx?2(a＞1) x?1

(1)证明：函数f(x)在(-1，+∞)上为增函数；

(2)用反证法证明方程f(x)=0没有负数根．

[考场错解] (1)设-1＜x1＜x2，f(x2)-f(x1)=a+

∴f(x)在(-1，+∞)上是增函数．

(2)设x0为方程f(x)=0的负数根，则有a+

∵x0≠-1，∴当-1<x0<0时，0<x0+1<1.

∴原方程没有负数根．

[专家把脉] 第(1)问错在用定义证明函数单调性时，没有真正地证明f(x2)>f(x1)．而只是象征性地令f(x2)-f(x1)＞0这是许多学生解这类题的一个通病．第(2)问错在把第(1)问的条件当成第(2)问的条件，因而除了上述证明外，还需证明x0<-1时，方程也没有负根．

[对症下药]

(1) 设-1<x1<x2,f(x2)-f(x1)=a+

a-a+x2x1x2x0x2x2?2x?2x?2x1?2x2x1＞0． ?ax1?1?a-a+2?x2?1x1?1x2?1x1?1x0?23x02?x0=0．即a==-1+， ① x0?1x0?1x0?1133x0>3，-1+>2，而＜a<1 与①矛盾． a1?x01?x0x2?2x?2= ?ax1?1x2?1x1?1x2?2x1?2x1x2-x13(x2?x1)(x?1)(x2?2)?(x1?2)(x2?1)x1x2-x1=a(a-1)+1=a(a)+. ?x2?1x1?1(x2?1)(x1?1)(x2?1)(x1?1)

∵x2-x1>0，又a>1，

x2-x1∴a>1．而-1<x1<x2.∴x1+1>0，x2+1>0．

∴f(x2)-f(x1)＞0

∴f(x)在(-1，+∞)上为增函数．

(2)设x0为方程f(x)=0的负数根，则有a+

显然x0≠-1，

当0＞x0＞-1时，1＞x0+1＞0的解．

当x0<-1时．x0+1＜033x0<0，-1+＜-1，而a>0矛盾．即不存在x0<-1的解． 1?x01?x0

3x0x0?23?(1?x0)3x02?x0=0．即a=. ??-1+x0?1x0?1x0?1x0?1133xO＞3，-1+>2．而<a<1．这是不可能的，即不存在0＞x0>-1a1?x01?x03．(典型例题)若函数f(x)=l0ga(x-ax)(a＞0且a≠1)在区间(-，0)内单调递增，则a的取值范围

是 ( ) A.[，1] B.[，1] C.[，+∞] D.(1，-) 9

494143412

5

[考场错解] A 当a∈(0，1)时，要使f(x)=loga(x-ax)在区间(-，0)上单调递增．∴x-ax＞0在(-，0)上恒成立，∴(-)+a≥0 a≥.综合得a∈[，1].当a>1时，x-ax>0在(-,0)上不可能成立．

[专家把脉] 上面解答根本没有按复合函数单调性法则进行判断，而只是考虑函数的定义域，这样的答案肯定是错误的．

3

[对症下药] 设?(x)=x-ax

当0＜a＜1时，依题意,(x)在(-，0)上单调递减且?(x)在(-，0)上大于0． ∵?′(x)=3x-a.即?′(x)≤0在(-，0)上恒成立?a≥3x在(-，0)上恒成立． ∵x∈(-，0)∴3x∈(0，). ∴a≥．此时?(x)>0．∴≤a<1． 当a>1时，?(x)在(-，0)上单调递增， ∴?′(x)=3x-a≥0在(-，0)上恒成立． ∴a≤3x在(-，0)上恒成立． 又3x∈(0，)·∴a≤0与a＞1矛盾． ∴a的取值范围是[，1].

故选B. 专家会诊

1.讨论函数单调性必须在定义域内进行，因此讨论函数的单调性必须求函数定义域．

2．函数的单调性是对区间而言的，如果f(x)在区间(a，b)与(c，d)上都是增(减)函数，不能说 f(x)在(a，b)∪(c，d)上一定是增(减)函数．

3．设函数y=f(u)，u=g(x)都是单调函数，那么复合函数y=f[g(x)]在其定义域上也是单调函数．若y=f(u)与u=g(x)的单调性相同，则复合函数y=f[g(x)]是增函数；若y=f(u)，u=g(x)的单调性相反，则复

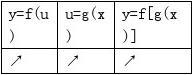
34

2

2

22

3

12

3

1212

3

121414

3

12

1212

12

2

12

12

2

34

3434

12

12

12

34

6

．

考场思维训练

1 函数f(x)对任意实数x都有f(x)<f(x+1)那么 ( )

A.f(x)是增函数

B.f(x)没有单调减区间

C.f(x)可能存在单调增区间，也可能不存在单调减区间

D．f(x)没有单调增区间

C 解析：根据函数单调性定义进行判断.

2 函数y=log1(x-3x+2)的单调增区间是_______.单调递减区间是_________.

22

解析：(-∞,1),(2,+ ∞)根据复合函数单调性法则进行求解。

3 如果函数f(x)的定义域为R，对于任意实数a，b满足f(a+b)=f(a)·f(b)．

*(1)设f(1)=k(k≠0)，试求f(n)(n∈N)

答案：解

(1)

?f(n?1)?f(n)?f(1),?析f(n?1)?f(1)?k?0.??f(n)?是以k为首项,k为公比的等比数例,?f(n)?f(1)?[f(1)]n?1?kn.(n???)f(n)

(2) 设当x＜0时,f(x)＞1，试解不等式f(x+5)＞

答案：(2)对任意的 1. f(x)

xxxx?R,f(x)?f(?)?f2()?0,假定存在xo?R,使f(xo)?0,则取x?0,有f(x)?f(x?xo?xo)?f(x?xo)?f(xo)?0.这与已知相矛盾则f(222

?0,于是对任意x?R,必有f(x)?0.

2∵f(0)=f(0+0)=f(0)≠0.

∴f(0)=1, 设x1<x2, 则x1-x2<0则f(x1-x2)>1,又∵f(x2)>0.

∴f(x1)=f[(x1-x2)+x2]=f(x1-x2) ?f(x2)>f(x2). ∴f(x)为R上的减函数，解不等式f(x+5)>1 f(x)

∵f(x)>0, ∴不等式等价于f(x+5) ?f(x)>1.即f(2x+5)>f(0),又∵f(x)为减函数，∴2x+5<0.

5?解得不等式的解集为??x|x??? ?2?

4 是否存在实数a，使函数f(x)=loga(ax-x)在区间[2，4]上是减函数?

１．答案：解析：设?(x)=ax-x=a(x?22121)?当a>1时，要使f(x)在区间[2，4]上是减函数，则有： 2a4a

7

?a??1??4?????2a

??(4)?0?a????1

8

?a?? 14

?

?1a??当0<a<1时，要使f(x)在[2，4]上是减函数，则有??2?

???2a

??(2)?0?a????1

412

?a?

1 .2

即

1

?a?1. 2

12

综合，得存在实数a，且a的范围为(,1).

命题角度3 函数的奇偶性和周期性的应用 1．(典型例题)定义在R上的偶函数f(x)满足f(x)=f(x+2)，当x∈[3，4]时,f(x)=x-2．则 ( ) A．f(sin)＜f(cos) B．f(sin

1

2

12

??)＞f(cos) 33

3

2

C．f(sin1)＜f(cos1) D.f(sin)＜f(cos)

[考场错解] A 由f(x)=f(x+2)知T=2为f(x)的一个周期．设x∈[-1，0]知x+4∈[3，4] ∴f(x)=f(x+4)=x+4-2=x+2． ∴f(x)在[-1，0]上是增函数 又f(x)为偶函数．∴f(x)=f(-x)

∴x∈[0，1]时,f(x)=x+2，即f(x)在[0，1]上也是增函数．又∵sin＜cos

1

2

111

? f(sin)＜f(cos)．

222

3

2

[专家把脉] 上面解答错在由f(x)=f(-x)得f(x)=x+2这一步上，导致错误的原因主要是对偶函数图像不熟悉．

[对症下药] C 由f(x)=f(x+2)知T=2为f(x)的一个周期，设x∈[-1，0]，知x+4∈[3，4] ∴f(x)=f(x+4)=x+4-2=x+2． ∴f(x)在[-1，0]上是增函数．

又∵f(x)为偶函数，∴f(x)的图像关于y轴对称． ∴f(x)在[0，1]上是减函数． A：sin<cos B：sin

12

111?f(sin)>f(cos) 222

???2

＞cos?f(sin)＞f(cos)． 3333

C：sin1>cos1?f(sin1)<f(cos1)．

故正确答案C．

2．(典型例题)若函数f(x)是定义在R上的偶函数，在(-∞，0)上是减函数，且f(2)=0，则使得f(x)＜0的x的取值范围是 ( )

8

A．(-∞，2)

B．(2，+∞)

C．(-∞，-2)∪(2，+∞)

D．(-2，2)

[考场错解] C f(-x)=f(x)＜0=f(2)．∴x＞2或x<-2．

[专家把脉] 以上解答没有注意到偶函数在对称区间的单调性相反．错误地认为f(x)在[0，+∞]上仍是减函数，导致答案选错．

[对症下药] D ∵f(x)是偶函数，∴f(-x)=f(x)=f(|x|)．∴f(x)<0．f(|x|)＜f(2)．又∵f(x)在(-∞，0)上是减函数，∴f(x)在[0，+∞]上是增函数，|x|＜2?-2<x<2．选D．

3．(典型例题)设f(x)是定义在R上的奇函数，且y=f(x)的图像关于直线x=

f(1)+f(2)+f(3)+f(4)+f(5)=_______

[考场错解] 填-f(0) ∵f(x)是定义在R上的奇函数，∴f(-x)=-f(x)．又f(x)的图像关于x=对称．

∴f(x)=f(1-x) ∴f(-x)+f(-x+1)=0．

∴f(x)+f(x-1)=0

∴f(5)+f(4)=0．f(3)+f(2)=0．f(1)+f(0)=0．

∴f(5)+f(4)+f(3)+f(2)+f(1)=-f(0)

[专家把脉] 上面解答忽视了奇函数性质的运用．即f(x)在x=0处有定义?f(0)=0．

[对症下药] 填0 依题意f(-x)=-f(x)．f(x)=f(1-x)．∴f(-x)=-f(1-x) 即f(-x)+f(1-x)= 0 f(x)+f(x-1)=0 ∴f(5)+f(4)=0，f(3)+f(2)=0．f(1)+f(0)=0．又∵f(x)在x=0处有定义，∴f(0)=0∴f(5)+f(4)+f(3)+f(2)+f(1)=f(1)=-f(0)=O.

4．(典型例题)设函数f(x)在(-∞，+∞)上满足f(2-x)=f(2+x)．f(7-x)=f(7+x)，且在闭区间[0，7]上，只有f(1)=f(3)=0．

(1)试判断函数y=f(x)的奇偶性；

(2)试求方程f(x)=0在闭区间[-2005，2005]上根的个数，并证明你的结论．

[考场错解] 依题意f(x)=f(4-x)．f(x)=f(14-x)．∴f(4-x)=f(14-x)，∴f(x)=f(x+10)∴f(x)是以 10为周期的函数,f(3)=0．∴f(-3)=f(7)=0．

∴f(3)=f(-3)=-f(3)．∴f(x)既是奇函数又是偶函数．

(2)由(1)知f(x)是周期为10的周期函数，又f(3)=f(1)=0，∴f(11)=f(13)=f(-)=f(-9)=0．

故f(x)在[0，10]上有两个解，从而可知函数y=f(x)在[0，2005]上有401个解．[-2005，0]上有401个解，所以函数丁y=f(x)在[-2005，2005]上有802个解．

[专家把脉] (1)对题意理解错误，题设中“在闭区间[0，7]上，只有f(1)=f(3)=0”说明除了f(1)、f(3)等于 0外再不可能有f(7)=0．(2)因f(x)在R上既不是奇函数，又不是偶函数．不能认为x∈[0，10]，

[-10，0]上各有两个解，则认为在[0，2005]与在[-2005，0]上解的个数相同是错误的，并且f(x)=0在[0，2005]上解的个数不是401个，而是402个．

[对症下药] 由f(2-x)=f(2+x)，f(7-x)=f(7+x)得函数丁y=f(x)的对称轴为x=2和x=7．

从而知函数y=f(x)不是奇函数． 121对称，则2

9

由??f(2?x)?f(2?x)?f(x)?f(4?x)从而知f(x)是周期为10的???f(4-x)=f(14-x)?f(x)=f(x+10)．f(7?x)?f(7?x)f(x)?f(14?x)??

周期函数．

又f(3)=f(1)=0,而f(7)=f(-3)≠0．

故函数y=f(x)是非奇非偶函数．

(2)由(1)知f(x)是以周期为10的周期函数．

∴f(1)=f(11)=?=f(2001)=0

f(3)=f(13)=?=f(2003)=0

f(x)=0在[0，2005]上共有402个解．同理可求得f(x)=0在[-2005，0]上共有400个解．

∴f(x)=0在[-2005，2005]上有802个解．

专家会诊

1．函数奇偶性定义是判断函数奇偶性的主要依据，为了便于判断有时需要将函数进行化简．

2．要注意从数和形两个角度理解函数的奇偶性，要充分利用f(x)与f(-x)之间的转化关系和图像的对称性解决有关问题．

3．解题中要注意以下性质的灵活运用.

(1)f(x)为偶函数?f(x)=f(-x)=f(|x|)．

(2)若奇函数f(x)的定义域包含0，则f(0)=0.

考场思维训练

1 f(x)是定义在R上的偶函数，且g(x)是奇函数，已知g(x)=f(x-1)，若g(-1)=2006，则f(2006)的值为 ( )

A．2005 B．-2005

C.-2006 D．2006

答案：D 解析：由题设条件易得f(x+4)=f(x), ∴f(2006)=f(2).又f(-2)=g(-1)=2006. ∴f(2006)=2006.

?x?2,x??1,

2 函数f(x)=lg(1+x)，g(x)=?h(x)=tan2x中________是偶函数． ?0,|x|?1,

??x?2,x?1,?2

答案：解析：f(x)、g(x).运用奇偶性定义进行判断。

23 设f(x)是定义在R上的奇函数，且对任意实数x恒满足f(x+2)=-f(x)．当x∈[0，2]时，f(x)=2x+x．

(1)求证:f(x)是周期函数；

答案：解析：(1)f(x+2)=-f(-x), ∵f(x+4)=-f(x+2)=f(x)

∴f(x)是周期为4的周期函数。

(2)当x∈[2，4]时，求f(x)的解析式；

22答案：当x∈[-2,0]时，-x∈[0,2],由已知得f(-x)=2(-x)-(-x)=-2x-x.

22又f(x)是奇函数，∴f(-x)=-f(x)=-2x-x. ∴f(x)=x+2x.

2又当x ∈[2,4]时，x-4∈[-2,0], ∴f(x-4)=(x-4)+2(x-4).

又f(x)是周期为4的周期函数。

22∴f(x)=f(x-4)=(x-4)+2(x-4)=x-6x+8.

2因而求得 x∈[2,4] 时f(x)=x-6x+8.

(3) 计算:(0+)f(1)+f(2)+?+f(2004)

答案：f(0)=0f(2)=0f(1)=1f(3)=-1,又f(x)是周期为4的周期函数。

∴f(0)+f(1)+f(2)+f(3)=f(4)+f(5)+f(6)+f(7)=?=f(2000)+f(2001)+f(2002)+f(2003)=0.

10

又f(2004)=f(0)=0, ∴f(0)+f(1)+f(2)+ ?+f(2004)=0.

4 设a、b∈R，且a≠2定义在区间(-b，b)内的函数f(x)=lg

答案：解析：f(x)=lg1?ax是奇函数，求b的取值范围． 1?2x1?ax(?b?x?b)是奇函数，等价于，对任意x∈(-b,b)都有：1?2x

?f(?x)??f(x)? ① ?1?2ax?0?1?2x?

②

① 式即为lg

(2)得

1

21?ax1?2x2222?lg.即ax=4x.此式对任意x∈(-b,b)都成立相当于a=4, ∵a≠2, ∴a=-2.代入1?2x1?ax1?2x1?2x?0 12121212即??x?.此式对任意x?(?b,b)都成立相当于???b?b?所以得b的取值范围为(0,].

命题角度4 反函数的概念和性质的应用

21．(典型例题)函数f(x)=x-2ax-3在区间[1，2]上存在反函数的充分必要条件是 ( )

A．a∈(-∞，1)

B．a∈[2，+∞]

C．a∈[1，2]

D．a∈(-∞，1)∪[2，+∞]

[考场错解] 选A或B ∵a∈(-∞，1]∴f(x)在区间[1，2]上是增函数．∴f(x)存在反函数．当a∈

[2，+∞)．对称轴x=a在区间[1，2]的右侧，∴f(x)在 [1，2]上是减函数．∴f(x)存在反函数．

[专家把脉] 上面解答只能说明A或B是f(x)存在反函数的充分条件，并不是充要条件．

[对症下药] ∵一个函数在某区间上存在反函数的充要条件是此函数在这个区间上是单调函数．

∴对称轴x=a不应在(1，2)内，∴a≤1或a≥2．故选C.

2．(典型例题Ⅰ)y=2x?x2(1≤x≤2)的反函数是 ( ) A.y=1+?x2(-1≤x≤1) B.y=1+?x2 (0≤x≤1) C.y=1-?x2 (-1≤x≤1) D.y=1-?x2 (0≤x≤1)

[考场错解] C ∵y=2x-x．∴(x-1)=1-y．∴x-1=-?y2，∴x=1-?y2．x、y对换得y=1-?x2 又1-x≥0．∴-1≤x≤1．因而f(x)的反函数为y=1-?x2(-1≤x≤1)． 22222

11

[专家把脉] 上面解答有两处错误(一)∵1≤x≤2,∴x-1≥0．由(x-1)=1-y开方取“正号”而不是取“负号”；(二)反函数的定义域应通过求原函数的值域而得到，而不是由反函数解析式确定．

[对症下药] B 由y=2x?x2?(x-1)=1-y．∴x∈[1，2]x-1∈[0，+∞]．∴2222

x-1=?y2?=1+?y2．x、y对换得y=1+?x2 又∵y=2x?x2??(x?1)2?1(1≤x≤2)．∴0≤y≤1即原函数值域为[0，1]．所以反函数为y=1-?x2 (0≤x≤1).选B.

3．(典型例题)设f(x)是函数f(x)=(a-a)(a＞1)的反函数，则使f(x)＞1成立的x的取值范围为 ( )

a2?1a2?1 A．(，+∞) B．(-∞，) 2a2a

a2?1 C．(,a) D．(a，+∞) 2a

2y?2y2?11x-x2xxx [考场错解] C ∵y= (a-a)，∴a-2y·a-1=0．a==y+22

-1-1-112x-x-1y2?1．∴x=loga(y+y2?1)，x、y对换．∴f(x)=loga(x+x2?1)(x∈R)又∵f(x)＞1，∴loga(x+x2?1)＞1?x ?x?aa2?12+x2?1＞a. x2?1＞a-x??∴<x<a．选C. ?a?12ax??2a?

[专家把脉] 上面解答错在最后解不等式x2?1＞a-x，这一步，因为x+x2?1＞a-x应等价于?a?x?0??a2?1或a≤x.错解中只有前面—个不等式组．答案显然错了.

?x?2a?

2y?2y2?11x-x2xxx [对症下药] A 解法1 ∵y=(a-a)?a-2y·a-1=0，a==y+22y2?1∴

x=loga(y+y2?1)．∴f(x)=loga(x+x2?1)(x∈R)．∵f(x)>1

?a?x?0 ∴loga(x+32?1)>1?x+x2?1>a?x2?1＞a-x???2a2?1＜x＜+∞. 2a-1-1??x?1?(a?x)或a?x?0?2

解法2：利用原函数与反函数的定丈域、值域的关系．原题等价于x>1时，f(x)=(a-a)的值域，∴f(x)=(a-a)在R上单调递增．∴f(x)＞(a-1

2x-x12x-x121a2?1)=．选A. a2a

-1-14.(典型例题)设函数f(x)的图像关于点(1，2)对称，且存在反函数f(x)，f(4)=0，f(4)=________．

-1 [考场错解] 填0 ∵y=f(x)的图像关于点(1，2)对称，又∵f(4)=0，∴f(0)=4，∴f(4)=0

[专家把脉] 上面解答错在由图像过点(4，0)得到图像过点(4，0)上，因为f(x)图像关于点(1，2) 12

对称不是关于y=x对称，因此应找出图像过点(-2，4)是关键．

[对症下药] 填-2．

解法1 ∵f(4)=0，∴f(x)的图像过点(4，0)．又∵f(x)的图像关于点(1，2)对称，∴f(x)的图像过

-1点 (2-4，4-0)即(-2，4)．∴f(-2)=4．∴f(4)=-2．

解法2 设y=f(x)上任一点P(x、y)关于点(1，2)对称的点为P′(2-x，4-y)．依题意4-y=f(2-x)，

-1∴4-f(x)=f(2-x)? f(x)+f(2-x)=4．令x=4．∴f(4) +f(-2)=4.又f(4)=0，∴f(-2)=4．∴f(4)=-2．

专家会诊

-1 1.求反函数时必须注意：(1)由原解析式解出x=f(y)，如求出的x不唯一，要根据条件中x的范围决

定取舍，只能取一个；(2)要求反函数的定义域，即原函数的值域．

2．分段函数的反函数可以分别求出各段函数的反函数后再合成．

-1 3．若点(a，b)在原函数y=f(x)的图像上，则(b，a)在反函数y=f(x)的图像上．

考场思维训练

21 函数y=3x-1(-1≤x＜0)的反函数是 ( )

A．y=?log3x(x≥)

B．y=-?log3x (x≥)

C．y=?log3x (<x≤1) D.y=-?log3x (<x≤1)

答案：D 解析：由y=3x2-113131313得 x-1=log3y ∵-1≤x<0, ∴x=-log3x?1,xy互换得y??log3x?1,

11?3x2?1?1.故原函数的反函数为:y???log3x(?x?1)选D. 332??1?x?0,??1?x2?1?0,?

2 (典型例题)定义在R上的函数y=f(x)为周期函数，最小正周期为T，若函数y=f(x)，x∈(0,T)时E

-1有反函数y=f,x∈D．则函数y=f(x)，x∈(2T,3T)的反函数为 ( )

-1 A.y=f(x)，x∈D

-1 B．y=f(x-2T),x∈D

-1 C.y=f(x+2T)，x∈D

-1 D.y=f(x)+2T．x∈D

答案：D 解析：∵x∈(2T,3T), ∴x-2T=(0,T).又∵f(x)的周期为2T，y=f(x)=f(x-2T). ∴

-1x-2T=f(y)+2T,x,y互换，得

-1-1y=f(x)+2T.当x∈(2T,3T)的反函数为y=f(x)+2T,x∈D.

3 已知f(x)=a?x-1的反函数．f(x)的图像的对称中心是(-1，3)，求实数a的值． x?a?1

答案：解析：∵f(x)=-1-1-1的对称中心是（a+1,-1）∴f(x)的对称中心是（-1,a+1）, ∴a+1=3,x?(a?1)

从而a=2.

探究开放题预测

预测角度1 借助函数单调性求函数最值或证明不等式

13

1．已知定义域为[0，1)的函数f(x)同时满足①对任意x∈[0，1]，总有f(x)≥0；②f(1)=1；③若x1≥0，x2≥0，x1+x2≤1，则有f(x1+x2)≥f(x1)+f(x2)．

(1)求f(0)的值；

(2)求函数f(x)的最大值．

[解题思路] (1)令x1=x2=0可得答案(2)，先证f(x)在[0，1]上是单调函数，再求其最大值．

[解答] (1)令x1=x2=0，由条件①得f(0)≥0，由条件③得f(0)≤0．故f(0)=0．

(2)任取0≤x1≤x2≤1，可知x2-x1∈(0，1)，则f(x2)=f[(x2-x1)+x1]≥f(x2-x1)+f(x)．又∵x1- x2∈(0，

1)，∴f(x2-x1)≥0．∴f(x)≥f(x1) ∴f(x)在[0，1]上是增函数，于是当0≤x≤1时，有f(x)≤f(1)=1．∴当x=1时，[f(x)]max=1．即f(x)的最大值为1．

2．设f(x)是定义在(0，+∞)上的函数，k是正常数，且对任意的x∈(0，+∞)，恒有f[f(x)]=kx成立．

(1) 若f(x)是(0，+∞)上的增函数，且k=1，求证：f(x)=x．

(2)对于任意的x1、x2∈(0，+∞)，当x2>x1时，有f(x2)-f(x1)＞x2-x1成立，如果k=2，证明：＜＜．

[解题思路] (1)用反证法证明；(2)用反证法先证f(x)＞x，再运用函数单调性进行放缩．

[解答] (1)假设f(x)＞x

∵f(x)在(0，+∞)上是增函数，且f(f(x)]=x.

∴f(x)＞f[f(x)]．

∴x＞f(x)这与假设矛盾．∴f(x)＞x不可能成立

同理可证f(x)＜x也是不可能成立的．

综合，得f(x)=x.

(2)先证f(x)＞x，假设存在x0∈(0，+∞)，使得f(x0)≤x0，若f(x0)=x0，则f[f(x0)]=f(x0)．即2x0= f(x0)=x0，∴x0矛盾；若f(x0)＜x0，由条件可知f(x)在(0，+∞)上是增函数，且f(x0)＞0．

∴f[f(x0)]<f(x0)，即2x0<f(x0)．

∴2x0<x0?x0<0矛盾，∴f(x)>x

因此,f{f[f(x)]}-f[f(x)]＞f[f(x)]-f(x)＞f(x)-x．

即2f(x)-2x>2x-f(x)>f(x)-x 解得＜43f(x)3＜． x23243f(x)x

预测角度2 综合运用函数奇偶性、周期性、单调性进行命题

1．设f(x)是定义在[-1，1]上的偶函数．当x∈[-1，0]时，f(x)=g(2-x)，且当x∈[2,3]时，

3g(x)=2a(x-2)-4(x-2)，

(1)求f(x)的表达式；

(2)是否存在正实数a(a＞6)，使函数f(x)的图像的最高点在直线y=12上，若存在，求出正实数a的值；若不存在，请说明理由．

[解题思路] (1)运用函数奇偶性和条件f(x)=g(2-x)可求得f(x)的解析式．(2)利用导数可求得f(x)的最大值．令最大值等于12可知是否存在正实数a．

[解答] (1)当x∈[-1，0]时，2-x∈[2，3]

33f(x)=g(2-x)=2a(-x)-4(-x)=4x-2ax

14

得f(x)=4x-2ax(x∈[-1，0])

∵y=f(x)在[-1，1]上是偶函数

3∴当x∈[0，1]时，f(x)=f(-x)=-4x+2ax

3??4x?2ax∴f(x)=?3???4x?2ax3?1?x?0,0?x?1.

(2)命题条件等价于[f(x)]max=12，因为f(x)为偶函数，所以只需考虑0≤x≤1的情况．

2 求导f′(x)=-12x+2a(0≤x≤1，a>6)，

由f′(x)=0得x=

∵aa或x=-(舍)． 66a＞1，当0≤x≤1时 f′(x)>0，f(x)在[0，1]上单调递增， 6

∴[f(x)]max=f(1)=12，∴a=8．

综上，存在a=8使得f(x)的图像的最高点在直线y=12上．

2．函数y=f(x)是偶函数，且是周期为2的周期函数，当x∈[2，3]时,f(x)=x-1．在y=f(x)的图像上有两点A、B，它们的纵坐标相等，横坐标都在区间[1，3]上，定点C的坐标为(0，a)，(其中a＞2)，求△ABC面积的最大值．

[解题思路] 先利用函数的周期性和奇偶性分别求出f(x)在[0，1]和[1，2]时的解析式，再利用图象设出 A、b的坐标，然后以A、B的纵坐标作为自变量建立面积函数关系，借助函数关系式即可求得S△ABC的最大值．

[解答] ∵f(x)是以2为周期的周期函数，当x∈[2，3]时,f(x)=x-1．

∴当x∈[0，1]时，f(x)=f(x+2)=(x+2)-1=x+1．

又∵f(x)是偶函数，∴当x∈[-1，0]时，f(x)=f(-x)=(-x)+1=-x+1；当x∈[1，2]时．f(x)=f(x-2)=-(x-2)+1=-x+3．

设A、B的纵坐标为t(1≤t≤2)，并设A在B的左边，则A、B的横坐标分别为3-t、t+1，则|AB|=(t+1)-(3

a?12(a?1)212-t)=2t-2，∴△ABC的面积S=(2t-2)(a-t)=-t+(a+1)t-a=-(t-)+-a． 224

3a?1a2?2a?1 ∴当<≤2即2<a≤3时，S有最大值． 224

当a?1>2，即a>3时，函数S在[1，2]上单调递增，∴S有最大值S(2)=a-2． 2

预测角度3 反函数与函数性质的综合

1．在R上的递减函数f(x)满足：当且仅当x∈M?R+函数值f(x)的集合为[0，2]且f()=1；又对M中的任意x1、x2都有f(x1·x2)=f(x1)+f(x2)．

(1)求证：∈M，而1

41?M； 8

-1-1-1-112 (2)证明:f(x)在M上的反函数f(x)满足f(x1)·f(x2)=f(x1+x2)．

(3)解不等式f(x2+x)·f(x+2)≤(x∈[0，2])．

[解题思路] 由给定的函数性质，证明自变量x是属于还是不属于集合"，最后利用反函数的概念、-1-114 15

性质证明反函数的一个性质和解反函数的不等式．

[解答] (1)证明：∵∈M，又=×,f()=1．∴f()=f(×)=f()+f()=1+1=2∈[0，2]， ∴∈M，

又∵f()=f(×)=f()+f()=1+2=3?[0，2]．∴?M.

(2)证明：∵f(x)在M上递减，∴f(x)在M上有反函数f(x)，x∈[0，2]．

-1-1

任取x1、x2∈[0，2]，设y1=f(x1)，y2=f(x2)． ∴x1=f(y1)，x2=f(y2)(y1，y2∈M)

-1

∵x1+x2=f(y1)+f(y2)=f(y1·y2)，∴y1·y2=f(x1+x2)

-1-1-1-1-1

又y1·y2=f(x1)·f(x2)，∴f(x1)·f(x2)=f(x1+x2)．

-1

(3)∵f(x)在M上递减，∴f(x)在[0，2]上也递减， ∴f(x2+x)·f(x+2)≤等价于f(x+x+x+2)≤f(2)．

?0?x2?x?2,??2?x??1或0?x?1???

?x?0. ∴?0?x?2?2,???2?x?0

?2?x??2或0?x?2??x?2x?2?2.?

-1

-1

-1

1

21412xxxxxxxxxxxx2

14

181214121418

14

-12-1

故不等式的解集为{x|x=0}.

x

2．已知奇函数f(x)，偶函数g(x)满足f(x)+g(x)=a(a＞0且a≠1). (1) 求证:f(2x)=2f(x)·g(x)

(2) 设f(x)的反函数为f(x)，当a=a-1时，试比较f[g(x)]与-1的大小，并证明你的结论． (3) 若a>1，n∈N且n≥2，比较f(n)与nf(1)的大小，并证明你的结论.

x

[解题思路] 先根据函数f(x)·g(x)的奇偶性和f(x)+g(x)=a可解出f(x)·g(x)．再借助基本不等式和叠加法证明后两小题.

x

[解答] (1)f(x)+g(x)=a，

-xx

又f(-x)+g(-x)=a，而f(x)是奇函数，g(x)是偶函数，∴-f(x)+g(x)=a,

∴f(x)=

ax?a?xax?a?x

,g(x)=． 22

*

-1

-1

ax?a?xax?a?xa2x?a?2x1

∴f(x)·g(x)= ·==f(2x)

2224

(2)∵0<a=2-1<1． ∴f(x)=

f(-1)=

ax?a?x

是(-∞，+∞)上的减函数，则其反函数也是减函数，又由于 2

(?1)?1?(2?1)

=1．

2

2ax?a?x

∵g(x)=≥=1=f(-1)

22

16

∴f[g(x)]≤-1．

(3)f(n)-nf(1)= 12-1 (a-a)- n-n12n(a-a)=-11

2 (a-a)[a+a+-1n-1n-3?+a-(n-3) +a-(n-1)]-

-1-1n-1n-3-(n-3)-(n-1)11n(a-a)=(a-a)[a+a+?+a+a-n] 22

当a>1时，a-a>0

n-1-(n-1)a+a＞2

n-3-n(n-3)a+a＞2

??

n-1n-3-(n-1)-(n-3)∴a+a+?+a+a＞0

∴f(n)-nf(1)＞0,即f(n) ＞nf(1)

考点高分解题综合训练

1 函数f(x)=x+x2?1,则其反函数的定义域是 ( )

A．(-∞，-1)∪[1，+∞)

B．[1，+∞)

C．[-1，0]

D．[-1，0]∪(1，+∞)

2答案：D 解析：反函数的定义域即为原函数的值域，x-1≥0?x≥1或x≤-1,当x≥1时，函数f(x)是单

调递增函数，此时值域为（1，+∞）当x≤-1时，f(x)=x+x2?1?1

x?x?12-1为单调递减函数，此时值域

为[-1，0]，故值域为[-1，0]∪(1,+ ∞), 从而选D.

2 已知定义域为R的函数f(x)满足f(-x)=-f(x+4)．当x＞2时，f(x)单调递增，如果x1+x2<4且(x1-2)(x2-2)<0，则f(x1)+f(x2)的值为 ( )

A.可能为0 B．恒大于0

C.恒小于0 D．可正可负

答案：C 解析：不妨设x1<x2,则x1<2<x2,且x1+x2<4,由f(-x)=-f(x+4)可知，函数f(x) 的图象关于点（2，0）成中心对称，函数在（2，+∞）上单调递增，∴f(x1)+f(x2)<f(x1)+f(4-x1)=f(x1)-f(x1)=0,故选C.

3 已知函数f(x)是定义在R上的奇函数，当x<0时，f(x)=()，那么f(x)=()，那么f(0)+f(-8)的值为 ( )

A．2 B．-3 C．3 D．-2

?1x(x?0)?(2)

?,故f?1(0)?0 答案：C解析：f(x)=?0(x?0)

?x??2(x?0)??12x12x-1-1

f(-8)=3.故选 C.

4. B 解析：①?x?的值域为[0，1]；②③正确；④错误

4 符号[x]表示不超过x的最大整数，如[π]=3，[-1．08]=-2，定义函数{x}=x-[x]，那么下列命题-1 17

中正确的个数是 ( )

①函数{x}的定义域为R，值域为[0，1]；

②方程{x}=有无数解；

③函数{x}是周期函数；

④函数{x}是增函数．

A.1个 B．2个 C．3个 D．4个

答案：C解析：∵f(x)的周期为3，∴f(2)=f(-1)=-f(1)<-1.即2a?32??1.解得?1<a<.故选C. a?13

2a?3，则 ( ) a?15 设函数f(x)是定义在R上的以3为周期的奇函数，若f(1)＞1,f(2)=

A．a< B．a＜且a≠-1 C.-1<a< D．m>或m<-1 2

3232323

答案：D 解析：因为函数y=f(x)为偶函数，所以y=f(1-x)=f(x-1),它的图可由y=f(x)的图向右平移1个单位得到，故对称轴为x=1,且在（4，6）内是增函数，故选D。

6 已知定义在R上的偶函数y=f(x)的一个单调递增区间是(3，5)，则函数y=f(1-x) ( )

A.图像的对称轴为x=-1，且在(2，4)内是增函数

B．图像的对称轴为x=1，且在(2，4)内是减函数

C.图像的对称轴为x=0，且在(4，6)内是增函数

D．图像的对称轴为x=1，且在(4，6)内是增函数

2答案：解析：[-1，3]由x-2x-8≥0?x≤-2或x≥4.由1-|x-a|>0?|x-a|<1?a-1<x<a+1,又由A∩B=?，

故??a?1??2,?a??1解得?即?1?a?3. a?1?4,a?3,??

7 函数f(x)=x2?2x?8的定义域为A，g(x)=1

?|x?a|的定义域为B，且A∩B=? ，则实数a的取值

范围是_________

2答案：解析：[-1，3]由x-2x-8≥0?x≤-2或x≥4.由1-|x-a|>0?|x-a|<1?a-1<x<a+1,又由A∩B=?，

故??a?1??2,?a??1解得?即?1?a?3. a?1?4,a?3,??

8 已知y=f(x)是函数f(x)=?

g(x)=________

２．答案：解析：?

?x?1,f?1(x)????x,?1?,?1,0?x?1,?1?x?1.-1?x?1,?1?x?0.-1的反函数，则函数g(x)=f(x)+f(x)的表达式是??x,0?x?1. 0?x?1, ?1?x?0.

??1,

?1,0?x?1, ?1?x?1.

2故f(x)?f?1(x)??9 已知函数f(x)在定义域上是减函数，且f(a-1)>f(1-a)．求a的取值范围；

18

??1?a?1?1??答案：解析：由牺件可得??1?a2?1?1,

?2??a?1?1?a.解得0?a?1.

10 若f(x)满足：在(0，+∞)上f(xy)=f(x)+f(y)，且对x＞1，f(x)>0恒成立，求证：f(x)存在反函

a?b-1-11数f(x)并比较f2与 [f(a)+f(b)]的大小． 2-1-1

答案：解析：∵f(x,y)=f(x)+f(x) ∴f(x)=f(?y)?f()?f(y).?f()?f(x)?f(y).

设0<x1<x2,则x2x?1,有f(x2)?f(x1?f(2)?0 xc1x1xyxyxy

∴f(x1)<f(x2)从而f(x)在区间（0，+∞）上单调递增，则有f(x)存在反函数。

-1-1-1-1-1-1-1令f(x)=uf(y)=u,则f(u)=x,f(u)=y. ∴u+v=f[f(u)]+f[f(u)]=f[f(u)?f(u)]

x()2∴f(u+v)=f(u) ?f(v), ∴f(x)=[f2]∴-1-11--1-1

1?11?ab?ababa?b[f(a)?f?1(b)]??f?1()]2?[f?1()]2??f?1()?f?1()?f?1(?)?f?1(). 22?22?22222

故f?1(a?b1)?[f?1(a)?f?1(b)]. 22

11 已知集合A=[2，log2t]，集合B={x|x2-14x+24≤0}，x1t∈R，且A?B．

(1)对于区间[a，b]，定义此区间的“长度”为b-a． 若A的区间“长度”为3，试求t的值．

(2)某个函数f(x)的值域是B，且f(x)∈A的概率不小于0．6，试确定t的取值范围． 12集合A是由适合以下性质的函数f(x)组成的，对任的x≥0,f(x)∈[-2，4]，有f(x)在[0，+∞]上是增函数．

(1)试判断f1(x)=-2及f2(x)=4-6·()(x≥0)是否在集合A中?若不在集合A中，试说明理由； 答案：解析：（1）log2t-2=3?t=32;

(2) 对于(1)中你认为是集合A中的函数f(x)不等式f(x)+f(x+2)＜2f(x+1)是否对于任意的x≥D总成

立?证明你的结论．

答案：B=[2,12],由题意及概率的意义得log2t?2?0.6?8?log2t?12?28?t?212.即t∈[256,4096]. 12?2

12 集合A是由适合以下性质的函数f(x)组成的，对任意的x≥0，f(x)∈[-2，4]，有f(x)在[0，+8]上

地增函数。

（1） 试判断f1(x)=x-2及f2(x)=4-6·（）（x≥0）是否在集合A中？若不在集合A中，试说明理

由；

答案：解析：（1）函数f1(x)=x?2不在集合A中，这是因为当x=49>0,f1(49)=5>4,不满足条件f2(x)=4-6()x在集合A中。

（2）对于（1）中你认为是集合A中的函数f(x)不等式f(x)+f(x+2)<2f(x+1)是否对于任意的x≥D总成

立？证明你的结论？

答案：∵

f(x)+f(x+2)-2f(x+1)=4-61212x

19

11111111()x?4?6?()x?2?8?12()x?1?6?()x[2??1?()2]?6()x(?)?0.?f(x)?f(x?2)?2f(x?1)对于任意x22222224

≥0总成立.

13 已知函数f(x)=x2?ax?

x1(x＞0)．

(1)写出函数f(x)的单调区间，并指出在每一个单调区间内，函数是递增的还是递减的．(不必证明) 答案：f(x)=x?122?a在(0,]上递减,在[,??)上递增. 2x22

1)恒成立，∴a>2x1)]max, 2x (2)若不等式f(x)＞0对于x∈(0，+∞)恒成立，求实数a的取值范围； 答案：f(x)>0即a>-(x?

由（1）的结论知当x?[?(x?21时[?(x?)]max??2故a??2. 22x

-1-1(3)若f(x)(x≥1)的反函数f(x)，试求f(a+). 答案：根据反函数的意义，令x?

3941919?a?a?,得4x2?9x?2?0,解得x?(舍去).或x?2.?f?1(a?)?2. 2x44414 已知函数f(x)=x+ax+b定义在区间[-1，1]上，且f(0)=f(1)，又P(x1，y1)，q(x2，y2)是其图像

上任意两点(x1≠x2)．

(1)求证：f(x)的图像关于点(0，b)成中心对称图形；

33答案：∵f(0)=f(1), ∴b=1+a+b,得a=-1. ∴f(x)=x-x+b的图象可由y=x-x的图象向上（或向下）平移b

3（或-b ）个单位得到.又y=x-x是奇函数，其图象关于原点成中心对称图形，∴f(x) 的图象关于点

（0，b）成中心对称图形。

(2)设直线PQ的斜率为k，求证：|k|＜2．

3答案：∵点P（x1,y1）,Q(x2y2)在f(x)=x-x+b的图象上，

∴k=33y1?y2(x1?x1?b)?(x2?x2?b)22??x1?x2?x1x2?1. x1?x2x1?x2

222222又x1x2?[?1,1]x1?x2,?0?x1?x2?x1x2?3,从而?1?x1?x2?x1x2?1?2,?|k|?|x1?x2?x1x2?1|?2.

(3)若0≤x1<x2≤1，求证：|y1-y2|<1．

答案：∵0≤x1<x2≤1,且|y1-y2|=2|x1-x2|=-2(x1-x2)+2 ②

①+②得2|y1-y2|<2.故|y1-y2|<1.

20