高中数学向量知识点总结
1、向量的加法:
AB+BC=AC
设a=(x,y) b=(x',y')
则a+b=(x+x',y+y')
向量的加法满足平行四边形法则和三角形法则。
向量加法的性质:
交换律:
a+b=b+a
结合律:
(a+b)+c=a+(b+c)
a+0=0+a=a
2、向量的减法
AB-AC=CB
a-b=(x-x',y-y')
若a//b
则a=eb
则xy`-x`y=0·
若a垂直b
则a·b=0
则xx`+yy`=0
3、向量的乘法
设a=(x,y) b=(x',y')
用坐标计算向量的内积:a·b(点积)=x·x'+y·y'
a·b=|a|·|b|*cosθ
a·b=b·a
(a+b)·c=a·c+b·c
a·a=|a|的平方
向量的夹角记为∈[0,π]
Ax+By+C=0的方向向量a=(-B,A)
(a·b)·c≠a·(b·c)
a·b=a·c不可推出b=c
设P1、P2是直线上的两点,P是l上不同于P1、P2的任意一点。则存在一个实数 λ,使向量P1P=λ向量PP2,λ叫做点P分有向线段P1P2所成的比。
若P1(x1,y1),P2(x2,y2),P(x,y)
x=(x1+λx2)/(1+λ)
则有
y=(y1+λy2)/(1+λ)
我们把上面的式子叫做有向线段P1P2的定比分点公式
4、数乘向量
实数λ和向量a的乘积是一个向量,记作λa,且∣λa∣=∣λ∣*∣a∣,当λ>0时,与a同方向;当λ<0时,与a反方向。
实数λ叫做向量a的系数,乘数向量的几何意义时把向量a沿着的方向或反方向放大或缩小。
第二篇:高中数学平面向量知识点总结[1]
高中数学必修4之平面向量
知识点归纳
一.向量的基本概念与基本运算
1 向量的概念:
向量的概念:
①向量:既有大小又有方向的量 向量一般用
向量一般用 ……来表示,或用有向线段的起点与终点的大写字母表示,如:
……来表示,或用有向线段的起点与终点的大写字母表示,如: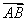
 几何表示法
几何表示法 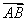 ,
, ;坐标表示法
;坐标表示法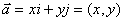
 向量的大小即向量的模(长度),记作|
向量的大小即向量的模(长度),记作|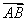 |
| 即向量的大小,记作|
即向量的大小,记作| |
|
向量不能比较大小,但向量的模可以比较大小.
②零向量:长度为0的向量,记为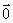 ,其方向是任意的,
,其方向是任意的,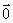 与任意向量平行
与任意向量平行 零向量
零向量 =
=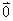
 |
| |=0
|=0 由于
由于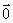 的方向是任意的,且规定
的方向是任意的,且规定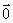 平行于任何向量,故在有关向量平行(共线)的问题中务必看清楚是否有“非零向量”这个条件.(注意与0的区别)
平行于任何向量,故在有关向量平行(共线)的问题中务必看清楚是否有“非零向量”这个条件.(注意与0的区别)
③单位向量:模为1个单位长度的向量
向量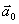 为单位向量
为单位向量 |
|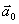 |=1
|=1
④平行向量(共线向量):方向相同或相反的非零向量 任意一组平行向量都可以移到同一直线上
任意一组平行向量都可以移到同一直线上 方向相同或相反的向量,称为平行向量
方向相同或相反的向量,称为平行向量 记作
记作 ∥
∥
 由于向量可以进行任意的平移(即自由向量),平行向量总可以平移到同一直线上,故平行向量也称为共线向量
由于向量可以进行任意的平移(即自由向量),平行向量总可以平移到同一直线上,故平行向量也称为共线向量
数学中研究的向量是自由向量,只有大小、方向两个要素,起点可以任意选取,现在必须区分清楚共线向量中的“共线”与几何中的“共线”、的含义,要理解好平行向量中的“平行”与几何中的“平行”是不一样的.
⑤相等向量:长度相等且方向相同的向量 相等向量经过平移后总可以重合,记为
相等向量经过平移后总可以重合,记为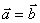
 大小相等,方向相同
大小相等,方向相同
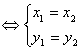

2 向量加法
向量加法
求两个向量和的运算叫做向量的加法
设 ,则
,则 +
+ =
=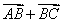 =
=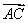

(1)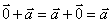 ;(2)向量加法满足交换律与结合律;
;(2)向量加法满足交换律与结合律;
向量加法有“三角形法则”与“平行四边形法则”:
(1)用平行四边形法则时,两个已知向量是要共始点的,和向量是始点与已知向量的始点重合的那条对角线,而差向量是另一条对角线,方向是从减向量指向被减向量
(2) 三角形法则的特点是“首尾相接”,由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和;差向量是从减向量的终点指向被减向量的终点
当两个向量的起点公共时,用平行四边形法则;当两向量是首尾连接时,用三角形法则.向量加法的三角形法则可推广至多个向量相加:
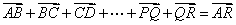 ,但这时必须“首尾相连”.
,但这时必须“首尾相连”.
3 向量的减法
向量的减法
① 相反向量:与 长度相等、方向相反的向量,叫做
长度相等、方向相反的向量,叫做 的相反向量
的相反向量
记作 ,零向量的相反向量仍是零向量
,零向量的相反向量仍是零向量
关于相反向量有: (i) =
= ; (ii)
; (ii)  +(
+( )=(
)=( )+
)+ =
=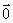 ;
;
(iii)若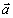 、
、 是互为相反向量,则
是互为相反向量,则 =
= ,
, =
= ,
, +
+ =
=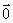

②向量减法:向量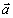 加上
加上 的相反向量叫做
的相反向量叫做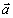 与
与 的差,
的差,
记作: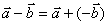
 求两个向量差的运算,叫做向量的减法
求两个向量差的运算,叫做向量的减法
③作图法: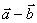 可以表示为从
可以表示为从 的终点指向
的终点指向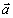 的终点的向量(
的终点的向量(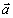 、
、 有共同起点)
有共同起点)
4 实数与向量的积:
实数与向量的积:
①实数λ与向量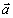 的积是一个向量,记作λ
的积是一个向量,记作λ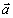 ,它的长度与方向规定如下:
,它的长度与方向规定如下:
(Ⅰ) ;
;
(Ⅱ)当 时,λ
时,λ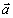 的方向与
的方向与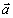 的方向相同;当
的方向相同;当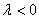 时,λ
时,λ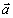 的方向与
的方向与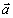 的方向相反;当
的方向相反;当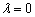 时,
时,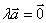 ,方向是任意的
,方向是任意的
②数乘向量满足交换律、结合律与分配律
5 两个向量共线定理:
两个向量共线定理:
向量 与非零向量
与非零向量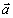 共线
共线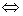 有且只有一个实数
有且只有一个实数 ,使得
,使得 =
=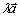

6 平面向量的基本定理:
平面向量的基本定理:
如果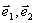 是一个平面内的两个不共线向量,那么对这一平面内的任一向量
是一个平面内的两个不共线向量,那么对这一平面内的任一向量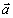 ,有且只有一对实数
,有且只有一对实数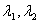 使:
使: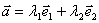 ,其中不共线的向量
,其中不共线的向量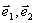 叫做表示这一平面内所有向量的一组基底
叫做表示这一平面内所有向量的一组基底
7 特别注意:
特别注意:
(1)向量的加法与减法是互逆运算
(2)相等向量与平行向量有区别,向量平行是向量相等的必要条件
(3)向量平行与直线平行有区别,直线平行不包括共线(即重合),而向量平行则包括共线(重合)的情况
(4)向量的坐标与表示该向量的有向线条的始点、终点的具体位置无关,只与其相对位置有关
学习本章主要树立数形转化和结合的观点,以数代形,以形观数,用代数的运算处理几何问题,特别是处理向量的相关位置关系,正确运用共线向量和平面向量的基本定理,计算向量的模、两点的距离、向量的夹角,判断两向量是否垂直等 由于向量是一新的工具,它往往会与三角函数、数列、不等式、解几等结合起来进行综合考查,是知识的交汇点
由于向量是一新的工具,它往往会与三角函数、数列、不等式、解几等结合起来进行综合考查,是知识的交汇点
例1 给出下列命题:
① 若| |=|
|=| |,则
|,则 =
= ;
;
② 若A,B,C,D是不共线的四点,则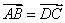 是四边形ABCD为平行四边形的充要条件;
是四边形ABCD为平行四边形的充要条件;
③ 若 =
= ,
, =
=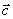 ,则
,则 =
=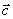 ,
,
④ =
= 的充要条件是|
的充要条件是| |=|
|=| |且
|且 //
// ;
;
⑤ 若 //
// ,
, //
//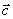 ,则
,则 //
//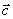 ,
,
其中正确的序号是 
解:①不正确.两个向量的长度相等,但它们的方向不一定相同.
② 正确.∵ 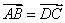 ,∴
,∴ 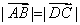 且
且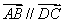 ,
,
又 A,B,C,D是不共线的四点,∴ 四边形 ABCD为平行四边形;反之,若四边形ABCD为平行四边形,则,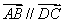 且
且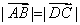 ,
,
因此,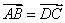 .
.
③ 正确.∵  =
= ,∴
,∴  ,
, 的长度相等且方向相同;
的长度相等且方向相同;
又 =
=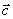 ,∴
,∴  ,
,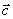 的长度相等且方向相同,
的长度相等且方向相同,
∴  ,
,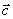 的长度相等且方向相同,故
的长度相等且方向相同,故 =
=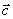 .
.
④ 不正确.当 //
// 且方向相反时,即使|
且方向相反时,即使| |=|
|=| |,也不能得到
|,也不能得到 =
= ,故|
,故| |=|
|=| |且
|且 //
// 不是
不是 =
= 的充要条件,而是必要不充分条件.
的充要条件,而是必要不充分条件.
⑤ 不正确.考虑 =
=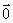 这种特殊情况.
这种特殊情况.
综上所述,正确命题的序号是②③.
点评:本例主要复习向量的基本概念.向量的基本概念较多,因而容易遗忘.为此,复习一方面要构建良好的知识结构,另一方面要善于与物理中、生活中的模型进行类比和联想.
例2 设A、B、C、D、O是平面上的任意五点,试化简:
①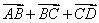 ,②
,②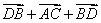 ③
③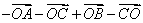
解:①原式= 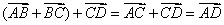
②原式= 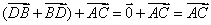
③原式= 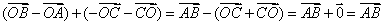
例3设非零向量 、
、 不共线,
不共线,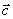 =k
=k +
+ ,
,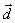 =
= +k
+k (kÎR),若
(kÎR),若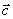 ∥
∥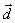 ,试求k
,试求k
解:∵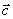 ∥
∥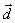
∴由向量共线的充要条件得: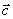 =λ
=λ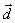 (λÎR)
(λÎR)
即 k +
+ =λ(
=λ( +k
+k ) ∴(k-λ)
) ∴(k-λ)  + (1-λk)
+ (1-λk)  =
= 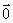
又∵ 、
、 不共线
不共线
∴由平面向量的基本定理 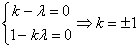
二.平面向量的坐标表示
1 平面向量的坐标表示:在直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量
平面向量的坐标表示:在直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量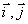 作为基底
作为基底 由平面向量的基本定理知,该平面内的任一向量
由平面向量的基本定理知,该平面内的任一向量 可表示成
可表示成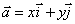 ,由于
,由于 与数对(x,y)是一一对应的,因此把(x,y)叫做向量
与数对(x,y)是一一对应的,因此把(x,y)叫做向量 的坐标,记作
的坐标,记作 =(x,y),其中x叫作
=(x,y),其中x叫作 在x轴上的坐标,y叫做在y轴上的坐标
在x轴上的坐标,y叫做在y轴上的坐标
(1)相等的向量坐标相同,坐标相同的向量是相等的向量
(2)向量的坐标与表示该向量的有向线段的始点、终点的具体位置无关,只与其相对位置有关
2 平面向量的坐标运算:
平面向量的坐标运算:
(1) 若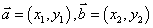 ,则
,则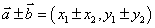
(2) 若 ,则
,则
(3) 若 =(x,y),则
=(x,y),则
 =(
=( x,
x,  y)
y)
(4) 若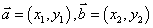 ,则
,则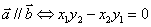
(5) 若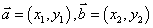 ,则
,则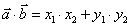
若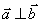 ,则
,则
3 向量的运算向量的加减法,数与向量的乘积,向量的数量(内积)及其各运算的坐标表示和性质
向量的运算向量的加减法,数与向量的乘积,向量的数量(内积)及其各运算的坐标表示和性质

例1 已知向量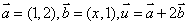 ,
,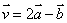 ,且
,且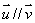 ,求实数
,求实数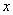 的值
的值
解:因为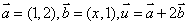 ,
,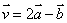
所以 ,
,
又因为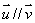
所以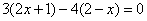 ,即
,即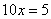
解得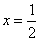
例2已知点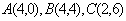 ,试用向量方法求直线
,试用向量方法求直线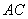 和
和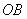 (
(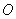 为坐标原点)交点
为坐标原点)交点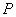 的坐标
的坐标
解:设 ,则
,则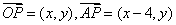
因为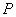 是
是 与
与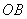 的交点
的交点
所以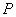 在直线
在直线 上,也在直线
上,也在直线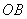 上
上
即得
由点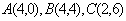 得,
得,
得方程组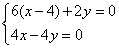
解之得
故直线 与
与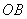 的交点
的交点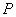 的坐标为
的坐标为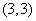

三.平面向量的数量积
1 两个向量的数量积:
两个向量的数量积:
已知两个非零向量 与
与 ,它们的夹角为
,它们的夹角为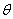 ,则
,则 ·
· =︱
=︱ ︱·︱
︱·︱ ︱cos
︱cos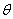
叫做 与
与 的数量积(或内积)
的数量积(或内积) 规定
规定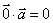

2 向量的投影:︱
向量的投影:︱ ︱cos
︱cos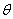 =
=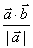 ∈R,称为向量
∈R,称为向量 在
在 方向上的投影
方向上的投影 投影的绝对值称为射影
投影的绝对值称为射影
3 数量积的几何意义:
数量积的几何意义:  ·
· 等于
等于 的长度与
的长度与 在
在 方向上的投影的乘积
方向上的投影的乘积
4 向量的模与平方的关系:
向量的模与平方的关系: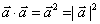

5 乘法公式成立:
乘法公式成立:
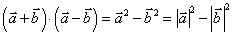 ;
;
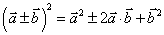
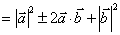
6 平面向量数量积的运算律:
平面向量数量积的运算律:
①交换律成立: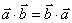
②对实数的结合律成立: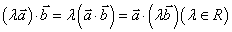
③分配律成立:
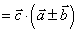
特别注意:(1)结合律不成立: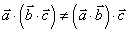 ;
;
(2)消去律不成立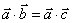
 不能得到
不能得到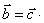
(3)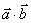 =0
=0 不能得到
不能得到 =
=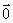 或
或 =
=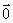

7 两个向量的数量积的坐标运算:
两个向量的数量积的坐标运算:
已知两个向量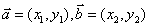 ,则
,则 ·
· =
=

8 向量的夹角:已知两个非零向量
向量的夹角:已知两个非零向量 与
与 ,作
,作 =
= ,
,  =
= ,则∠AOB=
,则∠AOB=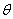 (
(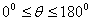 )叫做向量
)叫做向量 与
与 的夹角
的夹角
cos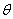 =
= =
=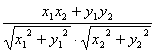

当且仅当两个非零向量 与
与 同方向时,θ=00,当且仅当
同方向时,θ=00,当且仅当 与
与 反方向时θ=1800,同时
反方向时θ=1800,同时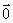 与其它任何非零向量之间不谈夹角这一问题
与其它任何非零向量之间不谈夹角这一问题
9 垂直:如果
垂直:如果 与
与 的夹角为900则称
的夹角为900则称 与
与 垂直,记作
垂直,记作 ⊥
⊥

10 两个非零向量垂直的充要条件:
两个非零向量垂直的充要条件:
 ⊥
⊥
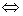
 ·
· =O
=O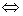

 平面向量数量积的性质
平面向量数量积的性质
例1 判断下列各命题正确与否:
(1)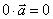 ;(2)
;(2)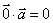 ;
;
(3)若 ,则
,则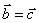 ;
;
⑷若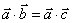 ,则
,则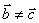 当且仅当
当且仅当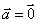 时成立;
时成立;
(5)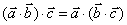 对任意
对任意 向量都成立;
向量都成立;
(6)对任意向量 ,有
,有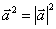

解:⑴错; ⑵对; ⑶错; ⑷错; ⑸ 错;⑹对
例2已知两单位向量 与
与 的夹角为
的夹角为 ,若
,若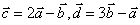 ,试求
,试求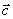 与
与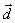 的夹角
的夹角
解:由题意,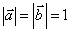 ,且
,且 与
与 的夹角为
的夹角为 ,
,
所以,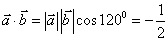 ,
,

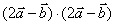
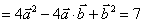 ,
,
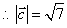 ,
,
同理可得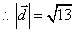
而
 ,
,
设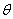 为
为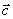 与
与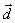 的夹角,
的夹角,
则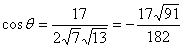

点评:向量的模的求法和向量间的乘法计算可见一斑
例3 已知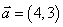 ,
,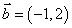 ,
,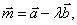
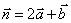 ,按下列条件求实数
,按下列条件求实数 的值
的值
(1)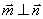 ;(2)
;(2) ;
;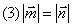
解: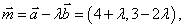

 (1)
(1)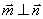
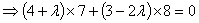
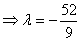 ;
;
(2)

 ;
;
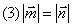
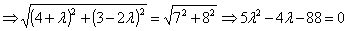
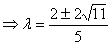

点评:此例展示了向量在坐标形式下的基本运算
-
高中数学平面向量知识点总结
高考圈让高考没有难报的志愿高中数学必修4之平面向量一向量的基本概念与基本运算1向量的概念向量既有大小又有方向的量向量不能比较大小但…
-
高中数学向量知识点总结
1向量的加法ABBCAC设axybx39y39则abxx39yy39向量的加法满足平行四边形法则和三角形法则向量加法的性质交换律a…
-
高中数学必修4平面向量知识点总结
高中数学必修4平面向量知识点归纳一向量的基本概念与基本运算1向量的概念向量既有大小又有方向的量向量一般用abc来表示或用有向线段的…
-
高中数学平面向量知识点总结
高中数学必修4之平面向量知识点归纳一.向量的基本概念与基本运算1、向量的概念:①向量:既有大小又有方向的量向量不能比较大小,但向量…
-
高中数学平面向量知识点总结及常见题型
平面向量一向量的基本概念与基本运算向量abc来表示或用有向线段的起点与终点的大写字母表示如ABABa坐标表示法axiyjxy向量的…
-
高中数学平面向量知识点总结
高中数学必修4之平面向量知识点归纳一.向量的基本概念与基本运算1、向量的概念:①向量:既有大小又有方向的量向量不能比较大小,但向量…
-
高中数学平面向量知识点总结
高中数学必修4之平面向量一.向量的基本概念与基本运算???①向量:既有大小又有方向的量向量一般用a,b,c??来表示,或用有向线段…
-
高中数学平面向量知识点总结
平面向量知识点知识点归纳一.向量的基本概念与基本运算1、向量的概念:①向量:既有大小又有方向的量向量不能比较大小,但向量的模可以比…
-
高中数学必修4平面向量知识点与典型例题总结(生)
《数学》必会基础题型——《平面向量》【基本概念与公式】【任何时候写向量时都要带箭头】1.向量:既有大小又有方向的量。记作:AB或a…
-
高一数学向量知识点归纳练习题
向量一、平面向量的加法和乘积rrrr1、向量加法的交换律:a?b?b?arrrrrr2、向量加法的结合律:(a?b)?c?a?(b…
-
备战高考--高中数学平面向量知识点总结
必修4平面向量一.向量的基本概念与基本运算???①向量:既有大小又有方向的量a,b,c??来表示,或用有向线段的起点与终点的大写字…