哈工大近代光学实验报告
《近代光学创新实验》
双曝光全息照相技术介绍
院(系) 英才学院
专 业 机械设计制造及其自动化
学 生
学 号
班 号
20##年6月
双曝光全息照相技术介绍
摘要:双曝光全息照相技术是指在拍摄静态全息图曝光过程中,如果拍摄物产生了微小位移(或微小形变),则这张全息图再现时在像的表面上就会产生若干条黑条纹,从而可以根据全息图片再现的物象条纹完成对拍摄物体表面,诸如形变、位移、振动等多种物理量的研究和测量工作。通过最近几年的发展,全息干涉测量法已经在无损检测、微小位移或振动的监测等领域得到了广泛的应用,成为全息照相技术的一个重要分支。
关键词:激光全息干涉技术;双爆光;测量
0 引言
双曝光法即在全息光路布局中,用一张全息底片分别对变形前后的物体进行两次全息照相。这时,物体在变形前后的两个光波波阵面相互重叠,固定在一张全息图中。如全息图用拍摄时的参考光照明,再现的干涉条纹图即表征物体在两次曝光之间的变形或位移。双曝光全息干涉法是简单易行的常用方法,可获得高反差的干涉条纹图。
自激光全息术发明以来,激光全息技术的应用领域和范围不断拓展,对相关技术和行业的影响越来越大,尤其是近年来随着激光全息技术与其它学科技术的综合运用,激光全息技术更展现了它的巨大应用前景。全息干涉测量技术是全息技术应用于实际的最早也是最主要的技术之一,它把普通的干涉测量同全息技术结合起来,有如下特点:
(1) 一般干涉测量只可用来测量形状比较简单的高度抛光表面的工件,而全息干涉测量能够对具有任意形状和粗糙表面的三维表面进行测量,精度可达光波波长数量级。
(2) 由于全息图再现的像具有三维性质,故用全息技术就可以通过干涉测量方法从许多不同视角去观察一个形状复杂的物体,一个干涉测量全息图就相当于用一般干涉测量进行的多次观察。
(3) 全息干涉测量可以对一个物体在两个不同时刻的状态进行对比,因而可以探测物体在一段时间内发生的任何改变。这样,将此一时刻物体与较早时刻的物体本身加以比较,在许多领域的应用中将有很大优点,特别是适用于任意形状和粗糙表面的测量。
(4) 全息干涉测量的不足之处是其测量范围小,仅几十微米左右。
目前,全息干涉测量技术在方法上先后发展了实时全息干涉法(单次曝光法)、双曝光全息干涉法、时间平均全息干涉法、双波长干涉法以及双脉冲频闪全息干涉法等。双曝光全息干涉测量法原理简单操作方便,是测定物体微小变形的有效方法。
1 实验原理
1) 基本原理 所有干涉仪的工作原理都是比较两个或多个波面的形状。双曝光法是将初始物光波面与变形以后的物光波面相比较。在记录过程中对一张全息干板作双曝光,一次是记录初始物光波(标准波面)的全息图;一次是记录变化以后的物光波(变形波面)的全息图。这两张全息图记录在同一张干板上,记录时顺序也可以颠倒。当用照明光波再现时,可再现出两个物光波面,这两个波面是相干的,因而观察到的是她们之间的干涉条纹。通过干涉条纹的分布情况,可以了解波面的变化。
双曝光法的记录与再现光路如图1所示。在底片平面上,参考光波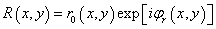 ,初始物光波
,初始物光波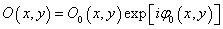 ,变形后的物光波
,变形后的物光波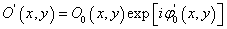 。
。
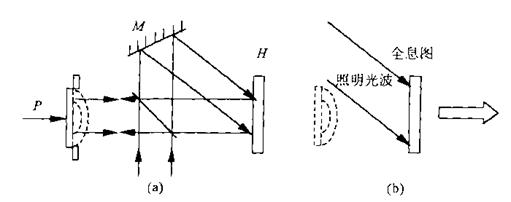
图1 双曝光全息图的记录与再现
假设两次曝光时间相同,则总的曝光光强为


在线性记录条件下,全息图的复振幅透过率正比于曝光光强
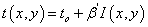
假设用参考光波照明全息图,如图1(b),则在全息图的透射光波中,与原始物光波和变形物光波有关的分量波为
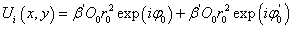
再现的原始物光波前和变形物光波前沿同一方向传播,产生干涉。这时干涉条纹的强度分布为

因为变形后的物光波前已经“冻结”在全息图中,在适当照明条件下就可以通过再现产生干涉条纹,从而给定量分析提供了很大的方便。[1]
2)几种典型光路 图2是透明物体的双曝光光路。用平行光照射物体,其透射光与参考光干涉产生全息图。一次曝光是初始状态的样品(或不放样品),另一次曝光时样品已发生变化(或放入样品)。
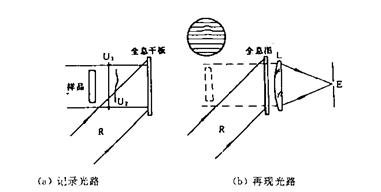
图2 透明物体的双曝光光路
参考光R用平面光波或球面波均可。物体用平行光照明时,可以得到像面全息图,即全息干板上记录的是两个波面干涉的像图全息图。再现时,有两种观察方式,一种如图2(b)所示,用原来的参考光R照明再现,在小孔E处可观察到整个物面上的条纹;另一种是根据像面全息的特点,可以用白光直接观察,在合适的方向上可以看到干涉条纹。暗纹是黑色的,亮纹是彩色的,角度改变时,条纹的彩色也在变化,但条纹的位置不变。
图3给出了另一种典型的双曝光光路,即漫射光照明的双曝光光路。通常用一块很薄的毛玻璃产生散射光,这样物体可以获得各种方向的照明。对于参考光同样可以用平面或球面光波。用这种方式所记录的双曝光全息图,再现时,可在原来记录光路中(挡住物光)再现,也可以用一细激光束从与参考光相反的方向照明,再现的原始像光波是发散的,可投射到屏上观察。
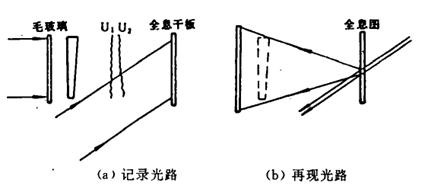
图3 漫射光照明的双曝光光路
2 双曝光全息照相技术应用
1) 双曝光法在平面物体的位移和变形测试方面的应用
用全息干涉法测量不透明物体表面的变化和位移时,可采用如图4所示光路。
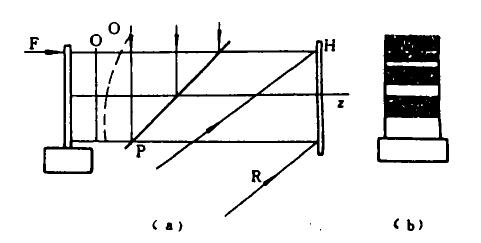
图4 平面物体位移和变形的双曝光光路
对于平面物体的位移和形变测量可采用平行光垂直照明的方式,如图4(a)所示,第一次曝光时,物体处于自由状态;第双曝光时,物体处于受力的状态,物体的位移是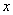 的函数,记作
的函数,记作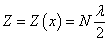 ;再现像的干涉条纹如图4(b)所示,N为条纹数目。
;再现像的干涉条纹如图4(b)所示,N为条纹数目。
2) 双曝光技术在光刻术方面的应用
光刻术是把超小线条刻印到半导体薄片上来制作复杂电路的技术,目前这些半导体电路正促使信息爆炸。这一技术是今天经典光学设计和制造的需求量最大的应用之一。光刻技术的进展对半导体工业的显著增长也有一定的贡献。半导体技术从粗糙的单个晶体管到由百万个晶体管很快将是十亿个晶体管组成的微处理器和记忆芯片非同寻常的发展是一段令人神往的历史。1979年,常规智能把光刻限制到1μm的分辨率,出现了1983年就被电子束成像系统所替代的情形,到1985年,这一估算修改为0.5μm的最小分辨率,又出现了1993年被X射线光刻技术取代的情形。今天,用光刻进行0.25μm生产刚刚开始,0.18μm似乎也有可能。但光刻一直是芯片生产成本的限制因素。光学投影光刻术显示出适于完成这一任务。根据瑞利标准,分辨率是由成像光的波长(λ)和投影透镜的数值孔径(NA)决定: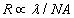 其中一部隐含但是重要的假设是:像质在这种分辨率下几乎完美。此外,图像的场尺寸必须很大。因此,改善光学分辨率的挑战是显而易见的。随着双曝光技术的不断发展,这一技术在改变光学分辨率上将有一定的应用前景。
其中一部隐含但是重要的假设是:像质在这种分辨率下几乎完美。此外,图像的场尺寸必须很大。因此,改善光学分辨率的挑战是显而易见的。随着双曝光技术的不断发展,这一技术在改变光学分辨率上将有一定的应用前景。
3) 曝光技术在制作光纤光栅器件上的应用
全息曝光法制作光纤光栅是人们早已采用的一种工艺,它首先通过分束器将光源分成两束等强光束,经过相同光程照射在光纤上形成强度周期性变化的干涉条纹,光纤折射率随光强周期性变化形成了光纤光栅,光栅周期T与入射波长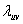 ,以及两干涉分束夹角
,以及两干涉分束夹角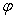 满足关系式
满足关系式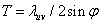 。全息曝光法的主要优点是光栅制作周期调谐方便灵活,Bragg波长可通过改变入射光束间夹角很容易进行调节。利用曝光技术制成的光纤光栅的应用领域正在不断取得新的进展,一方面主要集中于光纤光栅传感器;另一方面则是在光纤通讯领域。随着光纤光栅制作性能的不断完善,将会导致光纤技术及其相关领域的又一次新的革命。[2]
。全息曝光法的主要优点是光栅制作周期调谐方便灵活,Bragg波长可通过改变入射光束间夹角很容易进行调节。利用曝光技术制成的光纤光栅的应用领域正在不断取得新的进展,一方面主要集中于光纤光栅传感器;另一方面则是在光纤通讯领域。随着光纤光栅制作性能的不断完善,将会导致光纤技术及其相关领域的又一次新的革命。[2]
4) 双曝光法测量温度场
利用像面全息双曝光法测量温度场,采用像面全息记录,可以使物光聚焦在像面上,能够提高物光强度和干涉条纹的对比度,且可以在白光下再现。采用双曝光法,将像面全息的记录方式和双曝光法结合起来,具有非接触、精度高和全场同时测量等优点,且不会影响原有温度场的分布,可广泛应用于温度场的测量之中。
光学全息法用于温度场的测量,原理是温度的变化会引起空气折射率的变化,进而引起光程差的变化,产生干涉条纹。如果采用像面全息双曝光法,使物光通过温度场(参考光不经过温度场),温度场的变化则会引起折射率变化,使物光光程发生变化。温度相同的地方折射率相同,光程也相同。因此,每一个干涉条纹就是一条等温线,得到的干涉条纹则是一系列等温线,它反映了温度场的分布。
像面全息双曝光法是将像面全息的记录方式和双曝光的干涉方法结合起来的一种全息方法。对于漫射体的测量,反射光太弱,若以此作为物光波,很难满足干涉中物光强度和参考光强相差不大的条件,即使通过衰减参考光使其满足,也会严重影响干涉图的对比度和分辨率。采用像面全息可以增强物光波,满足干涉光束的强度要求,从而提高全息图的对比度。双曝光法通过对比初始物光波面和变化后的物光波面,观察二者之间的干涉条纹分布,测量物光波的变化。因此将像面全息的记录方式和双曝光的干涉方法结合起来,可以测量漫射体形变、位移、温度场的分布
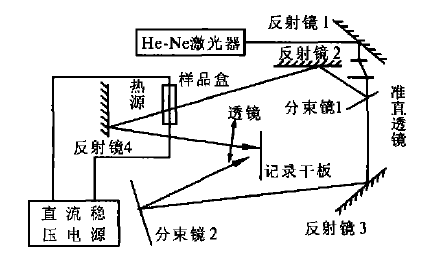
图5 双曝光法测量温度场
5) 双曝光法在无损检测中的应用
高压合成绝缘子是电力工业上的一种重要的基础元件,其制造水平对电力工业的发展有着非常重要的影响。由于其内部缺陷在外表很难看得出来,其硬度较低,粘合好后为细长件,刚性很差,对其进行在线检测一直是该行业面临的一道难题。寻找一套切实可行的检测方法,提供一种实用的检测设备,是高压合成绝缘子生产上的迫切需要。
由于试件在变形前后的两次曝光中,光路系统不变,两次曝光物光的光程差主要是由试件的变形所引起。利用全息干不涉法测量试件的位移灵敏度可达0.2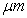 。因此,全息干涉法具有全场非接触测量和高灵敏度的优点,可以有效地用于无损检测。高压合成绝缘子在检测时,苦能给予适当加载,有内部缺陷的表面会呈现不均匀的变形。用全息干涉法测量表面位移场便可方便地揭示出其内部缺陷。[3]
。因此,全息干涉法具有全场非接触测量和高灵敏度的优点,可以有效地用于无损检测。高压合成绝缘子在检测时,苦能给予适当加载,有内部缺陷的表面会呈现不均匀的变形。用全息干涉法测量表面位移场便可方便地揭示出其内部缺陷。[3]
3 结论
全息干涉技术在应力分析、位移与振动冲击的测量,温度、流量、表面粗糙度的测量以及工业无损检测等方面有着广泛的应用,其重要特点是非接触、全场测量、高的测量精度等。
[1] 李田泽 二次曝光全息干涉技术及其应用 微细加工技术 1997 No.3
[2] 郭昕 用于微小位移测量的双曝光全息干涉计量 2005
[3] 林功顺 激光全息干涉技术在无损检测中的应用 郑州工业高专学报 1995.6
[4] 王健 高文斌 二次曝光全息干涉计量技术研究应力场 杭州大学电子科技大学学报 2006.8
第二篇:哈工大计算方法上机实验报告1
实验报告一
题目: 非线性方程求解
摘要:非线性方程的解析解通常很难给出,因此线性方程的数值解法就尤为重要。本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。
前言:(目的和意义)
掌握二分法与Newton法的基本原理和应用。
数学原理:
对于一个非线性方程的数值解法很多。在此介绍两种最常见的方法:二分法和Newton法。
对于二分法,其数学实质就是说对于给定的待求解的方程f(x),其在[a,b]上连续,f(a)f(b)<0,且f(x)在[a,b]内仅有一个实根x*,取区间中点c,若,则c恰为其根,否则根据f(a)f(c)<0是否成立判断根在区间[a,c]和[c,b]中的哪一个,从而得出新区间,仍称为[a,b]。重复运行计算,直至满足精度为止。这就是二分法的计算思想。
Newton法通常预先要给出一个猜测初值x0,然后根据其迭代公式
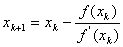
产生逼近解x*的迭代数列{xk},这就是Newton法的思想。当x0接近x*时收敛很快,但是当x0选择不好时,可能会发散,因此初值的选取很重要。另外,若将该迭代公式改进为
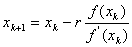
其中r为要求的方程的根的重数,这就是改进的Newton法,当求解已知重数的方程的根时,在同种条件下其收敛速度要比Newton法快的多。
程序设计:
本实验采用Matlab的M文件编写。其中待求解的方程写成function的方式,如下
function y=f(x);
y=-x*x-sin(x);
写成如上形式即可,下面给出主程序。
二分法源程序:
clear
%%%给定求解区间
b=1.5;
a=0;
%%%误差
R=1;
k=0;%迭代次数初值
while (R>5e-6) ;
c=(a+b)/2;
if f12(a)*f12(c)>0;
a=c;
else
b=c;
end
R=b-a;%求出误差
k=k+1;
end
x=c%给出解
Newton法及改进的Newton法源程序:
clear
%%%% 输入函数
f=input('请输入需要求解函数>>','s')
%%%求解f(x)的导数
df=diff(f);
%%%改进常数或重根数
miu=2;
%%%初始值x0
x0=input('input initial value x0>>');
k=0;%迭代次数
max=100;%最大迭代次数
R=eval(subs(f,'x0','x'));%求解f(x0),以确定初值x0时否就是解
while (abs(R)>1e-8)
x1=x0-miu*eval(subs(f,'x0','x'))/eval(subs(df,'x0','x'));
R=x1-x0;
x0=x1;
k=k+1;
if (eval(subs(f,'x0','x'))<1e-10);
break
end
if k>max;%如果迭代次数大于给定值,认为迭代不收敛,重新输入初值
ss=input('maybe result is error,choose a new x0,y/n?>>','s');
if strcmp(ss,'y')
x0=input('input initial value x0>>');
k=0;
else
break
end
end
end
k;%给出迭代次数
x=x0;%给出解
结果分析和讨论:
1. 用二分法计算方程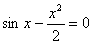 在[1,2]内的根。(
在[1,2]内的根。(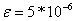 ,下同)
,下同)
计算结果为
x= 1.40441513061523;
f(x)= -3.797205105904311e-007;
k=18;
由f(x)知结果满足要求,但迭代次数比较多,方法收敛速度比较慢。
2. 用二分法计算方程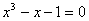 在[1,1.5]内的根。
在[1,1.5]内的根。
计算结果为
x= 1.32471847534180;
f(x)= 2.209494846194815e-006;
k=17;
由f(x)知结果满足要求,但迭代次数还是比较多。
3. 用Newton法求解下列方程
a) 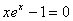 x0=0.5;
x0=0.5;
计算结果为
x= 0.56714329040978;
f(x)= 2.220446049250313e-016;
k=4;
由f(x)知结果满足要求,而且又迭代次数只有4次看出收敛速度很快。
b) 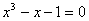 x0=1;
x0=1;
c) 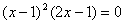 x0=0.45, x0=0.65;
x0=0.45, x0=0.65;
当x0=0.45时,计算结果为
x= 0.49999999999983;
f(x)= -8.362754932994584e-014;
k=4;
由f(x)知结果满足要求,而且又迭代次数只有4次看出收敛速度很快,实际上该方程确实有真解x=0.5。
当x0=0.65时,计算结果为
x= 0.50000000000000;
f(x)=0;
k=9;
由f(x)知结果满足要求,实际上该方程确实有真解x=0.5,但迭代次数增多,实际上当取x0〉0.68时,x≈1,就变成了方程的另一个解,这说明Newton法收敛与初值很有关系,有的时候甚至可能不收敛。
4. 用改进的Newton法求解,有2重根,取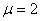
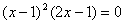 x0=0.55;并与3.中的c)比较结果。
x0=0.55;并与3.中的c)比较结果。
当x0=0.55时,程序死循环,无法计算,也就是说不收敛。改 时,结果收敛为
时,结果收敛为
x=0.50000087704286;
f(x)=4.385198907621127e-007;
k=16;
显然这个结果不是很好,而且也不是收敛至方程的2重根上。
当x0=0.85时,结果收敛为
x= 1.00000000000489;
f(x)= 2.394337647718737e-023;
k=4;
这次达到了预期的结果,这说明初值的选取很重要,直接关系到方法的收敛性,实际上直接用Newton法,在给定同样的条件和精度要求下,可得其迭代次数k=15,这说明改进后的Newton法法速度确实比较快。
结论:
对于二分法,只要能够保证在给定的区间内有根,使能够收敛的,当时收敛的速度和给定的区间有关,二且总体上来说速度比较慢。Newton法,收敛速度要比二分法快,但是最终其收敛的结果与初值的选取有关,初值不同,收敛的结果也可能不一样,也就是结果可能不时预期需要得结果。改进的Newton法求解重根问题时,如果初值不当,可能会不收敛,这一点非常重要,当然初值合适,相同情况下其速度要比Newton法快得多。
实验报告二
题目: Gauss列主元消去法
摘要:求解线性方程组的方法很多,主要分为直接法和间接法。本实验运用直接法的Guass消去法,并采用选主元的方法对方程组进行求解。
前言:(目的和意义)
1. 学习Gauss消去法的原理。
2. 了解列主元的意义。
3. 确定什么时候系数阵要选主元
数学原理:
由于一般线性方程在使用Gauss消去法求解时,从求解的过程中可以看到,若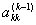 =0,则必须进行行交换,才能使消去过程进行下去。有的时候即使
=0,则必须进行行交换,才能使消去过程进行下去。有的时候即使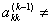 0,但是其绝对值非常小,由于机器舍入误差的影响,消去过程也会出现不稳定得现象,导致结果不正确。因此有必要进行列主元技术,以最大可能的消除这种现象。这一技术要寻找行r,使得
0,但是其绝对值非常小,由于机器舍入误差的影响,消去过程也会出现不稳定得现象,导致结果不正确。因此有必要进行列主元技术,以最大可能的消除这种现象。这一技术要寻找行r,使得
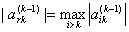
并将第r行和第k行的元素进行交换,以使得当前的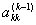 的数值比0要大的多。这种列主元的消去法的主要步骤如下:
的数值比0要大的多。这种列主元的消去法的主要步骤如下:
1. 消元过程
对k=1,2,…,n-1,进行如下步骤。
1) 选主元,记
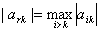
若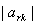 很小,这说明方程的系数矩阵严重病态,给出警告,提示结果可能不对。
很小,这说明方程的系数矩阵严重病态,给出警告,提示结果可能不对。
2) 交换增广阵A的r,k两行的元素。
 (j=k,…,n+1)
(j=k,…,n+1)
3) 计算消元
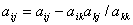 (i=k+1,…,n; j=k+1,……,n+1)
(i=k+1,…,n; j=k+1,……,n+1)
2. 回代过程
对k= n, n-1,…,1,进行如下计算
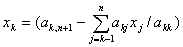
至此,完成了整个方程组的求解。
程序设计:
本实验采用Matlab的M文件编写。
Gauss消去法源程序:
clear
a=input('输入系数阵:>>\n')
b=input('输入列阵b:>>\n')
n=length(b);
A=[a b]
x=zeros(n,1);
%%%函数主体
for k=1:n-1;
%%%是否进行主元选取
if abs(A(k,k))%事先给定的认为有必要选主元的小数
yzhuyuan=1;
else yzhuyuan=0;
end
if yzhuyuan;
%%%%选主元
t=A(k,k);
for r=k+1:n;
if abs(A(r,k))>abs(t)
p=r;
else p=k;
end
end
%%%交换元素
if p~=k;
for q=k:n+1;
s=A(k,q);
A(k,q)=A(p,q);
A(p,q)=s;
end
end
end
%%%判断系数矩阵是否奇异或病态非常严重
if abs(A(k,k))< yipusilong
disp(‘矩阵奇异,解可能不正确’)
end
%%%%计算消元,得三角阵
for r=k+1:n;
m=A(r,k)/A(k,k);
for q=k:n+1;
A(r,q)=A(r,q)-A(k,q)*m;
end
end
end
%%%%求解x
x(n)=A(n,n+1)/A(n,n);
for k=n-1:-1:1;
s=0;
for r=k+1:n;
s=s+A(k,r)*x(r);
end
t=(A(k,n+1)-s)
x(k)=(A(k,n+1)-s)/A(k,k)
end
结果分析和讨论:
例:求解方程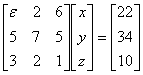 。其中
。其中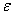 为一小数,当
为一小数,当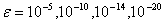 时,分别采用列主元和不列主元的Gauss消去法求解,并比较结果。
时,分别采用列主元和不列主元的Gauss消去法求解,并比较结果。
记Emax为求出的解代入方程后的最大误差,按要求,计算结果如下:
当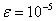 时,不选主元和选主元的计算结果如下,其中前一列为不选主元结果,后一列为选主元结果,下同。
时,不选主元和选主元的计算结果如下,其中前一列为不选主元结果,后一列为选主元结果,下同。
0.99999934768391 0.99999934782651
2.00000217421972 2.00000217391163
2.99999760859451 2.99999760869721
Emax= 9.301857062382624e-010,0
此时,由于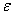 不是很小,机器误差就不是很大,由Emax可以看出不选主元的计算结果精度还可以,因此此时可以考虑不选主元以减少计算量。
不是很小,机器误差就不是很大,由Emax可以看出不选主元的计算结果精度还可以,因此此时可以考虑不选主元以减少计算量。
当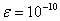 时,不选主元和选主元的计算结果如下
时,不选主元和选主元的计算结果如下
1.00001784630877 0.99999999999348
1.99998009720807 2.00000000002174
3.00000663424731 2.99999999997609
Emax= 2.036758973744668e-005,0
此时由Emax可以看出不选主元的计算精度就不好了,误差开始增大。
当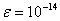 时,不选主元和选主元的计算结果如下
时,不选主元和选主元的计算结果如下
1.42108547152020 1.00000000000000
1.66666666666666 2.00000000000000
3.11111111111111 300000000000000
Emax= 0.70770085900503,0
此时由Emax可以看出,不选主元的结果应该可以说是不正确了,这是由机器误差引起的。
当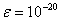 时,不选主元和选主元的计算结果如下
时,不选主元和选主元的计算结果如下
NaN 1
NaN 2
NaN 3
Emax=NaN, 0
不选主元时,程序报错:Warning: Divide by zero.。这是因为机器计算的最小精度为10-15,所以此时的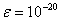 就认为是0,故出现了错误现象。而选主元时则没有这种现象,而且由Emax可以看出选主元时的结果应该是精确解。
就认为是0,故出现了错误现象。而选主元时则没有这种现象,而且由Emax可以看出选主元时的结果应该是精确解。
结论:
采用Gauss消去法时,如果在消元时对角线上的元素始终较大(假如大于10-5),那么本方法不需要进行列主元计算,计算结果一般就可以达到要求,否则必须进行列主元这一步,以减少机器误差带来的影响,使方法得出的结果正确。
实验报告三
题目: Rung现象产生和克服
摘要:由于高次多项式插值不收敛,会产生Runge现象,本实验在给出具体的实例后,采用分段线性插值和三次样条插值的方法有效的克服了这一现象,而且还取的很好的插值效果。
前言:(目的和意义)
1. 深刻认识多项式插值的缺点。
2. 明确插值的不收敛性怎样克服。
3. 明确精度与节点和插值方法的关系。
数学原理:
在给定n+1个节点和相应的函数值以后构造n次的Lagrange插值多项式,实验结果表明(见后面的图)这种多项式并不是随着次数的升高对函数的逼近越来越好,这种现象就是Rung现象。
解决Rung现象的方法通常有分段线性插值、三次样条插值等方法。
分段线性插值:
设在区间[a, b]上,给定n+1个插值节点
a=x01<…n=b
和相应的函数值y0,y1,…,yn,,求作一个插值函数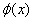 ,具有如下性质:
,具有如下性质:
1)  ,j=0,1,…,n。
,j=0,1,…,n。
2) 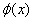 在每个区间[xi, xj]上是线性连续函数。则插值函数
在每个区间[xi, xj]上是线性连续函数。则插值函数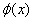 称为区间[a, b]上对应n个数据点的分段线性插值函数。
称为区间[a, b]上对应n个数据点的分段线性插值函数。
三次样条插值:
给定区间[a, b]一个分划
⊿:a=x01<…N=b
若函数S(x)满足下列条件:
1) S(x)在每个区间[xi, xj]上是不高于3次的多项式。
2) S(x)及其2阶导数在[a, b]上连续。则称S(x)使关于分划⊿的三次样条函数。
程序设计:
本实验采用Matlab的M文件编写。其中待插值的方程写成function的方式,如下
function y=f(x);
y=1/(1+25*x*x);
写成如上形式即可,下面给出主程序
Lagrange插值源程序:
n=input('将区间分为的等份数输入:\n');
s=[-1+2/n*[0:n]];%%%给定的定点,Rf为给定的函数
x=-1:0.01:1;
f=0;
for q=1:n+1;
l=1;%求插值基函数
for k=1:n+1;
if k~=q;
l=l.*(x-s(k))./(s(q)-s(k));
else
l=l;
end
end
f=f+Rf(s(q))*l;%求插值函数
end
plot(x,f,'r')%作出插值函数曲线
grid on
hold on
分段线性插值源程序
clear
n=input('将区间分为的等份数输入:\n');
s=[-1+2/n*[0:n]];%%%给定的定点,Rf为给定的函数
m=0;
hh=0.001;
for x=-1:hh:1;
ff=0;
for k=1:n+1;%%%求插值基函数
switch k
case 1
if x<=s(2);
l=(x-s(2))./(s(1)-s(2));
else
l=0;
end
case n+1
if x>s(n);
l=(x-s(n))./(s(n+1)-s(n));
else
l=0;
end
otherwise
if x>=s(k-1)&x<=s(k);
l=(x-s(k-1))./(s(k)-s(k-1));
else if x>=s(k)&x<=s(k+1);
l=(x-s(k+1))./(s(k)-s(k+1));
else
l=0;
end
end
end
ff=ff+Rf(s(k))*l;%%求插值函数值
end
m=m+1;
f(m)=ff;
end
%%%作出曲线
x=-1:hh:1;
plot(x,f,'r');
grid on
hold on
三次样条插值源程序:(采用第一边界条件)
clear
n=input('将区间分为的等份数输入:\n');
%%%插值区间
a=-1;
b=1;
hh=0.001;%画图的步长
s=[a+(b-a)/n*[0:n]];%%%给定的定点,Rf为给定的函数
%%%%第一边界条件Rf"(-1),Rf"(1)
v=5000*1/(1+25*a*a)^3-50/(1+25*a*a)^4;
for k=1:n;%取出节点间距
h(k)=s(k+1)-s(k);
end
for k=1:n-1;%求出系数向量lamuda,miu
la(k)=h(k+1)/(h(k+1)+h(k));
miu(k)=1-la(k);
end
%%%%赋值系数矩阵A
for k=1:n-1;
for p=1:n-1;
switch p
case k
A(k,p)=2;
case k-1
A(k,p)=miu(p+1);
case k+1
A(k,p)=la(p-1);
otherwise
A(k,p)=0;
end
end
end
%%%%求出d阵
for k=1:n-1;
switch k
case 1
d(k)=6*f2c([s(k) s(k+1) s(k+2)])-miu(k)*v;
case n-1
d(k)=6*f2c([s(k) s(k+1) s(k+2)])-la(k)*v;
otherwise
d(k)=6*f2c([s(k) s(k+1) s(k+2)]);
end
end
%%%%求解M阵
M=A\d';
M=[v;M;v];
%%%%
m=0;
f=0;
for x=a:hh:b;
if x==a;
p=1;
else
p=ceil((x-s(1))/((b-a)/n));
end
ff1=0;
ff2=0;
ff3=0;
ff4=0;
m=m+1;
ff1=1/h(p)*(s(p+1)-x)^3*M(p)/6;
ff2=1/h(p)*(x-s(p))^3*M(p+1)/6;
ff3=((Rf(s(p+1))-Rf(s(p)))/h(p)-h(p)*(M(p+1)-M(p))/6)*(x-s(p));
ff4=Rf(s(p))-M(p)*h(p)*h(p)/6;
f(m)=ff1+ff2+ff3+ff4 ;
end
%%%作出插值图形
x=a:hh:b;
plot(x,f,'k')
hold on
grid on
结果分析和讨论:
本实验采用函数 进行数值插值,插值区间为[-1,1],给定节点为
进行数值插值,插值区间为[-1,1],给定节点为
xj=-1+jh,h=0.1,j=0,…,n。下面分别给出Lagrange插值,三次样条插值,线性插值的函数曲线和数据表。图中只标出Lagrange插值的十次多项式的曲线,其它曲线没有标出,从数据表中可以看出具体的误差。
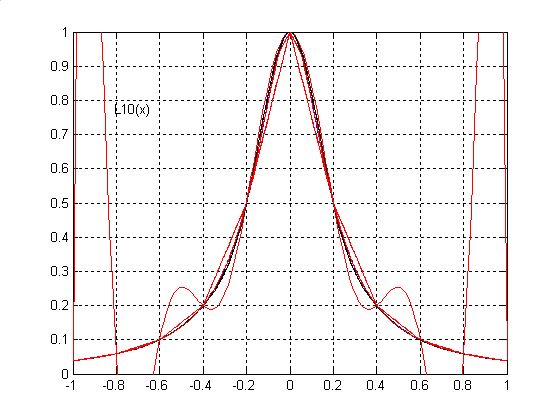
表中,L10(x)为Lagrange插值的10次多项式,S10(x),S40(x)分别代表n=10,40的三次样条插值函数,X10(x),X40(x)分别代表n=10,40的线性分段插值函数。
x f(x) L10(x) S10(x) S40(x) X10(x) X40(x)
-1.00000000000000 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154
-0.95000000000000 0.04244031830239 1.92363114971920 0.04240833151040 0.04244031830239 0.04355203619910 0.04244031830239
-0.90000000000000 0.04705882352941 1.57872099034926 0.04709697585458 0.04705882352941 0.04864253393665 0.04705882352941
-0.85000000000000 0.05245901639344 0.71945912837982 0.05255839923979 0.05245901639344 0.05373303167421 0.05245901639344
-0.80000000000000 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176
-0.75000000000000 0.06639004149378 -0.23146174989674 0.06603986172744 0.06639004149378 0.06911764705882 0.06639004149378
-0.70000000000000 0.07547169811321 -0.22619628906250 0.07482116198866 0.07547169811321 0.07941176470588 0.07547169811321
-0.65000000000000 0.08648648648649 -0.07260420322418 0.08589776360849 0.08648648648649 0.08970588235294 0.08648648648649
-0.60000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000
-0.55000000000000 0.11678832116788 0.21559187891257 0.11783833017713 0.11678832116788 0.12500000000000 0.11678832116788
-0.50000000000000 0.13793103448276 0.25375545726103 0.14004371555730 0.13793103448276 0.15000000000000 0.13793103448276
-0.45000000000000 0.16494845360825 0.23496854305267 0.16722724315883 0.16494845360825 0.17500000000000 0.16494845360825
-0.40000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000
-0.35000000000000 0.24615384615385 0.19058046675376 0.24054799403464 0.24615384615385 0.27500000000000 0.24615384615385
-0.30000000000000 0.30769230769231 0.23534659131080 0.29735691695860 0.30769230769231 0.35000000000000 0.30769230769231
-0.25000000000000 0.39024390243902 0.34264123439789 0.38048738140327 0.39024390243902 0.42500000000000 0.39024390243902
-0.20000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000
-0.15000000000000 0.64000000000000 0.67898957729340 0.65746969368431 0.64000000000000 0.62500000000000 0.64000000000000
-0.10000000000000 0.80000000000000 0.84340742982890 0.82052861660828 0.80000000000000 0.75000000000000 0.80000000000000
-0.05000000000000 0.94117647058824 0.95862704866073 0.94832323122810 0.94117647058824 0.87500000000000 0.94117647058824
0 1.00000000000000 1.00000000000000 1.00000000000000 1.00000000000000 1.00000000000000 1.00000000000000
0.05000000000000 0.94117647058824 0.95862704866073 0.94832323122810 0.94117647058824 0.87500000000000 0.94117647058824
0.10000000000000 0.80000000000000 0.84340742982890 0.82052861660828 0.80000000000000 0.75000000000000 0.80000000000000
0.15000000000000 0.64000000000000 0.67898957729340 0.65746969368431 0.64000000000000 0.62500000000000 0.64000000000000
0.20000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000
0.25000000000000 0.39024390243902 0.34264123439789 0.38048738140327 0.39024390243902 0.42500000000000 0.39024390243902
0.30000000000000 0.30769230769231 0.23534659131080 0.29735691695860 0.30769230769231 0.35000000000000 0.30769230769231
0.35000000000000 0.24615384615385 0.19058046675376 0.24054799403464 0.24615384615385 0.27500000000000 0.24615384615385
0.40000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000
0.45000000000000 0.16494845360825 0.23496854305267 0.16722724315883 0.16494845360825 0.17500000000000 0.16494845360825
0.50000000000000 0.13793103448276 0.25375545726103 0.14004371555730 0.13793103448276 0.15000000000000 0.13793103448276
0.55000000000000 0.11678832116788 0.21559187891257 0.11783833017713 0.11678832116788 0.12500000000000 0.11678832116788
0.60000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000
0.65000000000000 0.08648648648649 -0.07260420322418 0.08589776360849 0.08648648648649 0.08970588235294 0.08648648648649
0.70000000000000 0.07547169811321 -0.22619628906250 0.07482116198866 0.07547169811321 0.07941176470588 0.07547169811321
0.75000000000000 0.06639004149378 -0.23146174989674 0.06603986172744 0.06639004149378 0.06911764705882 0.06639004149378
0.80000000000000 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176
0.85000000000000 0.05245901639344 0.71945912837982 0.05255839923979 0.05245901639344 0.05373303167421 0.05245901639344
0.90000000000000 0.04705882352941 1.57872099034926 0.04709697585458 0.04705882352941 0.04864253393665 0.04705882352941
0.95000000000000 0.04244031830239 1.92363114971920 0.04240833151040 0.04244031830239 0.04355203619910 0.04244031830239
1.00000000000000 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154
从以上结果可以看到,用三次样条插值和线性分段插值,不会出现多项式插值是出现的Runge现象,插值效果明显提高。进一步说,为了提高插值精度,用三次样条插值和线性分段插值是可以增加插值节点的办法来满足要求,而用多项式插值函数时,节点数的增加必然会使多项式的次数增加,这样会引起数值不稳定,所以说这两种插值要比多项式插值好的多。而且在给定节点数的条件下,三次样条插值的精度要优于线性分段插值,曲线的光滑性也要好一些。
实验报告四
题目: 多项式最小二乘法
摘要:对于具体实验时,通常不是先给出函数的解析式,再进行实验,而是通过实验的观察和测量给出离散的一些点,再来求出具体的函数解析式。又因为测量误差的存在,实际真实的解析式曲线并不一定通过测量给出的所有点。最小二乘法是求解这一问题的很好的方法,本实验运用这一方法实现对给定数据的拟合。
前言:(目的和意义)
1. 学习使用最小二成法的原理
2. 了解法方程的特性
数学原理:
对于给定的测量数据(xi,fi)(i=1,2,…,n),设函数分布为
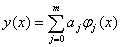
特别的,取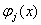 为多项式
为多项式
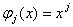 (j=0, 1,…,m)
(j=0, 1,…,m)
则根据最小二乘法原理,可以构造泛函
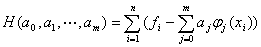
令
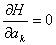 (k=0, 1,…,m)
(k=0, 1,…,m)
则可以得到法方程

求该解方程组,则可以得到解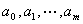 ,因此可得到数据的最小二乘解
,因此可得到数据的最小二乘解
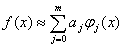
程序设计:
本实验采用Matlab的M文件编写。其中多项式函数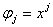 写成function的方式,如下
写成function的方式,如下
function y=fai(x,j)
y=1;
for i=1:j
y=x.*y;
end
写成如上形式即可,下面给出主程序。
多项式最小二乘法源程序
clear
%%%给定测量数据点(s,f)
s=[3 4 5 6 7 8 9];
f=[2.01 2.98 3.50 5.02 5.47 6.02 7.05];
%%%计算给定的数据点的数目
n=length(f);
%%%给定需要拟合的数据的最高次多项式的次数
m=10;
%%%程序主体
for k=0:m;
g=zeros(1,m+1);
for j=0:m;
t=0;
for i=1:n;%计算内积(fai(si),fai(si))
t=t+fai(s(i),j)*fai(s(i),k);
end
g(j+1)=t;
end
A(k+1,:)=g;%法方程的系数矩阵
t=0;
for i=1:n;%计算内积(f(si),fai(si))
t=t+f(i)*fai(s(i),k);
end
b(k+1,1)=t;
end
a=A\b%求出多项式系数
x=[s(1):0.01:s(n)]';
y=0;
for i=0:m;
y=y+a(i+1)*fai(x,i);
end
plot(x,y)%作出拟合成的多项式的曲线
grid on
hold on
plot(s,f,'rx') %在上图中标记给定的点
结果分析和讨论:
例 用最小二乘法处理下面的实验数据.

并作出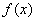 的近似分布图。
的近似分布图。
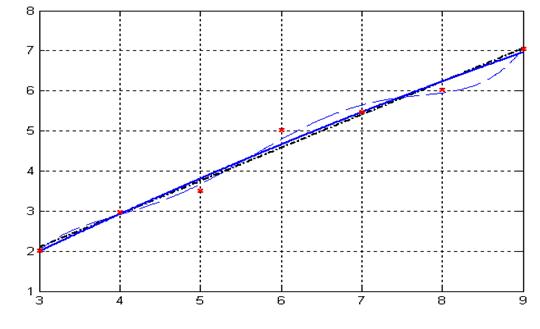
分别采用一次,二次和五次多项式来拟合数据得到相应的拟合多项式为:
y1=-0.38643+0.82750x;
y2=-1.03024+1.06893x-0.02012x2;
y5=-50.75309+51.53527x-19.65947x2+3.66585x3-0.32886x4+0.01137x5;
分别作出它们的曲线图,图中点划线为y1曲线,实线为y2曲线,虚线为y5曲线。’x’为给定的数据点。从图中可以看出并不是多项式次数越高越好,次数高了,曲线越能给定点处和实际吻合,但别的地方就很差了。因此,本例选用一次和两次的多项式拟合应该就可以了。
实验报告五
题目: Romberg积分法
摘要:对于实际的工程积分问题,很难应用Newton-Leibnitz公式去求解。因此应用数值方法进行求解积分问题已经有着很广泛的应用,本文基于Romberg积分法来解决一类积分问题。
前言:(目的和意义)
1. 理解和掌握Romberg积分法的原理;
2. 学会使用Romberg积分法;
3. 明确Romberg积分法的收敛速度及应用时容易出现的问题。
数学原理:
考虑积分 ,欲求其近似值,通常有复化的梯形公式、Simpsion公式和Cotes公式。但是给定一个精度,这些公式达到要求的速度很缓慢。如何提高收敛速度,自然是人们极为关心的课题。为此,记T1,k为将区间[a,b]进行2k等分的复化的梯形公式计算结果,记T2,k为将区间[a,b]进行2k等分的复化的Simpsion公式计算结果,记T3,k为将区间[a,b]进行2k等分的复化的Cotes公式计算结果。根据Richardson外推加速方法,可以得到收敛速度较快的Romberg积分法。其具体的计算公式为:
,欲求其近似值,通常有复化的梯形公式、Simpsion公式和Cotes公式。但是给定一个精度,这些公式达到要求的速度很缓慢。如何提高收敛速度,自然是人们极为关心的课题。为此,记T1,k为将区间[a,b]进行2k等分的复化的梯形公式计算结果,记T2,k为将区间[a,b]进行2k等分的复化的Simpsion公式计算结果,记T3,k为将区间[a,b]进行2k等分的复化的Cotes公式计算结果。根据Richardson外推加速方法,可以得到收敛速度较快的Romberg积分法。其具体的计算公式为:
1. 准备初值,计算
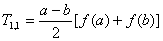
2. 按梯形公式的递推关系,计算

3. 按Romberg积分公式计算加速值
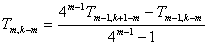 m=2,…,k
m=2,…,k
4. 精度控制。对给定的精度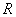 ,若
,若

则终止计算,并取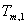 为所求结果;否则返回2重复计算,直至满足要求的精度为止。
为所求结果;否则返回2重复计算,直至满足要求的精度为止。
程序设计:
本实验采用Matlab的M文件编写。其中待积分的函数写成function的方式,例如如下
function yy=f(x,y);
yy=x.^3;
写成如上形式即可,下面给出主程序
Romberg积分法源程序
%%% Romberg积分法
clear
%%%积分区间
b=3;
a=1;
%%%精度要求
R=1e-5;
%%%应用梯形公式准备初值
T(1,1)=(b-a)*(f(b)+f(a))/2;
T(1,2)=T(1,1)/2+(b-a)/2*f((b+a)/2);
T(2,1)=(4*T(1,2)-T(1,1))/(4-1);
j=2;
m=2;
%%%主程序体%%%
while(abs(T(m,1)-T(m-1,1))>R);%%%精度控制
j=j+1;
s=0;
for p=1:2^(j-2);
s=s+f(a+(2*p-1)*h/(2^(j-1)));
end
T(1,j)=T(1,j-1)/2+h*s/(2^(j-1)); %%%梯形公式应用
for m=2:j;
k=(j-m+1);
T(m,k)=((4^(m-1))*T(m-1,k+1)-T(m-1,k))/(4^(m-1)-1);
end
end
%%%给出 Romberg积分法的函数表
I=T(m,1)
结果分析和讨论:
进行具体的积分时,精度取R=1e-8。
1. 求积分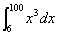 。精确解I= 24999676。
。精确解I= 24999676。
运行程序得Romberg积分法的函数表为
1.0e+007 *
4.70101520000000 3.05022950000000 2.63753307500000
2.49996760000000 2.49996760000000 0
2.49996760000000 0 0
由函数表知Romberg积分给出的结果为2.4999676*10^7,与精确没有误差,
精度很高。
2. 求积分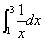 。精确解I=ln3= 1.09861228866811。
。精确解I=ln3= 1.09861228866811。
运行程序得Romberg积分法的函数表为
1.33333333333333 1.16666666666667 1.11666666666667 1.10321067821068 1.09976770156303 1.09890151516846 1.09868461878559
1.11111111111111 1.10000000000000 1.09872534872535 1.09862004268048 1.09861278637027 1.09861231999130 0
1.09925925925926 1.09864037197371 1.09861302227749 1.09861230261625 1.09861228889937 0 0
1.09863054836600 1.09861258815533 1.09861229119306 1.09861228868164 0 0 0
1.09861251772313 1.09861229002850 1.09861228867179 0 0 0 0
1.09861228980593 1.09861228867046 0 0 0 0 0
1.09861228867019 0 0 0 0 0 0
从积分表中可以看出程序运行的结果为1.09861228867019,取8位有效数字,满足要求。
3. 求积分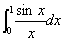 。
。
直接按前面方法进行积分,会发现系统报错,出现了0为除数的现象。出现这种情况的原因就是当x=0时,被积函数分母出现了0,如果用一个适当的小数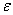 (最好不要小于程序给定的最小误差值,但是不能小于机器的最大精度)来代替,可以避免这个问题。本实验取
(最好不要小于程序给定的最小误差值,但是不能小于机器的最大精度)来代替,可以避免这个问题。本实验取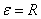 ,可得函数表为:
,可得函数表为:
0.92073548319659 0.93979327500190 0.94451351171417 0.94569085359489 0.94598501993743
0.94614587227034 0.94608692395160 0.94608330088846 0.94608307538495 0
0.94608299406368 0.94608305935092 0.94608306035138 0 0
0.94608306038722 0.94608306036726 0 0 0
0.94608306036718 0 0 0 0
故该函数的积分为0.94608306036718,取8位有效数字。
4. 求积分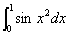
本题的解析解很难给出,但运用Romberg积分可以很容易给出近似解,函数表为:
0.42073549240395 0.33406972582924 0.31597536075922 0.31168023948094 0.31062036680949 0.31035626065456
0.30518113697100 0.30994390573588 0.31024853238818 0.31026707591900 0.31026822526959 0
0.31026142365354 0.31026884083167 0.31026831215439 0.31026830189296 0 0
0.31026895856465 0.31026830376269 0.31026830173008 0 0 0
0.31026830119484 0.31026830172211 0 0 0 0
0.31026830172262 0 0 0 0 0
故该函数的积分为0.31026830172262,取8位有效数字。
结论:
Romberg积分通常要求被积函数在积分区间上没有奇点。如有奇点,且奇点为第一间断点,那么采用例3的方法,还是能够求出来的,否则,必须采用其它的积分方法。当然,Romberg积分的收敛速度还是比较快的。
实验报告六
题目: 常微分方程初值问题的数值解法
摘要:本实验主要采用经典四阶的R-K方法和四阶Adams预测-校正方法来求解常微分方程的数值解。
前言:(目的和意义)
通过编写程序,进行上机计算,使得对常微分方程初值问题的数值解法有更深刻的理解,掌握单步法和线性多步法是如何进行实际计算的及两类方法的适用范围和优缺点,特别是对这两类方法中最有代表性的方法:R-K方法和Adams方法及预测-校正方法有更好的理解。通过这两种方法的配合使用,掌握不同的方法如何配合在一起,解决实际问题。
数学原理:
对于一阶常微分方程初值问题
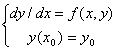 (1)
(1)
的数值解法是近似计算中很中的一部分。
常微分方程的数值解法通常就是给出定义域上的n个等距节点,求出所对应的函数值yn。通常其数值解法可分为两大类:
1. 单步法:这类方法在计算yn+1的值时,只需要知道xn+1、xn和yn即可,就可算出。这类方法典型有欧拉法和R-K法。
2. 多步法:这类方法在计算yn+1的值时,除了需要知道xn+1、xn和yn值外,还需要知道前k步的值。典型的方法如Adams法。
经典的R-K法是一个四阶的方法。它最大的优点就是它是单步法,精度高,计算过程便于改变步长。其缺点也很明显,计算量大,每前进一步就要计算四次函数值f。它的具体的计算公式如式(2)所示。
四阶Adams预测-校正方法是一个线性多步法,它是由Adams显式公式
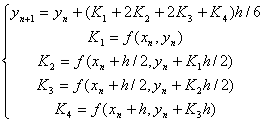 (2)
(2)
和隐式公式组成,其计算公式如式(3)所示。
预测 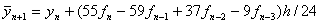 (3a)
(3a)
求导 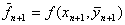 (3b)
(3b)
校正 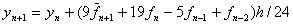 (3c)
(3c)
求导 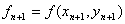 (3d)
(3d)
将局部截断误差用预测值和校正值来表示,在预测和校正的公式中分别以它们各自的阶段误差来进行弥补,可期望的到精度更高的修正的预测-校正公式为:
预测 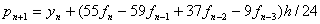
修正 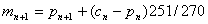
求导 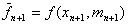
校正 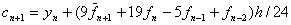
修正 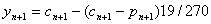
求导 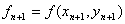
由于开始时无预测值和校正值可以利用,故令p0=c0=0,以后按上面进行计算。此方法的优点是可以减少计算量;缺点是它不是自开始的,需要先知道前面的四个点的值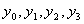 ,因此不能单独使用。另外,它也不便于改变步长。
,因此不能单独使用。另外,它也不便于改变步长。
程序设计:
本实验采用Matlab的M文件编写。其中待求的微分方程写成function的方式,如下
function yy=g(x,y);
yy=-x*x-y*y;
写成如上形式即可,下面给出主程序。
经典四阶的R-K方法源程序
clear
%%%步长选取
h=0.1;
%%%初始条件,即x=0时,y=1。
y(1)=1;
%%%求解区间
a=0;
b=2;
%%%迭代公式
for x=a:h:b-h;
k1=g(x,y((x-a)/h+1));%%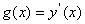 ,下同。
,下同。
k2=g(x+h/2,y((x-a)/h+1)+h/2*k1);
k3=g(x+h/2,y((x-a)/h+1)+h/2*k2);
k4=g(x+h,y((x-a)/h+1)+h*k3);
y((x-a)/h+2)=y((x-a)/h+1)+h*(k1+2*k2+2*k3+k4)/6;
end
四阶Adams预测-校正方法源程序
%%%步长选取
h=0.1;
%%%初始条件
y(1)=1;
%%%求解区间
a=0;
b=2;
%%%应用RK迭代公式计算初始值y0,y1,y2,y3
for x=a:h:a+2*h;
k1=g(x,y((x-a)/h+1));
k2=g(x+h/2,y((x-a)/h+1)+h/2*k1);
k3=g(x+h/2,y((x-a)/h+1)+h/2*k2);
k4=g(x+h,y((x-a)/h+1)+h*k3);
y((x-a)/h+2)=y((x-a)/h+1)+h*(k1+2*k2+2*k3+k4)/6;
end
%%%应用预测校正法求解
c(4)=0;%%%校正初值
p(4)=0;%%%预测初值
f(1)=g(a+0*h,y(1));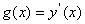 ,且将该值存在数组f中。
,且将该值存在数组f中。
f(2)=g(a+1*h,y(2));
f(3)=g(a+2*h,y(3));
f(4)=g(a+3*h,y(4));
for n=4:(b-a)/h;
%%%P预测
p(n+1)=y(n)+h/24*(55*f(n)-59*f(n-1)+37*f(n-2)-9*f(n-3));
%%%M修正
m(n+1)=p(n+1)+251/270*(c(n)-p(n));
%%%E求导
f(n+1)=g(a+(n+1-1)*h,m(n+1));
%%%C校正
c(n+1)=y(n)+h/24*(9*f(n+1)+19*f(n)-5*f(n-1)+f(n-2));
%%%M修正
y(n+1)=c(n+1)-19/270*(c(n+1)-p(n+1));
%%%E求导
f(n+1)=g(a+(n+1-1)*h,y(n+1));
end
结果分析和讨论:
计算实例一:对初值问题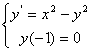 取步长h=0.1;计算在[-1,0]上的数值解。
取步长h=0.1;计算在[-1,0]上的数值解。
在计算机上,运用所编的程序进行了运算,结果如下,其中第一列为在区间上的等分点,第二列为运用R-K法的计算结果,第三列为Adams预测-校正法计算结果。由于本题的解析解很难求出,无法看出精度如何,为此进行第二实例计算。
第一实例计算结果
-1.00000000000000 0 0
-0.90000000000000 0.09004735746240 0.09004735746240
-0.80000000000000 0.16072688390128 0.16072688390128
-0.70000000000000 0.21348265038268 0.21348265038268
-0.60000000000000 0.25036836954459 0.25036768670937
-0.50000000000000 0.27377524760451 0.27377644362732
-0.40000000000000 0.28622191831814 0.28622489850956
-0.30000000000000 0.29021334157377 0.29021772444822
-0.20000000000000 0.28816017093689 0.28816545338237
-0.10000000000000 0.28234366396114 0.28234937949911
0 0.27491051923462 0.27491630159737
计算实例二:对初值问题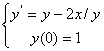 取步长h=0.1;计算在[0,1.5]上的数值解。本题的解析解为
取步长h=0.1;计算在[0,1.5]上的数值解。本题的解析解为 。
。
同样在计算机上,运用所编的程序进行了运算,结果如下,其中第一列为在区间上的等分点,第二列为运用R-K法的计算结果,第三列为Adams预测-校正法计算结果,第四列为精确解。
第二实例计算结果
0 1.00000000000000 1.00000000000000 1.00000000000000
0.10000000000000 1.09544553169309 1.09544553169309 1.09544511501033
0.20000000000000 1.18321674550599 1.18321674550599 1.18321595661992
0.30000000000000 1.26491222834039 1.26491222834039 1.26491106406735
0.40000000000000 1.34164235375037 1.34163505213867 1.34164078649987
0.50000000000000 1.41421557789009 1.41420723934048 1.41421356237310
0.60000000000000 1.48324222277199 1.48323305700166 1.48323969741913
0.70000000000000 1.54919645230214 1.54918577363467 1.54919333848297
0.80000000000000 1.61245534965899 1.61244282116642 1.61245154965971
0.90000000000000 1.67332465901626 1.67330987517170 1.67332005306815
1.00000000000000 1.73205636516557 1.73203885072786 1.73205080756888
1.10000000000000 1.78886106772579 1.78884027572849 1.78885438199983
1.20000000000000 1.84391691853791 1.84389219922183 1.84390889145858
1.30000000000000 1.89737622177080 1.89734679793772 1.89736659610103
1.40000000000000 1.94937040329812 1.94933534308208 1.94935886896179
1.50000000000000 2.00001381661027 1.99997200061724 2.00000000000000
根据计算结果,发现两种方法的结果与精确解很接近,精度均达到5位有效数字,但是R-K法运算是占用的内存要比Adams预测-校正法多,即其对计算机的要求要高一些,这与理论分析吻合。当然,四阶Adams预测-校正法的启动要由R-K法给出,即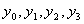 的值需预先知道。
的值需预先知道。
-
哈工大数电实验报告
HarbinInstituteofTechnology数字逻辑电路与系统课程名称院系班级哈尔滨工业大学20xx年11月实验二时序逻…
-
Java程序设计实验报告 哈工大
Java语言基础实验指导报告书20xx20xx年秋季学期使用班级姓名计算机科学与技术学院实验一Java编程开发环境一实验学时1学时…
-
哈工大数据库实验报告-实验一
数据库系统应用实验报告1班号学号姓名所用实验数据表给出创建表的sql语句createtable学院学院号char2NOTNULLU…
-
哈工大微波实验报告
电磁场与微波技术实验报告HarbinInstituteofTechnology电磁场与微波技术实验报告课程名称电磁场与微波技术设计…
-
哈工大倒立摆实验报告
研究生自动控制专业实验地点:A区主楼518房间平面二级倒立摆系统实验报告哈工大航天学院控制科学实验室平面二级倒立摆控制系统实验报告…
- 哈工大大物实验--空气中声速的测量实验报告
-
哈工大数字信号处理实验报告
数字信号处理实验报告学院航天学院班级12学号姓名实验一用FFT作谱分析实验目的1进一步加深DFT算法原理和基本性质的理解因为FFT…
-
哈工大电磁场与电磁波实验报告
电磁场与电磁波实验报告班级学号姓名同组人实验一电磁波的反射实验1实验目的任何波动现象无论是机械波光波无线电波在波前进的过程中如遇到…
-
哈工大现代控制理论实验报告一
现代控制理论实验报告HarbinInstituteofTechnology现代控制理论基础上机实验一亚微米超精密车床振动控制系统的…
-
哈工大 物理实验 数码照相报告(完美版)
实验报告样本电子稿大学物理实验实验二十四数码照相技术基础学号1110810711班号1108107姓名韩星合作者郑帅相机编号No2…
-
哈工大数值分析上机实验报告 20xx年
实验报告一题目Gauss列主元消去法摘要求解线性方程组的方法很多主要分为直接法和间接法本实验运用直接法的Guass消去法并采用选主…