实验3弦线上驻波实验
实验3弦线上驻波实验
一 实验目的
1.观察在弦上形成的驻波,并用实验确定弦线振动时驻波波长与张力的关系;
2.在弦线张力不变时,用实验确定弦线振动时驻波波长与振动频率的关系;
3.学习对数作图或最小二乘法进行数据处理。
二 实验仪器
FD-SWE-II 弦线上驻波实验仪1套
弦线 1根
砝码与砝码盘1套
三 实验原理
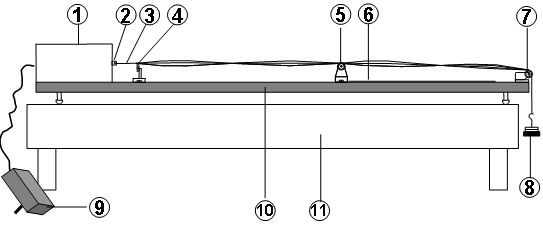
图1 仪器结构图
1、可调频率数显机械振动源;2、振动簧片;3、弦线;4、可动支架;5、可动刀口支架;6、标尺;7、固定滑轮;8、砝码与砝码盘;9、变压器;10、实验平台;11、实验桌
如图1一根线密度为 的拉紧的弦线,一端与振源相连,另一端跨过滑轮挂上一定质量的砝码,使其受张力为
的拉紧的弦线,一端与振源相连,另一端跨过滑轮挂上一定质量的砝码,使其受张力为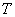 。这样,在振源的带动下, ④—⑤之间可观察到明显的驻波,若波源的振动频率为
。这样,在振源的带动下, ④—⑤之间可观察到明显的驻波,若波源的振动频率为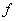 ,横波波长为
,横波波长为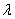 ,弦线密度为
,弦线密度为 ,弦线受张力为
,弦线受张力为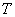 则它们之间满足如下关系:
则它们之间满足如下关系:
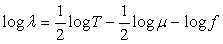 (1)
(1)
分析:如果固定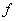 、
、 ,改变
,改变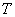 ,并测出各相应波长
,并测出各相应波长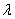 ,作log
,作log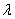 -log
-log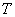 图,若得一直线,计算其斜率值(如为
图,若得一直线,计算其斜率值(如为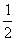 ),则证明了
),则证明了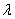 ∝
∝ 的关系成立。如果固定μ、
的关系成立。如果固定μ、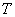 ,改变
,改变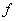 ,测出各相应波长
,测出各相应波长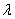 ,作log
,作log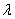 -log
-log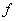 图,如得一斜率为-1的直线就验证了
图,如得一斜率为-1的直线就验证了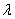 ∝
∝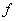 -1。本实验就是验证以上两项是否成立。
-1。本实验就是验证以上两项是否成立。
弦线上的波长可利用驻波原理测量。当两个振幅和频率相同的相干波在同一直线上相向传播时,其所叠加而成的波称为驻波,一维驻波是波干涉中的一种特殊情形。在弦线上出现许多静止点,称为驻波的波节。相邻两波节间的距离为半个波长。
四 实验步骤
A、验证横波的波长与弦线中的张力的关系
1、实验时,将变压器(黑色壳)输入插头与220V交流电源接通,输出端(五芯航空线)与主机上的航空座相连接。打开数显振动源面板上的电源开关①(振动源面板如图2所示)。面板上数码管⑤显示振动源振动频率×××.××Hz。根据需要按频率调节②中▲(增加频率)或▼(减小频率)键,改变振动源的振动频率,调节面板上幅度调节旋钮④,使振动源有振动输出;当不需要振动源振动时,可按面板上复位键③复位,数码管显示全部清零。

图2 振动源面板图
1、电源开关 2、频率调节 3、复位键 4、幅度调节 5、频率指示
2、在某些频率(60Hz附近),由于振动簧片共振使振幅过大,此时应逆时针旋转面板上的旋钮以减小振幅,便于实验进行(最好避开共振点做实验)。不在共振频率点工作时,可调节面板上幅度旋钮④到输出最大。
3、固定一个波源振动的频率(一般取为100Hz,若振动振幅太小,可将频率取小些,比如90Hz),在砝码盘上添加不同质量的砝码,以改变同一弦上的张力T。每改变一次张力(即增加一次砝码),均要左右移动可动刀口支架④(保持在第一波节点)和可动刀口⑤的位置,使弦线出现振幅较大而稳定的驻波。用实验平台⑩上的标尺⑥测量 值,记录振动频率、砝码质量、产生整数倍半波长的弦线长度及半波波数,根据式(3)算出波长
值,记录振动频率、砝码质量、产生整数倍半波长的弦线长度及半波波数,根据式(3)算出波长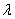 ,作log
,作log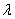 -logT图,求其斜率。
-logT图,求其斜率。
B、验证横波的波长与波源振动频率的关系
在砝码盘上放上3块质量为45g的砝码,以固定弦线上所受的张力T,改变波源振动的频率f,用驻波法测量各相应的波长,作log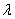 -log
-log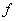 图,求其斜率。最后总结出弦线上波传播的规律。
图,求其斜率。最后总结出弦线上波传播的规律。
【实验数据】(注:以下数据不作为仪器验收标准,仅供实验时参考)
1、验证横波的波长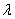 与弦线中的张力
与弦线中的张力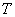 的关系(各砝码质量不一定严格等于45g,故需分别用分析天平测量)
的关系(各砝码质量不一定严格等于45g,故需分别用分析天平测量)
波源振动频率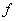 =100.00Hz;
=100.00Hz;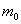 为挂钩的质量42.46g,L为产生驻波的弦线长度,
为挂钩的质量42.46g,L为产生驻波的弦线长度,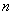 为在L长度内半波的波数,实验结果如表1所示。
为在L长度内半波的波数,实验结果如表1所示。
表1 给定频率的实验数据表
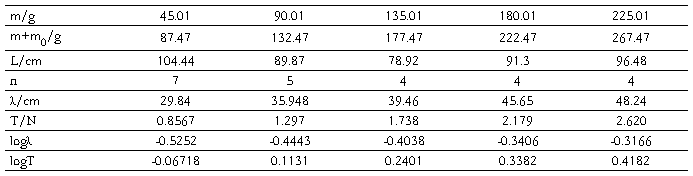
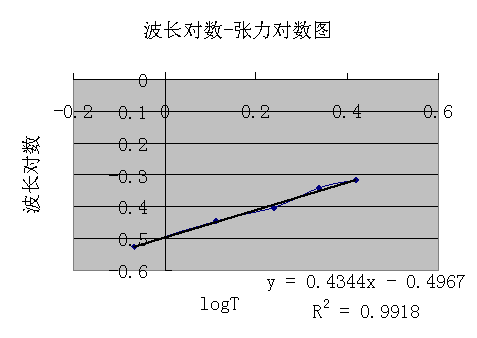
图3 波长对数-张力对数关系图
经最小二乘法拟合得log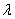 -log
-log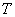 的斜率为:0.4344,相关系数为:0.99
的斜率为:0.4344,相关系数为:0.99
2、验证横波的波长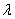 与波源振动频率
与波源振动频率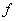 的关系
的关系
砝码加上挂钩的总质量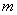 =177.47×10-3Kg;上海地区的重力加速度g=9.794m/s2;张力
=177.47×10-3Kg;上海地区的重力加速度g=9.794m/s2;张力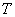 =177.47×10-3×9.794=1.738N,实验结果如表2所示:
=177.47×10-3×9.794=1.738N,实验结果如表2所示:
表2给定张力的实验数据表


图4 波长对数-频率对数关系图
经最小二乘法拟合得log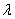 -log
-log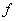 的斜率为:-0.9948,相关系数为:0.99。
的斜率为:-0.9948,相关系数为:0.99。
实验结果得到log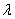 -log
-log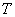 的斜率接近0.5;log
的斜率接近0.5;log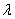 -log
-log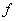 的斜率接近-1。验证了弦线上横波的传播规律,即横波的波长
的斜率接近-1。验证了弦线上横波的传播规律,即横波的波长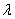 与弦线张力T的平方根成正比,与波源的振动频率
与弦线张力T的平方根成正比,与波源的振动频率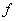 成反比。
成反比。
【注意事项】
1、须在弦线上出现振幅较大而稳定的驻波时,再测量驻波波长。
2、张力包括砝码与砝码盘的质量,砝码盘的质量用分析天平称量。
3、当实验时,发现波源发生机械共振时,应减小振幅或改变波源频率,便于调节出振幅大且稳定的驻波。
【思考题】
1、求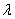 时为何要测几个半波长的总长?
时为何要测几个半波长的总长?
2、为了使log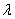 -log
-log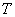 直线图上的数据点分布比较均匀,砝码盘中的砝码质量应如何改变?
直线图上的数据点分布比较均匀,砝码盘中的砝码质量应如何改变?
3、为何波源的簧片振动频率尽可能避开振动源的机械共振频率?
4、弦线的粗细和弹性对实验各有什么影响,应如何选择?
第二篇:弦线振动法测定液体密度实验27
《弦线振动法测定液体密度实验》实验提要
实验课题及任务
《弦线振动法测定液体密度实验》实验课题任务是:研究弦线振动时波长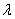 的大小与弦线受到的张力
的大小与弦线受到的张力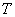 有关,在其它条件不变的情况,改变弦线受到的张力即可改变波长
有关,在其它条件不变的情况,改变弦线受到的张力即可改变波长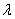 ,通过比较同一砝码在空气中与在待测液体中时分别产生的张力不同,而产生不同的波长
,通过比较同一砝码在空气中与在待测液体中时分别产生的张力不同,而产生不同的波长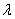 ,进一步求出待测液体的密度。
,进一步求出待测液体的密度。
学生根据自己所学的知识,并在图书馆或互联网上查找资料,设计出《物体在液体中的运动研究》的整体方案,内容包括:写出实验原理和理论计算公式,研究测量方法,写出实验内容和步骤,然后根据自己设计的方案,进行实验操作,记录数据,做好数据处理,得出实验结果,写出完整的实验报告,也可按书写科学论文的格式书写实验报告。
设计要求
⑴ 通过查找资料,并到实验室了解所用仪器的实物以及阅读仪器使用说明书,了解仪器的使用方法,找出所要测量的物理量,并推导出计算公式,在此基础上写出该实验的实验原理。
⑵ 选择实验的测量仪器,画出实验装置原理图,设计出实验方法和实验步骤,要具有可操作性。
⑶ 写出浸入待测液体中的物体体积的测量可行方法;
⑷ 写出浸入待测液体的密度公式,并计算出待测液体的密度 。
。
⑸ 分析讨论实验结果。
实验仪器
弦振动实验仪一套、水、待测液体、烧杯等。
实验提示
物体浸没在液体中受到的浮力大小为:
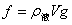
弦线在振动时频率 、波长
、波长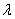 、张力
、张力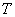 及弦线的线密度
及弦线的线密度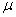 有如下关系:
有如下关系:
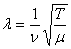
当频率 与线密度
与线密度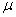 一定时,上式左右两边同时取对数,得到下式后还可以进一步简化。
一定时,上式左右两边同时取对数,得到下式后还可以进一步简化。


弦振动法测定液体密度
实验目的
1.弦振动实验仪的使用,以及巩固物理天平的使用。
2. 研究弦线振动波长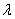 的大小与弦线受到的张力
的大小与弦线受到的张力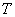 的关系.
的关系.
3.掌握浸入待测液体中的物体体积的测量可行方法
4.学会用最小二乘法进行线性拟合,计算待测液体的密度
实验仪器
弦振动实验仪一套、物理天平、米尺弦线、细线、烧杯。
实验原理
研究弦线振动时波长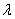 的大小与弦线受到的张力
的大小与弦线受到的张力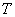 有关,在
有关,在
它条件不变的情况,改变弦线受到的张力即可改变波长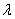 ,通过
,通过
较同一砝码在空气中与在待测液体中时分别产生的张力不同,而
产生不同的波长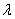 ,进一步求出待遇测液体的密度。
,进一步求出待遇测液体的密度。
1. 弦线在振动时频率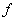 (调节音叉的频率
(调节音叉的频率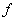 =100Hz)共振时,弦线出现稳定的强烈振动,驻波的振幅最大,此时的弦振动频率应当和相同,所以频率
=100Hz)共振时,弦线出现稳定的强烈振动,驻波的振幅最大,此时的弦振动频率应当和相同,所以频率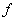 =100Hz
=100Hz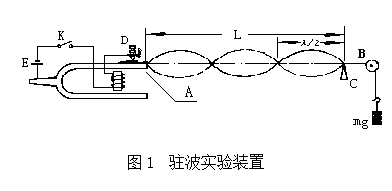
2.波长的测定实验装置如图1所示,将弦线的一端固定在电动音叉的一个叉子的顶端,另一端绕过滑轮系在载有砝码的砝码盘上。闭合K后,调节音叉断续器的接触点螺丝D,使音叉维持稳定的振动,并将其振动沿弦线向滑轮一端传播,形成横波。当横波到达B点后产生反射,由于前进波与反射波能够满足相干条件,在弦线上形成驻波,而任意两个相邻的波节(或波腹)间的距离都为波长的一半。若调节弦线的长度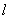 ,使驻波振幅最大且稳定,则波长为
,使驻波振幅最大且稳定,则波长为
 , n为半波数 (1)
, n为半波数 (1)
同样有当物体在液体中时弦线振动的波长为
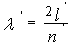 (2)
(2)
其中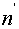 为在液体中时的半波数,
为在液体中时的半波数,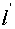 为此时的弦线长。
为此时的弦线长。
3.张力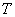 的测定
的测定
弦线在振动时频率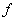 、波长
、波长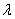 、张力
、张力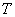 及弦线的线密度
及弦线的线密度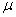 有如下关系:
有如下关系:
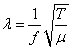
则  (3)
(3)
此即物体在空气中时,测得的的弦线受到的张力。
同理:当物体在液体中时,测得波长为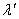 ,则同一砝码在空气中弦线受到的张力
,则同一砝码在空气中弦线受到的张力
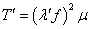 (4)
(4)
4.测量物体的体积
阿几米德原理指出:浸没在液体中的物体受到向上的浮力,其大小等于物体所排开液体的重量。根据这个定律,我们可以求出物体的体积。先将质量为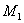 的物体用细线扎好,挂在天平挂钩上,将物体浸入水中,然后用天平进行秤衡. 天平秤衡时,砝码的重量
的物体用细线扎好,挂在天平挂钩上,将物体浸入水中,然后用天平进行秤衡. 天平秤衡时,砝码的重量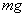 就是线的张力。如图(2)所示
就是线的张力。如图(2)所示
由物体此时处于平衡,所以有:
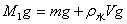
则  (5)
(5)
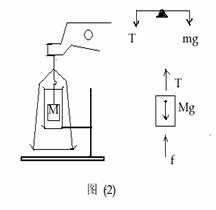
5.物体浸没在液体中受到的浮力大小为:
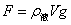 (6)
(6)
在空气中时:物体受到张力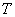 =
=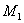 g,在浸没液体时,物体受到的张力
g,在浸没液体时,物体受到的张力 ,和浮力
,和浮力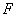 的作用下平衡,可得
的作用下平衡,可得
 (7)
(7)
6.综合以上各式,有
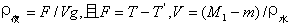
即 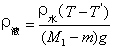 (8)
(8)
又因为 =
=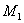 g,
g, 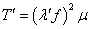
即 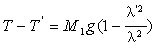 (9)
(9)
将(9)式代入(8)式中,得
液体的密度 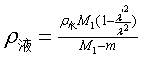 (10)
(10)
由(10)式可知,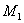 ,m分别为测量物体在空气中和浸没液体中的质量,可通过直接物理测量求得;λ,
,m分别为测量物体在空气中和浸没液体中的质量,可通过直接物理测量求得;λ,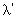 可通过测量出半波数n及弦线长l,再根据
可通过测量出半波数n及弦线长l,再根据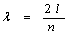 求的;
求的;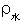 可先测得水中温度t,,再查表得到。
可先测得水中温度t,,再查表得到。
实验内容及步骤:
1. 调节弦线在振动时频率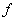 =100Hz
=100Hz
调节音叉的频率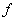 0=100Hz。共振时,弦线出现稳定的强烈振动,驻波的振幅最大,此时的弦振动频率应当和音叉的频率
0=100Hz。共振时,弦线出现稳定的强烈振动,驻波的振幅最大,此时的弦振动频率应当和音叉的频率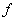 0相同,所以弦线在振动时频率
0相同,所以弦线在振动时频率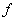 =100Hz。
=100Hz。
因此,每次测量波长时必须使弦线出现稳定的强烈振动,且驻波的振幅最大。
2.波长的测定
空气中:如图(1)所示,连接好电路,将物体县挂在线的一端。打开电源后,适当调节弦长(音叉端到滑轮轴间的线长),在弦上将出现稳定的强烈地振动,且驻波的振幅最大,即弦与音叉共振。记下弦上的半波数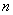 ,线长
,线长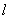 。测量完一组数据后加一个砝码再测,依次类推,测量5组数据。
。测量完一组数据后加一个砝码再测,依次类推,测量5组数据。
液体中:将物体浸没在液体中,适当调节弦长,使弦上出现稳定的强烈地振动。记下弦上的半波数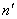 ,线长
,线长 。测量完一组数据后加一个砝码再测,依次类推,测量5组数据。
。测量完一组数据后加一个砝码再测,依次类推,测量5组数据。
3.测量物体在空气中的质量m
按照物理天平测量物体质量的方法,在原有的砝码盘上加上一个砝码测其质量,测量完一组数据后加一个砝码再测,依次类推,测量5组数据。
4. 测量物体在水中的质量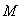
先将细铜线连接好砝码盘,挂在天平挂钩上,加上一个砝码,使其浸入水中,然后用天平进行秤衡. 测量完一组数据后加一个砝码再测,依次类推,测量5组数据。
5.用温度计测量烧杯中水的温度t,记录数据,再根据其温度值查找出该温度下的水的密度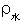 。
。
6.计算出该液体的密度及相对不确定度。
实验数据:
频率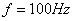 g=9.8
g=9.8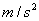
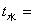 23.0
23.0 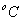
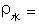 0.9976×103kg/m3
0.9976×103kg/m3
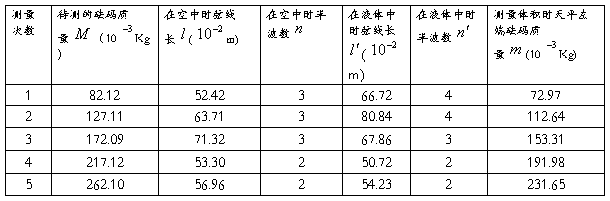
数据处理:

由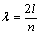 ,计算各个密度的值(填入表格):
,计算各个密度的值(填入表格):
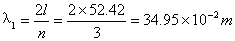

同理可得:
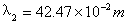



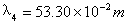
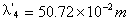
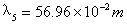
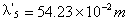
根据(10)式可知:
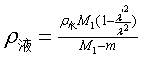
∴
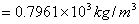
同理可得:
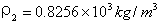
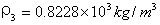
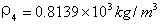

∴
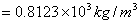
由于每组数据都是独立的,且每次测量都是单次的,因此
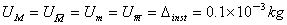
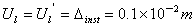
又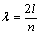 ,得
,得

∴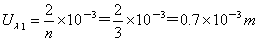
同理: 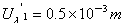
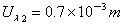


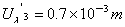
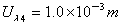
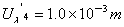

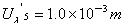
∴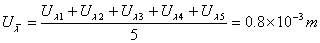
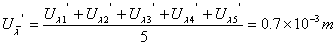
又由于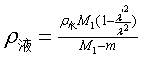 ,有
,有
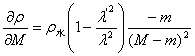
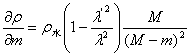
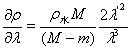
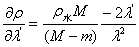
即


同理:
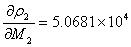
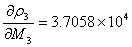
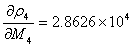

即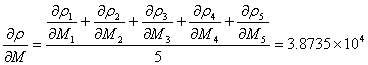
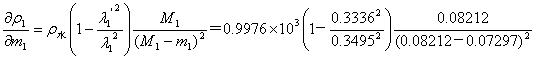
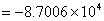
同理:
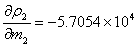
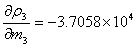
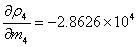
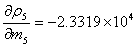
即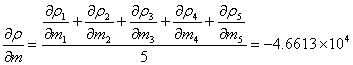

同理:
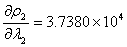
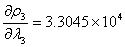
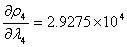

即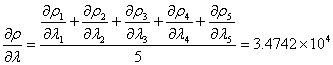
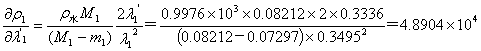
同理:
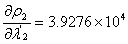
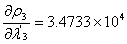
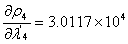
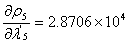
即
又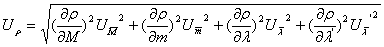
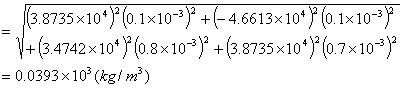
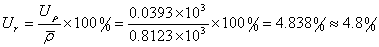
实验结果表达
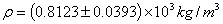
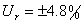
分析讨论实验结果
本实验测得的液体密度是间接测量量,通过与直接测量量的相关公式求得,其不确定度是利用标准偏差传递公式进行估算求得。从实验结果来看,相对不确定度还是有点偏大。其原因是仪器误差和个人操作误差所引起的(如不能准确判断何时弦线出现稳定的强烈振动,且驻波的振幅最大及弦线共振点的确定等等)。我们可以通过下列方法减少误差,降低相对不确定度:
1.测量波长时,调节弦线出现稳定的强烈振动,且驻波的振幅最大,同时尽量使弦上的半波数多点。
2.测量水中物体质量时,使砝码盘(包含吊钩)及砝码完全浸入水中,防止吊钩时在水中,时在空中而产生的误差。
心得体会:
通过这个实验,学会了测定液体的密度的另一种方法,同时也掌握了通过测量物体在空气中和液体中不同质量,通过一系列计算得出物体的体积。在利用标准偏差传递公式进行估算求液体密度不确定度时,更是让我明白高等数学知识对物理试验数据处理的重要性。更重要的时,锻炼了独自动手能力及思维能力,了解自己的不足之处,加以重视。
-
实验报告样本- 弦线上驻波
实验题目横波在弦线上的传播规律一实验目的1观察弦线上形成的驻波用实验验证在频率一定时驻波波长与张力的关系2在张力不变时验证驻波波长…
-
弦线上的驻波实验
实验一弦线上的驻波实验在自然现象中振动现象广泛地存在着振动在媒质中传播就形成波波的传播有两种形式纵波和横波驻波是一种波的干涉比如乐…
-
实验3弦线上驻波实验
实验3弦线上驻波实验一实验目的1观察在弦上形成的驻波并用实验确定弦线振动时驻波波长与张力的关系2在弦线张力不变时用实验确定弦线振动…
-
实验 弦线上的驻波实验指导书
实验目的1观察弦振动及驻波的形成3在振动源频率不变时用实验确定驻波波长与张力的关系4在弦线张力不变时用实验确定驻波波长与振动频率的…
-
实验五 研究弦线上的驻波现象
实验五研究弦线上的驻波现象一实验目的1观察弦线上驻波的变化了解并熟悉实验仪器的调整方法2研究弦线振动时的振动频率与振幅变化对形成驻…
-
实验报告样本- 弦线上驻波
实验题目横波在弦线上的传播规律一实验目的1观察弦线上形成的驻波用实验验证在频率一定时驻波波长与张力的关系2在张力不变时验证驻波波长…
-
弦线上的驻波实验
实验一弦线上的驻波实验在自然现象中振动现象广泛地存在着振动在媒质中传播就形成波波的传播有两种形式纵波和横波驻波是一种波的干涉比如乐…
-
实验 弦线上的驻波实验指导书
实验目的1观察弦振动及驻波的形成3在振动源频率不变时用实验确定驻波波长与张力的关系4在弦线张力不变时用实验确定驻波波长与振动频率的…
-
实验五 研究弦线上的驻波现象
实验五研究弦线上的驻波现象一实验目的1观察弦线上驻波的变化了解并熟悉实验仪器的调整方法2研究弦线振动时的振动频率与振幅变化对形成驻…
-
线上的驻波实验
实验弦线上的驻波实验引言弦线上波的传播规律的研究是力学中的重要内容本实验重点在于观测弦线上形成的驻波并用实验确定弦振动时驻波波长与…
-
实验6 弦线上的驻波
实验6弦线上的驻波实验目的1了解弦线上的驻波2通过弦线振动测定弦振动的频率3测量弦线上横波的传播速度实验仪器XZDYB型固定均匀弦…