系统仿真实验报告

班级：电气工程及其自动化1301班

学号：

姓名：

指导老师：

完成时间：20##年4月19日

实验一 MATLAB中矩阵与多项式的基本运算.................................................................. - 1 -

实验二 MATLAB绘图命令....................................................................................................... 8

实验三 MATLAB程序设计..................................................................................................... 10

实验四 MATLAB的符号计算与SIMULINK的使用........................................................... 11

实验五 MATLAB在控制系统分析中的应用......................................................................... 13

实验六连续系统数字仿真的基本算法.................................................................................. 22

实验一 MATLAB中矩阵与多项式的基本运算

实验任务

1．了解MATLAB命令窗口和程序文件的调用。

2．熟悉如下MATLAB的基本运算：

① 矩阵的产生、数据的输入、相关元素的显示；

② 矩阵的加法、乘法、左除、右除；

③ 特殊矩阵：单位矩阵、“1”矩阵、“0”矩阵、对角阵、随机矩阵的产生和运算；

④ 多项式的运算：多项式求根、多项式之间的乘除。

【命令】与【运行结果】

>> eye(3)

ans =

1 0 0

0 1 0

0 0 1

>> ones(3)

ans =

1 1 1

>> zeros(3,4)

ans =

0 0 0 0

>> rand(3,4)

ans =

0.8147 0.9134 0.2785 0.9649

0.9058 0.6324 0.5469 0.1576

0.1270 0.0975 0.9575 0.9706

>> diag(3)

ans =

>> A=rand(3),diag(A)

A =

0.9572 0.1419 0.7922

0.4854 0.4218 0.9595

0.8003 0.9157 0.6557

ans =

0.9572

0.4218

0.6557

>> A=[1 2 3;4 5 6;7 8 9];...

B=[1 3 5;7 9 2;4 6 8];...

A＼B,B/A,inv(A)*B ,B*inv(A),inv(B)*A

Warning: Matrix is close to singular or badly scaled.

Results may be inaccurate. RCOND = 1.541976e-018.

ans =

1.0e+016 *

4.0532 4.0532 -4.0532

-8.1065 -8.1065 8.1065

4.0532 4.0532 -4.0532

Warning: Matrix is singular to working precision.

ans =

NaN -Inf Inf

Warning: Matrix is close to singular or badly scaled.

Results may be inaccurate. RCOND = 1.541976e-018.

ans =

1.0e+016 *

4.0532 4.0532 -4.0532

-8.1065 -8.1065 8.1065

4.0532 4.0532 -4.0532

Warning: Matrix is close to singular or badly scaled.

Results may be inaccurate. RCOND = 1.541976e-018.

ans =

1.0e+016 *

0.0000 0 0

4.0532 -8.1065 4.0532

0 0 0

ans =

3.5000 3.0000 2.5000

-2.5000 -2.0000 -1.5000

1.0000 1.0000 1.0000

【结果分析】

题目中的矩阵A是没有逆的，但由于计算机精度的问题，使得上面的结果比较奇怪：

首先，B/A应该和B*inv（A）都出错显示结果为无定义，但是事实上却是前者结果无定义，而后者却又结果。另外A\B和inv(A)*B 应该也是没有定义的，但还是有结果，因此，我们有必要检查运算结果，鉴于软件在精度方面不可避免的误差。

>>syms x

f=3*x^5+4*x^3-5*x^2-7*x+5;

p=[3,0,4,-5,-7,5];

X=roots(p)

poly(X)

X =

-0.3074 + 1.6176i

-0.3074 - 1.6176i

-1.0000

1.0000

0.6147

ans =

1.0000 0.0000 1.3333 -1.6667 -2.3333 1.6667

>> A=fix(10*rand(1,3)),B=fix(20*rand(1,4))

conv(A,B)，[Q,r]=deconv(B,A)

A =

6 1 1

B =

9 19 6 11

ans =

54 123 64 91 17 11

Q =

1.5000 2.9167

r =

0 0 1.5833 8.0833

>> A=fix(10*rand(3)),B=fix(20*rand(3))

A*B，A.*B

A =

2 3 5

6 8 9

4 5 2

B =

15 11 10

15 1 15

7 1 18

ans =

110 30 155

273 83 342

149 51 151

ans =

30 33 50

90 8 135

28 5 36

【结果分析】：A*B是正常的规矩乘法，而A.*B是一种扩展功能，其结果C_ij=A_ij*B_ij_。

>> who

Your variables are:

A B Q X ans f p r x

>> whos

Name Size Bytes Class Attributes

A 3x3 72 double

B 3x3 72 double

Q 1x2 16 double

X 5x1 80 double complex

ans 3x3 72 double

f 1x1 170 sym

p 1x6 48 double

r 1x4 32 double

x 1x1 126 sym

>> A=fix(10*rand(1,3)),B=fix(20*rand(3)),C=fix(10*rand(3,2)),D=[3]

diag(A),diag(B),diag(C),diag(D)

A =

8 0 3

B =

5 18 2

16 3 2

8 5 17

C =

5 8

5 6

1 3

D =

ans =

8 0 0

0 0 0

0 0 3

ans =

>> disp('lalalalaalalllallla');

A=fix(10*rand(3,2)),B=zeros(3),C=ones(3,6)

size(A),length(A),size(B),length(B),size(C),length(C)

lalalalaalalllallla

A =

2 9

4 9

0 4

B =

0 0 0

C =

1 1 1 1 1 1

ans =3 2

ans =3

ans =3 3

ans =3

ans =3 6

ans =6

【结果分析】：disp不受”;分号”影响，size输出矩阵的行数和列数，length输出行列数较大值

实验二 MATLAB绘图命令

实验任务

熟悉MATLAB基本绘图命令，掌握如下绘图方法：

1．坐标系的选择、图形的绘制；

2．图形注解（题目、标号、说明、分格线）的加入；

3．图形线型、符号、颜色的选取。

【程序】

x=linspace(0,100,pi);

y1=x.*x;

y2=x.*x.*x;

subplot(2,2,1);plot(x,y1,'-.b',x,y2,'r'),legend('y=x^{2}','y=x^{3}');　grid off;

subplot(2,2,2);loglog(x,y1,'rp-',x,y2,':b'),title('说啥好呢'),grid on;

subplot(2,2,3);semilogx(x,y1,'b*-',x,y2,'r+-'),xlabel('X'),ylabel('Y');

subplot(2,2,4);semilogy(x,y1,'g-+',x,y2,'m'),text(50,8000,'y=x^{2}'),

text(40,100000,'y=x^{3}')

【结果截图】

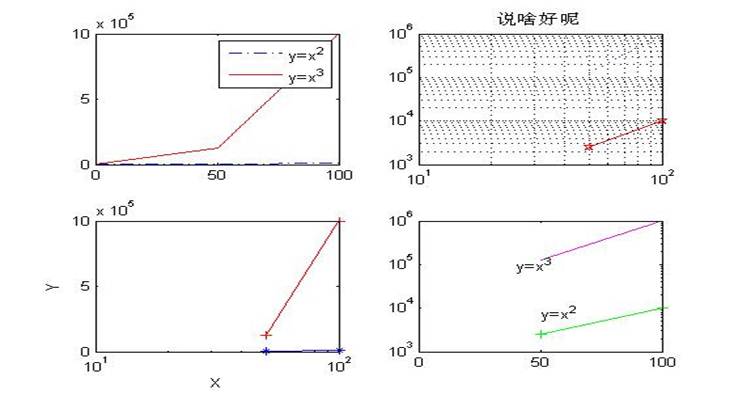【程序】

t=0:0.01:2*pi;

r=sin(2*t).*cos(2*t);

subplot(2,2,1);polar(t,r)

subplot(2,2,2);bar(t,r,'r'),axis([0,1,-0.5,0.5]),title('bar')

subplot(2,1,2);stairs(t,r,'c'),axis([0,1,-0.5,0.5]),title('stairs')

【结果截图】

【程序】

[x,y,z]=peaks(100);

subplot(1,2,1),mesh(x,y,z)

subplot(1,2,2),contour(x,y,z)

【结果截图】

实验三 MATLAB程序设计

实验任务

用一个MATLAB语言编写一个程序：输入一个自然数，判断它是否是素数，如果是，输出“It is one prime”，如果不是，输出“It is not one prime.”。要求通过调用子函数实现。最好能具有如下功能：①设计较好的人机对话界面，程序中含有提示性的输入输出语句。②能实现循环操作，由操作者输入相关命令来控制是否继续进行素数的判断。如果操作者希望停止这种判断，则可以退出程序。③如果所输入的自然数是一个合数，除了给出其不是素数的结论外，还应给出至少一种其因数分解形式。例：输入 6，因为6不是素数。则程序中除了有“It is not one prime”的结论外，还应有：“6=2*3”的说明。

【程序】：

a=input('请输入一个整数(end in 0):');

while(a~=0)

if a==1

disp('1 is not a prime or a composite number.')

elseif isprime(a)==1

fprintf('%d is a prime.\n',a)

elseif isprime(a)==0

f=factor(a);m=length(f);

fprintf('%d is not a prime,%d=%d',a,a,f(1))

for i=2:m

fprintf('*%d',f(i));

end

fprintf('\n');

end

a=input('请输入一个整数(end in 0):');

end

【运行结果】：

请输入一个整数(end in 0):1

1 is not a prime or a composite number.

请输入一个整数(end in 0):2

2 is a prime.

请输入一个整数(end in 0):35

35 is not a prime,35=5*7

请输入一个整数(end in 0):0

实验四 MATLAB的符号计算与SIMULINK的使用

实验任务

1．掌握MATLAB符号计算的特点和常用基本命令；

2．掌握SIMULINK的使用。

【程序1】

syms a b c d

A=[a b;c d];B=[1,4;2,9]; det(A),det(B),eig(A),eig(B)

【运行结果1】

ans = a*d-b*c

ans = 1

ans = 1/2*a+1/2*d+1/2*(a^2-2*a*d+d^2+4*b*c)^(1/2)

1/2*a+1/2*d-1/2*(a^2-2*a*d+d^2+4*b*c)^(1/2)

ans = 0.1010

9.8990

【程序2】

r=solve('x^3+5*x^2-9*x+17')

r4=vpa(r,4)

r10=vpa(r,10)

【运行结果2】

r =

-1/3*(557+3*18849^(1/2))^(1/3)-52/3/(557+3*18849^(1/2))^(1/3)-5/3

1/6*(557+3*18849^(1/2))^(1/3)+26/3/(557+3*18849^(1/2))^(1/3)-5/3+1/2*i*3^(1/2)*(-1/3*(557+3*18849^(1/2))^(1/3)+52/3/(557+3*18849^(1/2))^(1/3))

1/6*(557+3*18849^(1/2))^(1/3)+26/3/(557+3*18849^(1/2))^(1/3)-5/3-1/2*i*3^(1/2)*(-1/3*(557+3*18849^(1/2))^(1/3)+52/3/(557+3*18849^(1/2))^(1/3))

r4 =

-6.717

.858-1.339*i

.858+1.339*i

r10 =

-6.716750613

.858375306-1.339469138*i

.858375306+1.339469138*i

【simulink仿真】

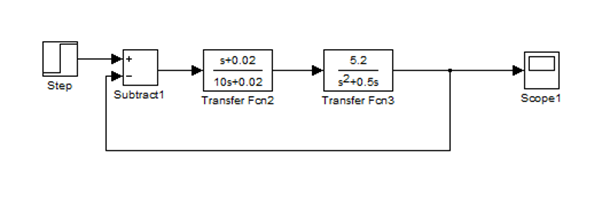【仿真结果】

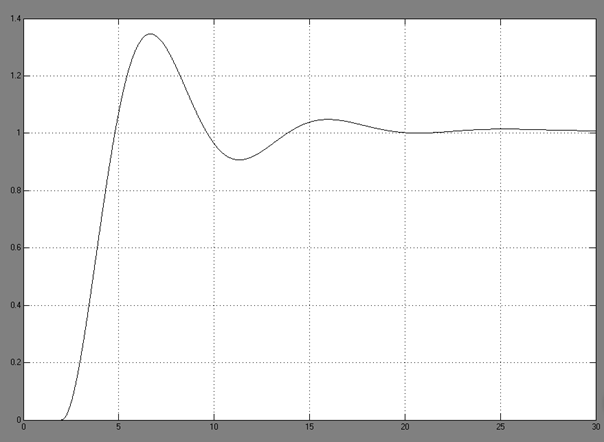
实验五 MATLAB在控制系统分析中的应用

一、实验任务

1．掌握MATLAB在控制系统时间响应分析中的应用；

2．掌握MATLAB在系统根轨迹分析中的应用；

3. 掌握MATLAB控制系统频率分析中的应用；

4. 掌握MATLAB在控制系统稳定性分析中的应用

1. 求下面系统的单位阶跃响应

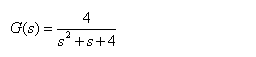
【程序】

num=[4] ; den=[1 , 1 , 4] ;step(num , den)

[y , x , t]=step(num , den) ;

tp=spline(y , t , max(y)) %计算峰值时间

ymaxmax(y) %计算峰值

【结果】

tp =1.5708

ymax =1.4419

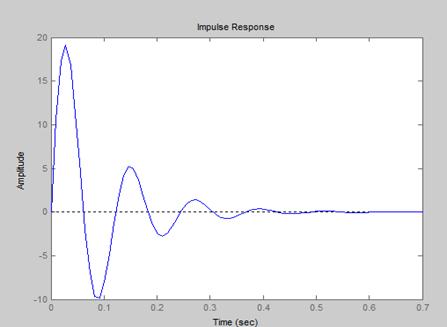
2. 求下面系统的单位脉冲响应：

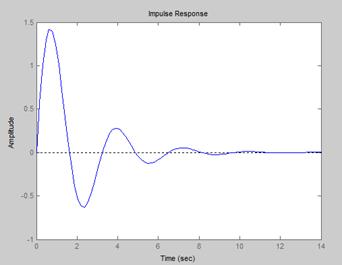
【程序】

num=[4] ; den=[1 , 1 ,4] ;

impulse(num,den)

【结果如右图】

3.已知二阶系统的状态方程为：

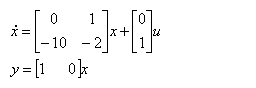
求系统的零输入响应和脉冲响应。

【程序如下】：【结果如下图】

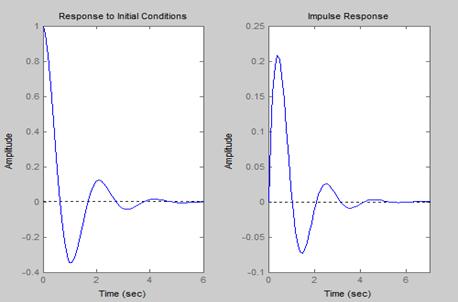a=[0 , 1 ; -10 , -2] ;

b=[0 ; 1] ;

c=[1 , 0] ;

d=[0] ;

x0=[1 ,0];

subplot(1 , 2 , 1) ;

initial(a , b , c ,d,x0)

subplot(1 , 2 , 2) ;

impulse(a , b , c , d)

4.系统传递函数为：

输入正弦信号时，观察输出信号的相位差。

【程序如下】：【结果如下图】：

num=[1] ; den=[1 , 1] ;

t=0 : 0.01 : 10 ;

u=sin(2*t) ;

hold on

plot(t , u , ‘r’)

lsim(num , den , u , t)

5.有一二阶系统，求出周期为4秒的方波的输出响应

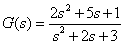
【程序如下】：【结果如下图】：

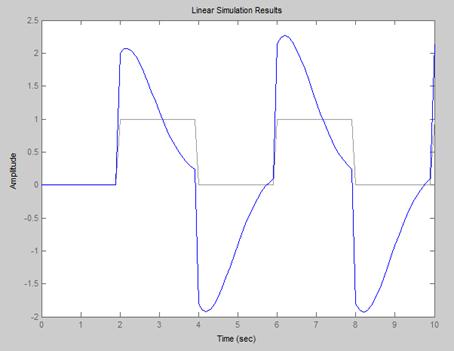num=[2 5 1];

den=[1 2 3];

t=(0:.1:10);

period=4;

u=(rem(t,period)>=period./2);

lsim(num,den,u,t);

6.已知开环系统传递函数，绘制系统的根轨迹，并分析其稳定性

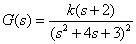
【程序如下】：

num=[1 2];den1=[1 4 3];den=conv(den1,den1);figure(1)

rlocus(num,den)

[k,p]= rlocfind(num,den)

figure(2)

k=55;num1=k*[1 2];den=[1 4 3];den1=conv(den,den);[num,den]=cloop(num1,den1,-1);

impulse(num,den)

title('impulse response (k=55) ')

figure(3)

k=56;num1=k*[1 2];den=[1 4 3];den1=conv(den,den);[num,den]=cloop(num1,den1,-1);

impulse(num,den)

title('impulse response(k=56)')

【结果】：

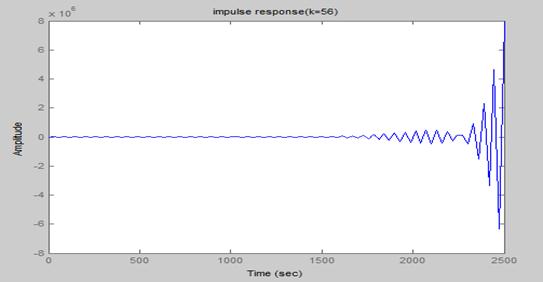
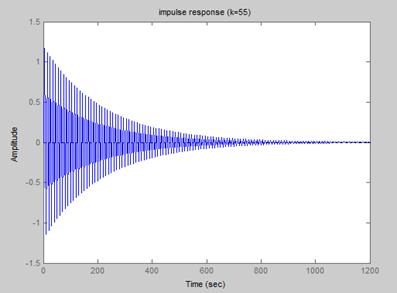
K=55时系统稳定，k=56时系统发散。

7. 作如下系统的bode图

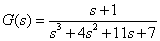
【程序如下】：【结果】：

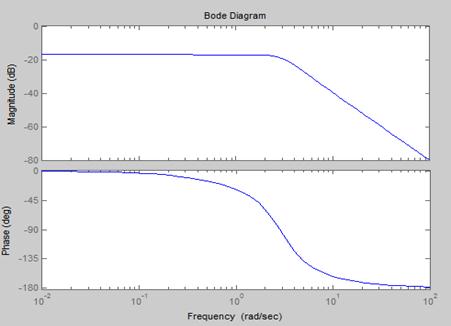n=[1 , 1] ;

d=[1 , 4 , 11 , 7] ;

bode(n , d)

8.系统传函如下

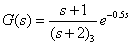
求有理传函的频率响应，然后在同一张图上绘出以四阶伯德近似表示的系统频率响应

【程序如下】：

num=[1];den=conv([1 2],conv([1 2],[1 2]));

w=logspace(-1,2); t=0.5;

[m1,p1]=bode(num,den,2);

p1=p1-t*w'*180/pi; [n2,d2]=pade(t,4);

numt=conv(n2,num);dent=(conv(den,d2));

[m2,p2]=bode(numt,dent,w);

subplot(2,1,1);

semilogx(w,20*log10(m1),w,20*log10(m2),'k--');

title('bode plot');xlabel('frequency');ylabel('gain');

subplot(2,1,2);

semilogx(w,p1,w,p2,'k--');

xlabel('frequency');ylabel('phase');

【结果如下图】：

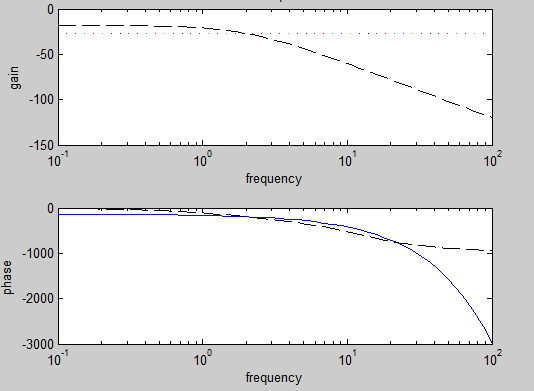
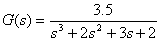9.已知系统模型为

求它的幅值裕度和相角裕度

【程序如下】：

n=[3.5]; d=[1 2 3 2];

[Gm,Pm,Wcg,Wcp]=margin(n,d)

【结果】：

Gm =1.1433

Pm =7.1688

Wcg =1.7323

Wcp =1.6541

10.二阶系统为：

令wn=1,分别作出ξ=2 , 1 , 0.707 , 0.5时的nyquist曲线。

【程序如下】：

n=[1] ;

d1=[1 , 4 , 1] ; d2=[1 , 2 , 1] ; d3=[1 , 1.414 , 1]; d4=[1,1,1];

nyquist(n,d1) ;

hold on

nyquist(n,d2) ; nyquist(n,d3) ; nyquist(n,d4) ;

【结果如下图】：

11.一多环系统，其结构图如下，使用Nyquist频率曲线判断系统的稳定性。

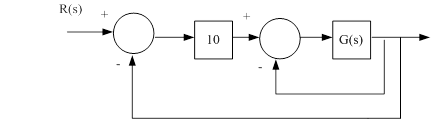
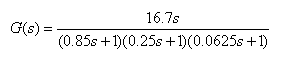
【程序如下】：

k1=16.7/0.0125;z1=[0]; p1=[-1.25 -4 -16]; [num1,den1]=zp2tf(z1,p1,k1);
[num,den]=cloop(num1,den1); [z,p,k]=tf2zp(num,den);
figure(1)
nyquist(num,den)
figure(2)
[num2,den2]=cloop(num,den); impulse(num2,den2);

【结果如下图】：

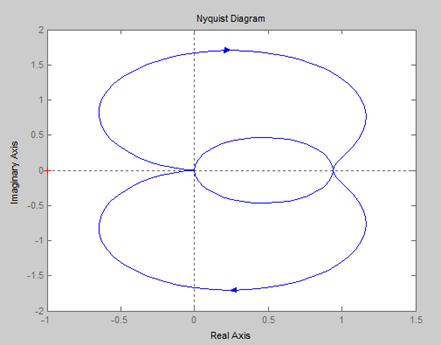
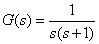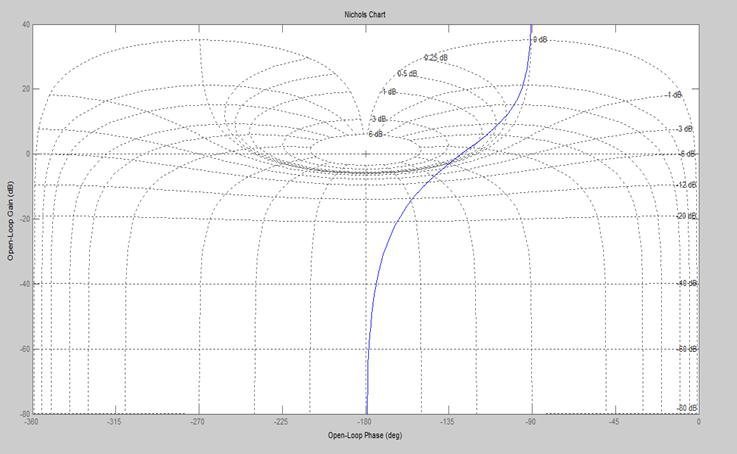
12. 已知系统为：

作该系统的nichols曲线。

【程序如下】：

n=[1] ; d=[1 , 1 , 0] ; ngrid(‘new’) ; nichols(n , d) ;

【结果如下图】：

实验六连续系统数字仿真的基本算法

实验任务

1．理解欧拉法和龙格-库塔法的基本思想；

2．理解数值积分算法的计算精度、速度、稳定性与步长的关系；

1. 取h=0.2，试分别用欧拉法、RK2法和RK4法求解微分方程的数值解，并比较计算精度。

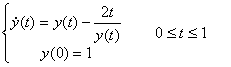
注：解析解：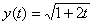

【程序】

clear

t(1)=0; % 置自变量初值

y(1)=1; y_euler(1)=1; y_rk2(1)=1; y_rk4(1)=1; % 置解析解和数值解的初值

h=0.2; % 步长

% 求解析解

for k=1:5

t(k+1)=t(k)+h;

y(k+1)=sqrt(1+2*t(k+1));

end

% 利用欧拉法求解

for k=1:5

y_euler(k+1)=y_euler(k)+h*(y_euler(k)-2*t(k)/y_euler(k));

end

% 利用RK2法求解

for k=1:5

k1=y_rk2(k)-2*t(k)/y_rk2(k);

k2=(y_rk2(k)+h*k1)-2*(t(k)+h)/(y_rk2(k)+h*k1);

y_rk2(k+1)=y_rk2(k)+h*(k1+k2)/2;

end

% 利用RK4法求解

for k=1:5

k1=y_rk4(k)-2*t(k)/y_rk4(k);

k2=(y_rk4(k)+h*k1/2)-2*(t(k)+h/2)/(y_rk4(k)+h*k1/2);

k3=(y_rk4(k)+h*k2/2)-2*(t(k)+h/2)/(y_rk4(k)+h*k2/2);

k4=(y_rk4(k)+h*k3)-2*(t(k)+h)/(y_rk4(k)+h*k3);

y_rk4(k+1)=y_rk4(k)+h*(k1+2*k2+2*k3+k4)/6;

end

disp(' 时间解析解欧拉法 RK2法 RK4法')

yt=[t', y', y_euler', y_rk2', y_rk4'];

disp(yt)

【运行结果】

时间解析解欧拉法 RK2法 RK4法

0 1.0000 1.0000 1.0000 1.0000

0.2000 1.1832 1.2000 1.1867 1.1832

0.4000 1.3416 1.3733 1.3483 1.3417

0.6000 1.4832 1.5315 1.4937 1.4833

0.8000 1.6125 1.6811 1.6279 1.6125

1.0000 1.7321 1.8269 1.7542 1.7321

%H=0.05

时间解析解欧拉法 RK2法 RK4法

0 1.0000 1.0000 1.0000 1.0000

0.0500 1.0488 1.0500 1.0489 1.0488

0.1000 1.0954 1.0977 1.0956 1.0954

0.1500 1.1402 1.1435 1.1403 1.1402

0.2000 1.1832 1.1876 1.1834 1.1832

0.2500 1.2247 1.2301 1.2250 1.2247

H=0.001

时间解析解欧拉法 RK2法 RK4法

0 1.0000 1.0000 1.0000 1.0000

0.0010 1.0010 1.0010 1.0010 1.0010

0.0020 1.0020 1.0020 1.0020 1.0020

0.0030 1.0030 1.0030 1.0030 1.0030

0.0040 1.0040 1.0040 1.0040 1.0040

0.0050 1.0050 1.0050 1.0050 1.0050

%欧拉法需要步长足够小时才逼近解析解，RK4逼近得最快，其次是RK2

2. 考虑如下二阶系统：

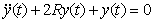在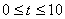上的数字仿真解（已知：，），

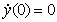并将不同步长下的仿真结果与解析解进行精度比较。

说明：

已知该微分方程的解析解分别为：

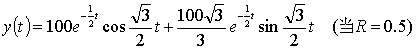
采用RK4法进行计算，选择状态变量：

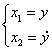
则有如下状态空间模型及初值条件

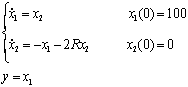
采用RK4法进行计算。程序如下：

clear

h=input('请输入步长h='); % 输入步长

M=round(10/h); % 置总计算步数

t(1)=0; % 置自变量初值

y_0(1)=100; y_05(1)=100; % 置解析解的初始值(y_0和y_05分别对应于为R=0和R=0.5)

x1(1)=100; x2(1)=0; % 置状态向量初值

y_rk4_0(1)=x1(1); y_rk4_05(1)=x1(1); % 置数值解的初值

% 求解析解

for k=1:M

t(k+1)=t(k)+h;

y_0(k+1)=100*cos(t(k+1));

y_05(k+1)=100*exp(-t(k+1)/2).*cos(sqrt(3)/2*t(k+1))+100*sqrt(3)/3*exp(-t(k+1)/2).*sin(sqrt(3)/2*t(k+1));

end

% 利用RK4法求解

% R=0

for k=1:M

k11=x2(k); k12=-x1(k);

k21=x2(k)+h*k12/2; k22=-(x1(k)+h*k11/2);

k31=x2(k)+h*k22/2; k32=-(x1(k)+h*k21/2);

k41=x2(k)+h*k32; k42=-(x1(k)+h*k31);

x1(k+1)=x1(k)+h*(k11+2*k21+2*k31+k41)/6;

x2(k+1)=x2(k)+h*(k12+2*k22+2*k32+k42)/6;

y_rk4_0(k+1)=x1(k+1);

end

% R=0.5

for k=1:M

k11=x2(k); k12=-x1(k)-x2(k);

k21=x2(k)+h*k12/2; k22=-(x1(k)+h*k11/2)-(x2(k)+h*k12/2);

k31=x2(k)+h*k22/2; k32=-(x1(k)+h*k21/2)-(x2(k)+h*k22/2);

k41=x2(k)+h*k32; k42=-(x1(k)+h*k31)-(x2(k)+h*k32);

x1(k+1)=x1(k)+h*(k11+2*k21+2*k31+k41)/6;

x2(k+1)=x2(k)+h*(k12+2*k22+2*k32+k42)/6;

y_rk4_05(k+1)=x1(k+1);

end

% 求出误差最大值

err_0=max(abs(y_0-y_rk4_0));

err_05=max(abs(y_05-y_rk4_05));

% 输出结果

disp('最大误差（R=0) 最大误差（R=0.5)')

err_max=[err_0,err_05];

disp(err_max)

步长h取0.0001 到0.5之间变化，并且将数值解直接与解析解比较，求出最大误差数据列入下表中。

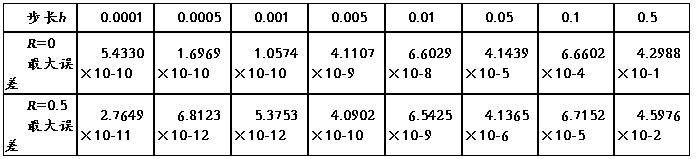
从上表中可以看出，当步长h=0.001时，总误差最小；当步长h小于0.001时，由于舍入误差变大而使总误差增加；当步长h大于0.001时，则由于截断误差的增加也使得总误差加大。另外，当系统的解变化激烈时（如R=0），误差对步长的变化较为敏感；当系统的解变化平稳时，步长的变化对误差的影响就要缓和得多。数值积分算法确定以后，在选择步长时，需要综合考虑。

相关推荐

系统仿真实验报告

实验一 MATLAB中矩阵与多项式的基本运算

实验二 MATLAB绘图命令

实验三 MATLAB程序设计

实验四 MATLAB的符号计算与SIMULINK的使用

实验五 MATLAB在控制系统分析中的应用

实验六 连续系统数字仿真的基本算法

专栏推荐

实验六连续系统数字仿真的基本算法