数学物理方程读书报告
数学物理方程读书报告
遥感与数字地球研究所 徐焕 201428007010031
数学物理方程这门课主要是为非数学专业理工科研究生的公共选修课,介绍偏微分方程的基本解法,变分法的基本思想和在求解常微偏微分方程中的应用, 提高学生解决实际问题的数学能力。通过学习我基本上在原本的基础上对于定解问题、行波法、分离变量法等基本掌握,对于基本解方法和变分法等问题有了初步的熟悉和运算。具体而言本课程具体内容总结如下:第一章 定解问题 基本概念;三类基本方程;定解问题:第二章 行波法 Duhamel原理;一维波动问题;空间波动方程:第三章 分离变量法 分离变量法的一般原则;本征值问题;曲线坐标系;特殊函数:第四章 基本解方法 热传导方程的基本解和初值问题;波动方程的基本解和初值问题;场位方程第一;边值问题的格林函数:第五章 变分法 泛函求导;泛函的极值问题;Euler-Lagrange 方程;Lagrange 乘子理论。现在具体分析每一章具体内容,着重分析泊松方程的格林函数法,内容如下:
第一章讲了数学模型的建立以及方程的定解条件和定解问题。在研究物理﹑力学和工程技术的过程中会遇到一些问题,要求反映物理模型的某种规律,这就需要建立起相应的数学模型,然后运用那个数学理论和方法求解这个数学模型,掌握有关物理量的变化规律。本章首先讲了偏微分方程的一般概念,并讨论了在偏微分方程理论中经常遇到的线性算子和对于线性偏微分方程的解成立的三个叠加原理。然后介绍了三大类二阶线性偏微分方程:双曲型方程、抛物型方程和椭圆型方程,它们的典型代表分别为:波动方程、热传导方程和拉普拉斯方程(泊松方程)。在介绍波动方程时,推导出了一维波动方程、m维波动方程及梁的横振动方程。从弦的横振动方程的推导过程可以知道,物体的振动产生了波的传播。热传导方程描述了热传导现象。拉普拉斯方程描述了电场中的势的分布规律。为了描述在特定条件下的物理状态的规律,不仅需要建立方程,还需要附加反映边界状态的边界条件以及与初始状态有关的初始条件。
第二章介绍了行波法和Duhamel原理。在求解常微分方程时,一般先求方程通解,通解含有任意常数,再利用初始条件确定这些常数。行波法就是仿照这个办法求解偏微分方程定解问题。先求偏微分方程的通解,而通解含有任意函数,再利用定解条件确定这些函数。行波法是求解无界域内定解问题的有效方法,但是只适用于很少的定解问题,如波动方程。
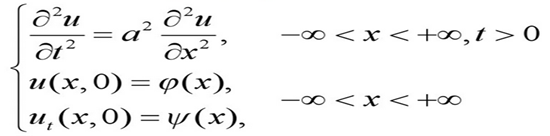
第三章介绍了求解偏微分方程最常见、最基本的方法—分离变量法。分离变量法的物理背景是波动现象,但是它不仅适用于波动方程,也适用于热传导方程、拉普拉斯方程以及某些形式更复杂的方程和方程组。分离变量法的基本思想是:利用变量分离形式的特解,将求解偏微分方程的定解问题化为求解常微分方程的问题,再利用定解条件和有关数学理论和方法求得定解问题的解。在利用分离变量法求解定解问题的过程中,都会涉及到求解特征值的问题。一个线性变换的一个特征向量(本征向量)是一个非退化向量,其方向在该变换下不变。该向量在该变换下缩放的比例称为其特征值(本征值)。
第四章介绍了基本解法。热传导方程的基本解和初值问题; 热传导问题和扩散问题满足热传导方程。热传导方程式(或称热方程)是一个重要的偏微分方程,它描述一个区域内的温度如何随时间变化。热传导在三维的等方向均匀介质里的传播可用方程式表达,其中u =u(t, x, y, z) 表温度,它是时间变量 t 与 空间变量 (x,y,z) 的函数。 /是空间中一点的温度对时间的变化率。 uxx, uyy 与 uzz 温度对三个空间坐标轴的二次导数。k决定于材料的热传导率、密度与热容。如果考虑的介质不是整个空间,则为了得到方程唯一解,必须指定 u 的边界条件。如果介质是整个空间,为了得到唯一性,必须假定解的增长速度有个指数型的上界,此假定吻合实验结果。格林函数,又称点源影响函数,是数学物理中的一个重要概念。格林函数代表一个点源在一定的边界条件和(或)初始条件下所产生的场。知道了点源的场,就可以用迭加的方法计算出任意源所产生的场。
一、 泊松方程的格林函数法
为了得到以格林函数表示的泊松方程解的积分表示式,需要用到格林公式,为此,我们首先介绍格林公式。
设u(r)和v(r)在区域 T 及其边界 S上具有连续一阶导数,而在 T 中具有连续二阶导数,应用矢量分析的高斯定理将曲面积分
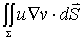
化成体积积分
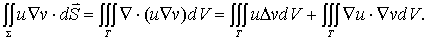 (12-1-1)
(12-1-1)
这叫作第一格林公式。同理,又有
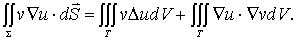 (12-1-2)
(12-1-2)
(12-1-1)与(12-1-2)两式相减,得

亦即
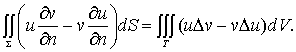 (12-1-3)
(12-1-3)
 表示沿边界S的外法向求导数。(12-1-3)叫作第二格林公式。
表示沿边界S的外法向求导数。(12-1-3)叫作第二格林公式。
现在讨论带有一定边界条件的泊松方程的求解问题。泊松方程是
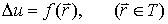 (12-1-4)
(12-1-4)
第一、第二、第三类边界条件可统一地表为
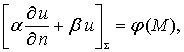 (12-1-5)
(12-1-5)
其中 j(M)是区域边界 S上的给定函数。a=0,b ≠0为第一类边界条件,a≠0,b=0是第二类边界条件,a、b 都不等于零是第三类边界条件。泊松方程与第一类边界条件构成的定解问题叫作第一边值问题或狄里希利问题,与第二类边界条件构成的定解问题叫作第二边值问题或诺依曼问题,与第三类边界条件构成的定解问题叫作第三边值问题。
为了研究点源所产生的场,需要找一个能表示点源密度分布的函数。§5.3中介绍的 d 函数正是描述一个单位正点量的密度分布函数。因此,若以v(r,r0)表示位于r0点的单位强度的正点源在r点产生的场,即v(r,r0)应满足方程
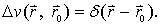 (12-1-6)
(12-1-6)
现在,我们利用格林公式导出泊松方程解的积分表示式。以v(r,r0)乘(12-1-4),u(r)乘(12-1-6),相减,然后在区域T中求积分,得
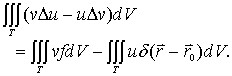 (12-1-7)
(12-1-7)
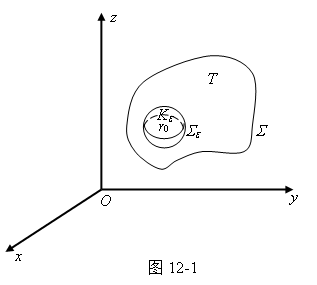
应用格林公式将上式左边的体积分化成面积分。但是,注意到在r=r0点,Dv具有d 函数的奇异性,格林公式不能用。解决的办法是先从区域T中挖去包含r0的小体积,例如半径为 e 的小球Ke(图12-1),Se 的边界面为Se。对于剩下的体积,格林公式成立,
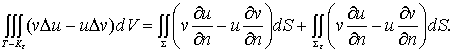 (12-1-8)
(12-1-8)
把(12-1-8)代入挖去Ke 的(12-1-7),并注意r≠r0,故 d(r-r0)=0,于是
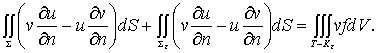 (12-1-9)
(12-1-9)
当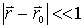 ,方程(12-1-6)的解 v(r,r0)—→ 位于点r0而电量为 -e 0 的点电荷的静电场中的电势,即-1/4p
,方程(12-1-6)的解 v(r,r0)—→ 位于点r0而电量为 -e 0 的点电荷的静电场中的电势,即-1/4p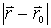 。令 e→0,得
。令 e→0,得
(12-1-9)右边—→ 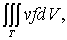
左边的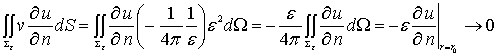
左边的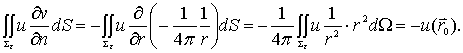
(12-1-10)
这样,(12-1-7)成为
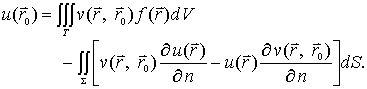 (12-1-11)
(12-1-11)
(12-1-11)称为泊松方程的基本积分公式。
(12-1-11)将(12-1-4)的解u用区域 T 上的体积分及其边界上的面积分表示了出来。那么,能否用(12-1-11)来解决边值问题呢?我们看到,(12-1-11)中需要同时知道u及  在边界 S上的值,但是,在第一边值问题中,已知的只是 u 在边界 S上的值;在第二边值问题中,已知的只是
在边界 S上的值,但是,在第一边值问题中,已知的只是 u 在边界 S上的值;在第二边值问题中,已知的只是  在边界S上的值。在第三边值问题中,已知的是u和
在边界S上的值。在第三边值问题中,已知的是u和  的一个线性关系在边界 S上的值,三类边界条件均未同时分别给出u和
的一个线性关系在边界 S上的值,三类边界条件均未同时分别给出u和  的边界 S上的值。因此,我们还不能直接利用(12-1-11)解决三类边值问题。
的边界 S上的值。因此,我们还不能直接利用(12-1-11)解决三类边值问题。
其实,这里距离问题的解决已经很近了。原来,对于函数v(r,r0),我们还只考虑其满足方程(12-1-6)。如果我们对v(r,r0)提出适当的边界条件,则上述困难就得以解决。
对于第一边值问题,u在边界 S上的值是已知的函数 j(M)。如果要求v满足齐次的第一类边界条件
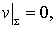 (12-1-12)
(12-1-12)
则(12-1-11)中含  的一项等于零。从而不需要知道
的一项等于零。从而不需要知道  在边界 S上的值。满足方程(12-1-6)及边界条件(12-1-12)的解称为泊松方程第一边值问题的格林函数,用G(r,r0)表示。这样,(12-1-11)式成为
在边界 S上的值。满足方程(12-1-6)及边界条件(12-1-12)的解称为泊松方程第一边值问题的格林函数,用G(r,r0)表示。这样,(12-1-11)式成为
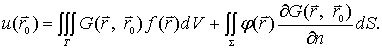 (12-1-13)
(12-1-13)
对于第三边值问题,令v满足齐次的第三类边界条件,
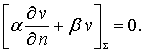 (12-1-14)
(12-1-14)
满足方程(12-1-6)及边界条件(12-1-14)的解称为泊松方程第三类边值问题的格林函数,也用G(r,r0)表示。以G(r,r0)乘(12-1-5)式两边,得
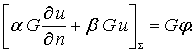
又以 u 乘(12-1-14),并以 G 代替其中的 v,得
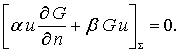
将这两式相减,得
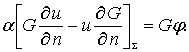
将此式代入(12-1-11),得
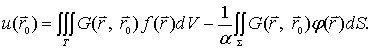 (12-1-15)
(12-1-15)
至于第二边值问题,表面看来,似乎可以按上述同样的办法来解决,即令G为定解问题
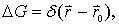 (12-1-16)
(12-1-16)
 (12-1-17)
(12-1-17)
的解,而由(12-1-11)得到
 (12-1-18)
(12-1-18)
可是,定解问题(12-1-16)~(12-1-17)的解不存在。这在物理上是容易理解的:不妨把这个格林函数看作温度分布。泛定方程(12-1-16)右边的 d 函数表明在 S 所围区域 T 中有一个点热源。边界条件(12-1-17)表明边界是绝热的。点热源不停地放也热量。而热量又不能经由边界散发出去,T 里的温度必然要不停地升高,其分布不可能是稳定的。这就需要引入推广的格林函数。对于三维空间,
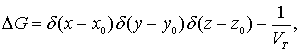
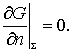
式中VT 是T 的体积。对于二维空间,
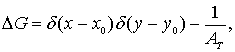
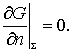
式中 AT 是 T 的面积,方程右边添加的项是均匀分布的热汇密度,这些热汇的总体恰好吸收了点热源所放出的热量,不多也不少。
(12-1-13)和(12-1-15)的物理解释有一个困难。公式左边u的宗量r0 表明观测点在r0,而右边积分中的f(r)表示源在r,可是,格林函数G(r,r0)所代表的是r0的点源在r点产生的场。这个困难如何解决呢?原来,这个问题里的格林函数具有对称性G(r,r0)=G(r0,r),将(12-1-13)和(12-1-15)中的r和r0对调,并利用格林函数的对称性,(12-1-13)成为
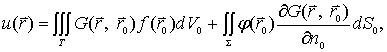 (12-1-19)
(12-1-19)
这就是第一边值问题解的积分表示式。(12-1-15)成为
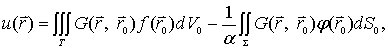 (12-1-20)
(12-1-20)
这就是第三边值问题解的积分表示式。
(12-1-19)和(12-1-20)的物理意义就很清楚了,右边第一个积分表示区域T中分布的源f(r0)在r点产生的场的总和。第二个积分则代表边界上的状况对r点场的影响的总和。两项积分中的格林函数相同。这正说明泊松方程的格林函数是点源在一定的边界条件下所产生的场。
现在来证明格林函数的对称性。在 T 中任取两个定点r1和r2。以这两点为中心,各作半径为 e 的球面 S1和 S 2。从 T 挖去 S 1和 S 2 所围的球K1和K2。在剩下的区域T-K1-K2上,G(r,r1)和G(r,r2)并无奇点。以u=G(r,r1),v=G(r,r2)代入格林公式(12-1-3)
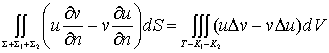
由于G(r,r1)和G(r,r2)是调和函数,上式右边为零。又由于格林函数的边界条件,上式左边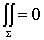 。这样
。这样
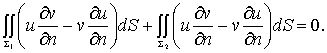
令e →0,上式成为0-v(r1)+u(r2)-0=0,即G(r1,r2)=G(r2,r1)。
对于拉普拉斯方程,即(12-1-4)式右边的 f(r)≡0,这时,我们只要令(12-1-19)和(12-1-20)两式右边的体积分值等于零,便可得到拉普拉斯方程第一边值问题的解
 (12-1-21)
(12-1-21)
以及第三边值问题的解
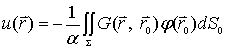 (12-1-22)
(12-1-22)
我们看到,借助格林公式,也可利用格林函数方法得到齐次方程定解问题的解。
第五章 变分法 泛函求导;泛函的极值问题;Euler-Lagrange 方程;Lagrange 乘子理论。变分法(calculus of variations),是处理函数的变量的数学领域,和处理数的函数的普通微积分相对。譬如,这样的泛函可以通过未知函数的积分和它的导数来构造。变分法最终寻求的是极值函数:它们使得泛函取得极大或极小值。有些曲线上的经典问题采用这种形式表达:一个例子是最速降线,在重力作用下一个粒子沿着该路径可以在最短时间从点A到达不直接在它底下的一点B。在所有从A到B的曲线中必须极小化代表下降时间的表达式。
第二篇:数学物理方程报告
平流方程.这个方程是:
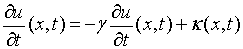 (1)
(1)
其中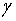 是一个正常数,
是一个正常数,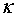 是
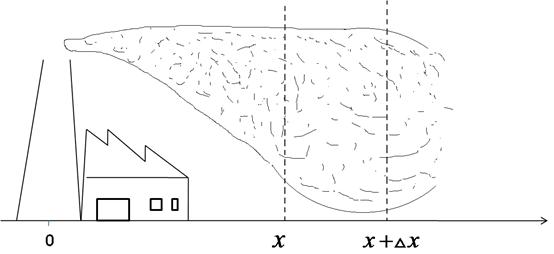
是 的函数.这个方程可以用来模拟艾滋病的传播、流体动力学,以及其他有关空气或水中的物质流动问题.作为具体的应用,考察风的运动,假设风沿着某个方向运动,比如
的函数.这个方程可以用来模拟艾滋病的传播、流体动力学,以及其他有关空气或水中的物质流动问题.作为具体的应用,考察风的运动,假设风沿着某个方向运动,比如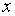 轴的正方向,其速度为每秒
轴的正方向,其速度为每秒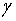 米.设在原点处有一工厂,风从工厂处携带一些污染物.令
米.设在原点处有一工厂,风从工厂处携带一些污染物.令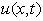 表示
表示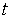 时刻
时刻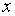 处的污染物的(线)密度(每米的颗粒个数).再设污染颗粒以正比于
处的污染物的(线)密度(每米的颗粒个数).再设污染颗粒以正比于 的速度掉下来,比例常数是
的速度掉下来,比例常数是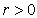 ,则
,则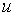 满足方程(1),
满足方程(1), .
.
(a)试证方程
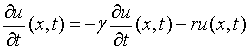
的所有解都具有形式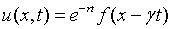 .
.
(b)令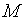 是初始时刻空气中的总颗粒数.试证:在时刻
是初始时刻空气中的总颗粒数.试证:在时刻 空气中的总颗粒数是
空气中的总颗粒数是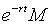 .
.
--------------------------------------------------------------------------
对于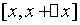 段
段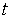 到
到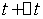 时间段内的颗粒物数有以下关系
时间段内的颗粒物数有以下关系
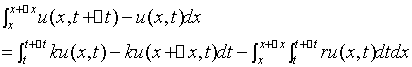
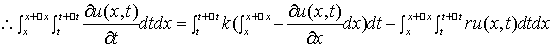
由于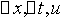 任意性知
任意性知
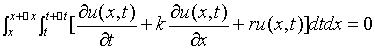
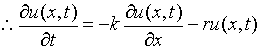
----------------------------------------------------------------------------
推导过程
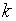 为风速
为风速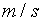 ,
,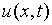 为
为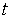 时刻
时刻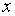 处的污染的(线)物密度(每米的颗粒个数),则
处的污染的(线)物密度(每米的颗粒个数),则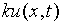 为单位时间内
为单位时间内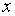 处的颗粒数
处的颗粒数
----------------------------------------------------------------------------------------------
研究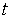 到
到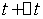 段通过
段通过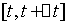 短的颗粒物。
短的颗粒物。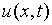 为
为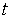 时刻
时刻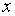 处的颗粒物(线)密度
处的颗粒物(线)密度
 为
为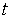 时刻
时刻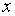 到
到 段内的颗粒物
段内的颗粒物
----------------------------------------------------------------------------------------
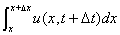 为
为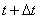 的间段
的间段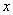 到
到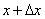 段内的颗粒物
段内的颗粒物
从而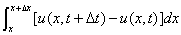 表示
表示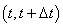 时间段内
时间段内
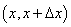 段颗粒物的变化量
段颗粒物的变化量
则 为
为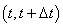 时间段内吹过
时间段内吹过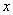 处的颗粒物
处的颗粒物
则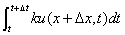 为
为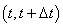 时间段内吹过
时间段内吹过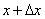 处的颗粒物
处的颗粒物
污染颗粒以正比于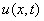 的速度下落比例常数为
的速度下落比例常数为
则下落速度为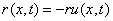
从而在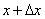 段内
段内 到
到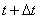 的间段下落的颗粒物总数
的间段下落的颗粒物总数
为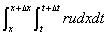
由于总颗粒物的变化量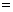 吹入
吹入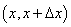 的颗粒物
的颗粒物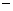 吹出
吹出
的颗粒物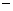 下落的颗粒物
下落的颗粒物
 可得
可得
-
数学读书报告
数学建模读书报告读数学中的美吴振奎吴旻著五月中旬我阅读了吴振奎吴旻两位先生所著的数学中的美一书书中从简洁和谐奇异三个方面记述了数学…
-
数学读书报告
数学读书报告中国数学简史姓名刘晓玥班级人管1031班学号1021053126数学我以前并不怎么喜欢它直到数学老师让我们看关于数学的…
-
数学读书报告
数学读书报告看完了一本书,名叫《数学与艺术——无穷的碎片》.这本书包含了十个章节,参考文献以及索引三大部分,是我从未见过的创新.这…
-
数学思维教育读书报告
摘要数学与思维读书报告摘要众所周知数学是人类文明的一个重要组成部分也是几千年来人类智慧的结晶数学思维除了具有概括性和间接性等特点外…
-
《数学与文化》读书报告
数学与文化读书报告通信工程学院专业一作者简介齐民友安徽芜湖人中国数学家19xx年加入中国共 产 党19xx年毕业于武汉大学数学系历…
-
数学物理方法总结(改)
数学物理方法总结第一章复变函数复数的代数式zxiy复数的三角式和指数式zcossin和zei1izeeiz2i欧拉公式1izcos…
-
数学物理方法大总结
数学物理方法一填空题1函数为0ettx1dtx0又称为第二类欧拉积分的为zettz1dtRez002B函10数又称为第一类欧拉积分…
-
数学物理方程小结
数学物理方程小结第七章数学物理定解问题数学物理定解问题包含两个部分数学物理方程即泛定方程和定解条件71数学物理方程的导出一般方法第…
-
0 数学物理方程概述
数学物理方程概述什么是数学物理方程或数学物理方程是研究什么的关于方程含有未知数的等式叫做方程方程有多种多样例如函数方程含有未知函数…
-
数学物理方程期末考试试题及答案
一求解方程15分数学物理方程期末考试试题及答案utta2uxx0uxat0xuxat0x其中00解设xat则方程变为xatu0uF…
-
数学分析读书报告
数学读书报告对数学分析六个基本定理的感想课程名称数学文化学生姓名代广武学生学号20xx303630____专业应用物理学所在院系理…