弹簧振子
教案示例
——简谐运动
一、教学目标
1.在物理知识方面要求:
(1)了解什么是机械振动;
(2)掌握简谐运动回复力的特征;
(3)掌握在一次全振动过程中回复力、加速度、速度随偏离平衡位置的位移变化的规律(定性).
2.通过观察演示实验,概括出机械振动的特征,培养学生的观察、概括能力;通过相关物理量变化规律的学习,培养分析、推理能力.
3.渗透物理学方法的教育,运用理想化方法,突出主要因素,忽略次要因素,抽象出物理模型——弹簧振子,研究弹簧振子在理想条件下的振动.
二、重点、难点分析
1.重点是使学生掌握简谐运动的回复力特征及相关物理量的变化规律.回复力的特征是形成加速度、速度、位移等物理量周期性变化的原因.
2.偏离平衡位置的位移与运动学中的位移概念容易混淆,这是难点.在一次全振动中速度的变化(大小、方向)较复杂,比较困难.
三、教具
1.演示机械振动
钢板尺、铁架台、单摆、竖直弹簧振子、皮筋球.
气垫弹簧振子、微型气源.
2.分析相关物理量的变化
计算机、软盘、彩电(29吋,代彩显),投影幻灯、投影片、彩笔.
四、主要教学过程
(一)引入新课
我们学习机械运动的规律是从简单到复杂:匀速运动、匀变速直线运动、平抛运动、匀速圆周运动,今天学习一种更复杂的运动——简谐运动.
(二)教学过程设计
1.机械振动
振动是自然界中普遍存在的一种运动形式,请同学举例说明什么样的运动是振动?
说明微风中树枝的颤动、心脏的跳动、钟摆的摆动、声带的振动??这些物体的运动都是振动.
演示几个振动的实验,要求同学边看边想:物体振动时有什么特征?
(1)一端固定的钢板尺
(2)单摆

(3)弹簧振子
(4)穿在橡皮绳上的塑料球
提出问题:这些物体的运动各不相同:运动轨迹是直线的、曲线的;运动方向水平的、竖直的;物体各部分运动情况相同的、不同的??它们的运动有什么共同特征?

在同学回答的基础上归纳出:物体振动时有一中心位置,物体(或物体的一部分)在中心位置两侧做往复运动,振动是机械振动的简称.
明确:物体(或物体的一部分)在某一中心位置两侧所做的往复运动,叫做机械振动
2.简谐运动
指出简谐运动是一种最简单、最基本的振动,我们以弹簧振子为例学习简谐运动.
(1)弹簧振子
演示气垫弹簧振子的振动.
通过同学的观察、分析、讨论得到:
①滑块的运动是平动,可以看作质点.
②弹簧的质量远远小于滑块的质量,可以忽略不计.
明确:一个轻质弹簧联接一个质点,弹簧的另一端固定,就构成了一个弹簧振子.
③没有气垫时,阻力太大,振子不振动;有了气垫时,阻力很小,振子振动. 说明我们研究在没有阻力的理想条件下弹簧振子的运动.
(2)弹簧振子为什么会振动?
提出问题:当把振子从它静止的位置O拉开一小段距离到B再放开后,它为什么会在B—O—C之间振动呢?
要求同学运用学过的力学知识认真分析、思考.
引导同学分析振子受力及从B→O→C→O→B的运动情况,突出弹力的方向及在O点振子由于惯性继续运动.
归纳得到:物体做机械振动时,一定受到指向中心位置的力,这个力的作用总能使物体回到中心位置,这个力叫回复力.回复力是根据力的效果命名的,对于弹簧振子,它是弹力.
说明回复力可以是弹力,或其它的力,或几个力的合力,或某个力的分力.
在O点,回复力是零,叫振动的平衡位置.
(3)简谐运动的特征
说明弹簧振子在振动过程中,回复力的大小和方向与振子偏离平衡位置的位移有直接关系.在研究机械振动时,我们把偏离平衡位置的位移简称为位移. 演示:计算机模拟弹簧振子的振动

引导同学分析、讨论:
振子从B运动到E时,位移大小为|OE|,方向向右;
振子从C运动到D时,位移大小为|OD|,方向向左;
振子运动到O时,位移为零;
位移可以用振子坐标x来表示.
提出问题:弹簧振子振动时,回复力与位移是什么关系?
归纳同学的回答得到:根据胡克定律,弹簧振子的回复力与位移成正比,与位移方向相反.
明确:物体在跟位移大小成正比,并且总指向平衡位置的力作用下的振动,叫做简谐运动.
写出F=-kx
说明式中F为回复力;x为偏离平衡位置的位移;k是常数,对于弹簧振子,k是劲度系数,对于其他物体的简谐运动,k是别的常数;负号表示回复力与位移的方向总相反.
弹簧振子的振动只是简谐运动的一种.
3.在一次全振动中,相关物理量的变化规律
演示:计算机模拟弹簧振子的振动.(与前面相似,加x、v、a、F的显示) 让同学观察当振子从B→O→C→O→B时,就完成了一次全振动,以后振子会重复上述过程.
(1)位移的变化 演示:x的变化. (2)回复力的变化
提出问题:当位移x变化时,回复力F如何变化?
在同学回答的基础上明确:根据简谐运动的特征,F与x成正比变化,且方向相反演示:F的变化. (3)加速度的变化
提出问题:当回复力F变化时,加速度α如何变化?
在同学回答的基础上明确:根据牛顿第二定律,a与F成正比,且方向相同. 演示:a的变化. (4)速度的变化
引导同学分析讨论:B→O振子怎样运动?
明确:是加速度变小的加速运动,速度v变大,O速度最大. 再分析讨论:O→C振子做什么运动?
明确:是加速度变大的减速运动,速度v变小,C速度为零. 演示:v的变化.
发给同学表格,并将表格用投影幻灯投影在幕上.
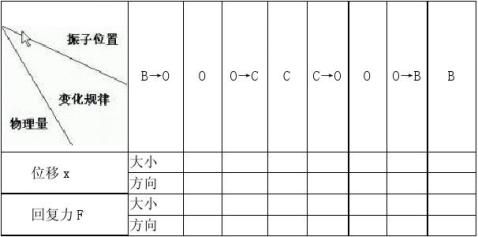

符号约定:增大↑ 减小↓ 最大M 零0 向左← 向右→ 要求同学填写指定表格,讨论1~2名同学的所填内容是否正确. (三)课堂小结
1.机械振动是一种很普遍的运动形式,大至地壳的振动,小至分子、原子的振动.振动的特征是在中心位置两侧往复运动.
2.为了研究简谐运动,我们运用了物理学中的理想化方法:从最简单、最基本的情况入手,抓住影响运动的主要因素,去掉次要的、非本质因素的干扰,建立了理想化的物理模型——弹簧振子,并且研究了弹簧振子在无阻力的理想条件下的运动问题,理想化是研究物理问题常用的方法之一.
3.简谐运动是一种简单的、基本的振动,许多物体的微小振动都可以看作是简谐运动,复杂的振动可以看作简谐运动的叠加,它的特征是:回复力与偏离平衡位置的位移成正比.
4.简谐运动是一种变加速运动. 五、说明
1.简谐运动中振子的“位移”x实质是位置矢量,与运动学中讲的位移矢量不同,中学没有严格区分这两个矢量,我们通俗地把x说成是相对于平衡位置的位移.
2.弹簧振子振动形成的原因,一是回复力的特点(总指向平衡位置),二是振子的惯性,这是分析问题的关键.
3.振动物体过平衡位置对回复力是零,合力不一定是零,所以,我们给机械振动下定义时用的是中心位置,较为准确.教材用平衡位置
第二篇:弹簧振子振动周期的讨论
弹簧振子周期公式的探究
梅丹兵(21610115)
(东南大学交通学院,南京市,210000)
摘 要: 基于本学期在“弹簧振子周期”实验中出现的实验数据和理论数据相差较大的缘故,本文探究了在“弹簧振子周期”实验中弹簧质量对系统周期的影响,并利用数学知识推导出了一个符合实验数据的合理公式。
关键词: 振动周期;弹簧振子;有效质量;非线性改变
A discussion on the cycle of vibration of springs
Mei Danbing
(Transportation Institute of SEU , Nanjing 210000)
Abstract: Based on the reason that the big difference between the experimental data and the theoretical data in the experiment about “the cycle of vibration of springs “,the article explored the influence of the quality of springs on the vibration cycle ,and made full use of the mathematical knowledge to derive a rational formula in line with experimental data.
key words: Vibration cycle ; springs ;effective quality ; Non-linear change
引言
在本学期的“简谐振动”一章中我们学习了弹簧振子周期公式,并做了相关的物理实验。根据课本上简谐运动的周期公式可推导出弹簧振子的振动周期公式为
 (1)
(1)
其中M为振子质量,K为弹簧劲度系数。
而我们发现由(1)式计算出得的理论值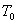 与实验测得的测量值
与实验测得的测量值
 之间的偏差达到了2.58%,其中固然有测量误差和阻力误差,但不可排除的是(1)式中的M仅指振子的质量,而没有考虑弹簧的质量。由于本实验中弹簧劲度系数K与振子质量M都很小,这时弹簧自身的质量已不能忽略。那么如何考虑弹簧质量对系统周期的影响呢?假如弹簧的质量为m,可以肯定
之间的偏差达到了2.58%,其中固然有测量误差和阻力误差,但不可排除的是(1)式中的M仅指振子的质量,而没有考虑弹簧的质量。由于本实验中弹簧劲度系数K与振子质量M都很小,这时弹簧自身的质量已不能忽略。那么如何考虑弹簧质量对系统周期的影响呢?假如弹簧的质量为m,可以肯定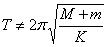 ,因为弹簧虽参与振动,但其上各点的振动情况是不一样的。通过查阅相关文献我们得知此时系统的振动周期为
,因为弹簧虽参与振动,但其上各点的振动情况是不一样的。通过查阅相关文献我们得知此时系统的振动周期为
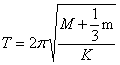 (2)
(2)
于是在原实验基础上,我们测量了弹簧的质量m,并再次将相关数据代入(2)式,计算得出的理论值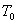 与实际测量值
与实际测量值 之间还是有近1.93%的偏差,这一结果的得出不得不引起我对(2)式的质疑。带着疑惑我再次详细的查看了相关文献中(2)式的推导过程,发现了可能造成偏差的主要原因——线弹性变化。通过咨询老师和查阅相关资料,发现弹簧的变化严格意义上不是均匀的,所以(2)式的推导过程严格意义上是不精确的。但我们有理由相信,通过物理模型和相关数学知识,会得到比(2)式更为精确的公式。
之间还是有近1.93%的偏差,这一结果的得出不得不引起我对(2)式的质疑。带着疑惑我再次详细的查看了相关文献中(2)式的推导过程,发现了可能造成偏差的主要原因——线弹性变化。通过咨询老师和查阅相关资料,发现弹簧的变化严格意义上不是均匀的,所以(2)式的推导过程严格意义上是不精确的。但我们有理由相信,通过物理模型和相关数学知识,会得到比(2)式更为精确的公式。
 梅丹兵,男,1991年11月2日生于湖北黄冈,现就读于东南大学交通学院,主修岩土工程。 E-amil :meidanbing@yahoo.com.cn
梅丹兵,男,1991年11月2日生于湖北黄冈,现就读于东南大学交通学院,主修岩土工程。 E-amil :meidanbing@yahoo.com.cn
弹簧振子系统周期公式的理论推导
首先来探讨当弹簧末端不加任何物体时其振动周期的表达式。
 设有一总长度为L,质量为m,劲度系数为k的弹簧一端固定,另一端自由(如图1所示),其振动的固有周期到底为多少呢?
设有一总长度为L,质量为m,劲度系数为k的弹簧一端固定,另一端自由(如图1所示),其振动的固有周期到底为多少呢?
此处我们通过物理学驻波模型来解决此问题。
设另有一根总长度很长的弹簧,其质量均匀分布,且弹簧单位长度的质量为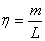 ,劲度系数为
,劲度系数为 (查阅相关文献知影响弹簧劲度系数K的因素很多,此处可以通过改变不同的因素来达到目的)。让这根弹簧两端以相同的振幅和频率沿弹簧方向振动起来,稳定后必然在弹簧上形成驻波。调节波源频率,使长弹簧的波长恰好为4L,则相邻波腹与波节的距离恰好为L。由于驻波的波节振幅为零,与图1弹簧的固定点O一样;驻波的波腹振幅最大,与自由点P一样,可得图1弹簧的振动与长弹簧波节到相邻波腹振动情况完全一样(因周期只与M和K有关,弹簧长度的不同不影响结果)。
(查阅相关文献知影响弹簧劲度系数K的因素很多,此处可以通过改变不同的因素来达到目的)。让这根弹簧两端以相同的振幅和频率沿弹簧方向振动起来,稳定后必然在弹簧上形成驻波。调节波源频率,使长弹簧的波长恰好为4L,则相邻波腹与波节的距离恰好为L。由于驻波的波节振幅为零,与图1弹簧的固定点O一样;驻波的波腹振幅最大,与自由点P一样,可得图1弹簧的振动与长弹簧波节到相邻波腹振动情况完全一样(因周期只与M和K有关,弹簧长度的不同不影响结果)。
下面从驻波行程条件来求解周期T
由于固体中纵波的波速为
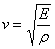 (3)
(3)
其中E为弹簧弹性模量,ρ为密度,对于长度为L的上述弹簧,通过查阅资料得其等效密度和弹性模量分别为:
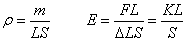
其中S为弹簧横截面积。
将其代入(3)式得:
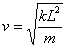 (4)
(4)
欲使弹簧波波长为4L,则图1弹簧的固有周期为:
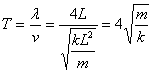 (5)
(5)
由此可知 的结论是错误的。(2)式之所以会出错,是因为其在考虑振动速度时,直接认为速度是线性变化的。但事实上当弹簧的质量不能忽略时,其形变量是不均匀的,离固定点O越近的地方由于受到的弹力越大,形变量也就越大(示意图如图2所示)。那么“一质量为
的结论是错误的。(2)式之所以会出错,是因为其在考虑振动速度时,直接认为速度是线性变化的。但事实上当弹簧的质量不能忽略时,其形变量是不均匀的,离固定点O越近的地方由于受到的弹力越大,形变量也就越大(示意图如图2所示)。那么“一质量为 的弹簧与一质量为
的弹簧与一质量为 的振子组成的‘弹簧振子’振动周期”为多少呢?
的振子组成的‘弹簧振子’振动周期”为多少呢?
 设某时刻物体M离开其平衡位置的位移为
设某时刻物体M离开其平衡位置的位移为 ,速度为
,速度为 ,加速度为
,加速度为 ;而距O点为l的一小段弹簧
;而距O点为l的一小段弹簧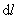 离开其平衡位置的位移为
离开其平衡位置的位移为 ,速度为
,速度为 ,加速度为
,加速度为 。由于所有质点的振动情况都同相,则可以得出:
。由于所有质点的振动情况都同相,则可以得出: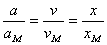 。又由于每一段弹簧离开平衡位置的位移都等于它左侧所有小段的伸长量之和,则距O点为l的一小段弹簧
。又由于每一段弹簧离开平衡位置的位移都等于它左侧所有小段的伸长量之和,则距O点为l的一小段弹簧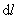 的伸长量为
的伸长量为 ,劲度系数为
,劲度系数为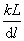 ,则其弹力为
,则其弹力为 ,质量为
,质量为 。其与相邻小段弹簧的弹力差,即其所受合力
。其与相邻小段弹簧的弹力差,即其所受合力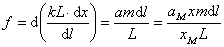
化简可得:
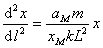
由于M物体振动时的 与
与 反向,即
反向,即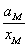 为负值,则根据常微分方程的理论,上面微分方程的解可写作
为负值,则根据常微分方程的理论,上面微分方程的解可写作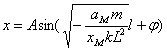 。其中A为与M离开平衡位置的位移有关的变量,由于O点附近的质元离其平衡位置的位移趋向于零,可得
。其中A为与M离开平衡位置的位移有关的变量,由于O点附近的质元离其平衡位置的位移趋向于零,可得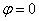 。
。
即: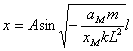 (6)
(6)
则每一小段弹簧的形变量为
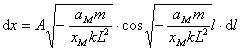
相应的小段弹簧弹力为
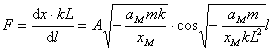
(7)
对于连接M物体的那小段弹簧,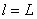 ,代入(7)式得
,代入(7)式得
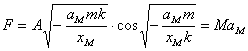 (8)
(8)
下面分三种情况对(8)式进行导论
Ⅰ. 当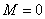 时,即没有物体M时:
时,即没有物体M时:
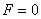
由(8)式得:
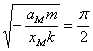
解得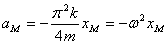 (9)
(9)
于是: (10)
(10)
得到与(5)式相同的结论。
Ⅱ. 当 时,即弹簧质量忽略时,
时,即弹簧质量忽略时,

则每一小段弹簧的形变量 都相等,即弹簧的形变是均匀的,此时的弹簧振子即我们平时看到的弹簧质量可忽略的理想弹簧振子,其振动周期为
都相等,即弹簧的形变是均匀的,此时的弹簧振子即我们平时看到的弹簧质量可忽略的理想弹簧振子,其振动周期为
得到与(1)式相同的结论。
Ⅲ. 当 时,由(8)式得:
时,由(8)式得: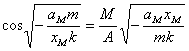 (11)
(11)
由(6)式得: (12)
(12)
设 ,将之与(12)式一起代入(11)式得:
,将之与(12)式一起代入(11)式得:
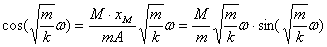 从而得到:
从而得到:
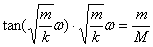 (13)
(13)
上式中M、m、k为定值, 为我们所求弹簧振子的圆频率。显然只有当
为我们所求弹簧振子的圆频率。显然只有当 为特殊值时,该超越方程才有精确解,否则只能是近似解。
为特殊值时,该超越方程才有精确解,否则只能是近似解。
例如:
当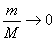 ,即
,即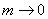 时,
时,
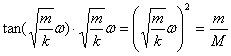 (14)
(14)
化简得: 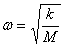
从而得到 
此即理想弹簧振子的圆频率。
当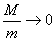 ,即
,即 时,
时,


即可得与(10)式一样的结论。
当 ,
,
还有等等…
结果分析
在推导出(13)式之后,我重新将各数据代入到公式中,计算得出的近似理论值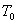 与测量值
与测量值 的偏差缩小到了1.52%.虽然较之前只减小了不到0.4%,但这样的数据还是更为合理。
的偏差缩小到了1.52%.虽然较之前只减小了不到0.4%,但这样的数据还是更为合理。
结论
本文的论述过程是建立在弹簧的非线性形变基础和微积分公式之上,因此推理过程有些复杂,但,思路较为清晰、缜密,不失为一种好的论证过程。同时由推导过程知,在振子质量M和劲度系数K不变的前提下,弹簧质量m越大,采用(13)式与采用(2)式计算得出的理论值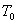 之间的偏差越大。因此,我们在处理弹簧振子周期问题时,当弹簧的质量与振子的质量相比基本可以忽略时,计算系统振动周期,可以近似的采用公式
之间的偏差越大。因此,我们在处理弹簧振子周期问题时,当弹簧的质量与振子的质量相比基本可以忽略时,计算系统振动周期,可以近似的采用公式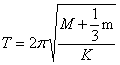 ;但当弹簧的质量不可忽略且对实验的要求较高时,采用公式
;但当弹簧的质量不可忽略且对实验的要求较高时,采用公式  所求出的结果更为精确。
所求出的结果更为精确。
参考文献:
[1] 马文蔚等,物理学.第五版,高等教育出版社,2006,3(5):1-6,64-69
[2] 钱锋,潘人培. 大学物理实验.修订版 ,高等教育出版,2005,11. 73-76
[3] 徐滔滔,《大学物理实验》期刊,1998年6月,第11卷,第2期:《关于弹簧振子振动周期的讨论》
[4] 杨桂通,弹性力学简明教程,清华大学出版社,2006,9:48-51
[5] 陈学志,罗莹,《中国现代教育装备》,20##年08期:《探究弹簧劲度系数的影响因素》
-
弹簧振子实验报告
弹簧振子实验报告一引言实验目的1测定弹簧的刚度系数stiffnesscoefficient2研究弹簧振子的振动特性验证周期公式3学…
-
实验报告模板--弹簧振子(完成版)
北京师范大学物理实验教学中心基础物理实验实验题目实验记录1仪器与用具弹簧振子周期经验公式的总结2实验内容和数据记录a测量弹簧振子的…
-
弹簧振子实验报告
浙江师范大学实验报告实验名称弹簧振子的研究班级综合理科121班姓名周琚学号12990141同组人实验日期20xx年10月10日室温…
-
实验报告-弹簧振子
北京师范大学物理实验教学中心基础物理实验实验题目弹簧振子周期经验公式的总结实验记录1仪器与用具2实验内容和数据记录a测量弹簧振子的…
-
气垫弹簧振子的简谐振动实验报告
大学实验报告学院系物理系专业年级级姓名学号实验时间指导教师签名实验四气垫弹簧振子的简谐振动一实验目的与要求1考察弹簧振子的振动周期…
-
怎样才能做好高中数学总结
怎样才能做好高中数学的总结摘要:学生的学习,其特点是在教师的指导下,在学习知识的基础上发展自己的认识知识、创新知识的能力。在教学过…
-
大三个人总结
0894042228余晴大三学年个人总结转眼三年的大学生活已经结束了,几年的财会专业知识学习和丰富的课余社会实践经历,培养了我对财…
-
企业培训师知识点总结
1、信息搜集要尽量全面;2、信息搜集要准确;3、信息的整理要清楚。2、岗位信息搜集工作的方法:1、观察法(主要用于观察、记录、核实…
-
读书活动总结
五大连池市四平学校“最是书香能致远,读书之乐乐无穷。”为进一步激发学生读书热情,活跃校园文化,树立正气,营造良好的读书氛围。我们精…
-
体育教学个人实习总结
两个月的实习时间已经结束,在这两个月的时间里,我付出了很多,同时也得到了很大的收获,我在实习的这段时间里,我担任的是刘老师指导小组…