高中数学选修2-1、2-2知识点小结
选修2-1、2-2知识点
选修2-1
第一章 常用逻辑用语
1. 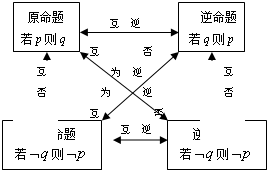 命题及其关系
命题及其关系
① 四种命题相互间关系:
② 逆否命题同真同假
2. 充分条件与必要条件
 是
是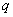 的充要条件:
的充要条件: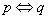
 是
是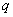 的充分不必要条件:
的充分不必要条件:
 是
是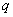 的必要不充分条件:
的必要不充分条件:
 是
是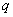 的既充分不必要条件:
的既充分不必要条件:
3. 逻辑联结词 “或”“且”“非”
4. 全称量词与存在量词 注意命题的否定形式(联系反证法的反设),主要是量词的变化.
第二章 圆锥曲线与方程
1. 三种圆锥曲线的性质(以焦点在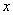 轴为例)
轴为例)

2. “回归定义” 是一种重要的解题策略。如:(1)在求轨迹时,若所求的轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的方程,写出所求的轨迹方程;(2)涉及椭圆、双曲线上的点与两个焦点构成的焦点三角形问题时,常用定义结合解三角形(一般是余弦定理)的知识来解决;(3)在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形利用几何意义去解决。
3. 直线与圆锥曲线的位置关系
(1)有关直线与圆锥曲线的公共点的个数问题,直线与圆锥曲线的位置关系有三种情况:相交、相切、相离.联立直线与圆锥曲线方程,经过消元得到一个一元二次方程(注意在和双曲线和抛物线方程联立时二次项系数是否为0),直线和圆锥曲线相交、相切、相离的充分必要条件分别是 、
、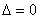 、
、 .
.
应注意数形结合(例如双曲线中,利用直线斜率与渐近线的斜率之间的关系考查直线与双曲线的位置关系)
常见方法:①联立直线与圆锥曲线方程,利用韦达定理等;
②点差法
(主要适用中点问题,设而不求,注意需检验,化简依据: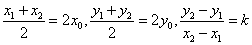 )
)
(2)有关弦长问题,应注意运用弦长公式及韦达定理来解决;(注意斜率是否存在)
① 直线具有斜率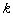 ,两个交点坐标分别为
,两个交点坐标分别为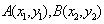
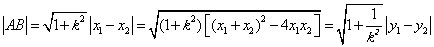
② 直线斜率不存在,则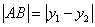 .
.
(3)有关对称垂直问题,要注意运用斜率关系及韦达定理,设而不求,简化运算。
考查三个方面:A 存在性(相交);B 中点;C 垂直(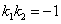 )
)
注: 1.圆锥曲线,一要重视定义,这是学好圆锥曲线最重要的思想方法,二要数形结合,既熟练掌握方程组理论,又关注图形的几何性质,以简化运算。
2.当涉及到弦的中点时,通常有两种处理方法:一是韦达定理;二是点差法.
3.圆锥曲线中参数取值范围问题通常从两个途径思考:一是建立函数,用求值域的方法求范围;二是建立不等式,通过解不等式求范围。
4.注意向量在解析几何中的应用(数量积解决垂直、距离、夹角等)
(4)求曲线轨迹常见做法:定义法、直接法(步骤:建—设—现(限)—代—化)、代入法(利用动点与已知轨迹上动点之间的关系)、点差法(适用求弦中点轨迹)、参数法、交轨法等。
第三章 空间向量与立体几何
1. 空间向量及其运算
① 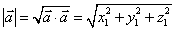 ,
,
② 共线向量定理: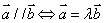
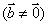
③ 共面向量定理: ;
;
四点共面
④ 空间向量基本定理 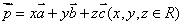 (不共面的三个向量
(不共面的三个向量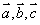 构成一组基
构成一组基
底,任意两个向量都共面)
2. 平行:(直线的方向向量,平面的法向量)( 是a,b的方向向量,
是a,b的方向向量, 是平面
是平面 的法向量)
的法向量)
线线平行: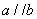

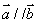
线面平行: 或
或 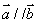 ,
,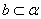 或
或 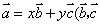 是
是 内不共线向量)
内不共线向量)
面面平行:
3. 垂直
线线垂直: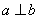

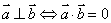
线面垂直: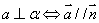 或
或  是
是 内不共线向量)
内不共线向量)
面面垂直:
4. 夹角问题
线线角 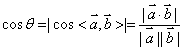 (注意异面直线夹角范围
(注意异面直线夹角范围 )
)
线面角 
二面角 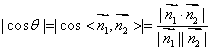 (一般步骤①求平面的法向量;②计算法向量夹角;③回答二面角(空间想象二面角为锐角还是钝角或借助于法向量的方向),只需说明二面角大小,无需说明理由))
(一般步骤①求平面的法向量;②计算法向量夹角;③回答二面角(空间想象二面角为锐角还是钝角或借助于法向量的方向),只需说明二面角大小,无需说明理由))
5. 距离问题(一般是求点面距离,线面距离,面面距离转化为点到面的距离)
P到平面 的距离
的距离 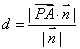 (其中
(其中 是平面
是平面 内任一点,
内任一点, 为平面
为平面 的法向量)
的法向量)
6. 立体几何解题一般步骤
坐标法:①建系(选择两两垂直的直线,借助于已有的垂直关系构造);②写点坐标;③写向量的坐标;④向量运算;⑤将向量形式的结果转化为最终结果。
基底法:①选择一组基底(一般是共起点的三个向量);②将向量用基底表示;③向量运算;④将向量形式的结果转化为最终结果。
几何法:作、证、求
异面直线夹角——平移直线(借助中位线平行四边形等平行线);
线面角——找准面的垂线,借助直角三角形的知识解决;
二面角——定义法作二面角,三垂线定理作二面角;作交线的垂面.
选修2-2
第一章 导数及其应用
1. 平均变化率 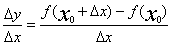
2. 导数(或瞬时变化率) 
导函数(导数): 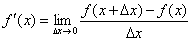
3. 导数的几何意义:函数y=f(x)在点x0处的导数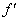 (x0)就是曲线y=f(x)在点(x0,f(x0))处的切线的斜率,即k=
(x0)就是曲线y=f(x)在点(x0,f(x0))处的切线的斜率,即k=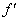 (x0).
(x0).
应用:求切线方程,分清所给点是否为切点
4. 导数的运算:
(1)几种常见函数的导数:
①(C)′=0(C为常数); ②( )′=
)′=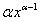 (x>0,
(x>0, ); ③(sinx)′=cosx;
); ③(sinx)′=cosx;
④(cosx)′=-sinx; ⑤(ex)′=ex; ⑥(ax)′=axlna(a>0,且a≠1);
⑦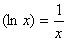 ; ⑧
; ⑧ (a>0,且a≠1).
(a>0,且a≠1).
(2)导数的运算法则:
①[u(x)±v(x)]′=u′(x)±v′(x); ②[u(x)v(x)]′=u′(x)v(x)+u(x)v′(x);
③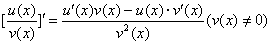 .
.
5. 设函数 在点
在点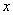 处有导数
处有导数 ,函数
,函数 在点
在点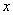 的对应点
的对应点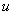 处有导数
处有导数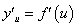 ,则复合函数
,则复合函数 在点
在点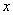 处也有导数,且
处也有导数,且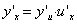 或
或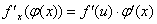 。复合函数对自变量的导数,等于已知函数对中间变量的导数,乘以中间变量对自变量的导数。
。复合函数对自变量的导数,等于已知函数对中间变量的导数,乘以中间变量对自变量的导数。
6. 定积分的概念,几何意义,区边图形的面积的积分形式表示,注意确定上方函数,下方函数的选取,以及区间的分割.微积分基本定理 .
.
物理上的应用:汽车行驶路程、位移;变力做功问题。
7. 函数的单调性
(1)设函数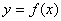 在某个区间(a,b)可导,如果
在某个区间(a,b)可导,如果
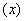
 ,则
,则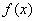 在此区间上为增函数;如果
在此区间上为增函数;如果
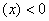 ,则
,则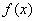 在此区间上为减函数;
在此区间上为减函数;
(2)如果在某区间内恒有
 ,则
,则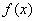 为常数。
为常数。
★★★反之,若已知可导函数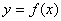 在某个区间上单调递增,则
在某个区间上单调递增,则 ,且不恒为零;可导函数
,且不恒为零;可导函数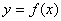 在某个区间上单调递减,则
在某个区间上单调递减,则 ,且不恒为零.
,且不恒为零.
求单调性的步骤:
① 确定函数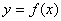 的定义域(不可或缺,否则易致错);
的定义域(不可或缺,否则易致错);
② 解不等式 ;
;
③ 确定并指出函数的单调区间(区间形式,不要写范围形式),区间之间用“,”★隔开,不能用“ ”连结。
”连结。
8. 极值与最值
对于可导函数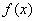 ,在
,在 处取得极值,则
处取得极值,则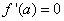 .
.
最值定理:连续函数在闭区间上一定有最大最小值.
若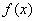 在开区间
在开区间 有唯一的极值点,则是最值点。
有唯一的极值点,则是最值点。
求极值步骤:
① 确定函数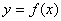 的定义域(不可或缺,否则易致错);
的定义域(不可或缺,否则易致错);
② 解不等式 ;
;
③ 检验 的根的两侧的
的根的两侧的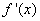 符号(一般通过列表),判断极大值,极小值,还是非极值点.
符号(一般通过列表),判断极大值,极小值,还是非极值点.
求最值时,步骤在求极值的基础上,将各极值与端点处的函数值进行比较大小,切忌直接说某某就是最大或者最小。
9. 恒成立问题 “ ”和“
”和“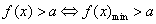 ”,注意参数的取值中“=”能否取到。
”,注意参数的取值中“=”能否取到。
第二章 推理与证明
1. 分清概念:合情推理与演绎推理
2. 综合法 分析法的步骤规范
3. 反证法 步骤:①提出反设;②推出矛盾 ;③肯定结论
4. 数学归纳法 步骤规范:(1)归纳奠基;(2)递推步骤
(最后一定说明当n=k+1时,结论成立,根据(1)(2),结论对于 (或者其他)成立,必不可少)
(或者其他)成立,必不可少)
第三章 数系的扩充与复数的引入
1. 复数的概念 三种表示形式:代数形式: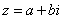 ,复平面内点Z(a,b),向量
,复平面内点Z(a,b),向量 .
.
2. 区分实数,虚数,纯虚数,复数
3. 复数的四则运算及其几何意义
4. 复数的模
第二篇:人教版高中数学选修2-1知识点小结
选修2-1知识点
选修2-1
第一章 常用逻辑用语
1、命题:用语言、符号或式子表达的,可以判断真假的陈述句.
真命题:判断为真的语句.
假命题:判断为假的语句.
2、“若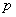 ,则
,则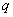 ”:
”: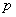 称为命题的条件,
称为命题的条件,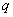 称为命题的结论.
称为命题的结论.
3、若原命题为“若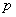 ,则
,则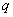 ”,则它的逆命题为“若
”,则它的逆命题为“若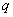 ,则
,则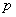 ”.
”.
4、若原命题为“若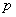 ,则
,则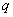 ”,则它的否命题为“若
”,则它的否命题为“若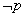 ,则
,则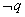 ”.
”.
5、若原命题为“若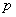 ,则
,则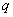 ”,则它的逆否命题为“若
”,则它的逆否命题为“若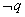 ,则
,则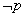 ”.
”.
6、四种命题的真假性:

四种命题的真假性之间的关系:
 两个命题互为逆否命题,它们有相同的真假性;
两个命题互为逆否命题,它们有相同的真假性;
 两个命题为互逆命题或互否命题,它们的真假性没有关系.
两个命题为互逆命题或互否命题,它们的真假性没有关系.
7、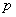 是
是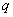 的充要条件:
的充要条件: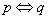
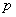 是
是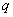 的充分不必要条件:
的充分不必要条件: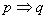 ,
,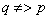
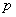 是
是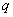 的必要不充分条件:
的必要不充分条件: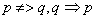
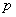 是
是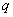 的既不充分不必要条件:
的既不充分不必要条件: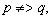
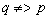
8、逻辑联结词:
(1)用联结词“且”把命题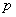 和命题
和命题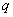 联结起来,得到一个新命题,记作
联结起来,得到一个新命题,记作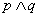 .全真则真,有假则假。
.全真则真,有假则假。
(2)用联结词“或”把命题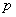 和命题
和命题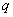 联结起来,得到一个新命题,记作
联结起来,得到一个新命题,记作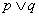 .全假则假,有真则真。
.全假则假,有真则真。
(2)对一个命题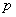 全盘否定,得到一个新命题,记作
全盘否定,得到一个新命题,记作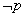 .真假性相反
.真假性相反
9、短语“对所有的”、“对任意一个”在逻辑中通常称为全称量词,用“ ”表示.
”表示.
含有全称量词的命题称为全称命题.
全称命题“对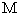 中任意一个
中任意一个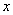 ,有
,有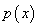 成立”,记作“
成立”,记作“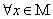 ,
,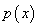 ”.
”.
短语“存在一个”、“至少有一个”在逻辑中通常称为存在量词,用“ ”表示.
”表示.
含有存在量词的命题称为特称命题.
特称命题“存在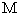 中的一个
中的一个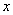 ,使
,使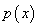 成立”,记作“
成立”,记作“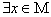 ,
,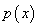 ”.
”.
10、全称命题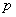 :
: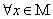 ,
,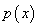 ,它的否定
,它的否定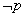 :
: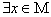 ,
,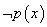 .全称命题的否定是特称命题.
.全称命题的否定是特称命题.
例:“a=1”是“ ”的( )
”的( )
A.充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
第二章圆锥曲线与方程
1、椭圆定义:平面内与两个定点 ,
,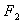 的距离之和等于常数(大于
的距离之和等于常数(大于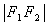 )的点的轨迹称为椭圆.这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.
)的点的轨迹称为椭圆.这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.
2、椭圆的几何性质:
3、平面内与两个定点 ,
, 的距离之差的绝对值等于常数(小于
的距离之差的绝对值等于常数(小于 )的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.
)的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.
4、双曲线的几何性质:
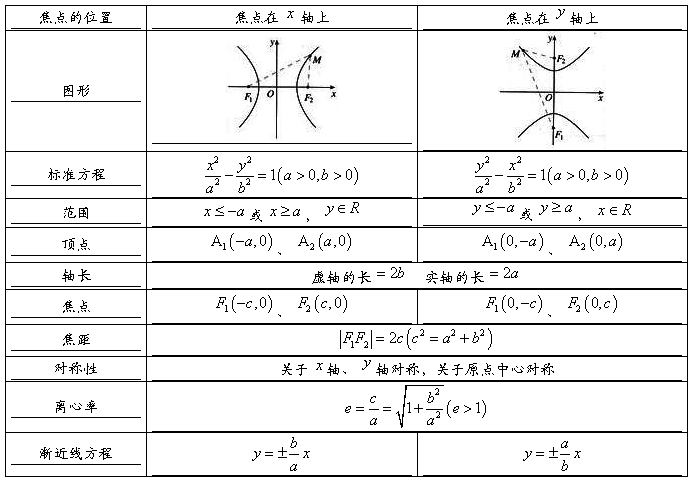
5、实轴和虚轴等长的双曲线称为等轴双曲线.
6、平面内与一个定点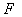 和一条定直线
和一条定直线 的距离相等的点的轨迹称为抛物线.定点
的距离相等的点的轨迹称为抛物线.定点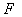 称为抛物线的焦点,定直线
称为抛物线的焦点,定直线 称为抛物线的准线.
称为抛物线的准线.
7、过抛物线的焦点作垂直于对称轴且交抛物线于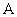 、
、 两点的线段
两点的线段 ,称为抛物线的“通径”,即
,称为抛物线的“通径”,即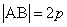 .
.
8、焦半径公式:
若点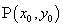 在抛物线
在抛物线 上,焦点为
上,焦点为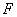 ,则
,则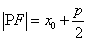 ;
;
若点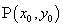 在抛物线
在抛物线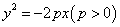 上,焦点为
上,焦点为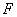 ,则
,则 ;
;
若点 在抛物线
在抛物线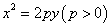 上,焦点为
上,焦点为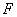 ,则
,则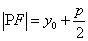 ;
;
若点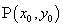 在抛物线
在抛物线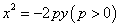 上,焦点为
上,焦点为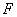 ,则
,则 .
.
9、抛物线的几何性质:

解题注意点:
1、“回归定义” 是一种重要的解题策略。如:
(1)在求轨迹时,若所求的轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的方程,写出所求的轨迹方程;(2)涉及椭圆、双曲线上的点与两个焦点构成的焦点三角形问题时,常用定义结合解三角形(一般是余弦定理)的知识来解决;(3)在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形利用几何意义去解决。
2、直线与圆锥曲线的位置关系
(1)有关直线与圆锥曲线的公共点的个数问题,直线与圆锥曲线的位置关系有三种情况:相交、相切、相离.联立直线与圆锥曲线方程,经过消元得到一个一元二次方程(注意在和双曲线和抛物线方程联立时二次项系数是否为0),直线和圆锥曲线相交、相切、相离的充分必要条件分别是 、
、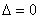 、
、 .
.
应注意数形结合(例如双曲线中,利用直线斜率与渐近线的斜率之间的关系考查直线与双曲线的位置关系)
常见方法:①联立直线与圆锥曲线方程,利用韦达定理等;
②点差法
(主要适用中点问题,设而不求,注意需检验,化简依据: )
)
(2)有关弦长问题,应注意运用弦长公式及韦达定理来解决;(注意斜率是否存在)
① 直线具有斜率 ,两个交点坐标分别为
,两个交点坐标分别为

② 直线斜率不存在,则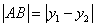 .
.
(3)有关对称垂直问题,要注意运用斜率关系及韦达定理,设而不求,简化运算。
考查三个方面:A 存在性(相交);B 中点;C 垂直(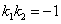 )
)
注: 1.圆锥曲线,一要重视定义,这是学好圆锥曲线最重要的思想方法,二要数形结合,既熟练掌握方程组理论,又关注图形的几何性质,以简化运算。
2.当涉及到弦的中点时,通常有两种处理方法:一是韦达定理;二是点差法.
3.圆锥曲线中参数取值范围问题通常从两个途径思考:一是建立函数,用求值域的方法求范围;二是建立不等式,通过解不等式求范围。
4.注意向量在解析几何中的应用(数量积解决垂直、距离、夹角等)
(4)求曲线轨迹常见做法:定义法、直接法(步骤:建—设—现(限)—代—化)、代入法(利用动点与已知轨迹上动点之间的关系)、点差法(适用求弦中点轨迹)、参数法、交轨法等。
例1.已知定点 ,在满足下列条件的平面上动点P的轨迹中是椭圆的是(答:C);
,在满足下列条件的平面上动点P的轨迹中是椭圆的是(答:C);
A.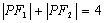 B.
B.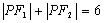 C.
C.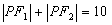 D.
D.
例2已知双曲线的离心率为2,F1、F2是左右焦点,P为双曲线上一点,且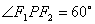 ,
,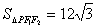 .求该双曲线的标准方程(答:
.求该双曲线的标准方程(答: )
)
例3 已知椭圆的一个顶点为A(0,-1),焦点在x轴上,若由焦点到直线的距离为3.
(1)求椭圆分方程;(2)设椭圆与直线相交于不同的两点M,N,当|AM|=|AN|时,求m的取值范围。(答: )
)
例4过点A(2,1)的直线与双曲线 相交于两点P1、P2,求线段P1P2中点的轨迹方程。
相交于两点P1、P2,求线段P1P2中点的轨迹方程。
第三章空间向量与立体几何
1、空间向量及其运算设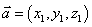 ,
,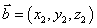 ,则
,则
 .
.
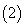
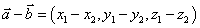 .
.
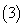
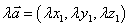 .
.
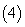
 .
.
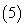 若
若 、
、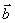 为非零向量,则
为非零向量,则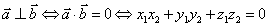 .
.
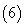 若
若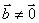 ,则
,则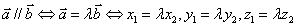 .
.

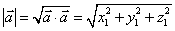 .
.
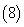
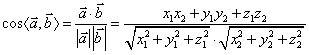 .
.
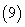
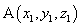 ,
,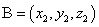 ,则
,则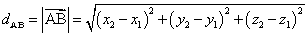 .
.
(10)共面向量定理: ;
;
P、A、B、C四点共面 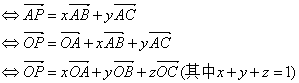
(11)空间向量基本定理 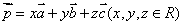 (不共面的三个向量
(不共面的三个向量 构成一组基
构成一组基
底,任意两个向量都共面)
2、平行:(直线的方向向量,平面的法向量)( 是a,b的方向向量,
是a,b的方向向量, 是平面
是平面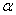 的法向量)
的法向量)
线线平行: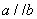


线面平行: 或
或  ,
,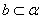 或
或  是
是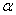 内不共线向量)
内不共线向量)
面面平行: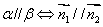
3、垂直
线线垂直: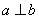


线面垂直: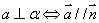 或
或  是
是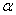 内不共线向量)
内不共线向量)
面面垂直: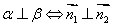
4、夹角问题
线线角 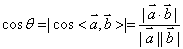 (注意异面直线夹角范围
(注意异面直线夹角范围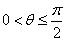 )
)
线面角 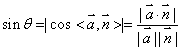
二面角  (一般步骤①求平面的法向量;②计算法向量夹角;③回答二面角(空间想象二面角为锐角还是钝角或借助于法向量的方向),只需说明二面角大小,无需说明理由))
(一般步骤①求平面的法向量;②计算法向量夹角;③回答二面角(空间想象二面角为锐角还是钝角或借助于法向量的方向),只需说明二面角大小,无需说明理由))
1. 距离问题(一般是求点面距离,线面距离,面面距离转化为点到面的距离)
P到平面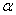 的距离
的距离 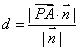 (其中
(其中 是平面
是平面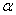 内任一点,
内任一点, 为平面
为平面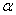 的法向量)
的法向量)
2. 立体几何解题一般步骤
坐标法:①建系(选择两两垂直的直线,借助于已有的垂直关系构造);②写点坐标;③写向量的坐标;④向量运算;⑤将向量形式的结果转化为最终结果。
基底法:①选择一组基底(一般是共起点的三个向量);②将向量用基底表示;③向量运算;④将向量形式的结果转化为最终结果。
几何法:作、证、求
异面直线夹角——平移直线(借助中位线平行四边形等平行线);
线面角——找准面的垂线,借助直角三角形的知识解决;
二面角——定义法作二面角,三垂线定理作二面角;作交线的垂面.
-
高中数学选修2-1知识点总结
高二数学选修21知识点1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句2若p则q形式的命题…
-
高二数学(理科)选修2-1知识点总结
高二数学归纳材料实小校区TEL87530008高二数学选修21知识点归纳资料第一部分简单逻辑用语1命题用语言符号或式子表达的可以判…
-
高二数学选修2-1知识点总结
高二数学上期末复习部分知识点概要20xx15高二数学选修21知识点1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的…
-
高中数学选修2-2知识点总结(精华版)
数学选修22知识点总结一导数1函数的平均变化率为fx2fx1fx1xfx1yfxxx2x1x注1其中x是自变量的改变量可正可负可零…
-
高中数学选修2-1、2-2知识点小结
选修2122知识点选修21第一章常用逻辑用语1命题及其关系四种命题相互间关系逆否命题同真同假2充分条件与必要条件p是q的充要条件p…
-
高中数学人教版选修2-2导数及其应用知识点总结
数学选修2-2导数及其应用知识点必记1.函数的平均变化率是什么?答:平均变化率为f(x2)?f(x1)f(x1??x)?f(x1)…
-
高中数学选修2-2知识点总结
导数及其应用一.导数概念的引入数学选修2-2知识点总结1.导数的物理意义:瞬时速率。一般的,函数y?f(x)在x?x0处的瞬时变化…
-
人教版高中数学选修1-1知识点总结(全)
高中数学选修11知识点总结第一章简单逻辑用语命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句…
-
高中数学选修2-1知识点总结
高二数学选修21知识点1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句2若p则q形式的命题…
-
人教版高中数学选修2-1知识点小结
选修21知识点选修21第一章常用逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句2…
-
高中数学选修2-2知识点总结
导数及其应用一.导数概念的引入数学选修2-2知识点总结1.导数的物理意义:瞬时速率。一般的,函数y?f(x)在x?x0处的瞬时变化…