二次函数图象和性质教案
羊安中学导学案

第二篇:二次函数的图象和性质教案
二次函数的图象和性质
峰
一、考点扫描
1、理解二次函数的概念:y=ax2+bx+c(a,b,c是常数,a≠0)
2、会把二次函数的一般式化为顶点式,确定图象的顶点坐标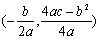 、对称轴
、对称轴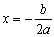 和开口方向,会用描点法画二次函数的图象;
和开口方向,会用描点法画二次函数的图象;
3、会平移二次函数y=ax2(a≠0)的图象得到二次函数y=a(x+k)2+h的图象,了解特殊与一般相互联系和转化的思想;
4、会用待定系数法求二次函数的解析式;
5、利用二次函数的图象,了解二次函数的增减性,会求二次函数的图象与x轴的交点坐标和函数的最大值、最小值,了解二次函数与一元二次方程和不等式之间的联系。
二、知识网络
1、二次函数
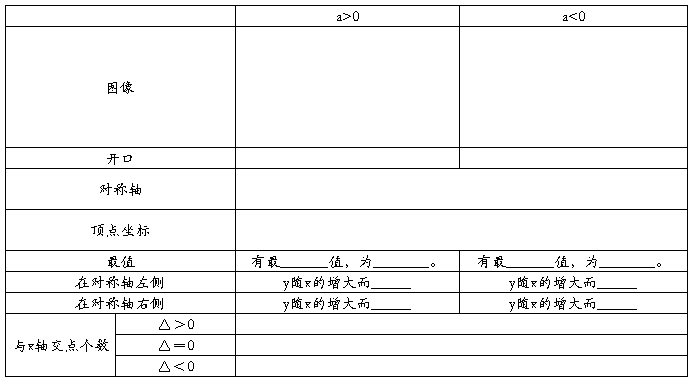
2、顶点式:y=_______________________,顶点坐标为_____________.
3、图象平移口诀:_______________________________________。
三、典型例题讲解
例1、已知某二次函数,当x=4时有最小值-3且它的图象与x轴交点的横坐标为1,
求:(1)它的函数解析式。;
(2)写出它的开口方向、对称轴方程和顶点坐标。;
(3)这个函数有最大值还是最小值?这个最值是多少?
分析:此题关键在于理解顶点坐标与函数最值之间的关系。
例2、已知开口向上的抛物线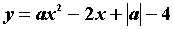 经过点(0,—2),
经过点(0,—2),
(1)、确定抛物线的解析式;
(2)、将该二次函数图象向右平移几个单位,可使得平移后的图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标
分析:本题解决(2)有两种思路:1、利用图象 2、设平移后的解析式为
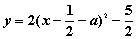 ,平移后过(0,0)代入确定a的值即可。
,平移后过(0,0)代入确定a的值即可。
例3、二次函数 的图象如图9所示,根据图象解答下列问题:
的图象如图9所示,根据图象解答下列问题:
(1)写出方程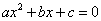 的两个根.
的两个根.
(2)写出不等式 的解集.
的解集.
(3)写出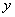 随
随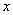 的增大而减小的自变量
的增大而减小的自变量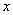 的取值范围.
的取值范围.
(4)若方程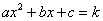 有两个不相等的实数根,求
有两个不相等的实数根,求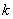 的取值范围.
的取值范围.
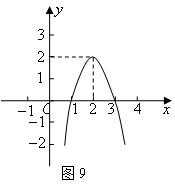 点评:本题主要考查数形结合的思想及识图能力
点评:本题主要考查数形结合的思想及识图能力
四、知识巩固与提高
1、二次函数y=-(x-1)2+3图像的顶点坐标是 ( )
A.(-1,3) B.(1,3) C.(-1,-3) D.(1,-3)
2、抛物线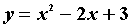 的对称轴直线是 ( )
的对称轴直线是 ( )
A、x=-2 B、x=2 C、x=-1 D、x=1
3、二次函数y=x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
A.y=x2+3 B. y=x2-3 C. y=(x+3)2 D. y=(x-3)2
4对于二次函数 ,我们把使函数值等于0的实数x叫做这个函数的零点。则二次函数
,我们把使函数值等于0的实数x叫做这个函数的零点。则二次函数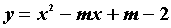 (m为实数)的零点的个数是 ( )
(m为实数)的零点的个数是 ( )
A.0 B.1 C.2 D.不能确定
5、一个运动员打高尔夫球,若球的飞行高度y(m)与水平距离x(m)之间的函数表达式为 ,则高尔夫球在飞行过程中的最大高度为
,则高尔夫球在飞行过程中的最大高度为
( )
A、10m B、20m C、30m D、60m
6、小明、小亮、小虎、小燕四人共同探究代数式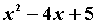 的值的情况,他们作了如下分工:小明负责找值为1时的x值,小亮负责找值为0时x的值,小虎负责找最小值;小燕负责找最大值。几分钟后,各自通报探究的结论,其中错误的是 ( )
的值的情况,他们作了如下分工:小明负责找值为1时的x值,小亮负责找值为0时x的值,小虎负责找最小值;小燕负责找最大值。几分钟后,各自通报探究的结论,其中错误的是 ( )
A、小明认为只有当x=2时,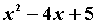 的值为1
的值为1
B、小亮认为找不到实数x,使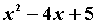 的值为0;
的值为0;
C、小虎发现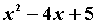 的值随x的变化而变化,因此认为没有最小值;
的值随x的变化而变化,因此认为没有最小值;
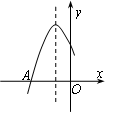 D、小燕发现当x取大于2的实数时,
D、小燕发现当x取大于2的实数时,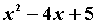 的值随x的增大而增大,因此认为没有最大值。
的值随x的增大而增大,因此认为没有最大值。
7、如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是( ).B
(A)②④ (B)①④ (C)②③
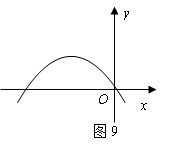 8、如图9所示的抛物线是二次函数
8、如图9所示的抛物线是二次函数 的图象,那么
的图象,那么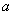 的值是 .
的值是 .
9、已知二次函数的图象开口向上,且对称轴在y轴的
右侧,请你写出一个满足条件的二次函数的解析式_________________________________。
10、将抛物线y=2x2先沿x轴方向向左平移2个单位,再沿y轴方向向下平移3个单位,所得抛物线的解析式是_________________。
11、飞机着陆后滑行的距离s(单位:米)与滑行时间t(单位:秒)之间的函数关系式是s=60t-1.5t2.飞机着陆后滑行__________秒才能停下来。
12、二次函数 的部分对应值如下表:
的部分对应值如下表:

二次函数 图象的对称轴为x=__________;x=2对应的函数值y=_____________。
图象的对称轴为x=__________;x=2对应的函数值y=_____________。
 13、已知二次函数图象的顶点是
13、已知二次函数图象的顶点是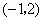 ,且过点
,且过点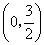 .
.
(1)求二次函数的表达式,并在图10中画出它的图象;
(2)求证:对任意实数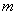 ,点
,点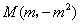 都不在这个
都不在这个
二次函数的图象上.
,
 14、如图13,已知二次函数
14、如图13,已知二次函数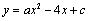 的图像经过点A和点B.
的图像经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
15、阅读材料,解答问题.
当抛物线的表达式中含有字母系数时,随着系数中的字母取值的不同,抛物线的顶点坐标出将发生变化.例如y=x2-2mx+m2+2m-1①,有y=(x-m)2+2m-1②,∴抛物线的顶点坐标为(m,2m-1),即
当m的值变化时,x、y的值也随之变化,因而y值也随x值的变化而变化.
把③代入④,得y=2x-1.⑤
可见,不论m取任何实数,抛物线顶点的纵坐标y和横坐标x都满足表达式y=2x-1.
解答问题:
(1)在上述过程中,由①到②所学的数学方法是 ,其中运用了 公式,由③、④到⑤所用到的数学方法是 .
(2)根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-3m+1顶点的纵坐标y与横坐标x之间的表达式.
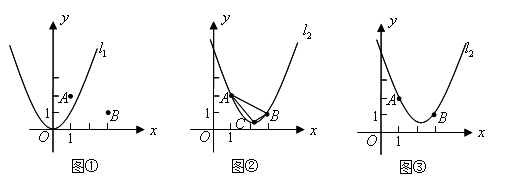
16、(2007山东威海)如图①,在平面直角坐标系中,点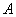 的坐标为
的坐标为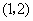 ,点
,点 的坐标为
的坐标为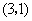 ,二次函数
,二次函数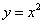 的图象记为抛物线
的图象记为抛物线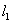 .
.
(1)平移抛物线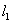 ,使平移后的抛物线过点
,使平移后的抛物线过点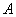 ,但不过点
,但不过点 ,写出平移后的一个抛物线的函数表达式: (任写一个即可).
,写出平移后的一个抛物线的函数表达式: (任写一个即可).
(2)平移抛物线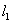 ,使平移后的抛物线过
,使平移后的抛物线过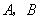 两点,记为抛物线
两点,记为抛物线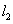 ,如图②,求抛物线
,如图②,求抛物线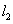 的函数表达式.
的函数表达式.
(3)设抛物线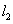 的顶点为
的顶点为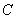 ,
, 为
为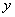 轴上一点.若
轴上一点.若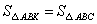 ,求点
,求点 的坐标.
的坐标.
(4)请在图③上用尺规作图的方式探究抛物线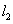 上是否存在点
上是否存在点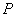 ,使
,使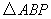 为等腰三角形.若存在,请判断点
为等腰三角形.若存在,请判断点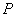 共有几个可能的位置(保留作图痕迹);若不存在,请说明师.
共有几个可能的位置(保留作图痕迹);若不存在,请说明师.
-
二次函数教学反思
二次函数教学反思从课本的体系来看这节课明显是要让学生明白什么是二次函数能区别二次函数与其他函数的不同能深刻理解二次函数的一般形式并…
-
二次函数教学反思2
二次函数教学反思在二次函数教学中根据它在初中数学函数在教学中的地位细心地准备二次函数的教学教学重点为二次函数的图象性质及应用教学难…
-
二次函数教学反思
二次函数单元教学反思第二十六章二次函数是学生学习了正比例函数一次函数和反比例函数以后进一步学习函数知识是函数知识螺旋发展的一个重要…
-
二次函数的图象与性质教学反思
2y?ax?c的图象与性质的教学反思二次函数这节课是青岛版九年级数学下册的一节探究课。在教学中我采用了体验探究的教学方式,在教师的…
-
《26.1二次函数》教学反思
261二次函数教学反思龙潭镇第一初级中学黄海东这节课是安排在学了一次函数反比例一元二次方程之后的二次函数的第一节课学习目标是要学生…
-
20xx区划地名工作总结
20xx年区划地名工作总结今年我市区划地名工作在省民政厅和局领导的关心重视下,按照年初工作计划,以学习实践科学发展观为主线,立足区…
-
00劳动合同续签工作总结
劳动合同续签工作总结转眼间我已经来到xx整整一年了,从去年的3月底入职以来,在公司领导和全体同事的关怀、帮助、支持下,紧紧围绕中心…
-
应用写作学习总结
20xx-20xx年第一学期《应用写作》科目考查卷专业:英语(涉外文秘)班级:涉外11-1任课教师:姓名:学号:111340101…
-
小班教研工作总结
生命不息,学习不止!在本学期的教研中,收获颇多,无论是全体教师教研,还是小班组教研,还是本班教研,都为大家搭建了平台,分享自己的成…
-
两节两会食品药品总结
20xx年两会两节期间餐饮服务食品安全及药品安全工作的总结根据**市食品药品监督管理局巴南区分局《关于加强20xx年两会两节期间餐…