数学分析习作读书报告2
云 南 大 学
数学分析习作课(2)读书报告
题 目: 隐函数的偏导数
学 院: 数学与统计学院
专 业: 数学与应用数学
姓名、学号: 章豪 20121910030
任课教师: 黄辉
时 间: 20##-06-05-星期三
摘 要:上学期接触了隐函数的求导方法,这学期接触了偏导数,虽然对隐函数的存在定理、函数相关也有介绍,但是没有对它的偏导数的求法没有做具体相关介绍,现在就对隐函数的偏导数的求法进行一些讨论和总结。
关键词:隐函数、偏导数(一阶,二阶)、微分。
一、隐函数的一阶偏导数的求法
㈠由一个方程确定的一个隐函数,其一阶偏导数的求法。
设由方程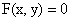 确定一个隐函数
确定一个隐函数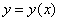 ,则
,则
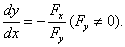
设由方程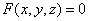 确定一个二元隐函数
确定一个二元隐函数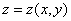 ,求这函数的偏导数有如下几种方法。
,求这函数的偏导数有如下几种方法。
法一 直接求导法
把 ,
, 看作独立变量,
看作独立变量,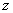 是
是 、
、 的函数。在方程
的函数。在方程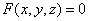 两边分别
两边分别 ,
, 求导,得到含
求导,得到含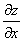 、
、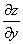 的两个方程,然后解出所求的导数。
的两个方程,然后解出所求的导数。
例1 函数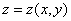 是由方程
是由方程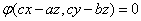 确定的隐函数,其中
确定的隐函数,其中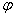 是可微函数,
是可微函数,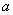 ,
,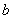 ,
,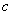 是常数,且
是常数,且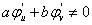 ,求
,求 ,并指出曲面
,并指出曲面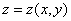 是什么曲面?
是什么曲面?
解 为求方程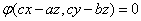 所确定的二元隐函数
所确定的二元隐函数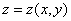 的两个偏导数
的两个偏导数 、
、 ,在该方程两边分别对
,在该方程两边分别对 、
、 求偏导,得到
求偏导,得到
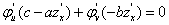 ,
,
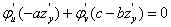 ,
,
解之分别得到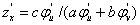 ,
,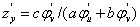 。
。
则 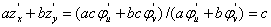 。
。
即  ,亦即
,亦即
 ,
,
其中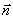 为曲面方程
为曲面方程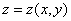 所表示的空间曲面上的任一点处的法向量
所表示的空间曲面上的任一点处的法向量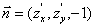 。上式表明,该法向量
。上式表明,该法向量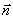 与一个常向量
与一个常向量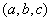 垂直,这说明曲面上任一点的切平面和
垂直,这说明曲面上任一点的切平面和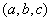 平行,故曲面是一个其母线平行于
平行,故曲面是一个其母线平行于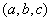 的柱面。
的柱面。
法二 结合使用多元复合函数求导法则与函数四则运算求导法则求之。
例2 设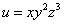 ①,若
①,若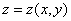 是由方程
是由方程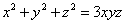 ②所确定的隐函数,求
②所确定的隐函数,求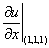 。
。
解 在①式两边对 求导,注意
求导,注意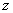 是
是 ,
, 的函数,有
的函数,有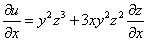 ③
③
再在②式两边对 求导,得到
求导,得到
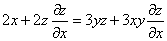 ,即
,即 ④
④
将④式代入③式即得
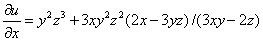 ,
,
故  。
。
法三 公式法
设由方程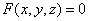 确定隐函数
确定隐函数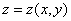 ,且
,且 ,则
,则
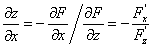 ,
, ①
①
注意:利用上两式求隐函数的偏导数时,要注意三点。一是先要将所给等式化成方程
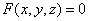 的形式;二是求
的形式;二是求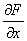 时,视
时,视 ,
,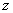 为常数;求
为常数;求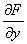 时,视
时,视 ,
,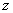 为常数;求
为常数;求 时,视
时,视 ,
, 为常数;三是①式中左端的负号不要漏掉。
为常数;三是①式中左端的负号不要漏掉。
所确定的隐函数在方程中出现二次时,可用①式求其偏导数。
例3 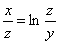 确定函数
确定函数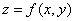 ,求
,求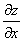 ,
,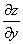 。
。
解 先将原方程改写成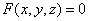 的形式:
的形式:
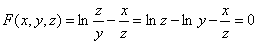 .
.
在上面的方程中隐函数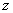 出现二次,可用①式求其偏导数,将
出现二次,可用①式求其偏导数,将
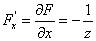 (视
(视 ,
,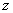 为常量);
为常量);
 (视
(视 ,
,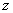 为常量)=
为常量)= ;
;
 (视
(视 ,
, 为常量)
为常量)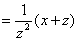 ,
,
代入①式得到
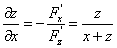 ;
; 。
。
例4 设 ,
,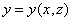 ,
,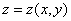 都是由
都是由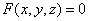 所确定的具有连续偏导数的函数,证明
所确定的具有连续偏导数的函数,证明
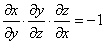
证 因 是由
是由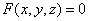 所确定的隐函数,有
所确定的隐函数,有
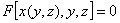 ,
,
则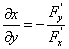 ,同理可得
,同理可得
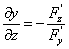 ,
,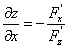
故有 
注意:由上例看出偏导数记号是一个整体记号,不能理解为分子和分母的商,这一点也是与一元函数的导数(可看成分子与分母上的微分的商)不相同的地方!
法四 利用全微分形式不变性求之。
在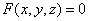 两边求全微分得
两边求全微分得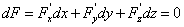 ,从而得到
,从而得到
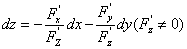 ,
,
又 ,于是有
,于是有 ,
,
这就是说,由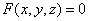 求出函数
求出函数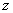 的全微分
的全微分 的表示式,其中
的表示式,其中 ,
,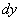 前面的系数即为所求的偏导数
前面的系数即为所求的偏导数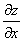 ,
,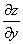 。
。
总结:对于那些变量之间关系比较复杂的函数,常利用全微分法求出其所有偏导数。这是因为利用全微分法,在逐步作微分运算的过程中,不论变量之间的关系如何错综复杂,可以不必对它们进行辨认和区分,而一律作为自变量处理,从而给求解函数的偏导数带来很大方便。又由于微分运算所得结果对自变量的微元 ,
,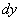 ,...来说都是线性的,稍作整理即可同时求出所有一阶偏导数,而且也不易出错。因此需同时求隐函数的各个偏导数或证明隐函数的各个偏导数都出现的等式常用全微分法求之或证之。
,...来说都是线性的,稍作整理即可同时求出所有一阶偏导数,而且也不易出错。因此需同时求隐函数的各个偏导数或证明隐函数的各个偏导数都出现的等式常用全微分法求之或证之。
例5 已知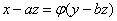 ,试证
,试证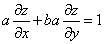 .
.
证明1 题意知由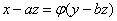 确定
确定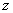 是
是 ,
, 的函数。又在待证的等式中需同时求出
的函数。又在待证的等式中需同时求出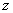 的两个偏导数,可用全微分形式不变性求之,然后证其满足待证的关系。
的两个偏导数,可用全微分形式不变性求之,然后证其满足待证的关系。
 ,
,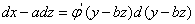 ,
,
 ,
,
 ,
,
故 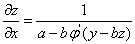 ,
,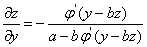 .
.
因而  .
.
证明2 注意到隐函数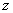 在所给等式两端同时出现,也可用
在所给等式两端同时出现,也可用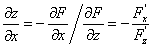 ,
, 证之。为此令
证之。为此令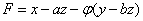 ,
, ,则
,则
 ,
, ,
,
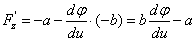 ,
,
故 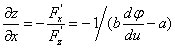 ,
, .
.
因而 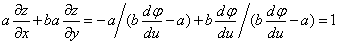 .
.
㈡由方程组确定的隐函数,其一阶偏导数的求法
求法一 解方程组法
求解这类隐函数的偏导数,首先要根据题设条件,搞清楚有几个隐函数,是几元的隐函数,以及哪些变量是因变量、自变量。把这些关系搞清楚后,在有关方程两边分别对自变量求导,通过解联立方程组求出所求的偏导数。
例6 求出方程组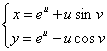 所确定的隐函数的偏导数
所确定的隐函数的偏导数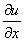 ,
, ,
, ,
,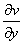 .
.
解 由所求偏导数表明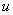 ,
,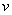 为因变量。这里两个方程一共包含四个变量,只能确定两个隐函数
为因变量。这里两个方程一共包含四个变量,只能确定两个隐函数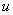 ,
,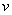 ,故
,故
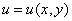 ,
,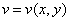 .
.
在原方程组的两个方程两边分别对 求偏导数,得到
求偏导数,得到
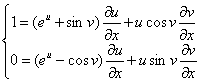
用克莱姆法则解上述方程组得到
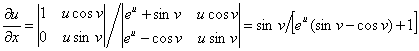

同法可求得
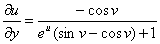 ,
,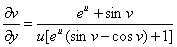
注意: 一般地,由 个
个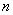 元方程构成的方程组(隐函数组)
元方程构成的方程组(隐函数组)

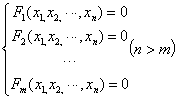
中所含方程个数就是所含隐函数的个数,方程组中所出现的变量的个数减去方程的个数就是自变量的个数。因而在一定条件下此方程组可确定 个
个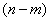 元的单值函数:
元的单值函数:
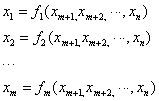
将隐函数组各方程分别对自变量求偏导数,再解所得的线性方程(组),即可求得隐函数的偏导数。
求法二 全微分法
由方程组确定的隐函数,各变量之间的关系比较复杂,难以区分变量的性质,也可以利用全微分形式不变性先求全微分,再按题意求出所有的偏导数。其运算比较简便,且一次同时可求得所有一阶偏导数。
例7 求由方程组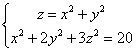 所确定的隐函数导数
所确定的隐函数导数 ,
,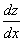 .
.
解 对所给的方程组求全微分得到
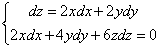
由题意知 、
、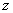 是因变量,
是因变量, 为自变量。把因变量的微分放在等式左端,自变量的微分放在等式右端,上式变式为
为自变量。把因变量的微分放在等式左端,自变量的微分放在等式右端,上式变式为

解得 
即 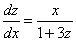
同法可求得 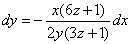 ,即
,即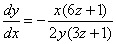
求法三 显化法
如能由给定的方程组解出函数的显式,则可对此显式直接求出所求的偏导数。
例8 设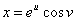 ①,
①,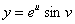 ②,
②,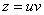 ③,求
③,求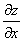 ,
,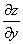 .
.
解 用显化法求之,为此先求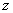 用
用 、
、 表示的式子
表示的式子
由①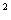
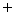 ②
②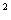 得到
得到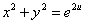 ,取对数有
,取对数有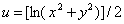
②/①得到 
 ,即
,即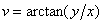
因而 
上式两边对 求导得到
求导得到


二、隐函数的二阶偏导数的求法
一般用两种方法求之。一是直接对原方程接连两次求偏导;二是先求出一阶偏导数的表达式,再对其求一次偏导。但在求指定点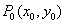 处的二阶偏导数的值时,常采用前一种方法,即对原方程两次求导,不需解出一阶偏导数的表达式,只求出其在
处的二阶偏导数的值时,常采用前一种方法,即对原方程两次求导,不需解出一阶偏导数的表达式,只求出其在 处的值,代入含二阶导数的式子,即可求出二阶偏导数在
处的值,代入含二阶导数的式子,即可求出二阶偏导数在 处的值。这样计算较简便。
处的值。这样计算较简便。
例9 求下列方程所确定的隐函数的指定阶导数:
⑴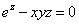 ,
,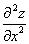 ;⑵
;⑵ ,
,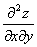 .
.
解 ⑴将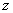 视为
视为 ,
, 的隐函数
的隐函数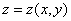 ,在所给方程两边对
,在所给方程两边对 求偏导数得到
求偏导数得到
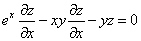 ①,解之得
①,解之得 ②
②
在上述方程①的两边再对 求导,得到
求导,得到
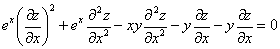 ③
③
将②式代入③式,并解出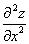 得到
得到

⑵在所给方程两端对 求导得到
求导得到
 ,解之得到
,解之得到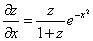 . ④
. ④
注意到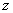 是
是 的函数,在④式两边对
的函数,在④式两边对 求偏导数得到
求偏导数得到
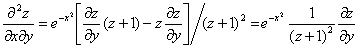 ⑤
⑤
为求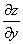 ,在所给方程两端对
,在所给方程两端对 求导得到
求导得到
 ,解之得到
,解之得到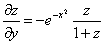
将其代入⑤式得到
 .
.
例10 设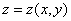 是由方程
是由方程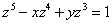 确定的隐函数,求
确定的隐函数,求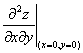
解 在原方程两边对 ,
, 求偏导,分别得到
求偏导,分别得到
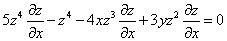 ,①
,①
 ②
②
在①式两边对 求偏导,得到
求偏导,得到

将 ,
,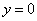 代入原方程得到
代入原方程得到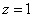 。将
。将 ,
,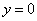 ,
,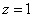 代入①式、②式分别有
代入①式、②式分别有
 ,
,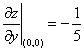 .
.
将一阶偏导数之值及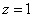 代入③式得到
代入③式得到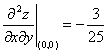 .
.
参考文献
[1] 数学分析内容、方法与技巧(下),孙清华 孙昊等编著,华中科技大学出版社,2005.
[2]数学分析题解精粹第二版,钱吉林等编著 忠邦考试教育研究所 策划,湖北长江出版集团,2009.
[3]高等数学解题方法技巧归纳(下), 毛纲源,华中科技大学出版社,2002.
-
数学读书报告
数学建模读书报告读数学中的美吴振奎吴旻著五月中旬我阅读了吴振奎吴旻两位先生所著的数学中的美一书书中从简洁和谐奇异三个方面记述了数学…
-
数学读书报告
数学读书报告中国数学简史姓名刘晓玥班级人管1031班学号1021053126数学我以前并不怎么喜欢它直到数学老师让我们看关于数学的…
-
数学读书报告
数学读书报告看完了一本书,名叫《数学与艺术——无穷的碎片》.这本书包含了十个章节,参考文献以及索引三大部分,是我从未见过的创新.这…
-
数学思维教育读书报告
摘要数学与思维读书报告摘要众所周知数学是人类文明的一个重要组成部分也是几千年来人类智慧的结晶数学思维除了具有概括性和间接性等特点外…
-
《数学与文化》读书报告
数学与文化读书报告通信工程学院专业一作者简介齐民友安徽芜湖人中国数学家19xx年加入中国共 产 党19xx年毕业于武汉大学数学系历…
-
数学读书报告
数学建模读书报告读数学中的美吴振奎吴旻著五月中旬我阅读了吴振奎吴旻两位先生所著的数学中的美一书书中从简洁和谐奇异三个方面记述了数学…
-
数学文化读书报告
数学与文化读书报告作者简介齐民友安徽芜湖人中国数学家19xx年毕业于武汉大学数学系历任武汉大学讲师教授数学研究所副所长研究生院院长…
-
数学文化读书报告
数学文化读书报告一数学是什么数学是什么正如科学是什么系统是什么精神是什么文化是什么生命是什么等问题一样都是众说纷纭的问题每个人都觉…
-
数学文化与思维—读书报告
数学文化与思维读书报告随着数字信息时代的进一步发展和深化科学技术正以前所未有的速度迅猛发展并且深刻影响着人类文明几乎所有领域而数学…
-
“大学文科数学”第二学期读书报告作业要求(20xx级)
20xx20xx学年第二学期学生读书报告作业内容及要求一内容要求可以从下列五个方面择一也可以参考数学之美中的选题1学习数学的心得和…