实验五  周期信号的傅里叶级数及频谱分析

5.1实验目的

１．学会运用MATLAB分析傅里叶级数展开，深入理解傅里叶级数的物理意义；

2．学会运用MATLAB分析周期信号的频谱特性。

5.２实验原理及实例分析

任何一个周期为T₁的正弦周期信号，只要满足狄利克利条件，就可以展开成傅里叶级数。

其中三角傅里叶级数为：

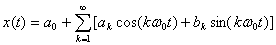                5.1

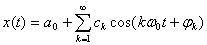或：                              5.2

其中，称为信号的基本频率（Fundamental frequency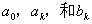），分别是信号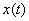的直流分量、余弦分量幅度和正弦分量幅度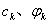，为合并同频率项之后各正弦谐波分量的幅度和初相位，它们都是频率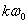的函数，绘制出它们与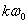之间的图像，称为信号的频谱图（简称“频谱”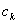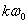），－图像为幅度谱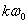，－图像为相位谱。

三角形式傅里叶级数表明，如果一个周期信号x(t)，满足狄里克利条件，那么，它就可以被看作是由很多不同频率的互为谐波关系（harmonically related）的正弦信号所组成，其中每一个不同频率的正弦信号称为正弦谐波分量(Sinusoid component)，其幅度（amplitude）为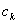。也可以反过来理解三角傅里叶级数：用无限多个正弦谐波分量可以合成一个任意的非正弦周期信号。

指数形式的傅里叶级数为：

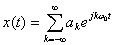                            52.3

其中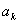，为指数形式的傅里叶级数的系数，按如下公式计算：

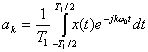                                            5.4

指数形式的傅里叶级数告诉我们，如果一个周期信号x(t)，满足狄里克利条件，那么，它就可以被看作是由很多不同频率的互为谐波关系（harmonically related）的周期复指数信号所组成，其中每一个不同频率的周期复指数信号称为基本频率分量，其复幅度（complex amplitude）为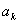。这里“复幅度（complex amplitude）”指的是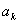通常是复数。

上面的傅里叶级数的合成式说明，我们可以用无穷多个不同频率的周期复指数信号来合成任意一个周期信号。然而，用计算机（或任何其它设备）合成一个周期信号，显然不可能做到用无限多个谐波来合成，只能取这些有限个谐波分量来近似合成。

假设谐波项数为N，则上面的和成式为：

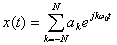                            5.5

显然，N越大，所选项数越多，有限项级数合成的结果越逼近原信号x(t)。本实验可以比较直观地了解傅里叶级数的物理意义，并观察到级数中各频率分量对波形的影响包括“Gibbs”现象：即信号在不连续点附近存在一个幅度大约为9%的过冲，且所选谐波次数越多，过冲点越向不连续点靠近。这一现象在观察周期矩形波信号和周期锯齿波信号时可以看得很清楚。

例题5-1：给定一个周期为T₁ = 2s的连续时间周期方波信号，如图所示，其一个周期内的数学表达式为：

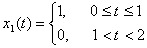
>> k = -10:10;

ak = ((-j).^k).* (sin((k+eps)*pi/2)./((k+eps)*pi))

ak =

  Columns 1 through 4

  -0.0000                  0 + 0.0354i  -0.0000                  0 + 0.0455i

  Columns 5 through 8

  -0.0000                  0 + 0.0637i  -0.0000                  0 + 0.1061i

  Columns 9 through 12

  -0.0000                  0 + 0.3183i   0.5000                  0 - 0.3183i

  Columns 13 through 16

  -0.0000                  0 - 0.1061i  -0.0000                  0 - 0.0637i

  Columns 17 through 20

  -0.0000                  0 - 0.0455i  -0.0000                  0 - 0.0354i

  Column 21

  -0.0000         

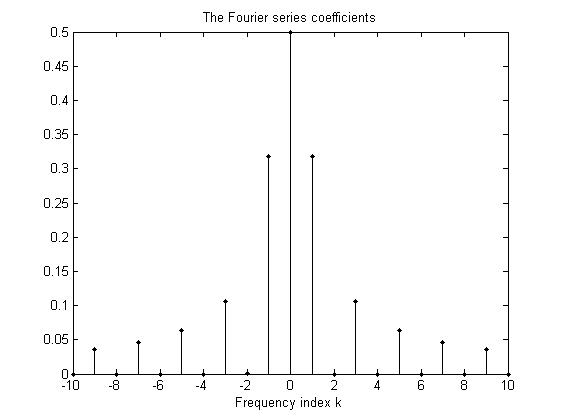
>>stem(k,abs(ak),'k.')

title('The Fourier series coefficients')

xlabel('Frequency index k')

5.3  编程练习

1. 周期三角脉冲信号如图4-1所示，求出其傅里叶级数，并用MATLAB频谱图，分析信号的频率特性。

 

>> k=-10:10;

ak=(1-cos(k*pi)) ./ (k*pi).^2

stem(k,abs(ak),'k.')

title('The Fourier series coefficients')

xlabel('Frequency index k')

ak =

  Columns 1 through 7

         0    0.0025         0    0.0041         0    0.0081         0

  Columns 8 through 14

    0.0225         0    0.2026       NaN    0.2026         0    0.0225

  Columns 15 through 21

         0    0.0081         0    0.0041         0    0.0025         0

 

第二篇：北航信号实验一信号分析实验报告

信号与测试实验一

一  实验目的

1.掌握基本信号的时域和频域分析方法。

2.掌握信号的自相关和互相关分析，了解其应用。 

二  实验原理

相关MATLAB函数

（1）信号产生函数

正弦：y=A*sin(2*pi*f*t)

方波：y=A*square(2*pi*f*t)

锯齿：y=A*sawtooth(2*pi*f*t)

随机噪声：y=A*randn(size(t))

（2）傅里叶变换及反变换

Y=fft(x,N)   x为信号，N为点数，是2的幂次。

（3）相关运算

c=xcorr(x，'unbiased')  求信号x的自相关，'unbiased'为无偏估计

c=xcorr(x,y,'unbiased')    信号x、y的互相关

（4）波形显示

plot(x,y)     x为横坐标，y为纵坐标

添加标注 xlabel(‘text’)    将text添加到x轴下方

ylabel(‘text’)    将text添加到y轴下方

title(‘text’)        将text添加到图形上方

三  实验步骤及内容

1     产生不同的周期信号，包括正弦信号、方波信号、锯齿波信号，在时域分析这些波形特征(幅值、频率(周期))。对产生的信号进行Fourier变换，在频域分析信号的特征，并说明方波信号和锯齿波信号的信号带宽（进行傅里叶变换时注意采样频率）。

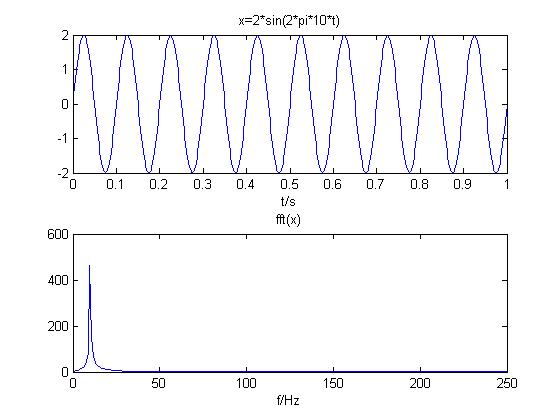
（1）正弦信号

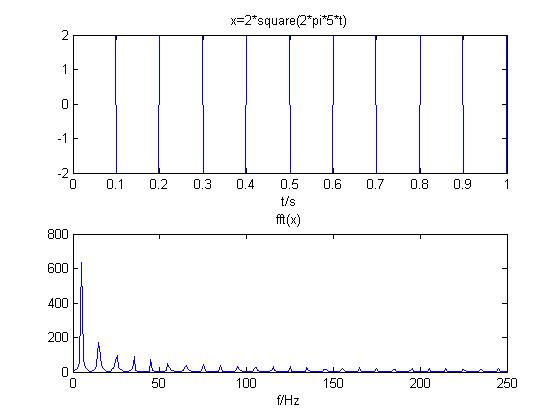
（2）方波信号

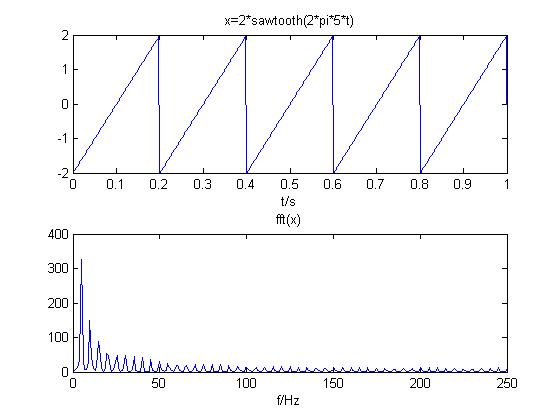
（3）锯齿波信号

时域

频域

正弦信号频谱离散，仅在f=10Hz时幅值最大；

方波信号频谱离散，在5Hz的奇数倍频有振幅值，且随着频率增大，振幅值减小，其他频率点振幅值为零，信号带宽50Hz；

锯齿波信号频谱离散，在5Hz的倍数频率处有振幅值，且随着频率增大，振幅值减小，其他频率点振幅值为零，信号带宽50HZ。

2 在Matlab中产生随机噪声、阶跃信号（选作）、矩形脉冲（选作）。对产生的信号进行Fourier变换，在频域分析信号的特征（进行傅里叶变换时注意采样频率）。

（1）    随机噪声

随机噪声的频谱为连续频谱，分布与幅值均随机。

3 产生复合信号：

           由3个不同频率、幅值的正弦信号叠加的信号，从图形上判断信号的特征；

               产生由正弦信号和随机信号叠加的混合信号，从图形上判断信号的特征；

               产生由正弦信号和方波叠加的信号，从图形上判断信号的特征。

对中的3种复合信号进行FFT计算，从图上判断信号的特征。

（1）3个正弦信号叠加

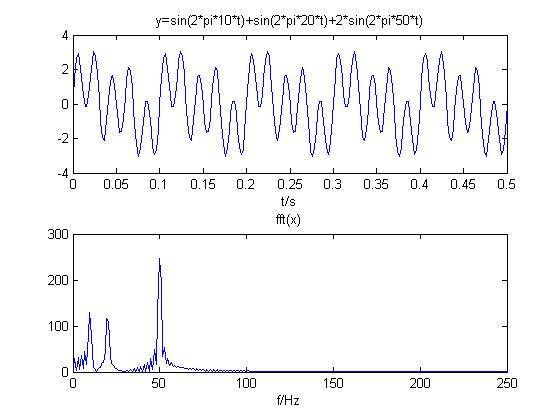
3个正弦信号叠加仍为周期信号，频谱离散，在10 Hz,20 Hz,50Hz处有振幅，且50 Hz信号振幅为两倍。

（2）    正弦叠加噪声信号

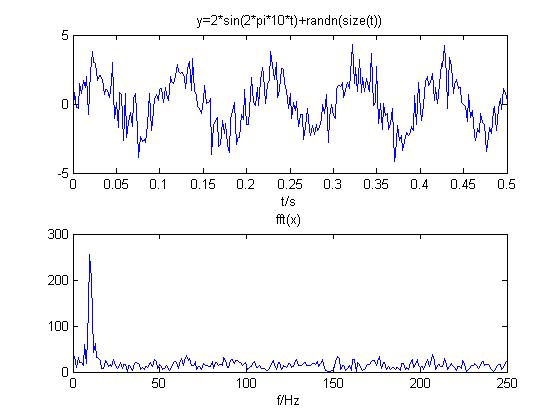
正弦信号与噪声信号叠加大致为正弦信号，但信号不光滑，其频谱离散，是正弦与噪声各自频谱的叠加，其中10Hz处幅值最大，其余部分幅值很小且随机。

（3）    正弦信号叠加方波信号

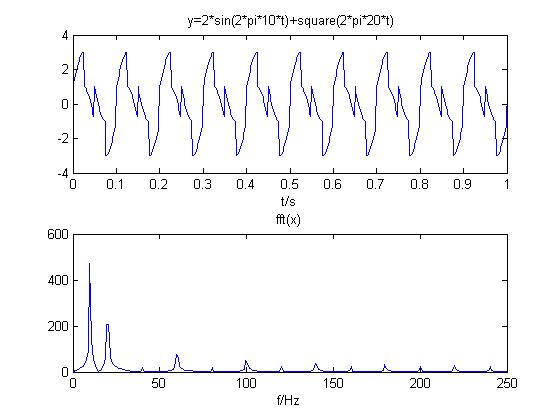
正弦信号与方波叠加仍为周期信号，频谱离散，在10Hz和20Hz的整数倍处有振幅，是正弦与方波各自频谱的叠加，在10Hz处振幅最大。

4产生一个基波信号，显示图形；按照方波的傅里叶级数展开的规律再叠加一个三次谐波，显示图形；再叠加一个五次谐波，显示图形，观察信号的变化。将以上图形显示在同一张图的不同部分。

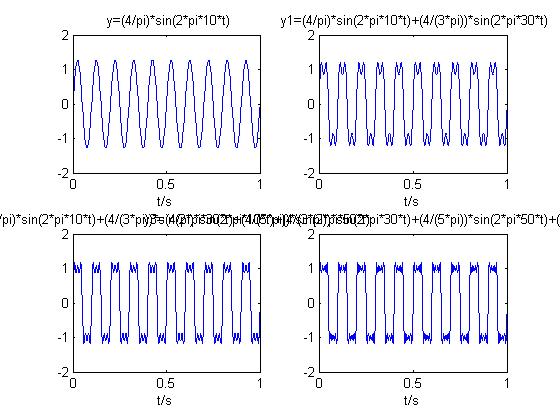
随着高次谐波的叠加，信号越来越接近方波，验证了其傅里叶展开。

5产生一个周期信号，进行自相关运算，说明周期信号进行自相关运算后的信号与原信号相比的特点。

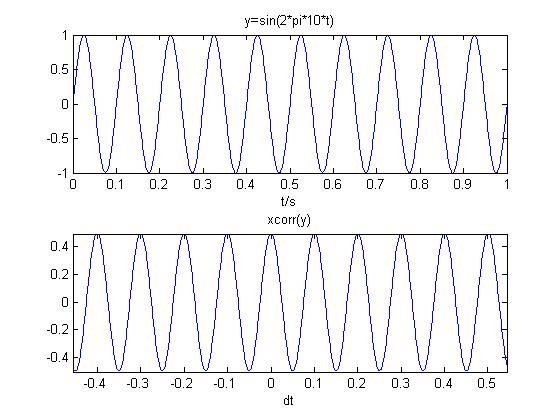
对于，自相关运算后为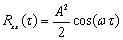，保留了振幅和频率的信息，丢失了相角信息。图中可以看出，自相关运算信号幅值为原信号一半，频率不变。

6对白噪声信号进行自相关运算，观察运算后信号特征，并叙述产生这种现象的原因。

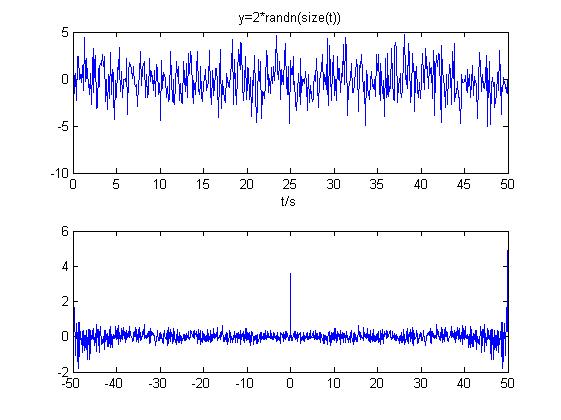
自相关函数为偶函数，在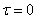处幅值最大，其他频率处振幅值几乎为零，随机信号在不等于0时没有相关性。

7 对5中产生的周期信号叠加白噪声，进行自相关运算，观察信号特征。

自相关函数仍是周期信号，相关分析后获得的波形去除了噪声影响，大致能看出原信号的频率和幅值等，因此，自相关分析可以用于带噪声信号的处理。

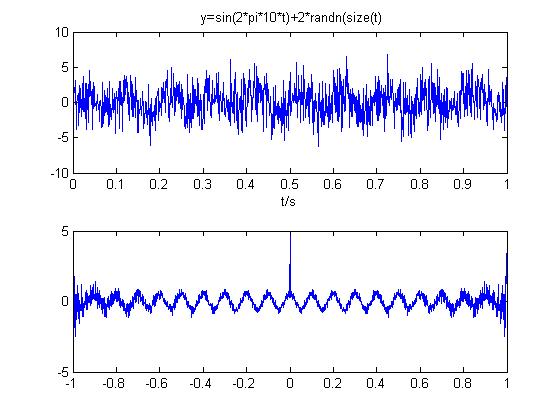
8产生两个同频率的周期信号，进行互相关运算，观察运算后的信号。

两个同频率周期信号互相关函数仍是周期函数，频率不变，幅值为原信号幅值乘积的一半，互相关函数能表明两个信号的相位差与相关性信息。

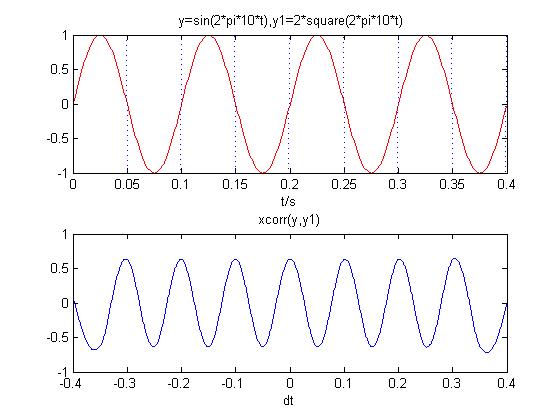
9 产生两个不同频率的周期信号，进行互相关运算，观察运算后的信号。

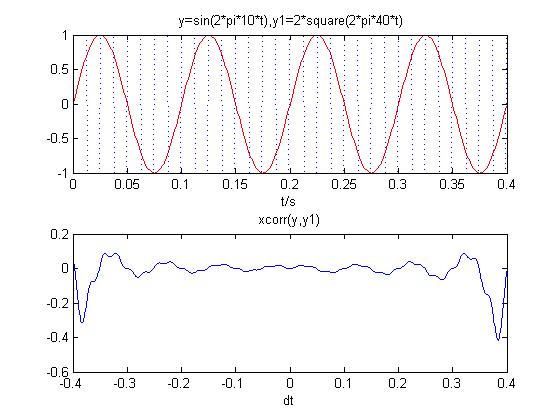
两个不同频率周期性信号互相关运算后幅值几乎为0，相关性较差。

四 实验意义

1.   傅里叶变换

傅里叶变换将信号的时域描述和频域描述建立起彼此一一对应的关系，其性质有助于我们理解信号的特征、运算和变化，为复杂问题的分析和简化提供帮助。因而傅里叶变换在工程实践与科学研究中有着重要的意义。

2  自相关和互相关函数

自相关函数表达了同一过程不同时刻的相互依赖关系，是信号与自身的延迟信号的乘积进行积分运算，对结果进行频谱分析可以获得原信号的周期幅值等信息，能从复合信号中分离出周期信号的信息。自相关函数常常应用于检测信号回声，检测淹没在随机噪声中的周期信号以及不同类型信号的辨识。

互相关函数表示不同过程的某一时刻的相互依赖关系，是信号与延迟后的另一信号的乘积进行积分运算，其结果保留了两个信号的同频分量的频率、幅值和相位差的信息。互相关函数常常应用于测速和测距，检测淹没在外来噪声中的信号以及系统脉冲响应的测定