20xx年四川高考文科数学试题和答案详解
绝密★启封并使用完毕前
20##年普通高等学校招生全国统一考试(四川卷)
数 学(文史类)
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)。第Ⅰ卷1至2页,第Ⅱ卷3至4页。满分l50
分。考试时间l20分钟。考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。考试结束后,将本试题卷和答题卡一并交回。
第Ⅰ卷(选择题共50分)
注意事项:
必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑。
第Ⅰ卷共10小题。
一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.设集合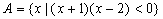 ,集合
,集合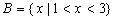 ,则
,则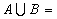
(A)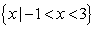 (B)
(B)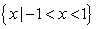 (C)
(C)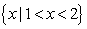 (D)
(D)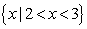
【答案】A
【解析】∵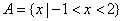 ,
,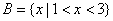 ,
, ,选A.
,选A.
2.设向量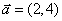 与向量
与向量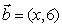 共线,则实数
共线,则实数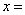
(A)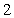 (B)
(B)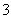 (C)
(C) 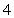 (D)
(D) 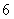
【答案】B
【解析】由共线向量 ,
,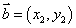 的坐标运算可知
的坐标运算可知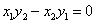 ,
,
即 ,选B.
,选B.
3.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是
(A)抽签法 (B)系统抽样法
(C)分层抽样法 (D)随机数法
【答案】C
【解析】因为是为了解各年级之间的学生视力是否存在显著差异,所以选择分层抽样法。
4.设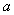 ,
,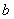 为正实数,则“
为正实数,则“ ”是“
”是“ ”的
”的
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D)既不充分也不必要条件
【答案】A
【解析】由已知当 时,
时,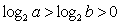 ∴,“
∴,“ ”是“
”是“ ”的充分条件。反过来由
”的充分条件。反过来由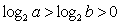 ,可得
,可得 ,∴“
,∴“ ”是“
”是“ ”的必要条件,综上,“
”的必要条件,综上,“ ”是“
”是“ ”的充要条件,选A.
”的充要条件,选A.
5.下列函数中,最小正周期为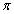 的奇函数是
的奇函数是
A.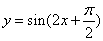 B.
B.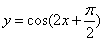
C.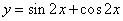 D.
D.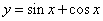
【答案】A
【解析】
A. 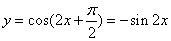 ,可知其满足题意;
,可知其满足题意;
B. 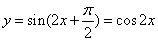 ,可知其最小正周期为
,可知其最小正周期为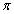 ,偶函数;
,偶函数;
C.  ,最小正周期为
,最小正周期为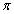 ,非奇非偶函数;
,非奇非偶函数;
 D.
D. 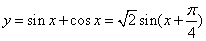 ,可知其最小正周期为
,可知其最小正周期为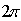 ,非奇非偶函数.选A
,非奇非偶函数.选A
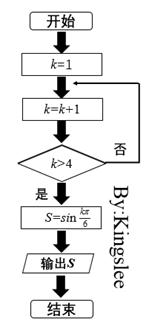
6.执行如图所示的程序框图,输出S的值是
(A) 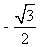 (B)
(B) 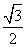 (C)-
(C)-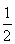 (D)
(D) 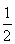
【答案】D
【解析】易得当k=1,2,3,4时执行的是否,当k=5时就执行是的步骤,
所以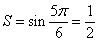 ,选D.
,选D.
7.过双曲线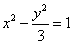 的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A,B两点,则
的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A,B两点,则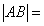
(A) (B)
(B)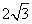 (C)6 (D)
(C)6 (D)
【答案】D
【解析】由题意可知双曲线的渐近线方程为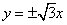 ,且右焦点
,且右焦点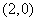 ,则直线
,则直线 与两条渐近线的交点分别为
与两条渐近线的交点分别为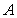
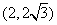 ,
,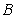
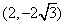 ,∴
,∴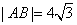 ,选D.
,选D.
8. 某食品的保鲜时间 (单位:小时)与储藏温度
(单位:小时)与储藏温度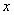 (单位:
(单位: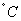 )满足函数关系
)满足函数关系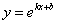 (
( 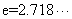 为自然对数的底数,k,b为常数)。若该食品在
为自然对数的底数,k,b为常数)。若该食品在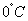 的保鲜时间是192小时,在23
的保鲜时间是192小时,在23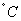 的保鲜时间是48小时,则该食品在33
的保鲜时间是48小时,则该食品在33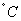 的保鲜时间是
的保鲜时间是
(A)16小时 (B)20小时 (C)24小时 (D)21小时
【答案】C
【解析】
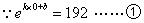 ,
,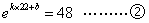 ,∴
,∴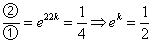 ,
,
∴当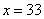 时,
时,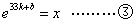 ,∴
,∴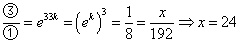 ,选C.
,选C.
9. 设实数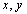 满足
满足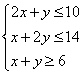 ,则
,则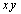 的最大值为
的最大值为
(A)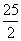 (B)
(B) 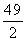 (C) 12 (D)14
(C) 12 (D)14
【答案】A
【解析】由第一个条件得: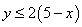 。于是,
。于是,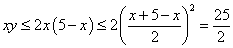 ,
,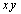 当且仅当
当且仅当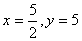 时取到最大值
时取到最大值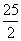 。经验证,
。经验证,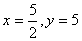 在可行域内,选
在可行域内,选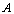 .
.
10.设直线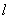 与抛物线
与抛物线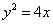 相交于A,B两点,与圆
相交于A,B两点,与圆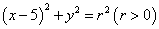 相切于点M,且M为线 段AB的中点.若这样的直线
相切于点M,且M为线 段AB的中点.若这样的直线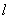 恰有4条,则
恰有4条,则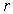 的取值范围是
的取值范围是
 (A)
(A)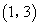 (B)
(B)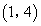 (C)
(C) (D)
(D)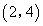
【答案】D
【解析】
设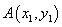 ,
,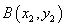 ,
,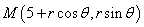 ,则
,则
两式相减,得: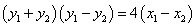 ,当直线
,当直线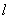 的斜率不存在时,显然符合条件的直线
的斜率不存在时,显然符合条件的直线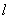 有两条。当直线
有两条。当直线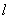 的斜率存在时,可得:
的斜率存在时,可得: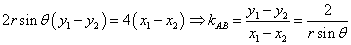 ,又∵
,又∵
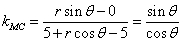 ,∴
,∴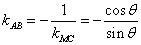 ,∴
,∴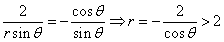
由于M在抛物线的内部,∴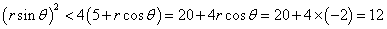 ,
,
∴ ,∴
,∴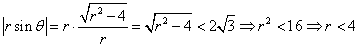 ,
,
因此,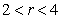 ,选D.
,选D.
第Ⅱ卷(非选择题共100分)
注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目说只是的区域内作答。作图可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚。答在试卷、草稿纸上无效。
二、填空题:本大题共5小题,每小题5分,共25分。
11. 设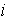 是虚数单位,则复数
是虚数单位,则复数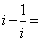 _________.
_________.
【答案】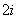
【解析】由题意可知: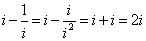
12. 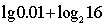 的值是 ________.
的值是 ________.
【答案】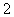
【解析】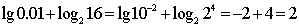
13. .已知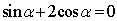 ,则
,则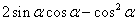 的值是________.
的值是________.
【答案】-1
【解析】由已知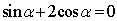 得,
得,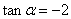 ,
,
∴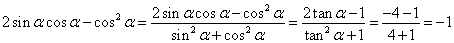
14. 三棱柱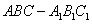 中,
中,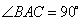 ,其正视图和侧视图都是边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,设点M,N,P分别是
,其正视图和侧视图都是边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,设点M,N,P分别是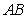 ,
,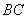 ,
,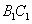 的中点,则三棱锥
的中点,则三棱锥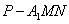 的体积是_______.
的体积是_______.
【答案】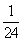
【解析】采用等积法,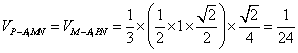
15.已知函数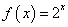 ,
, (其中
(其中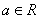 )。对于不相等的实数
)。对于不相等的实数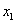 ,
,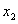 ,设
,设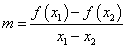 ,
,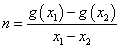 ,现有如下命题:
,现有如下命题:
(1) 对于任意不相等的实数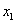 ,
,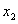 ,都有
,都有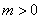 ;
;
(2) 对于任意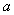 的及任意不相等的实数
的及任意不相等的实数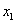 ,
,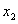 ,都有
,都有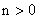 ;
;
(3) 对于任意的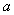 ,存在不相等的实数
,存在不相等的实数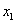 ,
,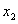 ,使得
,使得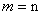 ;
;
(4) 对于任意的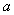 ,存在不相等的实数
,存在不相等的实数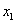 ,
,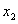 ,使得
,使得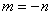 。
。
其中的真命题有_________________(写出所有真命题的序号)。
【答案】(1) (4)
【解析】
(1)设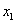 ,
,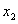 ,∵函数
,∵函数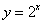 是增函数,∴
是增函数,∴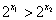 ,
,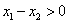 , 则
, 则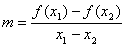 =
=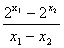 >0,所以正确;
>0,所以正确;
(2)设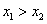 ,则
,则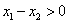 ,∴
,∴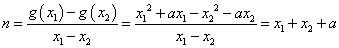
不妨我们设 ,则
,则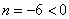 ,矛盾,所以(2)错。
,矛盾,所以(2)错。
(3)∵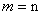 ,由(1)(2)可得:
,由(1)(2)可得: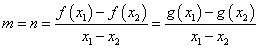 ,化简得到,
,化简得到,
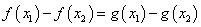 ,也即
,也即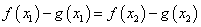 ,令
,令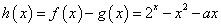 ,即对于任意的
,即对于任意的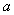 函数
函数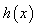 在定义域范围内存在有两个不相等的实数根
在定义域范围内存在有两个不相等的实数根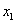 ,
,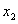 。则
。则
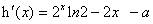 ,显然当
,显然当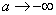 时,
时,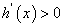 恒成立,即
恒成立,即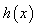 单调递增,最多与x轴有一个交点,不满足题意,所以错误。
单调递增,最多与x轴有一个交点,不满足题意,所以错误。
(4)同理可得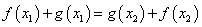 ,设
,设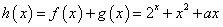 ,即对于任意的
,即对于任意的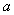 函数
函数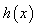 在定义域范围内存在有两个不相等的实数根
在定义域范围内存在有两个不相等的实数根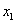 ,
,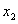 ,从而
,从而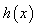 不是恒为单调函数。
不是恒为单调函数。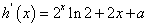 ,
,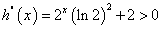 恒成立,∴
恒成立,∴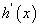 单调递增,又∵
单调递增,又∵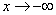 时,
时,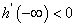 ,
,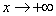 时,
时, 。所以
。所以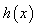 为先减后增的函数,满足要求,所以正确。
为先减后增的函数,满足要求,所以正确。
三、简答题:本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分12分)
设数列 的前
的前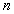 项和
项和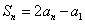 ,且
,且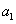 ,
,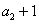 ,
,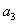 成等差数列。
成等差数列。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)记数列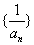 的前
的前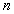 项和
项和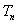 ,求
,求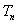 。
。
【解答】:
(Ⅰ)当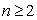 时有,
时有,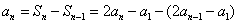
则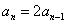
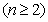 ,
,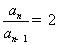 (
(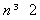 ) ,∴数列
) ,∴数列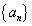 是以
是以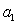 为首项,2为公比的等比数列。
为首项,2为公比的等比数列。
又由题意得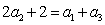 ,
,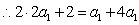 ,∴
,∴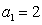 ,∴
,∴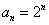
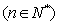
(Ⅱ)由题意得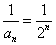 ,∴
,∴
17.(本小题满分12分)
一个小客车有5个座位,其座位号为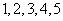 ,乘客
,乘客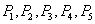 的座位号为
的座位号为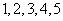 ,他们按照座位号顺序先后上车,乘客
,他们按照座位号顺序先后上车,乘客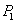 因身体原因没有坐自己号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位。如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
因身体原因没有坐自己号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位。如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(I)若乘客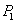 坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法。下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法。下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)

(II)若乘客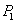 坐到了2号座位,其,他乘客按规则就坐,求乘客
坐到了2号座位,其,他乘客按规则就坐,求乘客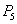 坐到5号座位的概率。
坐到5号座位的概率。
【解答】
(Ⅰ)当乘客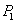 坐在3号位置上,此时
坐在3号位置上,此时 的位置没有被占,只能坐在2位置,
的位置没有被占,只能坐在2位置,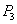 位置被占,可选剩下的任何,即可选1、4、5:①当
位置被占,可选剩下的任何,即可选1、4、5:①当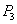 选1位置,
选1位置,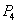 位置没被占,只能选4位置,
位置没被占,只能选4位置,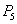 选剩下的,只有一种情况;②当
选剩下的,只有一种情况;②当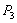 选4位置,
选4位置,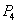 可选5位置也可选1位置,
可选5位置也可选1位置,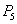 选剩下的,有两种情况;③当
选剩下的,有两种情况;③当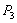 选5位置,
选5位置,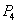 只可选4位置
只可选4位置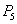 选剩下的,有一种情况;
选剩下的,有一种情况;

(Ⅱ)这个问情况比较复杂,需要列表解答,当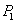 坐2位置时,
坐2位置时, 位置被占,可选剩下的
位置被占,可选剩下的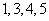 座位,下表列出了所有可能
座位,下表列出了所有可能
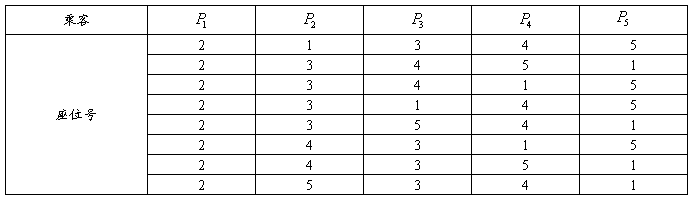
综上,共有8种情况,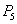 坐在5位置上的情况有4种,所求概率为
坐在5位置上的情况有4种,所求概率为
18.(本小题满分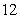 分)
分)
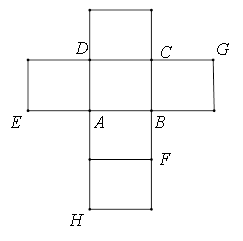
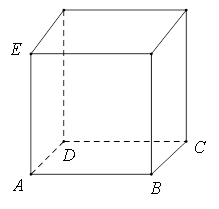
一个正方体的平面展开图及该正方体的直观图的示意图如图所示。
(I)请将字母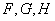 标记在正方体相应的顶点处(不需说明理由);
标记在正方体相应的顶点处(不需说明理由);
(II)判断平面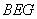 与平面
与平面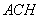 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(III)证明: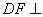 平面
平面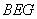
。
【解答】
(I)如答图1所示


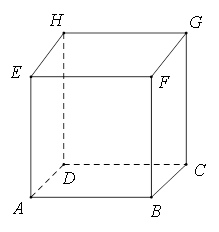
答图1 答图2 答图3
(II)如答图2所示,连接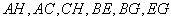 ,易得四边形
,易得四边形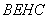 和四边形
和四边形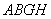 为
为 ,所以
,所以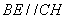 ,
,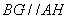 ,又∵
,又∵ 平面
平面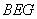 ,且
,且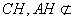 平面
平面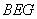 ,∴
,∴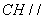 平面
平面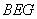 ,
,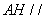 平面
平面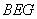 ,又∵
,又∵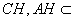 平面
平面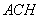 ,且
,且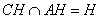 ,所以平面
,所以平面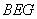
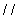 平面
平面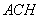
(III)如答图3所示,易得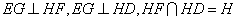 ,∴
,∴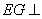 平面
平面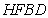 ,
,
得∵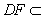 平面
平面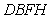 ,∴
,∴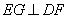 ,同理可得,
,同理可得,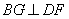 ,又
,又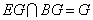 ,
,
∴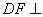 平面
平面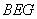 。
。
19.(本小题满分12分)
已知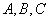 为
为 的内角,
的内角,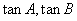 是关于
是关于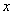 的方程
的方程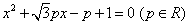 的两实根.
的两实根.
(Ⅰ)求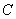 的大小;
的大小;
(Ⅱ)若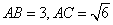 ,求
,求 的值.
的值.
【解答】
(Ⅰ)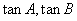 是关于
是关于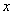 的方程
的方程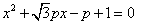 的两个根可得:
的两个根可得: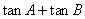
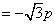 ,
,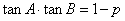 ,所以
,所以
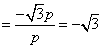 ,则
,则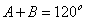 ,由三角形内角和为
,由三角形内角和为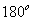 可知,
可知,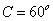 .
.
(Ⅱ)在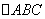 中,由正弦定理可得,
中,由正弦定理可得,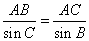 求得
求得 ,则
,则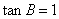 .又
.又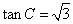 ,由三角形内角和为
,由三角形内角和为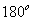 及诱导公式可知
及诱导公式可知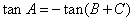 ,解得
,解得 ,将
,将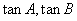 代入
代入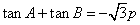 ,解得
,解得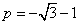 .
.
20.(本小题满分13分)
如图,椭圆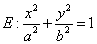 (
(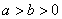 )的离心率是
)的离心率是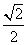 ,点
,点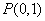 在短轴
在短轴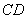 上,且
上,且 。
。
(Ⅰ)球椭圆 的方程;
的方程;
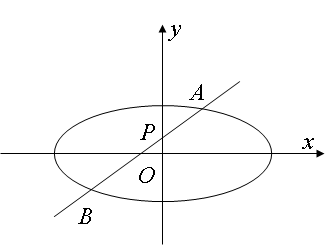 (Ⅱ)设
(Ⅱ)设 为坐标原点,过点
为坐标原点,过点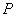 的动直线与椭圆交于
的动直线与椭圆交于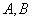 两点。是否存在常数
两点。是否存在常数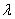 ,使得
,使得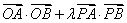 为定值?若存在,求
为定值?若存在,求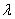 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
【解答】
(Ⅰ)由 知,
知,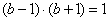 ,解得
,解得 ,
,
又∵由离心率是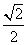 得到
得到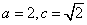 ;
;
∴椭圆E的方程为: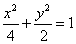 。
。
(Ⅱ)当直线AB的斜率存在时,设AB的解析式为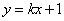 ,
,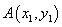 ,
,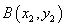
联立: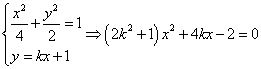 ,显然
,显然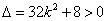 ,由韦达定理可知,
,由韦达定理可知,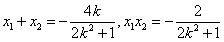 ,
,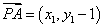 ,
,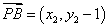
∴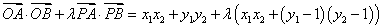 ,
,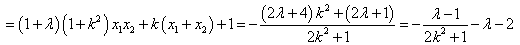
这里,与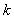 的取值无关,∴
的取值无关,∴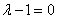 ,即
,即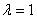 。
。
此时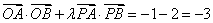 ,
,
当直线AB的斜率不存在时,AB就是CD,
那么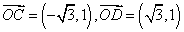
∴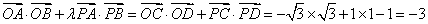
综上,存在常数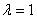 ,使得
,使得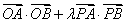 为定值
为定值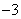 。
。
21.已知函数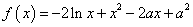 ,其中
,其中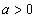 ,设
,设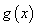 是
是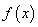 的导函数.
的导函数.
(Ⅰ)讨论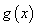 的单调性;
的单调性;
(Ⅱ)证明:存在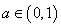 ,使得
,使得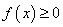 恒成立,且
恒成立,且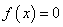 在区间(1,
在区间(1,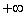 )内有唯一解。
)内有唯一解。
【解答】:
(Ⅰ)∵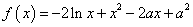 ,∴求导可得,
,∴求导可得,
 ,即
,即 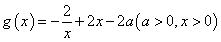
∴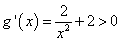 恒成立,∴
恒成立,∴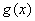 在其定义域上单调递增。
在其定义域上单调递增。
(Ⅱ)∵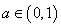 ,∴由(Ⅰ)可知
,∴由(Ⅰ)可知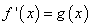 在(1,
在(1,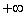 )内单调递增。
)内单调递增。
又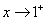 时,
时,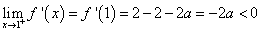 ,
,
当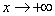 时,显然
时,显然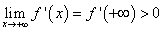 。而
。而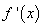 在(1,
在(1,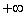 )是单调递增的,因此在
)是单调递增的,因此在
(1,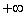 )内必定存在唯一的
)内必定存在唯一的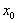 使得
使得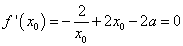 …………….. ①。
…………….. ①。
∴当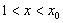 时,
时,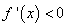 ,当
,当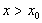 时,
时,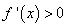
∴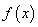 在
在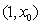 上单调递减,在
上单调递减,在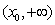 上单调递增,∴
上单调递增,∴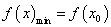 。
。
由已知条件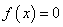 在区间
在区间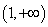 内有唯一解,∴必有
内有唯一解,∴必有 。
。
即 ……………………. ②,
……………………. ②,
由①式得到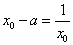 带入②式化简得:
带入②式化简得: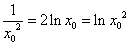 ,即
,即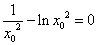 ,
,
令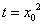 ,
,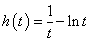 ,
,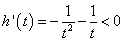 恒成立,∴
恒成立,∴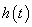 为减函数,
为减函数,
∵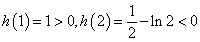 ,∴
,∴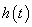 在
在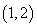 内有零点,即
内有零点,即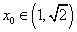 时,
时,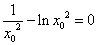 有解,此时
有解,此时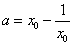 为增函数,且
为增函数,且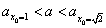 ,
,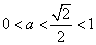
即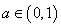 。∴存在
。∴存在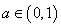 ,使得
,使得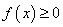 恒成立,且
恒成立,且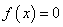 在区间(1,
在区间(1,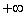 )内有唯一解。
)内有唯一解。
By:Kingslee QMJY 杰少
-
20xx四川高考作文浅析
20xx四川高考作文20xx3年6月7日20xx年全国高考今天正式拉开帷幕全国共有939万名考生走进考场随着首门语文科目考试的结束…
-
20xx高考满分作文——四川卷1
四川卷真题再现阅读下面的文字根据要求作文60分人只有在自己站起来之后这个世界才属于他这句话引发了你哪些思考请自选角度写一篇不少于8…
-
20xx四川高考语文卷 作文范文 人只有站起来 世界才属于他
改变自己四川省内江市翔龙中学高15级12班范思嘉生活中的人会遇到很多困难人只有自己站起来这个世界才属于他人只有强大自己才能强大社会…
-
20xx年四川高考作文
20xx年四川高考作文题目阅读下面的文字根据要求作文人只有在自己站起来之后这个世界才能属于他这句话引发了你哪些思考请自选角度写一篇…
-
20xx四川高考作文题及范文
20xx四川高考作文题阅读下面的文字根据要求作文人只有在自己站起来之后这个世界才能属于他这句话引发了你那些思考请自选角度写一篇不少…
-
初一期末班主任工作总结
班主任是学校教育工作的组织者,实施者,是教学工作的协调者,班级管理要求班主任热衷于本职工作,尽职尽则,锲而不舍,讲究方法。对学生的…
-
不定积分方法总结 2
不定积分方法总结一.一个重要思想拆分:用各种变换将一个合式分解成多个分式,这些分式的积分往往是好求的,再对每个分式进行积分,从而达…
-
靖口小学卫生室工作总结
卫生员薛江宏为了把学校卫生工作搞好,我认真学习《学校卫生工作条例》,做到热爱学校卫生事业、关爱学生,下面,我就今年的工作,作个简单…
-
20xx宿舍管理员工作总结
工作总结尊敬的公司领导:您们好!我叫陈林,来自贵州·铜仁。于20xx年x月x日起正式成为BYD汽车公司一员。能成为BYD汽车公司的…
-
七年级十三班文明礼貌月活动总结
我校三月份开展了“文明礼貌月”的活动。一个月以来,全校师生积极响应学校的号召,做文明人,说文明话,行文明事,使班风、学风有明显好转…