三角函数变换知识点总结
一、任意角和弧度制及任意的三角函数。
1.任意角
(1)角的分类
任意角按旋转方向可以分为正角、负角、零角。
(2)象限角
第一象限角的集合{x│k*360°<x<k*360°+90°,k∈Z}
第二象限角的集合{x│k*360°+90°<x<k*360°+180°,k∈Z}
第三象限角的集合{x│k*360°+180°<x<k*360°+270°,k∈Z}
第四象限角的集合{x│k*360°+270°<x<k*360°+360°,k∈Z}
终边在x轴上的角的集合{x│x=k*180°,k∈Z}
终边在x轴上的角的集合{x│x=k*180°+90°,k∈Z}
(3)角的度量
A、角的度量制有:角度制、弧度制
B、换算关系:1°=∏/180°rad,1rad=57.30°
2、任意角的三角函数
三角函数 正弦 余弦 正切
定 设a是一个任意角,它的终边与单位圆交于p(x、y),那么
义 y叫做a的正弦, x叫做a的余弦, y/x叫做a的正切 记作sina 记作cosx 记作tana
各 I + + +
象II + - -
限III - - +
符IV - + -
号 【口诀:一全正,二正弦,三正切,四余弦都为正值】
3.同角三角函数的基本关系
(1)平方关系:(sina)^2+(cosa)^2=1
(2)商数关系:sinx/cosx=tanx(x≠k∏+∏/2,k∈Z)
二、三角函数的诱导公式
1、下列各角的终边和角a的终边有何种关系
角 2k∏+a(k∈Z) ∏+a -a
与a角 sin( 2k∏+a)=a sin(∏+a)= -sina sin(-a)= -sina 终边的 cos( 2k∏+a)=a cos(∏+a)= -cosa cos(-a)=cosa 关系 tan( 2k∏+a)=a tan(∏+a)=tana tan(-a)= -tana 角 ∏-a ∏/2 -a ∏/2 +a
与a角 sin( ∏-a)=sina sin(∏/2-a)= cosa sin(-∏/2 +a)= cosa 终边的 cos( ∏-a)= -cosa cos(∏/2-a)= sina cos(-∏/2 +a)= -sina 关系 tan( ∏-a)= -tana
2、六组诱导公式
组数 一 二 三 四 五 六
角 2k∏+a(k∈Z) ∏+a -a ∏-a ∏/2-a ∏/2 +a 正弦 sina -sina -sina sina cosa cosa
余弦 cosa -cosa cosa -cosa sina -sina 正切 tana tana -tana -tana …… ……
口诀 【 函数名不变,符号看象限 】 【函数名改变,符号看象限】
三、三角函数的图像与性质
1、周期函数
(1)周期函数的定义
对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f(x+T)=f(x),那么函数f(x)就叫做周期函数(非零常数T叫做这个函数的周期)
如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期。
2.正弦函数、余弦函数、正切函数的性质
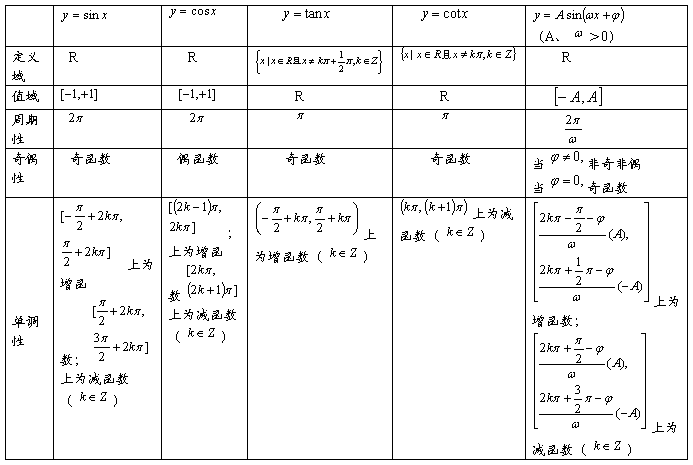
函数 y=sinx y=cosx y=tanx
定义域 x∈R x∈R x∈R且x≠∏/2+k∏,k∈Z 值域 [-1,1] [-1,1] R
单调性 在[-∏/2+2k∏, 在[-∏+2k∏, 2k∏] 在[-∏/2+k∏,∏/2+k∏] ∏/2+2k∏] 上递增k∈Z 上递增k∈Z
上递增,k∈Z
在[∏/2+2k∏, 在[2k∏, 2k∏+∏]
3∏/2+2k∏] 上递减k∈Z
上递减,k∈Z
最值 x=∏/2+2k∏时 x=2k∏时 无
ymax=1( k∈Z) ymax=1( k∈Z) 最
x=3∏/2+2k∏时 x=2k∏+∏时 值
ymax=-1( k∈Z) ymax=-1( k∈Z)
奇偶性 奇 偶 奇
对称中心 (k∏ ,0) (k∏+∏/2,0) (k∏/2,0)
对称轴 x=k∏+∏/2,k∈Z x=k∏,k∈Z ……
周期 2∏ 2∏ ∏
四、函数y=Axsin(ωx+ν)的图像及三角函数模型的简单应用
1相关概念
y=Axsin(ωx+v)(A>0,ω>0),x∈[0,+∞)表示一个振动量时
振幅:A
周期:T=2∏/ω
频率:f=1/T
相位:ωx+V
初相:V
2、用五点法画y=Axsin(ωx+v)一周期内的简图
利用五点法,如下表所示
x -V/ω (2∏-V)/ω (∏-V)/ω (3∏/2-V)/ω
ωx+V 0 ∏/2 ∏ 3∏/2
y=Axsin(ωx+v) 0 A 0 -A 0
五、两角和与差的正弦、余弦和正切公式
1、两角和与差的正弦、余弦和正切公式
C(a-B):cos(a-B)=cosacosB+sinasinB
C(a+B):cos(a+B)=cosacosB-sinasinB
S(a-B):sin(a-B)=sinacosB-cosasinB
S(a+B):sin(a+B)=sinacosB+cosasinB
T(a+B):tan(a+B)=(tana+tanB)/(1-tanatanB)
T(a-B):tan(a-B)=(tana-tanB)/(1+tanatanB)
2、二倍角的正弦、余弦、正切公式
S(2a):sin(2a)=2sinacosa
C(2a):cos(2a)=1-2(sina)^2=2(cosa)^2-1=(cosa)^2-(sina)^2
T(2a)=2tana/[1-(tana)^2]
3、公式的逆用及有关变形 (2∏-V)/ω2∏
tana±tanB=tan(a±+B)(1-(+)tanatanB)
sinacosa=1/2*sin2
1+sin2a=(sina+cosa)^2
1-sin2a=(sina-cosa)^2
sina+cosa=√2sin(a±∏/4)
(sina)^2=(1-cos2a)/2
(cosa)^2=(1+cos2a)/2
(tan)^2=(1-cosa)/(1+cosa)
4、角的变换
a=(a+B)-B
B=(a+B)-a
2a=(a+B)+(a-B)
2B=(a+B)-(a-B)
2两角和与差的三角函数:
cos(α+β)=cosα2cosβ-sinα2sinβ
cos(α-β)=cosα2cosβ+sinα2sinβ
sin(α±β)=sinα2cosβ±cosα2sinβ
tan(α+β)=(tanα+tanβ)/(1-tanα2tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα2tanβ)
2辅助角公式:
Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中
sint=B/(A^2+B^2)^(1/2)
cost=A/(A^2+B^2)^(1/2)
2倍角公式:
sin(2α)=2sinα2cosα=2/(tanα+cotα)
cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)
tan(2α)=2tanα/[1-tan^2(α)]
2三倍角公式:
sin(3α)=3sinα-4sin^3(α)
cos(3α)=4cos^3(α)-3cosα
2半角公式:
sin(α/2)=±√((1-cosα)/2)
cos(α/2)=±√((1+cosα)/2)
tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα
2降幂公式
sin^2(α)=(1-cos(2α))/2=versin(2α)/2
cos^2(α)=(1+cos(2α))/2=vercos(2α)/2
tan^2(α)=(1-cos(2α))/(1+cos(2α))
2万能公式:
sinα=2tan(α/2)/[1+tan^2(α/2)]
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]
tanα=2tan(α/2)/[1-tan^2(α/2)]
2积化和差公式:
sinα2cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα2sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα2cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα2sinβ=-(1/2)[cos(α+β)-cos(α-β)]
2和差化积公式:
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
2其他:
sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0 cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及
sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2
tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0
第二篇:三角函数知识点总结
三角函数
3、弧长公式: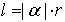 . 扇形面积公式:
. 扇形面积公式: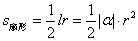
5、三角函数在各象限的符号:(一全二正弦,三切四余弦)
“一全正;二正弦;三两切;四余弦”。意思:第一象限内任何一个角的四种三角函数值都是“+”; 第二象限内只有正弦是“+”,其余全部是“-”; 第三象限内只有正切和余切是“+”,其余全部是“-”; 第四象限内只有余弦是“+”,其余全部是“-”。

7. 三角函数的定义域:
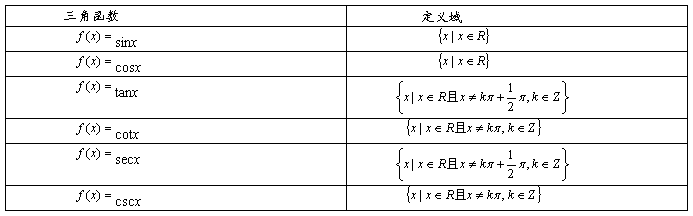
8、同角三角函数的基本关系式: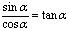
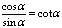
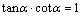
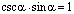
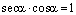
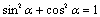
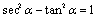
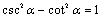
9、诱导公式:

“奇变偶不变,符号看象限” “奇、偶”指的是π/2的倍数的奇偶,“变与不变”指的是三角函数的名称的变化:“变”是指正弦变余弦,正切变余切。(反之亦然成立)“符号看象限”的含义是:把角α看做锐角,不考虑α角所在象限,看n·(π/2)±α是第几象限角,从而得到等式右边是正号还是负号。
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sec(π/2+α)=-cscα
csc(π/2+α)=secα
三角函数的公式:(一)基本关系
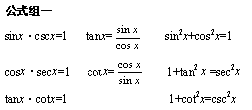
(二)角与角之间的互换
公式组一 公式组二


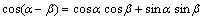
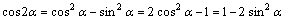

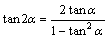
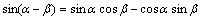
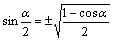
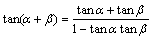
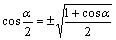
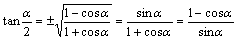
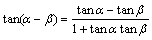
公式组三 公式组四



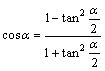
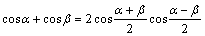
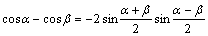

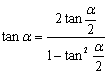
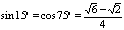 ,,
,,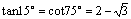 ,.
,. 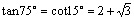
10. 正弦、余弦、正切、余切函数的图象的性质:
 注意:①
注意:① 与
与 的单调性正好相反;
的单调性正好相反;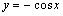 与
与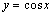 的单调性也同样相反.一般地,若
的单调性也同样相反.一般地,若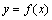 在
在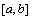 上递增(减),则
上递增(减),则 在
在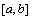 上递减(增).
上递减(增).
②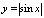 与
与 的周期是
的周期是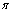 .
.
③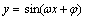 或
或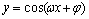 (
(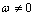 )的周期
)的周期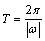 .
.
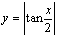 的周期为2
的周期为2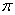 (
(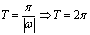 ,如图,翻折无效).
,如图,翻折无效).
⑤当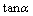 ·
·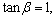
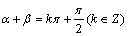 ;
;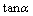 ·
·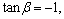
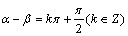 .
.
⑥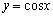 与
与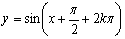 是同一函数,而
是同一函数,而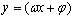 是偶函数,则
是偶函数,则
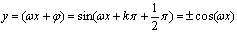 .
.
⑦函数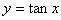 在
在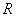 上为增函数.(×) [只能在某个单调区间单调递增. 若在整个定义域,
上为增函数.(×) [只能在某个单调区间单调递增. 若在整个定义域,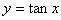 为增函数,同样也是错误的].
为增函数,同样也是错误的].
⑧定义域关于原点对称是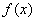 具有奇偶性的必要不充分条件.(奇偶性的两个条件:一是定义域关于原点对称(奇偶都要),二是满足奇偶性条件,偶函数:
具有奇偶性的必要不充分条件.(奇偶性的两个条件:一是定义域关于原点对称(奇偶都要),二是满足奇偶性条件,偶函数: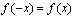 ,奇函数:
,奇函数: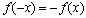 )
)
奇偶性的单调性:奇同偶反. 例如: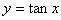 是奇函数,
是奇函数,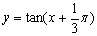 是非奇非偶.(定义域不关于原点对称)
是非奇非偶.(定义域不关于原点对称)
奇函数特有性质:若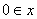 的定义域,则
的定义域,则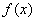 一定有
一定有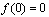 .(
.(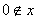 的定义域,则无此性质)
的定义域,则无此性质)
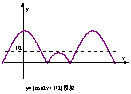
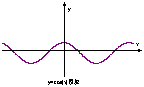 ⑨
⑨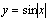 不是周期函数;
不是周期函数;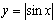 为周期函数(
为周期函数(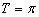 );
);
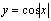 是周期函数(如图);
是周期函数(如图); 为周期函数(
为周期函数(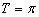 );
);
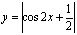 的周期为
的周期为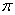 (如图),并非所有周期函数都有最小正周期,例如:
(如图),并非所有周期函数都有最小正周期,例如:
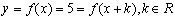 .
.
⑩ 有
有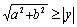 .
.
三角函数的图象变换有振幅变换、周期变换和相位变换等.
函数y=Asin(ωx+φ)的振幅|A|,周期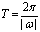 ,频率
,频率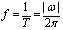 ,相位
,相位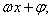 初相
初相 (即当x=0时的相位).(当A>0,ω>0 时以上公式可去绝对值符号),
(即当x=0时的相位).(当A>0,ω>0 时以上公式可去绝对值符号),
由y=sinx的图象上的点的横坐标保持不变,纵坐标伸长(当|A|>1)或缩短(当0<|A|<1)到原来的|A|倍,得到y=Asinx的图象,叫做振幅变换或叫沿y轴的伸缩变换.(用y/A替换y)
由y=sinx的图象上的点的纵坐标保持不变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到原来的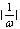 倍,得到y=sinω x的图象,叫做周期变换或叫做沿x轴的伸缩变换.(用ωx替换x)
倍,得到y=sinω x的图象,叫做周期变换或叫做沿x轴的伸缩变换.(用ωx替换x)
由y=sinx的图象上所有的点向左(当φ>0)或向右(当φ<0)平行移动|φ|个单位,得到y=sin(x+φ)的图象,叫做相位变换或叫做沿x轴方向的平移.(用x+φ替换x)
由y=sinx的图象上所有的点向上(当b>0)或向下(当b<0)平行移动|b|个单位,得到y=sinx+b的图象叫做沿y轴方向的平移.(用y+(-b)替换y)
由y=sinx的图象利用图象变换作函数y=Asin(ωx+φ)(A>0,ω>0)(x∈R)的图象,要特别注意:当周期变换和相位变换的先后顺序不同时,原图象延x轴量伸缩量的区别。
4、反三角函数:
函数y=sinx,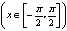 的反函数叫做反正弦函数,记作y=arcsinx,它的定义域是[-1,1],值域是
的反函数叫做反正弦函数,记作y=arcsinx,它的定义域是[-1,1],值域是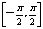 .
.
函数y=cosx,(x∈[0,π])的反应函数叫做反余弦函数,记作y=arccosx,它的定义域是[-1,1],值域是[0,π].
函数y=tanx,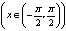 的反函数叫做反正切函数,记作y=arctanx,它的定义域是(-∞,+∞),值域是
的反函数叫做反正切函数,记作y=arctanx,它的定义域是(-∞,+∞),值域是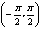 .
.
函数y=ctgx,[x∈(0,π)]的反函数叫做反余切函数,记作y=arcctgx,它的定义域是(-∞,+∞),值域是(0,π).
一、反三角函数.
1. 反三角函数:⑴反正弦函数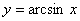 是奇函数,故
是奇函数,故 ,
,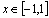 (一定要注明定义域,若
(一定要注明定义域,若 ,没有
,没有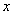 与
与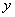 一一对应,故
一一对应,故 无反函数)
无反函数)
注: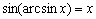 ,
,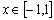 ,
,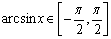 .
.
⑵反余弦函数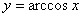 非奇非偶,但有
非奇非偶,但有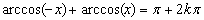 ,
,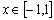 .
.
注:①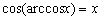 ,
,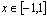 ,
,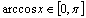 .
.
②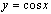 是偶函数,
是偶函数,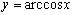 非奇非偶,而
非奇非偶,而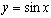 和
和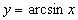 为奇函数.
为奇函数.
⑶反正切函数: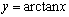 ,定义域
,定义域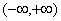 ,值域(
,值域(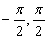 ),
), 是奇函数,
是奇函数,
 ,
,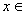
 .
.
注: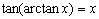 ,
,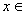
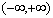 .
.
⑷反余切函数: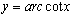 ,定义域
,定义域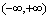 ,值域(
,值域(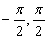 ),
),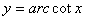 是非奇非偶.
是非奇非偶.
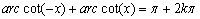 ,
,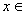
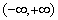 .
.
注:①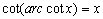 ,
,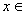
 .
.
②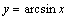 与
与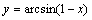 互为奇函数,
互为奇函数,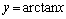 同理为奇而
同理为奇而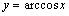 与
与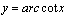 非奇非偶但满足
非奇非偶但满足 .
.
-
函授毕业生自我鉴定范文
函授毕业生自我鉴定范文为了提高自己的业务水平和能力,我参加了20xx年的成人高考,考取了曲阜师范大学的汉语言文学专业,于是开始了三…
-
大学生在校实习证明函
大学生在校实习证明我单位____同志,累计从事工程咨询相关专业工作共____年。起止年月从事何种专业工作专业技术职务年月-年月年月…
-
初中数学函数知识总结归纳
初中数学函数知识总结归纳1.常量和变量在某变化过程中可以取不同数值的量,叫做变量.在某变化过程中保持同一数值的量或数,叫常量.2.…
-
函授本科自我鉴定
函授本科自我鉴定虽然在职,但是我不满足于自己的知识,更为了提高自己的业务水平和能力,我利用业余时间参加了函授,希望不断地学习和完善…
-
数学分析下——平面点集与多元函数知识点
数学分析下定义定理整理第一章多元函数的极限与连续第一节平面点集与多元函数1、坐标平面上满足某种条件P的点的集合称为平面点集,并记作…
-
公函格式范文
1.概述函,即信函,或称书信。公函,即处理公务所用的书信。公函是党政机关、人民团体、企事业单位间商洽和联系工作时使用的一种文体。公…
-
公文函格式范文
公文函格式范文公文函概念函,即信;公函即公务信件。它是高低级和平行机关或不相附属机关之间在商洽和接洽工作、询问和答复问题时所应用的…
-
回复函格式及范文
回复函格式及范文1、概述答复即复函,属公函的一种。复函是机关、单位为答复来函一方面商洽、询问或联系事宜而使用的一种公文,既可用于上…
-
函的用途、类别、格式、写法及范文解析
函的用途、类别、格式、写法及范文解析(一)含义、功用和性质“函”,是“适用于不相隶属机关之间商洽工作、询问和答复问题,请求批准和答…
-
投标邀请函范文
篇一:投标邀请书范文致:________________________1、___________________________…