三角函数画图方法总结
y=Asin(ωx+φ)+k(A>0,ω>0)
先相位变换,再周期变换
(1)x轴方向平移变换(相位变换):y=sin(x)图象上所有点, 在x轴方向平移|φ|个单位(φ>0向左,φ<0向右), 得到y=sin(x+j)图象
(2)x轴方向伸缩变换(周期变换):y=sin(x+φ)图象上所有点的横坐标 伸缩到原来的1/ω倍(纵坐标不变)(ω>1缩短,0<ω<1伸长),得到y=sin(ωx+φ)图象
(3)y轴方向伸缩变换(振幅变换):y=sin(ωx+φ) 图象上所有点的纵坐标 伸缩到原来的A倍(横坐标不变)(A>1伸长,0<A<1缩短),得到y=Asin(ωx+φ )图象
(4)y轴方向平移变换 :y= Asin(ωx+φ)图象上所有点, 在y轴方向平移k个单位(k>0向上,k<0向下), 得到y=Asin(ωx+φ)+k图象
先周期变换,再相位变换
(1)x轴方向伸缩变换(周期变换):y=sin(x)图象上所有点的横坐标,伸缩到原来的1/ω倍(纵坐标不变)(ω>1缩短,0<ω<1伸长),得到y=sin(ωx)图象
(2)x轴方向平移变换(相位变换):y=sin(ωx )图象上所有点, 在x轴方向平移|j|ω个单位(φ>0向左,φ<0向右),得到y=sin(ωx+φ)图象
(3)y轴方向伸缩变换(振幅变换):y=sin(ωx+φ) 图象上所有点的纵坐标 伸缩到原来的A倍(横坐标不变)(A>1伸长,0<A<1缩短),得到y=Asin(ωx+φ )图象
(4)y轴方向平移变换 :y= Asin(ωx+φ)图象上所有点, 在y轴方向平移k个单位(k>0向上,k<0向下), 得到y=Asin(ωx+φ)+k图象
第二篇:三角函数思想方法总结
三角函数思想方法总结
一、八卦图
例题:若α是第三象限的角,问α/2是哪个象限的角?2α是哪个象限的角?
 各个象限的半角范围可以用下图记忆,图中的Ⅰ、Ⅱ、Ⅲ、Ⅳ分别指第一、二、三、四象限角的半角范围;
各个象限的半角范围可以用下图记忆,图中的Ⅰ、Ⅱ、Ⅲ、Ⅳ分别指第一、二、三、四象限角的半角范围;
口诀:“两等分各象限、一二三四”确定
二:三角函数线
设角α的顶点在坐标原点,始边与x轴正半轴重合,终边与单位圆相交于点P,过P作PM垂直于x轴于M,则点M是点P在x轴上的__________.由三角函数的定义知,点P的坐标为________________,即______________,其中cos α=______,sin α=______,单位圆与x轴的正半轴交于点A,单位圆在A点的切线与α的终边或其反向延长线相交于点T,则tan α=______.我们把有向线段OM、MP、AT叫做α的__________、__________、__________.

三角函数线是三角函数的几何表示
(1)正弦线、正切线的方向同纵轴一致,向上为正,向下为负.
(2)余弦线的方向同横轴一致,向右为正,向左为负.
(3)当角α的终边在x轴上时,点T与点A重合,此时正切线变成了一个点,
当角α的终边在y轴上时,点T不存在,即正切线不存在.
(4)在“数”的角度认识任意角的三角函数的基础上,还可以从图形角度考察
任意角的三角函数,即用有向线段表示三角函数值,这是三角函数与其他
基本初等函数不同的地方.
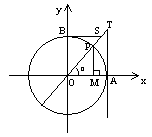 三角函数线的特征是:正弦线MP“站在
三角函数线的特征是:正弦线MP“站在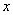 轴上(起点在
轴上(起点在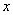 轴上)”、余弦线OM“躺在
轴上)”、余弦线OM“躺在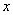 轴上(起点是原点)”、正切线AT“站在点
轴上(起点是原点)”、正切线AT“站在点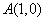 处(起点是
处(起点是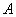 )”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。如
)”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。如
(1)若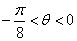 ,则
,则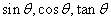 的大小关系为_____
的大小关系为_____
(答: );
);
(2)若 为锐角,则
为锐角,则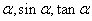 的大小关系为_______
的大小关系为_______
(答: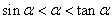 );
);
(3)函数 的定义域是_______
的定义域是_______
(答: )
)
例3:(1)求函数y=lg(3-4sin2x)的定义域;
(2)设θ是第二象限角,试比较sin ,cos ,tan 的大小.
审题视角 (1)求定义域,就是求使3-4sin2x>0的x的范围.用三角函数线求解.
(2)比较大小,可以从以下几个角度观察:
①θ是第二象限角,是第几象限角?首先应予以确定.②sin ,cos ,tan 不能求出确定值,但可以画出三角函数线.③借助三角函数线比较大小.
规范解答
 解 (1)∵3-4sin2x>0,∴sin2x<,
解 (1)∵3-4sin2x>0,∴sin2x<,
∴-<sin x<.
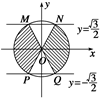
利用三角函数线画出x满足条件的终边范围(如图阴影部分所示),
∴x∈(k∈Z).
(2)∵θ是第二象限角,
 ∴+2kπ<θ<π+2kπ,k∈Z,
∴+2kπ<θ<π+2kπ,k∈Z,
∴+kπ<<+kπ,k∈Z,
∴是第一或第三象限的角.
(如图阴影部分),结合单位圆上的三角函数线可得:
①当是第一象限角时,
sin =AB,cos =OA,tan =CT,
从而得,cos <sin <tan ;
②当是第三象限角时,
sin =EF,cos =OE,tan =CT,
得sin <cos <tan .
综上所得,当在第一象限时,cos <sin <tan ;
当在第三象限时,sin <cos <tan .
批阅笔记 (1)第(1)小题的实质是解一个简单的三角不等式,可以用三角函数图像,也可以用三角函数线,用三角函数线更方便.(2)第(2)小题比较大小,由于没有给出具体的角度,所以用图形可以更直观的表示.(3)本题易错点:①不能确定所在的象限;②想不到应用三角函数线.原因在于概念理解不透,方法不够灵活.
方法与技巧
1.在利用三角函数定义时,点P可取终边上任一点,如有可能则取终边与单位圆的交点.|OP|=r一定是正值.
2.三角函数符号是重点,也是难点,在理解的基础上可借助口诀:sin α上正下负;
cos α右正左负;tan α奇正偶负.
3.在解简单的三角不等式时,利用单位圆及三角函数线是一个小技巧.
三、三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构。即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心!第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点。
基本的技巧有:
(1)巧变角(已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换. 如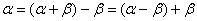 ,
, ,
,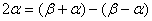 ,
, ,
,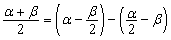 等),如
等),如
(1)已知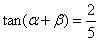 ,
,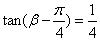 ,那么
,那么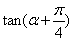 的值是_____
的值是_____
(答: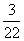 );
);
(2)已知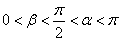 ,且
,且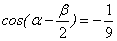 ,
,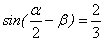 ,求
,求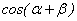 的值
的值
(答: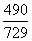 );
);
(3)已知 为锐角,
为锐角,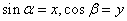 ,
,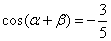 ,则
,则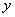 与
与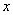 的函数关系为______
的函数关系为______
(答: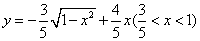 )
)
(2)三角函数名互化(切割化弦),如
(1)求值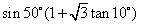
(答:1);
(2)已知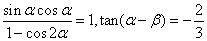 ,求
,求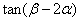 的值
的值
(答: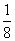 )
)
(3)公式变形使用(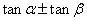
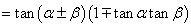 。如
。如
(1)已知A、B为锐角,且满足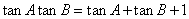 ,则
,则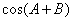 =_____
=_____
(答: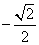 );
);
(2)设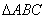 中,
中,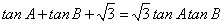 ,
,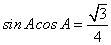 ,则此三角形是____三角形
,则此三角形是____三角形
(答:等边)
(4)三角函数次数的降升(降幂公式: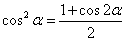 ,
,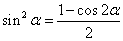 与升幂公式:
与升幂公式: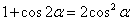 ,
,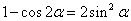 )。如
)。如
(1)若 ,化简
,化简 为_____
为_____
(答: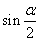 );
);
(2)函数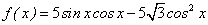
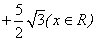 的单调递增区间为____
的单调递增区间为____
(答: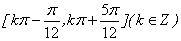 )
)
(5)式子结构的转化(对角、函数名、式子结构化同)。如
(1)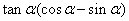

(答: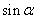 );
);
(2)求证: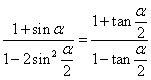 ;
;
(3)化简: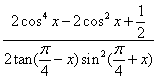
(答: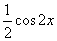 )
)
(6)常值变换主要指“1”的变换(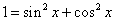
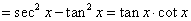
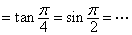 等),如已知
等),如已知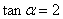 ,求
,求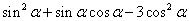 (答:
(答: ).
).
(7)正余弦“三兄妹—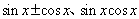 ”的内存联系——“知一求二”,如
”的内存联系——“知一求二”,如
(1)若  ,则
,则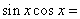 __
__
(答: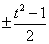 ),特别提醒:这里
),特别提醒:这里 ;
;
(2)若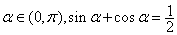 ,求
,求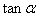 的值。
的值。
(答: );
);
(3)已知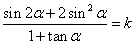
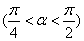 ,试用
,试用 表示
表示 的值
的值
(答: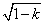 )。
)。
13、辅助角公式中辅助角的确定: (其中
(其中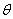 角所在的象限由a, b的符号确定,
角所在的象限由a, b的符号确定,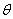 角的值由
角的值由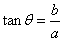 确定)在求最值、化简时起着重要作用。如
确定)在求最值、化简时起着重要作用。如
(1)若方程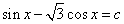 有实数解,则
有实数解,则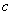 的取值范围是___________.
的取值范围是___________.
(答:[-2,2]);
(2)当函数 取得最大值时,
取得最大值时, 的值是______
的值是______
(答: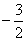 );
);
(3)如果 是奇函数,则
是奇函数,则 =
=
(答:-2);
(4)求值: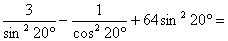 ________
________
(答:32)
-
高一数学必修四三角函数总结
高一数学必修四三角函数总结同角三角函数的基本关系倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1商的关…
-
高中三角函数总结
三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cosAsinBco…
-
三角函数总结大全
三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。而掌握三角函数的内部规律及…
-
三角函数总结
三角函数巩固总结习题1.已知角a终边过点P(m,5),且cosa=m/13(m≠0),求m的值2.求函数f(x)=sin(x/2-…
-
三角函数总结大全(整理好的)
三角函数一任意角的三角函数及诱导公式1任意角的概念角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形一条射线由原…
-
三角函数题型分类总结
一.求值1.(09北京文)若sin???,tan??0,则cos??2.?是第三象限角,sin(???)?4515?,则cos??…
-
必修四三角函数的图象与性质总结
20xx年普通高考数学科一轮复习精品学案第23讲三角函数的图象与性质1正弦函数余弦函数正切函数的图像2三角函数的单调区间ysinx…
-
三角函数图像与性质知识点总结和经典题型
三角函数图像与性质知识点总结和经典题型1正弦函数余弦函数正切函数的图像2三角函数的单调区间2kkZ递减区间是ysinx的递增区间是…
-
三角函数知识点总结
高中数学第四章三角函数考试内容角的概念的推广弧度制任意角的三角函数单位圆中的三角函数线同角三角函数的基本关系式正弦余弦的诱导公式两…
-
必修四三角函数的图象与性质总结
20xx年普通高考数学科一轮复习精品学案第23讲三角函数的图象与性质1正弦函数余弦函数正切函数的图像2三角函数的单调区间ysinx…
-
公函格式范文
1.概述函,即信函,或称书信。公函,即处理公务所用的书信。公函是党政机关、人民团体、企事业单位间商洽和联系工作时使用的一种文体。公…