不等式知识点总结
不等关系与不等式
一.知识点总结:
1.不等关系与不等式
比差法:a>b a-b>0, a<b
a-b>0, a<b a-b<0,a=b
a-b<0,a=b a-b=0.问题的关键是判定差的符号(正,负,零),方法通常是配方或因式分解.
a-b=0.问题的关键是判定差的符号(正,负,零),方法通常是配方或因式分解.
2.不等式的性质
基本性质有: 运算性质有:
(1)a>bÛb<a (对称性) 1)a>b,c>dÞa+c>b+d. 5)a>b>0Þan>bn
(2)a>b,b>cÞa>c (传递性) 2) a>b,c<dÞa-c>b-d . 6)a>b>0Þ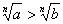 (nÎN,n>1)
(nÎN,n>1)
(3)a>bÛa+c>b+c 3) a>b>0,c>d>0Þac>bd.
(4)c>0时,a>bÛac>bc 4)a>b>0,0<c<dÞ
c<0时,a>bÛac<bc 5)a>b>0Þan>bn
6)a>b>0Þ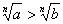
3.均值不等式
a,b∈R+, (当且仅当a=b时成立等号)
(当且仅当a=b时成立等号)
教材讲了利用它证明不等式和求最值,突出了求最值.可以把此不等式扩充为 (当且仅当a=b时成立等号).注意“凑”成可用定理的形式.
(当且仅当a=b时成立等号).注意“凑”成可用定理的形式.
例题
1).已知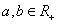 ,则下列各数
,则下列各数 从小到大的顺序是 .
从小到大的顺序是 .
2.)已知两正数x,y 满足x+y=1,则z= 的最小值为 .
的最小值为 .
3).已知a,b∈R,且满足a+3b=1,则ab的最大值为___________.
4.一元二次不等式
1)可以把“三个二次”结合起来,突出二次函数的作用.

对于二次项系数为负的情况可以类似研究,如果只是解不等式,可以首先把二次项系数调整为正.
2)解一元二次不等式 的思维过程:
的思维过程:
第一步,
第二步,
第三步,
3)含参问题,要会分类讨论。.
4)高次不等式:对可以分解为几个一次式之积形式的高次不等式应该会用穿线法解答,毕竟教材中有所体现(P.100B 3).
5)一元二次方程根的分布问题也是教材渗透出来的应该会处理的问题.(P80 B 3)
这类问题最好利用二次函数的图像研究:当两根位于不同区间时,只需研究区间端点处函数值的符号,无需研究对称轴及判别式;当两根位于同一区间时,不但要研究区间端点处函数值的符号,还需研究对称轴及判别式.
6)简单分式不等式、简单的指对不等式(P99 A 3,6;P103 4 )
5.恒成立问题
1)常用以下结论:k ≥ f(x)恒成立? k ≥ f(x)max, ;k ≤ f(x)恒成立? k ≤ f(x)min .(P.103 3)
2)注意它和存在性问题的区别:
存在x使k ≥ f(x)成立? k ≥ f(x)min ;存在x使k ≤ f(x)成立? k ≤ f(x)max .
6.实际应用
把实际问题通过建立不等式模型解决,教材中非常重视应用.
二.参考例题:
1.不等式ax + bx + c>0 的解集为(-
+ bx + c>0 的解集为(- ,2),对于系数a、b、c,有如下结论:
,2),对于系数a、b、c,有如下结论:
①a>0 ②b>0 ③ c>0 ④a + b + c>0 ⑤a – b + c>0,其中正确的结论的序号是_____________.
2.已知两个正变量x,y满足x+y=4,使不等式 恒成立的实数m的取值范围是 .
恒成立的实数m的取值范围是 .
3.不等式(x-2)2 (3-x) (x-4)3 (x-1)≥0的解集为 .
4.方程x2+(k-2)x+5-k=0的两根都大于2,求实数k的取值范围.
5.解关于x的不等式:ax2-(a+1)x+1<0
6.解关于x的不等式: .
.
7.若不等式 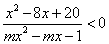 对一切x恒成立,求实数m的范围.(P80 A 6;P99 4)
对一切x恒成立,求实数m的范围.(P80 A 6;P99 4)
8.设不等式ax2+bx+c>0的解集是{x|α<x<β}(0<α<β),求不等式cx2+bx+a<0的解集.(P100B 6)
9.已知关于x的二次方程x2+2mx+2m+1=0
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的范围;
(2)若方程两根均在区间(0,1)内,求m的范围.
第二篇:不等式知识点总结
不等关系与不等式
一.知识点总结:
1.不等关系与不等式
比差法:a>b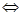 a-b>0, a<b
a-b>0, a<b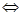 a-b<0,a=b
a-b<0,a=b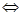 a-b=0.问题的关键是判定差的符号(正,负,零),方法通常是配方或因式分解.
a-b=0.问题的关键是判定差的符号(正,负,零),方法通常是配方或因式分解.
2.不等式的性质
基本性质有: 运算性质有:
(1)a>bÛb<a (对称性) 1)a>b,c>dÞa+c>b+d. 5)a>b>0Þan>bn
(2)a>b,b>cÞa>c (传递性) 2) a>b,c<dÞa-c>b-d . 6)a>b>0Þ (nÎN,n>1)
(nÎN,n>1)
(3)a>bÛa+c>b+c 3) a>b>0,c>d>0Þac>bd.
(4)c>0时,a>bÛac>bc 4)a>b>0,0<c<dÞ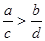
c<0时,a>bÛac<bc 5)a>b>0Þan>bn
6)a>b>0Þ
3.均值不等式
a,b∈R+,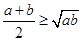 (当且仅当a=b时成立等号)
(当且仅当a=b时成立等号)
教材讲了利用它证明不等式和求最值,突出了求最值.可以把此不等式扩充为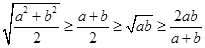 (当且仅当a=b时成立等号).注意“凑”成可用定理的形式.
(当且仅当a=b时成立等号).注意“凑”成可用定理的形式.
例题
1).已知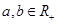 ,则下列各数
,则下列各数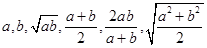 从小到大的顺序是 .
从小到大的顺序是 .
2.)已知两正数x,y 满足x+y=1,则z=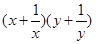 的最小值为 .
的最小值为 .
3).已知a,b∈R,且满足a+3b=1,则ab的最大值为___________.
4.一元二次不等式
1)可以把“三个二次”结合起来,突出二次函数的作用.

对于二次项系数为负的情况可以类似研究,如果只是解不等式,可以首先把二次项系数调整为正.
2)解一元二次不等式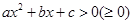 的思维过程:
的思维过程:
第一步,
第二步,
第三步,
3)含参问题,要会分类讨论。.
4)高次不等式:对可以分解为几个一次式之积形式的高次不等式应该会用穿线法解答,毕竟教材中有所体现.
5)简单分式不等式、简单的指对不等式(P99 A 3,6;P103 4 )
5.恒成立问题
1)常用以下结论:k ≥ f(x)恒成立? k ≥ f(x)max, ;k ≤ f(x)恒成立? k ≤ f(x)min .(P.103 3)
2)注意它和存在性问题的区别:
存在x使k ≥ f(x)成立? k ≥ f(x)min ;存在x使k ≤ f(x)成立? k ≤ f(x)max .
二.参考例题:
1.不等式ax + bx + c>0 的解集为(-
+ bx + c>0 的解集为(-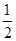 ,2),对于系数a、b、c,有如下结论:
,2),对于系数a、b、c,有如下结论:
①a>0 ②b>0 ③ c>0 ④a + b + c>0 ⑤a – b + c>0,其中正确的结论的序号是_____________.
2.已知两个正变量x,y满足x+y=4,使不等式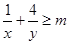 恒成立的实数m的取值范围是 .
恒成立的实数m的取值范围是 .
3.不等式(x-2)2 (3-x) (x-4)3 (x-1)≥0的解集为 .
4.方程x2+(k-2)x+5-k=0的两根都大于2,求实数k的取值范围.
5.解关于x的不等式:ax2-(a+1)x+1<0
6.解关于x的不等式: .
.
7.若不等式 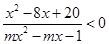 对一切x恒成立,求实数m的范围.(P80 A 6;P99 4)
对一切x恒成立,求实数m的范围.(P80 A 6;P99 4)
8.设不等式ax2+bx+c>0的解集是{x|α<x<β}(0<α<β),求不等式cx2+bx+a<0的解集.
9.已知关于x的二次方程x2+2mx+2m+1=0
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的范围;(2)若方程两根均在区间(0,1)内,求m的范围.
课后练习
1.解下列不等式:
(1)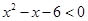 ;(2)
;(2)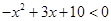 ;(3)
;(3)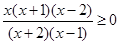 .
.
2.已知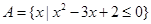 ,
,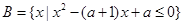 ,
,
(1)若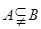 ,求
,求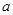 的取值范围;
的取值范围;
(2)若 ,求
,求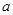 的取值范围.
的取值范围.
3.已知 ,
,
(1)如果对一切 ,
,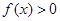 恒成立,求实数
恒成立,求实数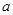 的取值范围;
的取值范围;
(2)如果对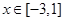 ,
,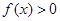 恒成立,求实数
恒成立,求实数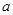 的取值范围
的取值范围
4.已知不等式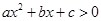 的解集为
的解集为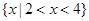 ,则不等式
,则不等式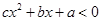 的解集为 .
的解集为 .
5.若不等式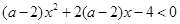 对一切
对一切 成立,则
成立,则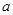 的取值范围.
的取值范围.
6.若关于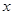 的方程
的方程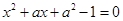 有一正根和一负根,则
有一正根和一负根,则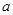 的取值范围.
的取值范围.
7.关于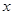 的方程
的方程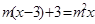 的解为不大于2的实数,则
的解为不大于2的实数,则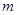 的取值范围.
的取值范围.
8.不等式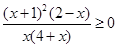 的解集为.
的解集为.
1.若x>0,求f(x)=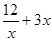 的最小值
的最小值
2.若x>0,求f(x)=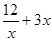 的最大值
的最大值
3.已知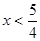 ,求函数
,求函数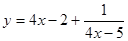 的最大值
的最大值
4.a,b∈R,且a+b=3,则2a+2b的最小值为 ( )
A.8 B.6
C.4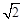 D.2
D.2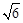
5.x>0,y>0,3x+y=12,则xy的最大值是__________, 的最小值是____________.
的最小值是____________.
6.函数y= 的最小值为_______________
的最小值为_______________
训练题
(1) 已知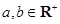 ,如果
,如果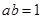 ,那么
,那么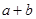 的最小值为_______;若
的最小值为_______;若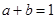 ,那么
,那么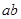 的最大值为_______.
的最大值为_______.
(2) 已知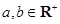 ,如果
,如果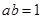 ,那么
,那么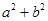 的最小值为_______;如果
的最小值为_______;如果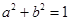 ,那么
,那么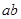 的最大值为_______.
的最大值为_______.
(3) 已知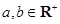 ,如果
,如果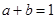 ,那么
,那么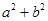 的最小值为_______;如果
的最小值为_______;如果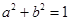 ,那么
,那么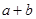 的最大值为_______.
的最大值为_______.
(4) 若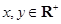 ,且
,且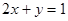 ,则
,则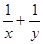 的最小值为___________.
的最小值为___________.
(5) 已知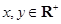 ,且
,且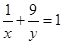 ,则
,则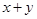 的最小值为___________.
的最小值为___________.
(6) 已知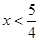 ,则函数
,则函数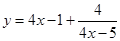 的最大值为___________.
的最大值为___________.
(7) 函数 的最大值为_____________________.
的最大值为_____________________.
(8) 已知 ,则
,则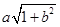 的最大值为___________.
的最大值为___________.
(9) 已知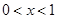 时,则
时,则 的最大值为___________.
的最大值为___________.
(10) 若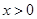 ,则函数
,则函数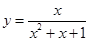 的最大值最大值为___________.
的最大值最大值为___________.
-
一元一次不等式知识点总结
四、列一元一次方程解应用题的步骤有:1、审清题意:应认真审题,分析题中的数量关系,找出问题所在。2、设未知数:用字母表示题目中的未…
-
一元一次不等式知识点总结(冀教版)
一元一次不等式(组)知识点总结不等式的概念1、不等式:用不等号(>,<,≥,≤,≠)连接的式子,叫做不等式。例如:5>2,x+y≠…
-
一元一次不等式知识点总结
一元一次不等式重点:不等式的性质和一元一次不等式的解法。难点:一元一次不等式的解法和一元一次不等式解决在现实情景下的实际问题。知识…
-
必修五-不等式知识点总结
高中数学必修5第三章不等式复习一、不等式的主要性质:(1)对称性:a?b?b?a(2)传递性:a?b,b?c?a?c(3)加法法则…
-
高考不等式知识点总结
第三章:不等式1、不等式的基本性质①(对称性)②(传递性)③(可加性)(同向可加性)(异向可减性)④(可积性)⑤(同向正数可乘性)…
-
一元一次不等式知识点总结
一元一次不等式重点:不等式的性质和一元一次不等式的解法。难点:一元一次不等式的解法和一元一次不等式解决在现实情景下的实际问题。知识…
-
一元一次不等式知识点总结(冀教版)
一元一次不等式(组)知识点总结不等式的概念1、不等式:用不等号(>,<,≥,≤,≠)连接的式子,叫做不等式。例如:5>2,x+y≠…
-
一元一次不等式知识点总结
四、列一元一次方程解应用题的步骤有:1、审清题意:应认真审题,分析题中的数量关系,找出问题所在。2、设未知数:用字母表示题目中的未…
-
平行四边形知识点总结
平行四边形知识总结及练习1.平行四边形、矩形、菱形、正方形的性质:2.识别方法小结:(1)识别平行四边形的方法:①两组对边分别平行…
-
三角形、四边形知识点总结
相交线、平行线一、相交线1.线段的垂直平分线:(1)定义:垂直且平分一条线段的直线,叫做线段的垂直平分线。(2)性质:线段垂直平分…
-
永威国际道州本土游戏总结
游戏美术包含有许多方面,所以协作,协作是做好游戏的美术的首要要素。由于游戏是交互性十分强的项目,所以,美术其实要体现企化,程序所要…