概率论与数理统计总结之第五章
第五章
大数定律
定理一(契比雪夫定理的特殊情况)
设随机变量 …
…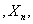 …相互独立(是指对于任意n>1,
…相互独立(是指对于任意n>1, …
…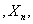 …是相互独立),且具有相同的数学期望和方差:
…是相互独立),且具有相同的数学期望和方差: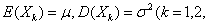 …
…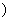 。作前n个随机变量的算术平均
。作前n个随机变量的算术平均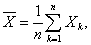
则对于任意正数ε,有
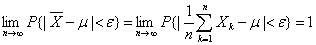
证明:
由于
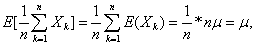
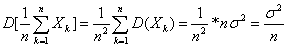 ,
,
由契比雪夫不等式可得
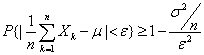
在上式中令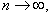 并注意到概率不能大于1,即得
并注意到概率不能大于1,即得
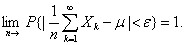
设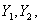 …
…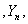 …是一个随机变量序列,a是一个常数。若对于任意正数ε,有
…是一个随机变量序列,a是一个常数。若对于任意正数ε,有
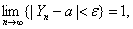
则称序列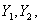 …
…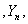 …依概率收敛与a,记为
…依概率收敛与a,记为
设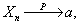
 ,又设g(x,y)在点(a,b)连续,则
,又设g(x,y)在点(a,b)连续,则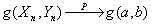
上述定理一又可叙述为:
定理一
设随机变量 …
…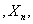 …,相互独立,且具有相同的数学期望和方差:
…,相互独立,且具有相同的数学期望和方差: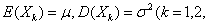 …
…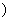 ,则序列
,则序列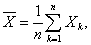 依概率收敛于μ,即
依概率收敛于μ,即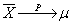
定理二(伯努利大数定理)
设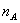 是n次独立重复试验中事件A发生的次数。p是事件A在每次试验中发生的概率,则对于任意正数ε>0,有
是n次独立重复试验中事件A发生的次数。p是事件A在每次试验中发生的概率,则对于任意正数ε>0,有
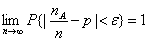 或
或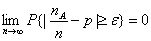
证明:
因为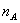 ~
~ ,有
,有
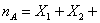 …
…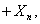
其中, …
…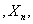 …相互独立,且都服从以p为参数的(0-1)分布,因而
…相互独立,且都服从以p为参数的(0-1)分布,因而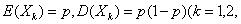 …
…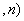 ,由定理一得
,由定理一得
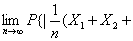 …
…
即
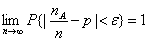
这个定理表明事件发生的频率的稳定性
定理三(辛钦定理)
设随机变量 …
…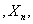 …相互独立,服从同一分布,且具有数学期望
…相互独立,服从同一分布,且具有数学期望 …
…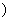 ,则对于任意正数ε,有
,则对于任意正数ε,有
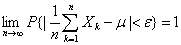
显然,伯努利大数定理是辛钦定理的特殊情况
中心极限定理
定理四(独立同分布的中心极限定理)
设随机变量 …
…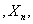 …相互独立,服从同一分布,且具有数学期望和方差:
…相互独立,服从同一分布,且具有数学期望和方差: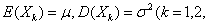 …
…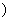 ,则随机变量之和
,则随机变量之和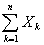 的标准化变量:
的标准化变量:
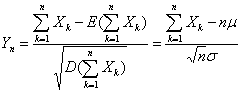
的分布函数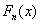 对于任意x满足
对于任意x满足

对其的解释:
 均值为μ,方差为
均值为μ,方差为
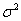 >0的独立同分布的随机变量之和
>0的独立同分布的随机变量之和
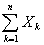 的标准化变量,当n充分大时,有
的标准化变量,当n充分大时,有
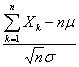 ~
~
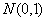
将上式左端改写成 这样上述结果可写成:
这样上述结果可写成:
当n充分大时,


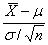 ~
~
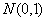 或
或
 ~
~
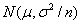
这也就是说,均值为μ,方差为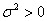 的独立同分布的随机变量
的独立同分布的随机变量 …
…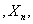 的算术平均
的算术平均 ,当n充分大时近似地服从均值为μ,方差为
,当n充分大时近似地服从均值为μ,方差为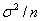 的正态分布
的正态分布
定理五(李雅普诺夫定理)
设随机变量 …
…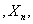 …相互独立,它们具有数学期望和方差:
…相互独立,它们具有数学期望和方差:
 …,
…,
记 ,
,
若存在正数δ,使得当 时,
时,

则随机变量之和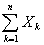 的标准化变量:
的标准化变量:

的分布函数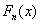 对于任意x,满足
对于任意x,满足

对其的解释为:
随机变量 ,
,
当n很大时,近似服从正态分布N(0,1),因此,当n很大时, 近似服从正态分布
近似服从正态分布
这就是说,无论各个随机变量 服从什么分布,只要满足定理的条件,那么它们的和
服从什么分布,只要满足定理的条件,那么它们的和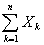 当n很大时,就近似服从正态分布
当n很大时,就近似服从正态分布
定理六(棣莫弗-拉普拉斯定理)
设随机变量 服从参数为n,p(0<p<1)的二项分布,则对于任意x,有
服从参数为n,p(0<p<1)的二项分布,则对于任意x,有

证明:
将 分解成为n个相互独立、服从同一(0-1)分布的诸随机变量
分解成为n个相互独立、服从同一(0-1)分布的诸随机变量 …
… 之和,即有
之和,即有
 =
=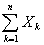 ,
,
其中 的分布律为
的分布律为

由于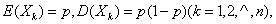 由定理四得
由定理四得

这个定理表明,正态分布是二项分布的极限分布,当n充分大时,我们可以利用定理六中的式子来计算二项分布的概率
第二篇:概率论与数理统计总结之第四章
第四章 数学期望和方差
数学期望:
设离散型随机变量X的分布律为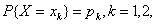 …
…
若级数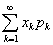 绝对收敛,则称级数
绝对收敛,则称级数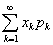 的和为随机变量X的数学期望,记为E(X),即E(X)=
的和为随机变量X的数学期望,记为E(X),即E(X)=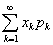
设连续型随机变量X的概率密度为f(x),
若积分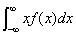 绝对收敛,则称积分
绝对收敛,则称积分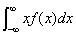 的值为随机变量X的数学期望,记为E(X),即E(X)=
的值为随机变量X的数学期望,记为E(X),即E(X)=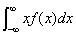
数学期望简称期望,又称为均值
数学期望E(X)完全由随机变量X的概率分布所确定,若X服从某一分布也称E(X)是这一分布的数学期望
定理
设Y是随机变量X的函数:Y=g(X)(g是连续函数)
1)X是离散型随机变量,它的分布律为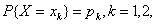 …,若
…,若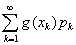 绝对收敛,则有
绝对收敛,则有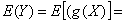
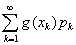
2)X是连续型随机变量,它的概率密度为f(x)。若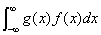 绝对收敛,则有E(Y)=E[g(X)]=
绝对收敛,则有E(Y)=E[g(X)]=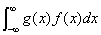
数学期望的几个重要性质:
1.设C是常数,则有E(C)=C
2.设X是一个随机变量,C是常数,则有E(CX)=CE(X)
若A,B相互独立,则有E(AB)=E(A)E(B)
3.设X,Y是两个随机变量,则有E(X+Y)=E(X)+E(Y)
方差
设X是一个随机变量,若 存在,则称
存在,则称 为X的方差,记为D(X)或Var(X),即D(X)=Var(X)=
为X的方差,记为D(X)或Var(X),即D(X)=Var(X)=
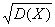 ,记为σ(X),称为标准差或均方差
,记为σ(X),称为标准差或均方差
对于离散型随机变量,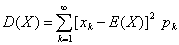
对于连续型随机变量,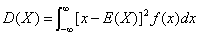
随机变量X的方差计算公式: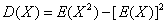
方差的几个重要性质:
1.设C是常数,则D(C)=0
2.设X是随机变量,C是常数,则有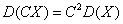
3.设X,Y是两个随机变量,则有
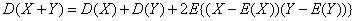
特别地,若X,Y相互独立,则有
D(X+Y)=D(X)+D(Y)
4.D(X)=0的充要条件是X以概率1取常数C,即P{X=C}=1,显然这里C=E(X)
定理:(切比雪夫不等式)
设随机变量X具有数学期望E(X)=μ,方差D(X)=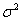 ,则对于任意正数
,则对于任意正数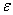 ,不等式
,不等式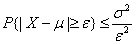 成立
成立
协方差及相关系数
量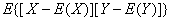 称为随机变量X与Y的协方差,记为Cov(X,Y),即
称为随机变量X与Y的协方差,记为Cov(X,Y),即
Cov(X,Y)=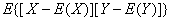
而 称为随机变量X与Y的相关系数
称为随机变量X与Y的相关系数
 是一个无量纲的量
是一个无量纲的量


协方差的性质有:
1. ,a,b是常数
,a,b是常数
2.
当| |较大时,X,Y线性相关的程度较好,当|
|较大时,X,Y线性相关的程度较好,当| |较小时,X,Y线性相关的程度较差,当
|较小时,X,Y线性相关的程度较差,当 =0,称X和Y不相关
=0,称X和Y不相关
若X,Y独立,则其不相关,但若X,Y不相关,并不能说明其独立
矩、协方差矩阵
设X,Y是随机变量,若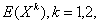 …存在,称它为X的k阶原点矩,简称k阶矩
…存在,称它为X的k阶原点矩,简称k阶矩
若 …存在,称它为X的k阶中心矩
…存在,称它为X的k阶中心矩
若 …存在,称它为X和Y的k+l阶混合矩
…存在,称它为X和Y的k+l阶混合矩
若 …存在,称它为X和Y的k+l阶混合中心矩
…存在,称它为X和Y的k+l阶混合中心矩
设n维随机变量 …
… 的二阶混合中心矩
的二阶混合中心矩
 …
…
都存在,则称矩阵

为n维随机变量 …
… 的协方差矩阵
的协方差矩阵
由于 ,因而上述矩阵是一个对称矩阵
,因而上述矩阵是一个对称矩阵
第三篇:概率论与数理统计知识点总结(详细)
《概率论与数理统计》
第一章 概率论的基本概念
§2.样本空间、随机事件
1.事件间的关系 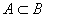 则称事件B包含事件A,指事件A发生必然导致事件B发生
则称事件B包含事件A,指事件A发生必然导致事件B发生
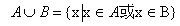 称为事件A与事件B的和事件,指当且仅当A,B中至少有一个发生时,事件
称为事件A与事件B的和事件,指当且仅当A,B中至少有一个发生时,事件 发生
发生
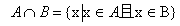 称为事件A与事件B的积事件,指当A,B同时发生时,事件
称为事件A与事件B的积事件,指当A,B同时发生时,事件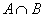 发生
发生
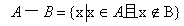 称为事件A与事件B的差事件,指当且仅当A发生、B不发生时,事件
称为事件A与事件B的差事件,指当且仅当A发生、B不发生时,事件 发生
发生
 ,则称事件A与B是互不相容的,或互斥的,指事件A与事件B不能同时发生,基本事件是两两互不相容的
,则称事件A与B是互不相容的,或互斥的,指事件A与事件B不能同时发生,基本事件是两两互不相容的
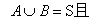
 ,则称事件A与事件B互为逆事件,又称事件A与事件B互为对立事件
,则称事件A与事件B互为逆事件,又称事件A与事件B互为对立事件
2.运算规则 交换律
结合律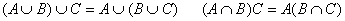
分配律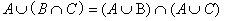
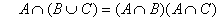
徳摩根律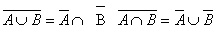
§3.频率与概率
定义 在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的次数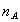 称为事件A发生的频数,比值
称为事件A发生的频数,比值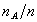 称为事件A发生的频率
称为事件A发生的频率
概率:设E是随机试验,S是它的样本空间,对于E的每一事件A赋予一个实数,记为P(A),称为事件的概率
1.概率 满足下列条件:
满足下列条件:
(1)非负性:对于每一个事件A 
(2)规范性:对于必然事件S 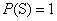
(3)可列可加性:设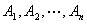 是两两互不相容的事件,有
是两两互不相容的事件,有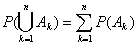 (
( 可以取
可以取 )
)
2.概率的一些重要性质:
(i)
(ii)若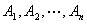 是两两互不相容的事件,则有
是两两互不相容的事件,则有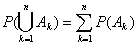 (
( 可以取
可以取 )
)
(iii)设A,B是两个事件若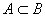 ,则
,则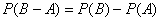 ,
,
(iv)对于任意事件A,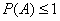
(v) (逆事件的概率)
(逆事件的概率)
(vi)对于任意事件A,B有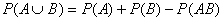
§4等可能概型(古典概型)
等可能概型:试验的样本空间只包含有限个元素,试验中每个事件发生的可能性相同
若事件A包含k个基本事件,即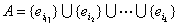 ,里
,里
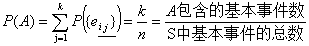
§5.条件概率
(1) 定义:设A,B是两个事件,且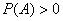 ,称
,称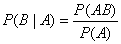 为事件A发生的条件下事件B发生的条件概率
为事件A发生的条件下事件B发生的条件概率
(2) 条件概率符合概率定义中的三个条件
1。非负性:对于某一事件B,有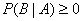
2。规范性:对于必然事件S,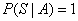
3可列可加性:设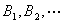 是两两互不相容的事件,则有
是两两互不相容的事件,则有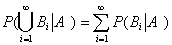
(3) 乘法定理 设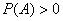 ,则有
,则有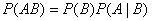 称为乘法公式
称为乘法公式
(4) 全概率公式: 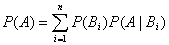
贝叶斯公式:
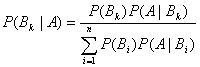
§6.独立性
定义 设A,B是两事件,如果满足等式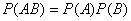 ,则称事件A,B相互独立
,则称事件A,B相互独立
定理一 设A,B是两事件,且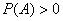 ,若A,B相互独立,则
,若A,B相互独立,则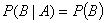
定理二 若事件A和B相互独立,则下列各对事件也相互独立:A与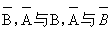
第二章 随机变量及其分布
§1随机变量
定义 设随机试验的样本空间为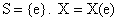 是定义在样本空间S上的实值单值函数,称
是定义在样本空间S上的实值单值函数,称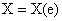 为随机变量
为随机变量
§2离散性随机变量及其分布律
1. 离散随机变量:有些随机变量,它全部可能取到的值是有限个或可列无限多个,这种随机变量称为离散型随机变量
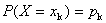 满足如下两个条件(1)
满足如下两个条件(1)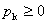 ,(2)
,(2)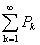 =1
=1
2. 三种重要的离散型随机变量
(1)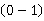 分布
分布
设随机变量X只能取0与1两个值,它的分布律是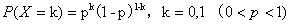 ,则称X服从以p为参数的
,则称X服从以p为参数的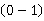 分布或两点分布。
分布或两点分布。
(2)伯努利实验、二项分布
设实验E只有两个可能结果:A与 ,则称E为伯努利实验.设
,则称E为伯努利实验.设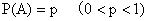 ,此时
,此时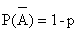 .将E独立重复的进行n次,则称这一串重复的独立实验为n重伯努利实验。
.将E独立重复的进行n次,则称这一串重复的独立实验为n重伯努利实验。
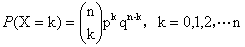 满足条件(1)
满足条件(1)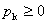 ,(2)
,(2)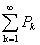 =1注意到
=1注意到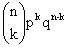 是二项式
是二项式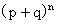 的展开式中出现
的展开式中出现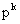 的那一项,我们称随机变量X服从参数为n,p的二项分布。
的那一项,我们称随机变量X服从参数为n,p的二项分布。
(3)泊松分布
设随机变量X所有可能取的值为0,1,2…,而取各个值的概率为
 其中
其中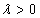 是常数,则称X服从参数为
是常数,则称X服从参数为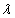 的泊松分布记为
的泊松分布记为
§3随机变量的分布函数
定义 设X是一个随机变量,x是任意实数,函数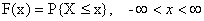
称为X的分布函数
分布函数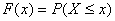 ,具有以下性质(1)
,具有以下性质(1) 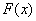 是一个不减函数 (2)
是一个不减函数 (2)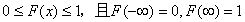 (3)
(3)
§4连续性随机变量及其概率密度
连续随机变量:如果对于随机变量X的分布函数F(x),存在非负可积函数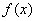 ,使对于任意函数x有
,使对于任意函数x有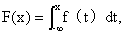 则称x 为连续性随机变量,其中函数f(x)称为X的概率密度函数,简称概率密度
则称x 为连续性随机变量,其中函数f(x)称为X的概率密度函数,简称概率密度
1 概率密度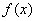 具有以下性质,满足(1)
具有以下性质,满足(1) ;
;
(3)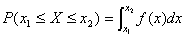 ;(4)若
;(4)若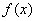 在点x处连续,则有
在点x处连续,则有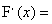
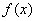
2,三种重要的连续型随机变量
(1)均匀分布
若连续性随机变量X具有概率密度 ,则成X在区间(a,b)上服从均匀分布.记为
,则成X在区间(a,b)上服从均匀分布.记为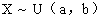
(2)指数分布
若连续性随机变量X的概率密度为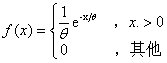 其中
其中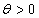 为常数,则称X服从参数为
为常数,则称X服从参数为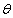 的指数分布。
的指数分布。
(3)正态分布
若连续型随机变量X的概率密度为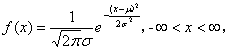
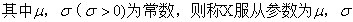 的正态分布或高斯分布,记为
的正态分布或高斯分布,记为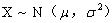
特别,当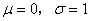 时称随机变量X服从标准正态分布
时称随机变量X服从标准正态分布
§5随机变量的函数的分布
定理 设随机变量X具有概率密度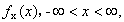 又设函数
又设函数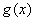 处处可导且恒有
处处可导且恒有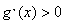 ,则Y=
,则Y=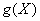 是连续型随机变量,其概率密度为
是连续型随机变量,其概率密度为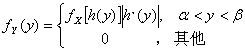
第三章 多维随机变量
§1二维随机变量
定义 设E是一个随机试验,它的样本空间是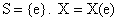 和
和 是定义在S上的随机变量,称
是定义在S上的随机变量,称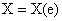 为随机变量,由它们构成的一个向量(X,Y)叫做二维随机变量
为随机变量,由它们构成的一个向量(X,Y)叫做二维随机变量
设(X,Y)是二维随机变量,对于任意实数x,y,二元函数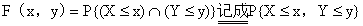 称为二维随机变量(X,Y)的分布函数
称为二维随机变量(X,Y)的分布函数
如果二维随机变量(X,Y)全部可能取到的值是有限对或可列无限多对,则称(X,Y)是离散型的随机变量。
我们称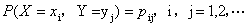 为二维离散型随机变量(X,Y)的分布律。
为二维离散型随机变量(X,Y)的分布律。
对于二维随机变量(X,Y)的分布函数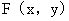 ,如果存在非负可积函数f(x,y),使对于任意x,y有
,如果存在非负可积函数f(x,y),使对于任意x,y有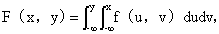 则称(X,Y)是连续性的随机变量,函数f(x,y)称为随机变量(X,Y)的概率密度,或称为随机变量X和Y的联合概率密度。
则称(X,Y)是连续性的随机变量,函数f(x,y)称为随机变量(X,Y)的概率密度,或称为随机变量X和Y的联合概率密度。
§2边缘分布
二维随机变量(X,Y)作为一个整体,具有分布函数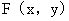 .而X和Y都是随机变量,各自也有分布函数,将他们分别记为
.而X和Y都是随机变量,各自也有分布函数,将他们分别记为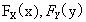 ,依次称为二维随机变量(X,Y)关于X和关于Y的边缘分布函数。
,依次称为二维随机变量(X,Y)关于X和关于Y的边缘分布函数。
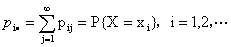
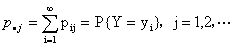 分别称
分别称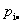
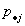 为(X,Y)关于X和关于Y的边缘分布律。
为(X,Y)关于X和关于Y的边缘分布律。
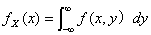
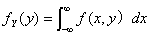 分别称
分别称 ,
,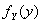 为X,Y关于X和关于Y的边缘概率密度。
为X,Y关于X和关于Y的边缘概率密度。
§3条件分布
定义 设(X,Y)是二维离散型随机变量,对于固定的j,若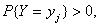
则称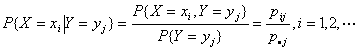 为在
为在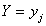 条件下随机变量X的条件分布律,同样
条件下随机变量X的条件分布律,同样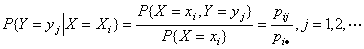 为在
为在 条件下随机变量X的条件分布律。
条件下随机变量X的条件分布律。
设二维离散型随机变量(X,Y)的概率密度为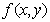 ,(X,Y)关于Y的边缘概率密度为
,(X,Y)关于Y的边缘概率密度为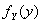 ,若对于固定的y,
,若对于固定的y,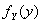 〉0,则称
〉0,则称 为在Y=y的条件下X的条件概率密度,记为
为在Y=y的条件下X的条件概率密度,记为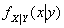 =
=
§4相互独立的随机变量
定义 设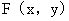 及
及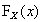 ,
,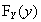 分别是二维离散型随机变量(X,Y)的分布函数及边缘分布函数.若对于所有x,y有
分别是二维离散型随机变量(X,Y)的分布函数及边缘分布函数.若对于所有x,y有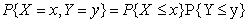 ,即
,即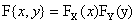 ,则称随机变量X和Y是相互独立的。
,则称随机变量X和Y是相互独立的。
对于二维正态随机变量(X,Y),X和Y相互独立的充要条件是参数
§5两个随机变量的函数的分布
1,Z=X+Y的分布
设(X,Y)是二维连续型随机变量,它具有概率密度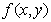 .则Z=X+Y仍为连续性随机变量,其概率密度为
.则Z=X+Y仍为连续性随机变量,其概率密度为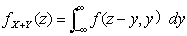 或
或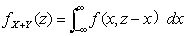
又若X和Y相互独立,设(X,Y)关于X,Y的边缘密度分别为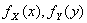 则
则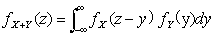 和
和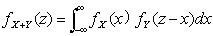 这两个公式称为
这两个公式称为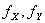 的卷积公式
的卷积公式
有限个相互独立的正态随机变量的线性组合仍然服从正态分布
2,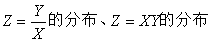
设(X,Y)是二维连续型随机变量,它具有概率密度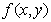 ,则
,则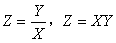
仍为连续性随机变量其概率密度分别为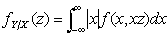
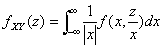 又若X和Y相互独立,设(X,Y)关于X,Y的边缘密度分别为
又若X和Y相互独立,设(X,Y)关于X,Y的边缘密度分别为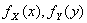 则可化为
则可化为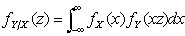
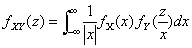
3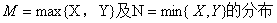
设X,Y是两个相互独立的随机变量,它们的分布函数分别为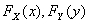 由于
由于 不大于z等价于X和Y都不大于z故有
不大于z等价于X和Y都不大于z故有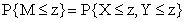 又由于X和Y相互独立,得到
又由于X和Y相互独立,得到 的分布函数为
的分布函数为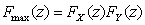
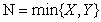 的分布函数为
的分布函数为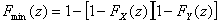
第四章 随机变量的数字特征
§1.数学期望
定义 设离散型随机变量X的分布律为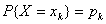 ,k=1,2,…若级数
,k=1,2,…若级数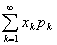 绝对收敛,则称级数
绝对收敛,则称级数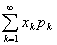 的和为随机变量X的数学期望,记为
的和为随机变量X的数学期望,记为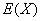 ,即
,即
设连续型随机变量X的概率密度为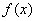 ,若积分
,若积分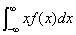 绝对收敛,则称积分
绝对收敛,则称积分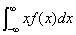 的值为随机变量X的数学期望,记为
的值为随机变量X的数学期望,记为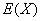 ,即
,即
定理 设Y是随机变量X的函数Y=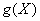 (g是连续函数)
(g是连续函数)
(i)如果X是离散型随机变量,它的分布律为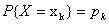 ,k=1,2,…若
,k=1,2,…若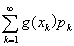 绝对收敛则有
绝对收敛则有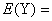
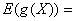
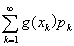
(ii)如果X是连续型随机变量,它的分概率密度为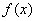 ,若
,若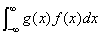 绝对收敛则有
绝对收敛则有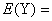
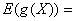
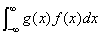
数学期望的几个重要性质
1设C是常数,则有
2设X是随机变量,C是常数,则有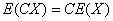
3设X,Y是两个随机变量,则有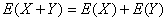 ;
;
4设X,Y是相互独立的随机变量,则有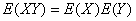
§2方差
定义 设X是一个随机变量,若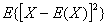 存在,则称
存在,则称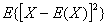 为X的方差,记为D(x)即D(x)=
为X的方差,记为D(x)即D(x)=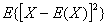 ,在应用上还引入量
,在应用上还引入量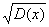 ,记为
,记为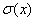 ,称为标准差或均方差。
,称为标准差或均方差。
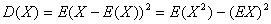
方差的几个重要性质
1设C是常数,则有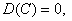
2设X是随机变量,C是常数,则有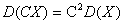 ,
,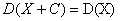
3设X,Y是两个随机变量,则有 特别,若X,Y相互独立,则有
特别,若X,Y相互独立,则有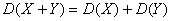
4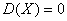 的充要条件是X以概率1取常数
的充要条件是X以概率1取常数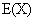 ,即
,即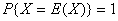
切比雪夫不等式:设随机变量X具有数学期望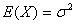 ,则对于任意正数
,则对于任意正数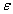 ,不等式
,不等式 成立
成立
§3协方差及相关系数
定义 量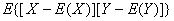 称为随机变量X与Y的协方差为
称为随机变量X与Y的协方差为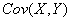 ,即
,即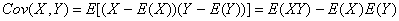
而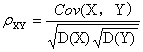 称为随机变量X和Y的相关系数
称为随机变量X和Y的相关系数
对于任意两个随机变量X 和Y,
协方差具有下述性质
1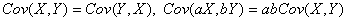
2
定理 1 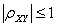
2  的充要条件是,存在常数a,b使
的充要条件是,存在常数a,b使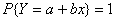
当
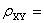 0时,称X和Y不相关
0时,称X和Y不相关
附:几种常用的概率分布表

第五章大数定律与中心极限定理
§1.大数定律
弱大数定理(辛欣大数定理) 设X1,X2…是相互独立,服从统一分布的随机变量序列,并具有数学期望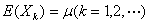 .作前n个变量的算术平均
.作前n个变量的算术平均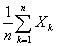 ,则对于任意
,则对于任意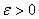 ,有
,有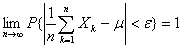
定义 设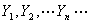 是一个随机变量序列,a是一个常数,若对于任意正数
是一个随机变量序列,a是一个常数,若对于任意正数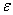 ,有
,有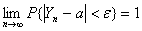 ,则称序列
,则称序列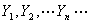 依概率收敛于a,记为
依概率收敛于a,记为
伯努利大数定理 设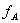 是n次独立重复试验中事件A发生的次数,p是事件A在每次试验中发生的概率,则对于任意正数
是n次独立重复试验中事件A发生的次数,p是事件A在每次试验中发生的概率,则对于任意正数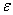 〉0,有
〉0,有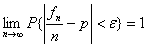 或
或
§2中心极限定理
定理一(独立同分布的中心极限定理) 设随机变量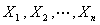 相互独立,服从同一分布,且具有数学期望和方差
相互独立,服从同一分布,且具有数学期望和方差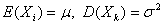 (k=1,2,…),则随机变量之和
(k=1,2,…),则随机变量之和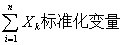 ,
, 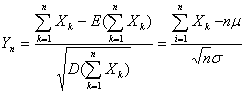 ,
,
定理二(李雅普诺夫定理) 设随机变量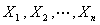 …相互独立,它们具有数学期望和方差
…相互独立,它们具有数学期望和方差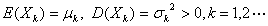 记
记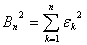
定理三(棣莫弗-拉普拉斯定理)设随机变量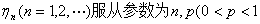 )的二项分布,则对任意
)的二项分布,则对任意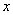 ,有
,有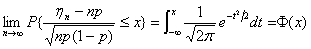
-
概率论与数理统计知识点总结(详细)
概率论与数理统计第一章概率论的基本概念2样本空间随机事件1事件间的关系AB则称事件B包含事件A指事件A发生必然导致事件B发生ABx…
-
高中数学概率统计知识点总结
一、抽样方法1.简单随机抽样2.简单随机抽样常用的方法:(1)抽签法;⑵随机数表法。3.系统抽样:K(抽样距离)=N(总体规模)/…
-
概率论与数理统计知识点总结(免费)
概率论与数理统计第一章概率论的基本概念2样本空间随机事件1事件间的关系AB则称事件B包含事件A指事件A发生必然导致事件B发生ABx…
-
概率论与数理统计知识点总结(详细)
概率论与数理统计第一章概率论的基本概念22样本空间随机事件24等可能概型古典概型35条件概率46独立性4第二章随机变量及其分布51…
-
20xx中考概率和统计知识点总结
统计初步与概率初步考点一、平均数1、平均数的概念(1)平均数:一般地,如果有n个数x1,x2,?,xn,那么,x?的平均数,x读作…
-
《农村统计》总结报告
《农村统计》课程改革总结报告一、任务基本情况依据重庆三峡职业学院《重庆市示范性高等职业院校项目建设方案》和《重庆市示范性高等职业院…
-
20xx宁源统计总结
宁强县能源统计工作总结20xx年我县能源统计工作在县委、县政府的正确领导下,在省、市统计局的指导和大力支持下,认真贯彻落实国家和省…
-
20xx年博湖中学国防教育工作总结
20xx学年,博湖中学在上级部门的领导下,认真落实国防教育工作的文件精神,围绕新时期国防教育特点,把国防教育与爱国教育相结合,通过…
-
小学知识产权教育工作总结
柯坪县第二小学知识产权教育工作汇报材料我校始终认真落实阿克苏地区关于知识产权教育工作的文件精神,本着教育一个学生,影响一个家庭,带…
-
20xx年财政同步监督工作总结
20xx年我所在县局的领导下,在相关股、室的指导下,本着强化财政监督,提高财政科学化精细化管理工作水平。按照财政同步监督工作方案的…