高一数学集合小结与复习
集合小结与复习课
【学习导航】
知识网络
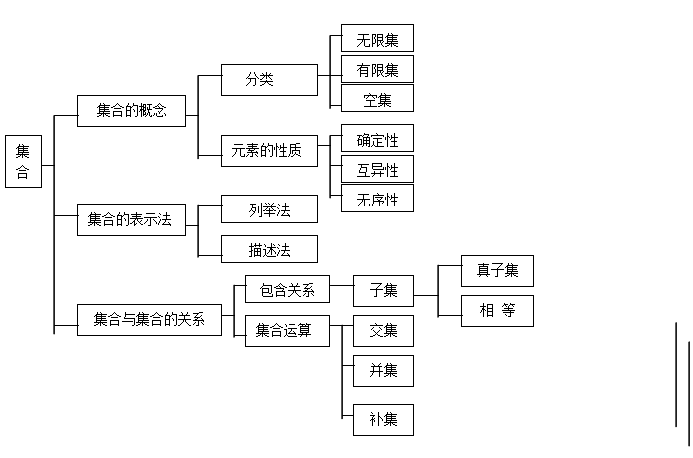
1.以集合为中心的知识网络概述
集合是高中数学的基础,也是高考中常考的内容之一.集合思想及集合语言可以渗透到高中数学的各个分支,它可与函数、方程和不等式等许多知识综合起来进行考查.在解题时首先需要我们能读懂集合语言,将集合语言转换为数学语言,再用相关的知识解决问题.
2.对集合中元素三大性质的理解
(1)确定性
集合中的元素,必须是确定的.对于集合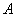 和元素
和元素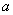 ,要么
,要么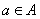 ,要么
,要么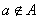 ,二者必居其一.比如:“所有大于100的数”组成一个集合,集合中的元素是确定的.而“较大的整数”就不能构成一个集合,因为它的对象是不确定的.再如,“较大的树”、“较高的人”等都不能构成集合.
,二者必居其一.比如:“所有大于100的数”组成一个集合,集合中的元素是确定的.而“较大的整数”就不能构成一个集合,因为它的对象是不确定的.再如,“较大的树”、“较高的人”等都不能构成集合.
(2)互异性
对于一个给定的集合,集合中的元素一定是不同的.任何两个相同的对象在同一集合中时,只能算作这个集合中的一个元素.如:由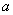 ,
,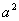 组成一个集合,则
组成一个集合,则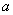 的取值不能是
的取值不能是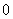 或1.
或1.
(3)无序性
集合中的元素的次序无先后之分.如:由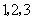 组成一个集合,也可以写成
组成一个集合,也可以写成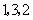 组成一个集合,它们都表示同一个集合.
组成一个集合,它们都表示同一个集合.
3.学习集合表示方法时应注意的问题
(1)注意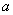 与
与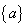 的区别.
的区别.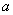 是集合
是集合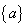 的一个元素,而
的一个元素,而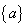 是含有一个元素
是含有一个元素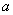 的集合,二者的关系是
的集合,二者的关系是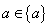 .
.
(2)注意 与
与 的区别.
的区别. 是不含任何元素的集合,而
是不含任何元素的集合,而 是含有元素
是含有元素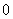 的集合.
的集合.
(3)在用列举法表示集合时,一定不能犯用{实数集}或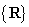 来表示实数集
来表示实数集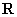 这一类错误,因为这里“大括号”已包含了“所有”的意思.
这一类错误,因为这里“大括号”已包含了“所有”的意思.
用特征性质描述法表示集合时,要特别注意这个集合中的元素是什么,它应具备哪些特征性质,从而准确地理解集合的意义.例如:
集合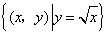 中的元素是
中的元素是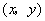 ,这个集合表示二元方程
,这个集合表示二元方程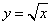 的解集,或者理解为曲线
的解集,或者理解为曲线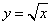 上的点组成的点集;
上的点组成的点集;
集合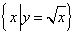 中的元素是
中的元素是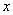 ,这个集合表示函数
,这个集合表示函数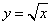 中自变量
中自变量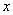 的取值范围;
的取值范围;
集合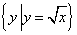 中的元素是
中的元素是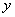 ,这个集合表示函数
,这个集合表示函数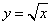 中函数值
中函数值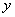 的取值范围;
的取值范围;
集合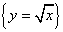 中的元素只有一个(方程
中的元素只有一个(方程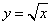 ),它是用列举法表示的单元素集合.
),它是用列举法表示的单元素集合.
4.集合间的关系及集合运算问题点评
(1)要注意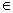 与
与 间的区别:“
间的区别:“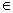 ”表示元素与集合间的关系,如
”表示元素与集合间的关系,如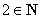 .“
.“ ”表示集合与集合间的关系,如
”表示集合与集合间的关系,如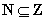 .
.
(2)理解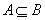 与
与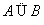 的含义:“
的含义:“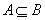 ”包含“
”包含“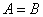 ”,“
”,“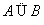 ”两种情况,其中必有一种且只有一种情况成立;而“
”两种情况,其中必有一种且只有一种情况成立;而“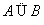 ”等价于“
”等价于“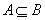 且
且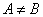 ”.
”.
(3)尝试用Venn图表示两个集合间的关系,并逐步形成用集合的观点去认识问题、思考问题的思维方式.学会分类写出给定集合的所有子集的解题技巧,并通过对教材“探索与研究”中习题的探究,找出集合中元素的个数与它的所有子集个数的关系规律.
(4)交集、并集、全集、补集的定义及其运算是本部分的重点,可以结合Venn图去理解并且应当重视Venn图的直观作用.
(5)应重视利用空集的特性.空集是一个特殊的集合,它是任何集合的子集,利用空集的这一特性,可使一些题设中隐含有空集条件的问题得以正确解决.
(6)补集思想在集合运算中的作用也是不可忽视的.对于一个问题,如果正面去求解比较困难,则可以从这个问题的反面入手,也就是采用补集的思想.
自学评价
1.对于集合的问题:要确定属于哪一类集合(数集,点集,或某类图形集),然后再确定处理此类问题的方法.
2.关于集合中的运算,一般应把各参与运算的集合化到最简形式,然后再进行运算.
3.含参数的集合问题,多根据集合的的互异性处理,有时需要用到分类讨论、数形集结合的思想.
4.集合问题多与函数、方程有关,要注意
各类知识的融会贯通.
【精典范例】
例1. 设U={1,2,3,4,5},且A∩B={2},
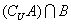 ={4},
={4},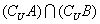
={1,5},则下列结论正确的是
( )
A.3∈A,3∈B
B.2∈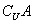 ,3∈B
,3∈B
 C.3∈
C.3∈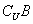 ,3∈A
,3∈A
D.3∈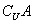 ,3∈
,3∈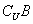
分析:按题意画出Venn图即可找出选择
的分支.
【解】
画出满题意足Venn图:
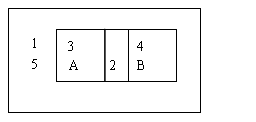
由图可知:3∈A且3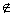 B,即3∈A且
B,即3∈A且
3∈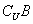 , ∴ 选C.
, ∴ 选C.
点评:
本题可用排除法来解,若选A,则3∈
A∩B,与已知A∩B={2}矛盾,……显然这种方法没有Venn图形象直观,这也突出数形集结合的思想在集合中的运用.
追踪训练一
1. 设U={x|0+},若A∩B={3},
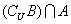 ={1,5,7},
={1,5,7},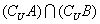
={9},求集合A,B.
【解】
A={1,3,5,7},
B={2,3,4,6,8}.
2.某校有A、B两项课外科技制作小组,50名学生中报名参加A组的人数是全体学生人数的3/5,报名参加B组的人数比报名参加A组的人数多3人,两组都没有报名的人数是同时报名的人数的1/3还多1人,求同时报名参加A、B两组人数及两组都没有报名的人数.
【解】
同时报名参加A、B组的人数为21人,
两组都没有报名的人数为8人.
例2:已知全集U=R,集合A={x|x2-x-6<0},
B={x|x2+2x-8>0},C={x|x2-4ax+3a2<0},
(1)试求a的取值范围,使A∩B C;
C;
(2)试求a的取值范围,使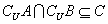
分析:
U=R,A=(-2,3),B=(-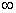 ,-4)∪(2,+
,-4)∪(2,+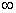 ),故A∩B=(2,3),
),故A∩B=(2,3),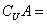
(-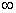 ,-2]∪[3,+
,-2]∪[3,+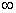 ),
),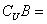 [-4,2],
[-4,2],
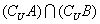 =[-4,-2],
=[-4,-2],
x2-4ax+3a2<0即(x-3a)(x-a)<0,
∴当a<0时,C=(3a,a),
当a=0时,C= ,
,
当a>0时,C=(a,3a),
(1) 要使A∩B C,集合数轴知,
C,集合数轴知,
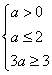 解得 1≤a≤2;
解得 1≤a≤2;
(2) 类似地,要使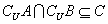 必有
必有
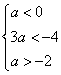 解得
解得 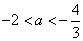
【解】
解答过程只需要将上面的分析整理一下
即可.
点评:
①研究不等式的解集的包含关系或进行集
合的运算时,充分利用数轴的直观性,便
于分析与转化.
②注意分类讨论的思想在解题中的运用,在
分类时要满足不重复、不遗漏的原则.
追踪训练二
1. 设A={x|x2-x-2<0},B={x||x|=y+1,y∈A},
求:
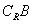 ,A∪B,A∩
,A∪B,A∩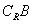 ,
,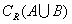
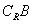 ∩
∩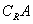
【解】
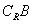 =(-
=(-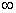 ,-3]∪[3,+
,-3]∪[3,+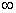 )∪{0};
)∪{0};
A∪B=(-3,3);
A∩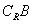 ={0};
={0};
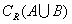 =(-
=(-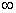 ,-3]∪[3,+
,-3]∪[3,+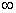 ).
).
2. 已知A={x|-x2+3x+10≥0},
B={x|m≤x≤2 m -1},若B A,
A,
求实数m的取值范围.
【解】
实数m的取值范围:(-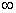 , 3) .
, 3) .
例3: 已知集合A={x|x2+4ax-4a+3=0},
B={x|x2+(a-1)x+a2=0},C={x|x2+2ax-2a=0},
其中至少有一个集合不是空集,求实数a
的取值范围.
分析:
此题若从正面入手,要对七种可能情况逐
一进行讨论,相当繁琐;若考虑其反面,则
只有一种情况,即三个集合全是空集.
【解】 当三个集合全是空集时,所以对应的三个方程都没有实数解,
即
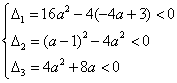
解此不等式组,得
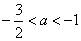
∴所求实数a的取值范围为:
a≤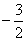 ,或a≥-1.
,或a≥-1.
点评:
采用“正难则反”的解题策略,具体地说,
就是将所研究的对象的全体视为全集,求
出使问题反面成立的集合,那么这个集合
的补集便为所求.
第二篇:高一数学集合知识点总结
一.知识归纳:
1.集合的有关概念。
1)集合(集):某些指定的对象集在一起就成为一个集合(集).其中每一个对象叫元素 注意:①集合与集合的元素是两个不同的概念,教科书中是通过描述给出的,这与平面几何中的点与直线的概念类似。
②集合中的元素具有确定性(a?A和a?A,二者必居其一)、互异性(若a?A,b?A,则a≠b)和无序性({a,b}与{b,a}表示同一个集合)。
③集合具有两方面的意义,即:凡是符合条件的对象都是它的元素;只要是它的元素就必须符号条件
2)集合的表示方法:常用的有列举法、描述法和图文法
3)集合的分类:有限集,无限集,空集。
4)常用数集:N,Z,Q,R,N*
2.子集、交集、并集、补集、空集、全集等概念。
1)子集:若对x∈A都有x∈B,则A B(或A B);
2)真子集:A B且存在x0∈B但x0 A;记为A B(或 ,且 )
3)交集:A∩B={x| x∈A且x∈B}
4)并集:A∪B={x| x∈A或x∈B}
5)补集:CUA={x| x A但x∈U}
注意:①? A,若A≠?,则? A ;
②若 , ,则 ;
③若 且 ,则A=B(等集)
3.弄清集合与元素、集合与集合的关系,掌握有关的术语和符号,特别要注意以下的符号:(1) 与 、?的区别;(2) 与 的区别;(3) 与 的区别。
4.有关子集的几个等价关系
①A∩B=A A B;②A∪B=B A B;③A B C uA C uB;
④A∩CuB = 空集 CuA B;⑤CuA∪B=I A B。
5.交、并集运算的性质
①A∩A=A,A∩? = ?,A∩B=B∩A;②A∪A=A,A∪? =A,A∪B=B∪A; ③Cu (A∪B)= CuA∩CuB,Cu (A∩B)= CuA∪CuB;
6.有限子集的个数:设集合A的元素个数是n,则A有2n个子集,2n-1个非空子集,2n-2个非空真子集。
二.例题讲解:
【例1】已知集合M={x|x=m+ ,m∈Z},N={x|x= ,n∈Z},P={x|x= ,p∈Z},则M,N,P满足关系
A) M=N P B) M N=P C) M N P D) N P M
分析一:从判断元素的共性与区别入手。
解答一:对于集合M:{x|x= ,m∈Z};对于集合N:{x|x= ,n∈Z}
对于集合P:{x|x= ,p∈Z},由于3(n-1)+1和3p+1都表示被3除余1的数,而6m+1表示被6除余1的数,所以M N=P,故选B。
分析二:简单列举集合中的元素。
解答二:M={…, ,…},N={…, , , ,…},P={…, , ,…},这时不要急于判断三个集合间的关系,应分析各集合中不同的元素。
= ∈N, ∈N,∴M N,又 = M,∴M N,
= P,∴N P 又 ∈N,∴P N,故P=N,所以选B。
点评:由于思路二只是停留在最初的归纳假设,没有从理论上解决问题,因此提倡思路一,但思路二易人手。
变式:设集合 , ,则( B )
A.M=N B.M N C.N M D.
解:
当 时,2k+1是奇数,k+2是整数,选B
【例2】定义集合A*B={x|x∈A且x B},若A={1,3,5,7},B={2,3,5},则A*B的子集个数为
A)1 B)2 C)3 D)4
分析:确定集合A*B子集的个数,首先要确定元素的个数,然后再利用公式:集合A={a1,a2,…,an}有子集2n个来求解。
解答:∵A*B={x|x∈A且x B}, ∴A*B={1,7},有两个元素,故A*B的子集共有22个。选D。
变式1:已知非空集合M {1,2,3,4,5},且若a∈M,则6?a∈M,那么集合M的个数为
A)5个 B)6个 C)7个 D)8个
变式2:已知{a,b} A {a,b,c,d,e},求集合A.
解:由已知,集合中必须含有元素a,b.
集合A可能是{a,b},{a,b,c},{a,b,d},{a,b,e},{a,b,c,d},{a,b,c,e},{a,b,d,e}. 评析 本题集合A的个数实为集合{c,d,e}的真子集的个数,所以共有 个 .
-
初中数学学习心得体会
数学是一们基础学科,我们从小学就开始接触到它。初中数学对知识的难度、深度、广度要求更高,有一部分同学由于不适应这种变化,数学成绩总…
-
数学学习总结
这次国培,我的感悟很多,也思考很多原来不曾想过的问题,同时收获也很多。“国培”期间,每一位专家们精彩的讲演,都使我很感动;他们结合…
-
数学学习总结
学习数学的意义数学有其内在的价值和意义,数学学习赋予了一个人成长意义上的本质力量。数学学习强烈而深远地影响着自我认识,数学跟语文不…
-
学习数学心得体会[1]
事只怕有心人我们每一个人都应认真对待平时的习惯不养好以后就会错误百出判案高手宋慈因一时疏忽造成了冤假错案的发生那更何况是我们呢所以…
-
高中数学学习心得体会
高中数学,可能对于某些人来说是一门头疼的课程。现在,我以毕业多年的身份来谈谈高中数学的学习心得体会,可能说法有些偏颇,但是都是我的…
-
高一数学集合与函数知识点总结
高中课程复习专题——数学集合与函数专题一、集合相关概念1、集合中元素的特性⑴元素的确定性:组成集合的元素必须是确定的。⑵元素的互异…
-
高一数学必修1第一章知识点总结
一、集合有关概念1.集合的含义2.集合的中元素的三个特性:(1)元素的确定性,(2)元素的互异性,(3)元素的无序性,3.集合的表…
-
高一数学知识点归纳总结
高中高一数学必修1各章知识点总结第一章集合与函数概念一、集合有关概念1、集合的含义:某些指定的对象集在一起就成为一个集合,其中每一…
-
《集合》知识点总结
一、集合有关概念1.集合的含义一般地,把研究对象统称为元素,把一些元素组成的总体叫做集合(简称为集)2.集合中元素的三个特性:确定…
-
高一数学集合符号总结
高一集合符号总结定范围的,确定的,可以区别的事物,当作一个整体来看待,就叫做集合,简称集,其中各事物叫做集合的元素或简称元。任何集…