双曲线知识点归纳总结
第二章 2.3 双曲线
① 当|MF1|-|MF2|=2a时,则表示点M在双曲线右支上; 当MF?MF?2a时,则表示点M在双曲线左支上;
2
1
② 注意定义中的“(小于F1F2)”这一限制条件,其根据是“三角形两边之和之差小于第三边”。
若2a=2c时,即MF?MF
1
2
?F1F2
2
,当MF
1
?MF2?F1F2
,动点轨迹是以F2为端点向
右延伸的一条射线;当MF
?MF1?F1F2
时,动点轨迹是以F1为端点向左延伸的一
条射线;
若2a>2c时,动点轨迹不存在. 2. 双曲线的标准方程判别方法是:
如果x2项的系数是正数,则焦点在x轴上; 如果y2项的系数是正数,则焦点在y轴上.
对于双曲线,a不一定大于b,因此不能像椭圆那样,通过比较分母的大小来判断焦点在哪一条坐标轴上. 3. 双曲线的内外部 (1)点P(x0,y0)在双曲线 (2)点P(x0,y0)在双曲线
xaxa
2222
??
ybyb
2222
?1(a?0,b?0)的内部??1(a?0,b?0)的外部?
x0aax0
2222
??
y0bby0
2
22
?1. ?1.
2
4. 形如Ax?By?1(AB?0)的方程可化为
2
2
x
2
1A
?
y
2
1B
?1
当当
1A1A
?0,?0,
1B1B
?0,双曲线的焦点在y轴上; ?0,双曲线的焦点在x轴上;
5.求双曲线的标准方程,
应注意两个问题:⑴ 正确判断焦点的位置;⑵ 设出标准方程后,运用待定系数法求解.
6. 离心率与渐近线之间的关系
e?
2
ca
22
?
a?ba
2
22
?1?
2
ba
22
ba
22
1)e?
?b?1???
?a?
2)
?
e?1
2
7. 双曲线的方程与渐近线方程的关系 (1)若双曲线方程为
xa
22
?
ba
yb
22
?1?渐近线方程:
xa
?
yb
22
?0?y??xa
22
ba
x.
(2)若渐近线方程为y??(3)若双曲线与
2222
x?
xa
?
yb
?0?双曲线可设为
xaxax
222
?
yb
22
??.
xa
22
?
yb
22
?1有公共渐近线,可设为
?
ybyb
22
??(??0,焦点在x
轴上,??0,焦点在y轴上). (4)与双曲线(5)与双曲线
xaxa??yb
2222
222
22
?1共渐近线的双曲线系方程是?1共焦点的双曲线系方程是
?
??(??0yb
a?k
?
y
2
2
b?k
?1
(6)当a?b时?离心率e?2?两渐近线互相垂直,分别为y=?x,此时双曲线为等轴双曲线,可设为x2?y2??; 8. 双曲线的切线方程
22
22
(1)双曲线
xa
?
ybxa
?1(a?0,b?0)上一点P(x0,y0)处的切线方程是
x0xa
2
?
y0yb
2
?1.
22
(2)过双曲线是
x0xa
2
?
yb
22
?1(a?0,b?0)外一点P(x0,y0)所引两条切线的切点弦方程
?
y0yb
2
?1.
(3)双曲线
Ax?
B?y
xa
22
?
yb
22
?1(a?0,b?0)与直2
2
2
2
2
相切的条件是Aa?Bb?c0?C.
9. 直线与双曲线的位置关系
直线l:y?kx?m(m?0) 双曲线C:
?y?kx?m?2
2 ??xy
?2?2?1
b?a
xa
22
?
yb
22
?1(a>0,b>0)
(b?ak)x?2amkx?am?ab?0
ba
222222222
1) 当b2?a2k2?0,即k??曲线C相交于一点; 2) 当b2-a2k2≠0,即k
??
ba
时,直线l与双曲线的渐进线__,直线与双
时,△=(-2a2mk)2-4(b2-a2k2)(-a2k2)(-a2m2-a2b2)
① ??0时,直线l与双曲线相交,有两个公共点
② ??0时,直线l与双曲线相切,有且仅有一个公共点 ③ ??0时,直线l与双曲线相离,无公共点
3) 直线与双曲线只有一个公共点,则直线与双曲线必相切吗?为什么?(不一定)
10. 关于直线与双曲线的位置关系问题常用处理方法 直线l:y?kx?m(m?0) 双曲线C:
① 联立方程法:
?y?kx?m?2
2 ??xy
?2?2?1
b?a
xa
22
?
yb
22
?1(a>0,b>0)
(b?ak)x?2amkx?am?ab?0
222222222
设交点坐标为A(x1,y1),B(x2,y2),则有??0,以及x1?x2,x1x2,还可进一步求出
y1?y2?kx1?m?kx2?m?k(x1?x2)?2m
y1y2?(kx1?m)(kx2?m)?kx1x2?km(x1?x2)?m
2
2
,
在涉及弦长,中点,对称,面积等问题时,常用此法,比如
a. 相交弦AB的弦长
222
AB??kx1?x2??k(x1?x2)?4x1x2??k2
?a
或 AB??
1k
2
y1?y2?
1?
1k
2
(y1?y2)?4y1y2?
2
?k
2
?a
b. 中点M(x0,y0), x0?
② 点差法:
x1?x2
2
, y0?
y1?y2
2
设交点坐标为A(x1,y1),B(x2,y2),代入双曲线方程,得
x1a
2
2
?
y1b
2
2
?1
x2a
2
2
?
y2b
2
2
?1
将两式相减,可得
(x1?x2)(x1?x2)
a
2
?
(y1?y2)(y1?y2)
b
2
y1?y2x1?x2
?
b(x1?x2)a(y1?y2)
2
2
b(x1?x2)a(y1?y2)
22
a. 在涉及斜率问题时,kAB?
AB
b. 在涉及中点轨迹问题时,设线段
y1?y2x1?x2
?
b2x0a2y0
2
的中点为M(x0,y0),
2
2
?
bx0ay0
2
2
,
即kAB?
bx0ay0
2
,
btan
2
11. 焦点三角形面积公式:S?FPF
1
2
?
?
2
,(???F1PF2)。
第二篇:抛物线知识点归纳总结
抛物线知识点总结

1. 直线与抛物线的位置关系
直线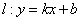 ,抛物线
,抛物线 ,
,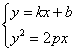 ,消y得:
,消y得: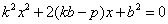
(1)当k=0时,直线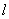 与抛物线的对称轴平行,有一个交点;
与抛物线的对称轴平行,有一个交点;
(2)当k≠0时,
Δ>0,直线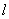 与抛物线相交,两个不同交点;
与抛物线相交,两个不同交点;
Δ=0, 直线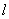 与抛物线相切,一个切点;
与抛物线相切,一个切点;
Δ<0,直线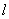 与抛物线相离,无公共点。
与抛物线相离,无公共点。
(3)若直线与抛物线只有一个公共点,则直线与抛物线必相切吗?(不一定)
2. 关于直线与抛物线的位置关系问题常用处理方法
直线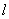 :
: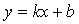 抛物线
抛物线 ,
,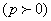
① 联立方程法:
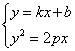
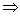
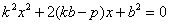
设交点坐标为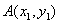 ,
,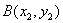 ,则有
,则有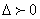 ,以及
,以及 ,还可进一步求出
,还可进一步求出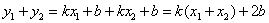 ,
,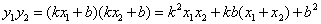
在涉及弦长,中点,对称,面积等问题时,常用此法,比如
a. 相交弦AB的弦长
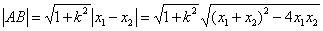
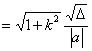
或 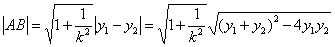
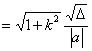
b. 中点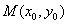 ,
, 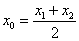 ,
, 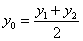
② 点差法:
设交点坐标为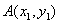 ,
,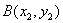 ,代入抛物线方程,得
,代入抛物线方程,得


将两式相减,可得
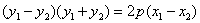
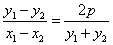

a. 在涉及斜率问题时,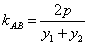
b. 在涉及中点轨迹问题时,设线段 的中点为
的中点为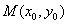 ,
,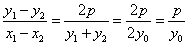 ,
,
即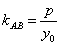 ,
,
同理,对于抛物线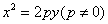 ,若直线
,若直线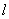 与抛物线相交于
与抛物线相交于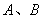 两点,点
两点,点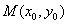 是弦
是弦 的中点,则有
的中点,则有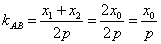
(注意能用这个公式的条件:1)直线与抛物线有两个不同的交点,2)直线的斜率存在,且不等于零)
-
双曲线知识点总结(题)
双曲线知识点总结1.双曲线的定义如果平面内一个动点到两定点距离之差的绝对值等于正的常数(小于两定点间的距离),那么动点的轨迹是双曲…
-
椭圆双曲线知识点总结
椭圆知识点在平面内到两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫椭圆.这两定点叫做椭圆的焦点,两焦点间的距离…
-
双曲线知识点总结1
双曲线知识点归纳总结1、第一定义:到两个定点F1与F2的距离之差的绝对值等于定长(<|F1F2|)的点的轨迹叫双曲线(定义表达式描…
-
双曲线知识点总结
双曲线1定义平面内与两个定点F1F2的距离之差的绝对值等于常数MF1MF22a2aF1F22c的点的轨迹称为双曲线这两个定点称为双…
-
双曲线方程知识点详细总结
双曲线方程1.双曲线的第一定义:⑴①双曲线标准方程:一般方程:⑵①i.焦点在x轴上:顶点:焦点:..准线方程.焦点:或.渐近线方程…
-
双曲线知识点总结1
双曲线知识点归纳总结1、第一定义:到两个定点F1与F2的距离之差的绝对值等于定长(<|F1F2|)的点的轨迹叫双曲线(定义表达式描…
-
椭圆双曲线知识点总结
椭圆知识点在平面内到两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫椭圆.这两定点叫做椭圆的焦点,两焦点间的距离…
-
双曲线知识点总结(题)
双曲线知识点总结1.双曲线的定义如果平面内一个动点到两定点距离之差的绝对值等于正的常数(小于两定点间的距离),那么动点的轨迹是双曲…
-
曲线运动知识点总结与经典题
曲线运动复习提纲曲线运动是高中物中的难点,由于其可综合性较强,在高考中常常与其他章节的知识综合出现。因此,在本章中,弄清各种常见模…
-
圆锥曲线知识点总结(绝对物超所值)
圆锥曲线的方程与性质1.椭圆(1)椭圆概念平面内与两个定点F1、F2的距离的和等于常数2a(大于|F1F2|)的点的轨迹叫做椭圆。…
-
圆锥曲线知识点总结
高中数学圆锥曲线选知识点总结一、椭圆1、定义:平面内与两个定点F1,F2的距离之和等于常数(大于F1F2)的点的轨迹称为椭圆.即:…