函数的周期性与函数的图象总结
函数的周期性
㈠ 主要知识:
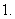 周期函数的定义:对于
周期函数的定义:对于 定义域内的每一个
定义域内的每一个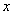 ,都存在非零常数
,都存在非零常数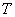 ,使得
,使得
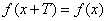 恒成立,则称函数
恒成立,则称函数 具有周期性,
具有周期性,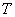 叫做
叫做 的一个周期,
的一个周期,
则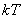 (
(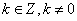 )也是
)也是 的周期,所有周期中的最小正数叫
的周期,所有周期中的最小正数叫 的最小正周期.
的最小正周期. 几种特殊的抽象函数:具有周期性的抽象函数:
几种特殊的抽象函数:具有周期性的抽象函数:
函数 满足对定义域内任一实数
满足对定义域内任一实数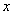 (其中
(其中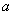 为常数),
为常数),
① 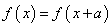 ,则
,则 是以
是以 为周期的周期函数;
为周期的周期函数;
②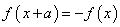 ,则
,则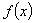 是以
是以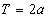 为周期的周期函数;
为周期的周期函数;
③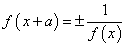 ,则
,则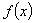 是以
是以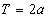 为周期的周期函数;
为周期的周期函数;
④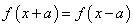 ,则
,则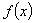 是以
是以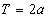 为周期的周期函数;
为周期的周期函数;
⑤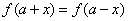 ,则
,则 是以
是以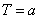 为周期的周其函数;
为周期的周其函数;
⑥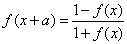 ,则
,则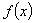 是以
是以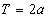 为周期的周期函数;
为周期的周期函数;
⑦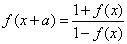 ,则
,则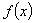 是以
是以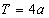 为周期的周期函数.
为周期的周期函数.
⑧函数 满足
满足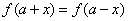 (
(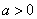 )
)
若 为奇函数,则其周期为
为奇函数,则其周期为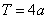 ,
,
若 为偶函数,则其周期为
为偶函数,则其周期为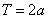 .
.
⑨函数
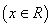 的图象关于直线
的图象关于直线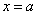 和
和
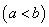 都对称,则函数
都对称,则函数 是以
是以
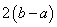 为周期的周期函数;
为周期的周期函数;
⑩函数
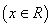 的图象关于两点
的图象关于两点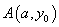 、
、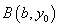
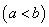 都对称,则函数
都对称,则函数 是以
是以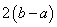 为周期的周期函数;
为周期的周期函数;
⑾函数
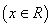 的图象关于
的图象关于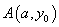 和直线
和直线
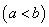 都对称,则函数
都对称,则函数 是以
是以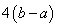 为周期的周期函数;
为周期的周期函数;
图象的对称性
一个函数的对称性:
1、函数 的图象关于点
的图象关于点 对称
对称
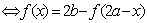
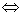

特殊的有:
① 函数 的图象关于点
的图象关于点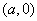 对称
对称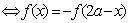 。
。
② 函数 的图象关于原点对称(奇函数)
的图象关于原点对称(奇函数)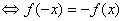 。
。
③ 函数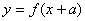 是奇函数
是奇函数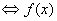 关于点
关于点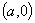 对称。
对称。
④ 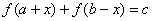 ,函数
,函数 关于点
关于点 对称
对称
2、两个函数的对称性:
① 与
与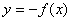 关于X轴对称。
关于X轴对称。
② 与
与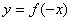 关于Y轴对称。
关于Y轴对称。
③ 与
与 关于直线
关于直线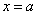 对称。
对称。
函数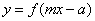 与函数
与函数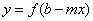 的图象关于直线
的图象关于直线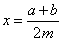 对称.
对称.
函数 与函数
与函数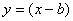 关于直线
关于直线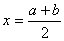 对称。
对称。
特殊地: 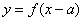 与函数
与函数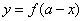 的图象关于直线
的图象关于直线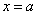 对称
对称
⑤  与
与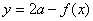 关于直线
关于直线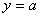 对称。
对称。
⑥ 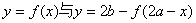 关于点(a,b)对称。
关于点(a,b)对称。
⑦  关于直线
关于直线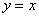 对称
对称
例1 定义在R上的非常数函数满足: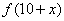 为偶函数,且
为偶函数,且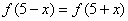 ,则
,则 一定是( )
一定是( )
A. 是偶函数,也是周期函数
B. 是偶函数,但不是周期函数
C. 是奇函数,也是周期函数
D. 是奇函数,但不是周期函数
解:因为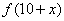 为偶函数,所以
为偶函数,所以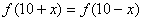 。
。
所以 有两条对称轴
有两条对称轴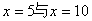 ,因此
,因此 是以10为其一个周期的周期函数,所以x=0即y轴也是
是以10为其一个周期的周期函数,所以x=0即y轴也是 的对称轴,因此
的对称轴,因此 还是一个偶函数。故选(A)。
还是一个偶函数。故选(A)。
例2 设 是定义在R上的偶函数,且
是定义在R上的偶函数,且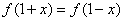 ,当
,当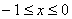 时,
时,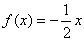 ,则
,则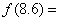 ___________
___________
解:因为f(x)是定义在R上的偶函数,所以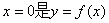 的对称轴;
的对称轴;
又因为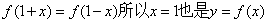 的对称轴。故
的对称轴。故 是以2为周期的周期函数,所以
是以2为周期的周期函数,所以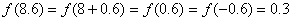
例3 函数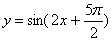 的图像的一条对称轴的方程是( )
的图像的一条对称轴的方程是( )
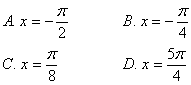
解:函数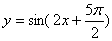 的图像的所有对称轴的方程是
的图像的所有对称轴的方程是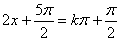 ,所以
,所以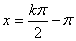 ,显然取
,显然取 时的对称轴方程是
时的对称轴方程是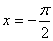 ,故选(A)。
,故选(A)。
例4 设 是定义在R上的奇函数,且
是定义在R上的奇函数,且 的图象关于直线
的图象关于直线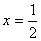 ,则:
,则: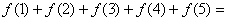 _____________
_____________
解:函数 的图像既关于原点对称,又关于直线
的图像既关于原点对称,又关于直线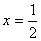 对称,所以周期是2,又
对称,所以周期是2,又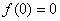 ,图像关于
,图像关于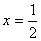 对称,所以
对称,所以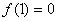 ,所以
,所以
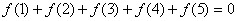
例5、函数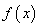 对于任意实数
对于任意实数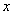 满足条件
满足条件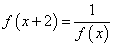 ,若
,若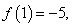 则
则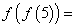 __________。
__________。
例6(08湖北卷6)已知 在R上是奇函数,且
在R上是奇函数,且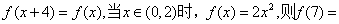 A
A
A.-2 B.2 C.-98 D.98
例7(08四川卷)函数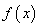 满足
满足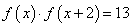 ,若
,若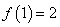 ,则
,则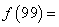 ( C )
( C )
(A)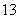 (B)
(B)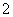 (C)
(C)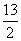 (D)
(D)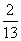
例8 (2010安徽理数)若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2则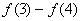 的值为( )A、
的值为( )A、 B、1 C、
B、1 C、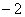 D、2
D、2
例9 (09江西卷)已知函数 是
是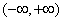 上的偶函数,若对于
上的偶函数,若对于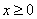 ,都有
,都有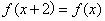 ,且当
,且当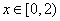 时,
时,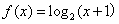 ,则
,则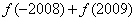 的值为 ( C )
的值为 ( C )
A.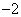 B.
B.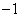 C.
C. D.
D.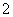
例10 2009广东三校一模)定义在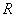 上的函数
上的函数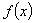 是奇函数又是以
是奇函数又是以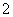 为周期的周期函数,则
为周期的周期函数,则 等于 (B)
等于 (B)
A.-1 B.0 C.1 D.4
例11 (2009全国卷Ⅰ理)函数 的定义域为R,若
的定义域为R,若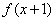 与
与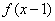 都是奇函数,
都是奇函数,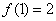 则
则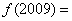 (D)
(D)
A、2009 B、-2009 C 、-2 D.、2
例12  的定义域是
的定义域是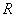 ,且
,且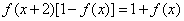 ,若
,若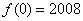
求 f(2008)的值。
解: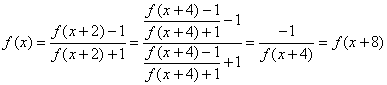
周期为8,
例13 已知函数f(x)的定义域为R,则下列命题中:
①若f(x-2)是偶函数,则函数f(x)的图象关于直线x=2对称;
②若f(x+2)=-f(x-2),则函数f(x)的图象关于原点对称;
③函数y=f(2+x)与函数y=f(2-x)的图象关于直线x=2对称;
④函数y=f(x-2)与函数y=f(2-x)的图象关于直线x=2对称.
其中正确的命题序号是 ④ .
【解析】 ①是错误的,由于f(x-2)是偶函数得f(-x-2)=f(x-2),所以f(x)的图象关于直线x=-2对称;
②是错误的,由f(x+2)=-f(x-2)得f(x+4)=-f(x),进而得f(x+8)=f(x),所以f(x)是周期为8的周期函数;
③是错误的,在第一个函数中,用-x代x,y不变,即可得第二个函数,所以这两个函数图象关于y轴对称;
④是正确的,令x-2=t,则2-x=-t,函数y=f(t)与y=f(-t)的图象关于直线t=0对称,即函数y=f(x-2)与y=f(2-x)的图象关于直线x=2对称.
例14(x)是定义在R上的以3为周期的奇函数,且f(2)=0,则方程f(x)=0在区间(0,6)内解的个数的最小值是 ( D )
A.2 B.3 C.4 D.5
【解析】 ∵f(x)为奇函数,∴f(0)=0,又函数f(x)以3为周期,且f(2)=0,∴f(-2)=0,f(1)=0,f(4)=0,f(3)=0,f(5)=0,∴在区间(0,6)内的解有1,2,3,4,5.故选D.
练习12、对函数f(x),当x∈(-∞,∞)时,f(2-x)=f(2+x),f(7-x)=f(7+x),在闭区间[0,7]上,只有f(1)=f(3)=0.
(1)试判断函数y=f(x)的奇偶性;
(2)试求方程f(x)=0在闭区间[-2005,2005]上的根的个数,并证明你的结论.
【分析】 由已知f(2+x)=f(2-x),f(7-x)=f(7+x)知f(x)的图象有两条对称轴x=2和x=7,从而知f(x)是周期为10的周期函数,又在区间[0,7]上,只有f(1)=f(3)=0,画图易知,它是非奇非偶函数,且在一个周期[0,10]上只有2个根,故易求得方程f(x)=0在的根的个数.
【解】 (1)由已知得f(0)≠0,∴f(x)不是奇函数,又由f(2-x)=f(2+x),得函数y=f(x)的对称轴为x=2,∴f(-1)=f(5)≠0,∴f(-1)≠f(1),∴f(x)不是偶函数.
故函数y=f(x)是非奇非偶函数;
(2)由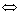
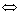 f(4-x)=f(14-x)
f(4-x)=f(14-x)  f(x)=f(x+10),
f(x)=f(x+10),
从而知y=f(x)的周期是10.
又f(3)=f(1)=0,f(11)=f(13)=f(-7)=f(-9)=0,
故f(x)在[0,10]和[-10,0]上均有两个解,从而可知函数y=f(x)在[0,2005]上有402个解,在上[-2005,0]有400个解,所以函数y=f(x)在[-2005,2005]上有802个解.
函数的图象
1.描绘函数图象的基本方法有两种:描点法与图象变换法。
2.描点法:通过 、 、 三步,画出函数的图象,有时可利用函数的性质(如奇偶性、单调性、周期性、对称性)以利于更简便的画出函数的图象。
3.函数图象变换:
.图象变换法
(1)平移变换
①水平平移:y=f(x±a)(a>0)的图象,可由y=f(x)的图象向左(+)或向右(-)平移a个单位而得到.
②竖直平移:y=f(x)±b(b>0)的图象,可由y=f(x)的图象向上(+)或向下(-)平移a个单位而得到.
(2)对称变换
①y=f(-x)与y=f(x)关于y轴对称.
②y=-f(x)与y=f(x)关于x轴对称.
③y=-f(-x)与y=f(x)关于原点对称.
④y=f-1(x)与y=f(x)关于直线y=x对称.
⑤y=|f(x)|的图象可将y=f(x)的图象在x轴下方的部分以x轴为对称轴作y=f(x)的图象的对称部分,其余部分不变.
⑥y=f(|x|)的图象可将y=f(x),x≥0的部分作出,再利用偶函数的图象关于y轴的对称性,作出x<0的图象.
(3)伸缩变换
①y=Af(x)(A>0)的图象,可将y=f(x)图象上所有点的纵坐标伸长到原来的A倍,横坐标不变而得到.
②y=f(ax)(a>0)的图象,可将y=f(x)图象上所有点的横坐标缩小原来的 倍,纵坐标不变而得到.
倍,纵坐标不变而得到.
1.作出下列函数的图象:
⑴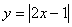 ;⑵
;⑵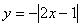 ;⑶
;⑶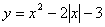 ;⑷
;⑷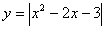 ;
;
⑸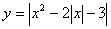 ;⑹
;⑹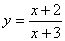 ;⑺
;⑺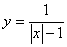 ;⑻
;⑻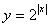 ;⑼
;⑼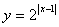 ;
;
⑽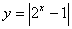 ;⑾
;⑾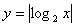 ;⑿
;⑿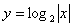 ;⒀
;⒀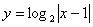 ;⒁
;⒁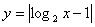 ;⒂
;⒂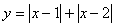
第二篇:函数周期性总结
函数的周期性
1.周期函数的定义
对于函数f(x),如果存在一个非.零.常.数.T,使得当x取定义域内的每.一.个.值.时,都有f(x?T)?f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期。 说明:(1)T必须是常数,且不为零;
(2)对周期函数来说f(x?T)?f(x)必须对定义域内的任意x都成立。
问题1 ①若常数T(≠0)为f (x)周期,问nT( n∈ N)为f (x)周期吗?为什么? ②周期函数的周期有多少个?(是有限个还是无限个)?
2 常见函数的最小正周期
正弦函数 y=sin(ωx+φ)(w>0)最小正周期为T=
y=cos(ωx+φ)(w>0)最小正周期为T= 2π2π?
y=tan(ωx+φ)(w>0)最小正周期为T= ?π
π?y=|sin(ωx+φ)|(w>0)最小正周期为T= ?
f(x)=C(C为常数)是周期函数吗?有最小正周期吗?
y=Asinw1 x+Bcosw2x 的最小正周期问题
结论:有的周期函数没有有最小正周期
3抽象函数的周期总结
1、f(x?T)?f(x) ?y?f(x)的周期为T
2、f(x?a)?f(b?x) (a?b) ?y?f(x)的周期为T?b?a 3、f(x?a)??f(x) ?y?f(x)的周期为T?2a 4、f(x?a)?c
f(x) (C为常数) ?y?f(x)的周期为T?2a 5 f(x?a)?1?f(x)
1?f(x) ?y?f(x)的周期为T?2a
7、 f(x?a)??1
f(x)?1 ?y?f(x)的周期为T?4a
8、f(x?a)?1?f(x)
1?f(x) ?y?f(x)的周期为T?4a
9、f(x?2a)?f(x?a)?f(x) ?y?f(x)的周期为T?6a
10、f(x?n?2)?f(x?n)?f(x?n?1);(它是周期函数,一个周期为6) 11、y?f(x)有两条对称轴x?a和x?b(a?b) ?y?f(x) 周期T?2(b?a) 12、y?f(x)有两个对称中心(a,0)和(b,0) ?y?f(x) 周期T?2(b?a) 13、y?f(x)有一条对称轴x?a和一个对称中心(b,0)?y?f(x) 周期T?4(b?a)
14、奇函数y?f(x)满足f(a?x)?f(a?x) ?y?f(x) 周期T?4a。
15、偶函数y?f(x)满足f(a?x)?f(a?x) ?y?f(x) 周期T?2a。 练习:①f(x+a)=-f(x) ②f(x+a)=1
f(x) ③f(x+a)=-1
f(x)
④f(x+a)=f(x)?1
f(x)?1 ⑤f(x+a)=f(x-a) T= ⑥ f(x)= f(x-a) -f(x-2a) T=6a 十一 对称性加奇偶性得到周期
f(x)为偶函数f(a+x)=f(a-x)或f(x)=f(2a-x)则T=2a f(x)为奇函数f(a+x)=f(a-x)或f(x)=f(2a-x)则T=4a eg:练1:(07天津7)在R上定义的函数f(x)是偶函数,且f(x)是减函数,则f(x)( )
A.在区间[?2,?1]上是增函数,在区间[3,4]上是减函数 B.在区间[?2,?1]上是增函数,在区间[3,4]上是减函数 C.在区间[?
2,?1]D.在区间[?
2,?1]上是减函数,在区间[3,
4]上是减函数,在区间[3,
4]?f(2?x).若f(x)在区间[1,2]上上是增函数 上是增函数
-
高中数学函数总结归纳
大成培训(函数总结归纳)一:会求函数的定义域值域。二:知道函数奇偶性的相关性质。三:会求函数的导数和用导数解决相关问题,会解含x3…
-
初中数学函数总结 形如y
初中数学函数总结形如y=kx(k为常数,且k不等于0),y就叫做x的正比例函数。图象做法:1。带定系数2。描点3。连线图象是一条直…
-
初中二次函数总结
二次函数一、函数定义与表达式1.一般式:y?ax2?bx?c(a,b,c为常数,a?0);2.顶点式:y?a(x?h)2?k(a,…
-
一元二次函数总结
一、二次函数的定义一般地,如果y=ax2+bx+c(a、b、c是常数,a≠0),那么y叫做x二次函数。注:二次函数y=ax2+bx…
-
数据库函数总结
1、将字段的值转换为汉字的函数:F_get_value(‘字段’,’’)Decode(‘’,’’,’’,’’,…)eg:f_get…
-
函数图像总结
高一数学函数图像知识点总结一、函数图像知识点汇总1.函数图象的变换1平移变换①水平平移:y=fxaa>0的图象,可由y=fx的图象…
-
高一必修四函数及其函数图像总结
诱导公式:奇变偶不变,符号看象限。①看是π/2的几倍,奇数倍变名,偶数倍不变。②符号看变之前的。③x永远当锐角。一.正弦函数:形如…
-
民办幼儿园年检总结
根据《中华人民共和国民办教育促进法》、《中华人民共和国民办教育促进法实施条例》和省、州关于对民办幼儿园进行年检的通知要求,为督促民…
-
纳家户幼儿园工会工作总结
20xx-20xx学年第二学期今年,我园工会在上级工会的正确指导下,围绕着幼儿园的总体目标,积极发挥工会作用,齐心协力,真抓实干,…
-
11号文件学习总结
20xx年x月日,新疆工程学员计算机系召集积极分子学习了自治区团委下发的由自治区下发的“11号文件”,文件总共有100个问答形式的…