三角形知识点总结
第一章 图形的初步认识
考点一、线段垂直平分线,角的平分线,垂线
1、线段垂直平分线的性质定理及逆定理
垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线。
线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
2、角的平分线及其性质
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
角的平分线有下面的性质定理:
(1)角平分线上的点到这个角的两边的距离相等。
(2)到一个角的两边距离相等的点在这个角的平分线上。
3垂线的性质:
性质1:过一点有且只有一条直线与已知直线垂直。
性质2:直线外一点与直线上各点连接的所有线段中,垂线段最短。简称:垂线段最短。
考点二、平行线
1、平行线的概念
在同一个平面内,不相交的两条直线叫做平行线。同一平面内,两条直线的位置关系只有两种:相交或平行。
4、平行线的性质
(1)两直线平行,同位角相等;(2)两直线平行,内错角相等;(3)两直线平行,同旁内角互补。
考点三、投影与视图
1、投影
投影的定义:用光线照射物体,在地面上或墙壁上得到的影子,叫做物体的投影。
平行投影:由平行光线(如太阳光线)形成的投影称为平行投影。
中心投影:由同一点发出的光线所形成的投影称为中心投影。
2、视图
当我们从某一角度观察一个实物时,所看到的图像叫做物体的一个视图。物体的三视图特指主视图、俯视图、左视图。
主视图:在正面内得到的由前向后观察物体的视图,叫做主视图。
俯视图:在水平面内得到的由上向下观察物体的视图,叫做俯视图。
左视图:在侧面内得到的由左向右观察物体的视图,叫做左视图,有时也叫做侧视图。
第二章 三角形
1、三角形的概念
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。组成三角形的线段叫做三角形的边;相邻两边的公共端点叫做三角形的顶点;相邻两边所组成的角叫做三角形的内角,简称三角形的角。
2、三角形中的主要线段
(1)三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线。
(2)在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线。
(3)从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高)。
3、三角形的稳定性
三角形的形状是固定的,三角形的这个性质叫做三角形的稳定性。三角形的这个性质在生产生活中应用很广,需要稳定的东西一般都制成三角形的形状。
4、三角形的特性与表示
三角形有下面三个特性:
 (1)三角形有三条线段
(1)三角形有三条线段
(2)三条线段不在同一直线上 三角形是封闭图形
(3)首尾顺次相接
三角形用符号“ ”表示,顶点是A、B、C的三角形记作“
”表示,顶点是A、B、C的三角形记作“ ABC”,读作“三角形ABC”。
ABC”,读作“三角形ABC”。
5、三角形的分类
三角形按边的关系分类如下:
 不等边三角形
不等边三角形
 三角形 底和腰不相等的等腰三角形
三角形 底和腰不相等的等腰三角形
等腰三角形
等边三角形
三角形按角的关系分类如下:
 直角三角形(有一个角为直角的三角形)
直角三角形(有一个角为直角的三角形)
 三角形 锐角三角形(三个角都是锐角的三角形)
三角形 锐角三角形(三个角都是锐角的三角形)
斜三角形
钝角三角形(有一个角为钝角的三角形)
把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。
6、三角形的三边关系定理及推论
(1)三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
(2)三角形三边关系定理及推论的作用:
①判断三条已知线段能否组成三角形
②当已知两边时,可确定第三边的范围。
③证明线段不等关系。
7、三角形的角关系
三角形的内角和定理:三角形三个内角和等于180°。
推论:
①直角三角形的两个锐角互余。
②三角形的一个外角等于和它不相邻的来两个内角的和。
③三角形的一个外角大于任何一个和它不相邻的内角。
注:在同一个三角形中:等角对等边;等边对等角;大角对大边;大边对大角。等角的补角相等,等角的余角相等。
8、三角形的面积
三角形的面积=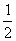 ×底×高
×底×高
应用:经常利用两个三角形面积关系求底、高的比例关系或值
考点二、全等三角形
1、全等三角形的概念
能够完全重合的两个三角形叫做全等三角形。
能够完全重合的两个三角形叫做全等三角形。两个三角形全等时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角。夹边就是三角形中相邻两角的公共边,夹角就是三角形中有公共端点的两边所成的角。
2、三角形全等的判定
三角形全等的判定定理:
(1)边角边定理:有两边和它们的夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS”)
(2)角边角定理:有两角和它们的夹边对应相等的两个三角形全等(可简写成“角边角”或“ASA”)
(3)边边边定理:有三边对应相等的两个三角形全等(可简写成“边边边”或“SSS”)。
直角三角形全等的判定:
对于特殊的直角三角形,判定它们全等时,还有HL定理(斜边、直角边定理):有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”)
3、全等变换
只改变图形的位置,不改变其形状大小的图形变换叫做全等变换。
全等变换包括一下三种:
(1)平移变换:把图形沿某条直线平行移动的变换叫做平移变换。
(2)对称变换:将图形沿某直线翻折180°,这种变换叫做对称变换。
(3)旋转变换:将图形绕某点旋转一定的角度到另一个位置,这种变换叫做旋转变换。
考点三、等腰三角形
1、等腰三角形的性质
(1)等腰三角形的性质定理及推论:
定理:等腰三角形的两个底角相等(简称:等边对等角)
推论1:等腰三角形顶角平分线平分底边并且垂直于底边。即等腰三角形的顶角平分线、底边上的中线、底边上的高重合。
推论2:等边三角形的各个角都相等,并且每个角都等于60°。
(2)等腰三角形的其他性质:
①等腰直角三角形的两个底角相等且等于45°
②等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角)。
③等腰三角形的三边关系:设腰长为a,底边长为b,则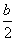 <a
<a
④等腰三角形的三角关系:设顶角为顶角为∠A,底角为∠B、∠C,则∠A=180°—2∠B,∠B=∠C=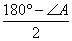
2、等腰三角形的判定
等腰三角形的判定定理及推论:
定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边)。这个判定定理常用于证明同一个三角形中的边相等。
推论1:三个角都相等的三角形是等边三角形
推论2:有一个角是60°的等腰三角形是等边三角形。
推论3:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
3、三角形中的中位线
连接三角形两边中点的线段叫做三角形的中位线。
(1)三角形共有三条中位线,并且它们又重新构成一个新的三角形。
(2)要会区别三角形中线与中位线。
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
三角形中位线定理的作用:
位置关系:可以证明两条直线平行。
数量关系:可以证明线段的倍分关系。
常用结论:任一个三角形都有三条中位线,由此有:
结论1:三条中位线组成一个三角形,其周长为原三角形周长的一半。
结论2:三条中位线将原三角形分割成四个全等的三角形。
结论3:三条中位线将原三角形划分出三个面积相等的平行四边形。
结论4:三角形一条中线和与它相交的中位线互相平分。
结论5:三角形中任意两条中位线的夹角与这夹角所对的三角形的顶角相等。
第三章 解直角三角形
考点一、直角三角形的性质
1、直角三角形的两个锐角互余
2、在直角三角形中,30°角所对的直角边等于斜边的一半。
3、直角三角形斜边上的中线等于斜边的一半
4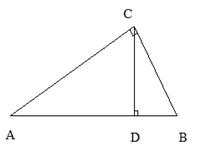 直角三角形两直角边a,b的平方和等于斜边c的平方,即
直角三角形两直角边a,b的平方和等于斜边c的平方,即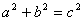
5、摄影定理
在直角三角形中,斜边上的高线是两直角边在斜边上的摄影的比例中项,每条直角边是它们在斜边上的摄影和斜边的比例中项
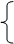
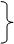 ∠ACB=90°
∠ACB=90° 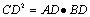
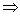
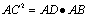
CD⊥AB 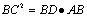
6、常用关系式
由三角形面积公式可得:
AB CD=AC
CD=AC BC
BC
考点二、锐角三角函数的概念 (3~8分)
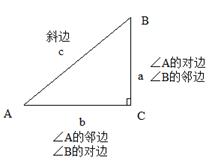 1、如图,在△ABC中,∠C=90°
1、如图,在△ABC中,∠C=90°
①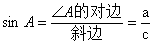
②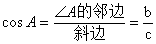
③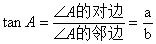
④
2、一些特殊角的三角函数值
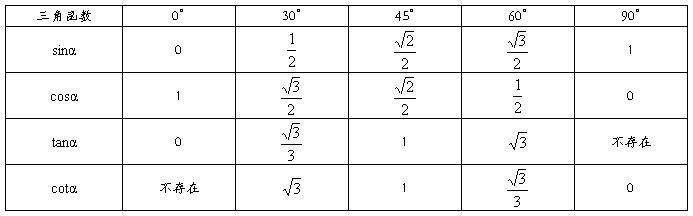
3、各锐角三角函数之间的关系
(1)互余关系:sinA=cos(90°—A),cosA=sin(90°—A),tanA=cot(90°—A),cotA=tan(90°—A)
(2)平方关系: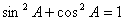
(3)倒数关系:tanA tan(90°—A)=1
tan(90°—A)=1
(4)弦切关系:tanA=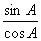
第四章 图形的相似
考点一、比例线段
1、比例的性质
(1)基本性质
①a:b=c:d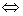 ad=bc
ad=bc
②a:b=b:c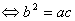
(2)更比性质(交换比例的内项或外项)
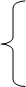
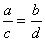 (交换内项)
(交换内项)
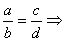
 (交换外项)
(交换外项)
 (同时交换内项和外项)
(同时交换内项和外项)
(3)反比性质(交换比的前项、后项):

(4)合比性质:
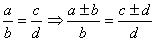
(5)等比性质:
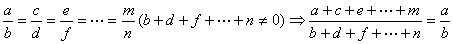
3、黄金分割
把线段AB分成两条线段AC,BC(AC>BC),并且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=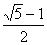 AB
AB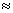 0.618AB
0.618AB
考点二、平行线分线段成比例定理
三条平行线截两条直线,所得的对应线段成比例。
考点三、相似三角形
1、相似三角形的概念
对应角相等,对应边成比例的三角形叫做相似三角形。相似用符号“∽”来表示
2、相似三角形的基本定理
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。

相似三角形的等价关系:
(1)反身性:对于任一△ABC,都有△ABC∽△ABC;
(2)对称性:若△ABC∽△A’B’C’,则△A’B’C’∽△ABC
(3)传递性:若△ABC∽△A’B’C’,并且△A’B’C’∽△A’’B’’C’’,则△ABC∽△A’’B’’C’’。
3、三角形相似的判定
(1)三角形相似的判定方法
①定义法:对应角相等,对应边成比例的两个三角形相似
②平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似
③判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,可简述为两角对应相等,两三角形相似。
④判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似,可简述为两边对应成比例且夹角相等,两三角形相似。
⑤判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简述为三边对应成比例,两三角形相似
(2)直角三角形相似的判定方法
①以上各种判定方法均适用
②定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似
4、相似三角形的性质
(1)相似三角形的对应角相等,对应边成比例
(2)相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比
(3)相似三角形周长的比等于相似比
(4)相似三角形面积的比等于相似比的平方。
5、相似多边形
(1)如果两个边数相同的多边形的对应角相等,对应边成比例,那么这两个多边形叫做相似多边形。相似多边形对应边的比叫做相似比(或相似系数)
(2)相似多边形的性质
①相似多边形的对应角相等,对应边成比例
②相似多边形周长的比、对应对角线的比都等于相似比
③相似多边形中的对应三角形相似,相似比等于相似多边形的相似比
④相似多边形面积的比等于相似比的平方
6、位似图形
如果两个图形不仅是相似图形,而且每组对应点所在直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,此时的相似比叫做位似比。
性质:每一组对应点和位似中心在同一直线上,它们到位似中心的距离之比都等于位似比。
由一个图形得到它的位似图形的变换叫做位似变换。利用位似变换可以把一个图形放大或缩小。
第五章 三角形的五心
三角形中有许多重要的特殊点,特别是三角形的“五心”,在解题时有很多应用,在本节中将分别给予介绍.
 三角形的“五心”指的是三角形的外心,内心,重心,垂心和旁心.
三角形的“五心”指的是三角形的外心,内心,重心,垂心和旁心.
1、三角形的外心
三角形的三条边的垂直平分线交于一点,这点称为三角形的外心(外接圆圆心).
三角形的外心到三角形的三个顶点距离相等. 都等于三角形的外接圆半径.
锐角三角形的外心在三角形内;直角三角形的外心在斜边中点;
 钝角三角形的外心在三角形外.
钝角三角形的外心在三角形外.
2、三角形的内心
三角形的三条内角平分线交于一点,这点称为三角形的内心(内切圆圆心).
三角形的内心到三边的距离相等,都等于三角形内切圆半径.
内切圆半径r的计算:
 设三角形面积为S,并记p=(a+b+c),则r=.
设三角形面积为S,并记p=(a+b+c),则r=.
特别的,在直角三角形中,有 r=(a+b-c).
3、三角形的重心
三角形的三条中线交于一点,这点称为三角形的重心.
 上面的证明中,我们也得到了以下结论:三角形的重心到边的中点与到相应顶点的距离之比为 1∶ 2.
上面的证明中,我们也得到了以下结论:三角形的重心到边的中点与到相应顶点的距离之比为 1∶ 2.
4、三角形的垂心
三角形的三条高交于一点,这点称为三角形的垂心.
斜三角形的三个顶点与垂心这四个点中,任何三个为顶点的三角形的垂心就是第四个点.所以把这样的四个点称为一个“垂心组”.
5、三角形的旁心
三角形的一条内角平分线与另两个外角平分线交于一点,称为三角形的旁心(旁切 圆圆心).每个三角形都有三个旁切圆.
圆圆心).每个三角形都有三个旁切圆.
A类例题
例1 证明重心定理。
证法1 如图,D、E、F为三边中点,设BE、CF交于G,连接EF,显然EF ∥=BC,由三角形相似可得GB=2GE,GC=2GF.
又设AD、BE交于G',同理可证G'B=2G'E,G'A=2G'D,即G、G'都是BE上从B到E的三分之二处的点,故G'、G重合.
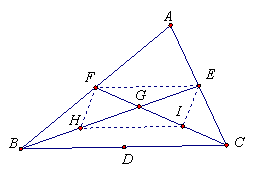 即三条中线AD、BE、CF相交于一点G.
即三条中线AD、BE、CF相交于一点G.
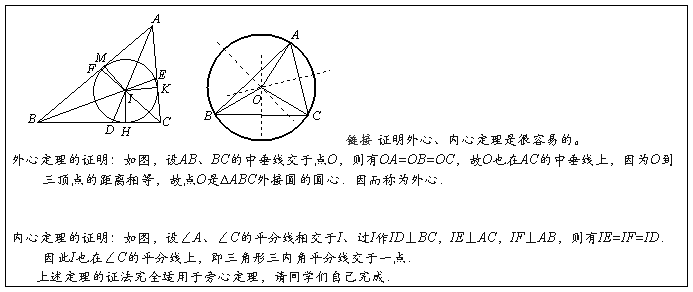
证法2 设BE、CF交于G,BG、CG中点为H、I.连EF、FH、HI、IE,
因为EF ∥=BC,HI ∥=BC,
所以 EFHI为平行四边形.
所以 HG=GE、IG=GF,GB=2GE,GC=2GF.
同证法1可知AG=2GD,AD、BE、CF共点.
即定理证毕.
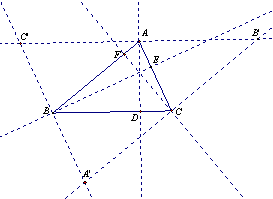
例2证明垂心定理
分析 我们可以利用构造外心来进行证明。
证明 如图,AD、BE、CF为ΔABC三条高,过点A、B、C分别作对边的平行线相交成ΔA'B'C',显然AD为B'C'的中垂线;同理BE、CF也分别为A'C'、A'B'的中垂线,由外心定理,它们交于一点,命题得证.

 情景再现
情景再现
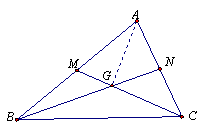
1.设G为△ABC的重心,M、N分别为AB、CA的中点,求证:四边形GMAN和△GBC的面积相等.
2.三角形的任一顶点到垂心的距离,等于外心到对边的距离的二倍.
B类例题
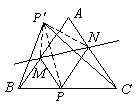 例3 过等腰△ABC底边BC上一点P引PM∥CA交AB于M;引PN∥BA交AC于N.
例3 过等腰△ABC底边BC上一点P引PM∥CA交AB于M;引PN∥BA交AC于N.
作点P关于MN的对称点P'.试证:P'点在△ABC外接圆上.(杭州大学《中学数学竞赛习题》)
分析 分析点M和N的性质,即能得到解题思路。
证明 由已知可得MP'=MP=MB,NP'=NP=NC,
故点M是△P'BP的外心,点N是△P'PC的外心.于是有
∠BP'P=∠BMP=∠BAC,
∠PP'C=∠PNC=∠BAC.
∴∠BP'C=∠BP'P+∠P'PC=∠BAC.
从而,P'点与A、B、C共圆,即P'在△ABC外接圆上.
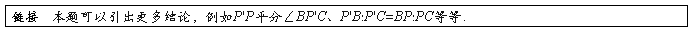
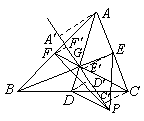 例4 AD,BE,CF是△ABC的三条中线,P是任意一点.
例4 AD,BE,CF是△ABC的三条中线,P是任意一点.
证明:在△PAD,△PBE,△PCF中,其中一个面积等于另外两个面积的和. (第26届莫斯科数学奥林匹克)
证明 设G为△ABC重心,直线PG与AB,BC相交.从A,C,D,E,F分别作该直线的垂线,垂足为A',C',D',E',F'.
易证AA'=2DD',CC'=2FF',2EE'=AA'+CC',
∴EE'=DD'+FF'.
有S△PGE=S△PGD+S△PGF.
两边各扩大3倍,有S△PBE=S△PAD+S△PCF.
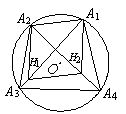
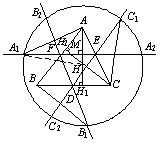
例5 设A1A2A3A4为⊙O内接四边形,H1,H2,H3,H4依次为△A2A3A4,△A3A4A1,△A4A1A2,△A1A2A3的垂心.求证:H1,H2,H3,H4四点共圆,并确定出该圆的圆心位置. (1992,全国高中联赛)
证明 连接A2H1,A1H2,H1H2,记圆半径为R.由△A2A3A4知
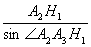 =2R
=2R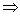 A2H1=2Rcos∠A3A2A4;
A2H1=2Rcos∠A3A2A4;
由△A1A3A4得 A1H2=2Rcos∠A3A1A4.
但∠A3A2A4=∠A3A1A4,故A2H1=A1H2.
易证A2H1∥A1A2,于是,A2H1 ∥=A1H2,
故得H1H2 ∥=A2A1.设H1A1与H2A2的交点为M,故H1H2与A1A2关于M点成中心对称.
同理,H2H3与A2A3,H3H4与A3A4,H4H1与A4A1都关于M点成中心对称.故四边形H1H2H3H4与四边形A1A2A3A4关于M点成中心对称,两者是全等四边形,H1,H2,H3,H4在同一个圆上.后者的圆心设为Q,Q与O也关于M成中心对称.由O,M两点,Q点就不难确定了.

情景再现
3.在△ABC的边AB,BC,CA上分别取点P,Q,S.
证明以△APS,△BQP,△CSQ的外心为顶点的三角形与△ABC相似.
(B·波拉索洛夫《中学数学奥林匹克》)
4.如果三角形三边的平方成等差数列,那么该三角形和由它的三条中线围成的新三角形相似.其逆亦真.
C类例题
例6 H为△ABC的垂心,D,E,F分别是BC,CA,AB的中心.一个以H为圆心的⊙H交直线EF,FD,DE于A1,A2,B1,B2,C1,C2.
求证:AA1=AA2=BB1=BB2=CC1=CC2. (1989,加拿大数学奥林匹克训练题)
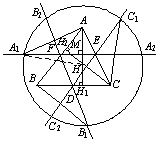 分析 只须证明AA1=BB1=CC1即可.
分析 只须证明AA1=BB1=CC1即可.
证明 设BC=a, CA=b,AB=c,△ABC外接圆半径为R,⊙H的半径为r.
连HA1,AH交EF于M. A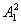 =AM2+A1M2=AM2+r2-MH2
=AM2+A1M2=AM2+r2-MH2
=r2+(AM2-MH2), ①
又AM2-HM2=(AH1)2-(AH-AH1)2
=AH·AH1-AH2=AH2·AB-AH2
=cosA·bc-AH2, ②
而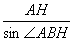 =2R
=2R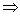 AH2=4R2cos2A,
AH2=4R2cos2A,
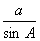 =2R
=2R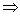 a2=4R2sin2A.
a2=4R2sin2A.
∴AH2+a2=4R2,AH2=4R2-a2. ③
由①、②、③有
A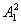 =r2+
=r2+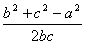 ·bc-(4R2-a2)
·bc-(4R2-a2)
= (a2+b2+c2)-4R2+r2.
同理,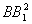 =
=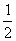 (a2+b2+c2)-4R2+r2,
(a2+b2+c2)-4R2+r2,
 = (a2+b2+c2)-4R2+r2.
= (a2+b2+c2)-4R2+r2.
故有AA1=BB1=CC1.
例7 已知⊙O内接△ABC,⊙Q切AB,AC于E,F且与⊙O内切.试证:EF中点P是△ABC之内心.(B·波拉索洛夫《中学数学奥林匹克》)
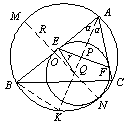 证明 如图,显然EF中点P、圆心Q,︵BC中点K都在∠BAC平分线上.易知AQ=
证明 如图,显然EF中点P、圆心Q,︵BC中点K都在∠BAC平分线上.易知AQ=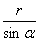 .
.
∵QK·AQ=MQ·QN,
∴QK=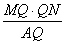
=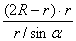 =
= .
.
由Rt△EPQ知PQ=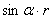 .
.
∴PK=PQ+QK=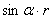 +
+ =
=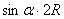 .
.
∴PK=BK.
利用内心等量关系之逆定理,即知P是△ABC这内心.
说明 在第20届IMO中,美国提供的一道题实际上是例7的一种特例,但它增加了条件AB=AC.
例8 在直角三角形中,求证:r+ra+rb+rc=2p.式中r,ra,rb,rc分别表示内切圆半径及与a,b,c相切的旁切圆半径,p表示半周. (杭州大学《中学数学竞赛习题》)
证明 设Rt△ABC中,c为斜边,先来证明一个特性:
p(p-c)=(p-a)(p-b).
 ∵p(p-c)= (a+b+c)·(a+b-c)
∵p(p-c)= (a+b+c)·(a+b-c)
=[(a+b)2-c2]
=ab;
(p-a)(p-b)= (-a+b+c)·(a-b+c)
=[c2-(a-b)2]= ab.
∴p(p-c)=(p-a)(p-b). ①
观察图形,可得
ra=AF-AC=p-b,
rb=BG-BC=p-a,
rc=CK=p.
而r=(a+b-c)=p-c.
∴r+ra+rb+rc =(p-c)+(p-b)+(p-a)+p
=4p-(a+b+c)=2p.
由①及图形易证.
例9 M是△ABC边AB上的任意一点.r1,r2,r分别是△AMC,△BMC,△ABC内切圆的半径,q1,q2,q分别是上述三角形在∠ACB内部的旁切圆半径.证明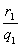 ·
·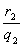 =
= .(IMO-12)
.(IMO-12)
证明 对任意△A'B'C',由正弦定理可知
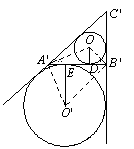 OD=OA'·
OD=OA'·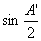
=A'B'·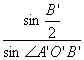 ·
·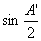
=A'B'·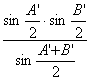 ,
,
O'E= A'B'·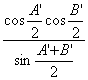 .
.
∴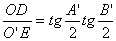 .
.
亦即有
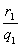 ·
·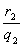 =
=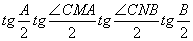
=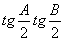 =
= .
.
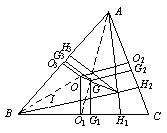 例10 锐角△ABC中,O,G,H分别是外心、重心、垂心.设外心到三边距离和为d外,重心到三边距离和为d重,垂心到三边距离和为d垂.
例10 锐角△ABC中,O,G,H分别是外心、重心、垂心.设外心到三边距离和为d外,重心到三边距离和为d重,垂心到三边距离和为d垂.
求证:1·d垂+2·d外=3·d重.
证明 设△ABC外接圆半径为1,三个内角记为A,B,
C. 易知d外=OO1+OO2+OO3
=cosA+cosB+cosC,
∴2d外=2(cosA+cosB+cosC). ①
∵AH1=sinB·AB=sinB·(2sinC)=2sinB·sinC,
同样可得BH2·CH3.
∴3d重=△ABC三条高的和
=2·(sinB·sinC+sinC·sinA+sinA·sinB) ②
∴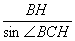 =2,
=2,
∴HH1=cosC·BH=2·cosB·cosC.
同样可得HH2,HH3.
∴d垂=HH1+HH2+HH3
=2(cosB·cosC+cosC·cosA+cosA·cosB) ③
欲证结论,观察①、②、③,
须证(cosB·cosC+cosC·cosA+cosA·cosB)+( cosA+ cosB+ cosC)=sinB·sinC+sinC·sinA+sinA·sinB.即可.
说明 本题用了三角法。
情景再现
5.设在圆内接凸六边形ABCDFE中,AB=BC,CD=DE,EF=FA.试证:(1)AD,BE,CF三条对角线交于一点;(2)AB+BC+CD+DE+EF+FA≥AK+BE+CF.
(1991,国家教委数学试验班招生试题)
6.△ABC的外心为O,AB=AC,D是AB中点,E是△ACD的重心.证明OE丄CD.
(加拿大数学奥林匹克训练题)
7.△ABC中∠C=30°,O是外心,I是内心,边AC上的D点与边BC上的E点使得AD=BE=AB.求证:OI丄DE,OI=DE. (1988,中国数学奥林匹克集训题)
习题17
1.在△ABC中,∠A是钝角,H是垂心,且AH=BC,则cos∠BHC=( )
A.- B. C. D.
2.如果一个三角形的面积与周长都被一条直线平分,则此直线一定通过三角形的( )
A.内心 B.外心 C.重心 D.垂心(1996年全国初中联赛)
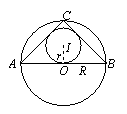 3.(1997年安徽省初中数学竞赛)若0°<a<90°,那么,以sina,cosa,tanacota为三边的三角形有内切圆、外接圆的半径之和是( )
3.(1997年安徽省初中数学竞赛)若0°<a<90°,那么,以sina,cosa,tanacota为三边的三角形有内切圆、外接圆的半径之和是( )
A. B. C.2sinacosa D.
4.ΔABC中,∠A=45°,BC=a,高BE、CF交于点H,则AH=( )
A.a B.a C.a D.a
5.下面三个命题中:
⑴ 设H为ΔABC的高AD上一点,∠BHC+∠BAC=180°,则点H是ΔABC的垂心;
 ⑵ 设G为ΔABC的中线AD上一点,且SΔAGB=SΔBGC,则点G是ΔABC的重心;
⑵ 设G为ΔABC的中线AD上一点,且SΔAGB=SΔBGC,则点G是ΔABC的重心;
⑶ 设E是ΔABC的外角∠BAK的角平分线与ΔABC的外接圆⊙O的交点,ED是⊙O的直径,I在线段AD上,且DI=DB,则I是ΔABC的内心.
正确命题的个数是( )
A.0个 B.1个 C.2个 D.3个
6.设ΔABC的∠A=60°,求证:ΔABC的外心O、内心I、垂心H及点B、C五点在同一个圆上.
 7.已知P是□ABCD内的一点,O为AC与BD的交点,M、N分别为PB、PC中点,Q为AN与DM的交点.求证:
7.已知P是□ABCD内的一点,O为AC与BD的交点,M、N分别为PB、PC中点,Q为AN与DM的交点.求证:
⑴ P、Q、O三点在一条直线上;
⑵ PQ=2OQ.
8.I为△ABC之内心,射线AI,BI,CI交△ABC外接圆于A′,
B′,C ′.则AA′+BB′+CC′>△ABC周长.(1982,澳大利亚数学奥林匹克)
9.△T′的三边分别等于△T的三条中线,且两个三角形有一组角相等.求证这两个三角形相似.(1989,捷克数学奥林匹克)
10.I为△ABC的内心.取△IBC,△ICA,△IAB的外心O1,O2,O3.求证:△O1O2O3与△ABC有公共的外心.(1988,美国数学奥林匹克)
11.AD为△ABC内角平分线.取△ABC,△ABD,△ADC的外心O,O1,O2.则△OO1O2是等腰三角形.
12.△ABC中∠C<90°,从AB上M点作CA,CB的垂线MP,MQ.H是△CPQ的垂心.当M是AB上动点时,求H的轨迹.(IMO-7)
本节“情景再现”解答
 1.证明 如图,连GA,因为M、N分别为AB、CA的中点,所以△AMG的面积=△GBM的面积,△GAN的面积=△GNC的面积,
1.证明 如图,连GA,因为M、N分别为AB、CA的中点,所以△AMG的面积=△GBM的面积,△GAN的面积=△GNC的面积,
即四边形GMAN和△GBC的面积相等.
 2.证明 如图,O为ΔABC的外心,H为垂心,连CO交ΔABC外接圆于D,连DA、DB,则DA⊥AC,BD⊥BC,又AH⊥BC,BH⊥AC.所以DA∥BH,BD∥AH,从而四边形DAHB为平行四边形。又显然DB=2OM,所以AH=2OM.
2.证明 如图,O为ΔABC的外心,H为垂心,连CO交ΔABC外接圆于D,连DA、DB,则DA⊥AC,BD⊥BC,又AH⊥BC,BH⊥AC.所以DA∥BH,BD∥AH,从而四边形DAHB为平行四边形。又显然DB=2OM,所以AH=2OM.
同理可证 BH=2ON,CH=2OK.证毕.
3.提示:设O1,O2,O3是△APS,△BQP,△CSQ的外心,作出六边形O1PO2QO3S后再由外心性质可知∠PO1S=2∠A,∠QO2P=2∠B,∠SO3Q=2∠C.
∴∠PO1S+∠QO2P+∠SO3Q=360°.从而又知∠O1PO2+∠O2QO3+∠O3SO1=360°
将△O2QO3绕着O3点旋转到△KSO3,易判断△KSO1≌△O2PO1,
同时可得△O1O2O3≌△O1KO3.∴∠O2O1O3=∠KO1O3=∠O2O1K
= (∠O2O1S+∠SO1K)= (∠O2O1S+∠PO1O2)= ∠PO1S=∠A;
同理有∠O1O2O3=∠B.故△O1O2O3∽△ABC.
4.提示:将△ABC简记为△,由三中线AD,BE,CF围成的三角形简记为△'.G为重心,连DE到H,使EH=DE,连HC,HF,则△'就是△HCF. (1)a2,b2,c2成等差数列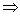 △∽△'.若△ABC为正三角形,易证△∽△'.不妨设a≥b≥c,有
△∽△'.若△ABC为正三角形,易证△∽△'.不妨设a≥b≥c,有
CF=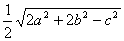 ,BE=
,BE= ,AD=
,AD=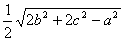 .
.
将a2+c2=2b2,分别代入以上三式,得CF= ,BE=
,BE=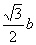 ,AD=
,AD=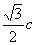 .
.
∴CF:BE:AD = :
: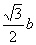 :
: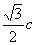 =a:b:c. 故有△∽△′.
=a:b:c. 故有△∽△′.
(2)△∽△′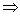 a2,b2,c2成等差数列.当△中a≥b≥c时,
a2,b2,c2成等差数列.当△中a≥b≥c时,
△′中CF≥BE≥AD.∵△∽△′,∴ =(
=(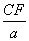 )2.
)2.
据“三角形的三条中线围成的新三角形面积等于原三角形面积的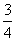 ”,有
”,有 =
=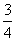 .
.
∴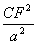 =
=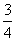
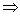 3a2=4CF2=2a2+b2-c2
3a2=4CF2=2a2+b2-c2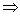 a2+c2=2b2.
a2+c2=2b2.
5.证明 连接AC,CE,EA,由已知可证AD,CF,EB是△ACE的三条内角平分线,I为△ACE的内心.从而有ID=CD=DE,IF=EF=FA,IB=AB=BC.
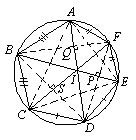 再由△BDF,易证BP,DQ,FS是它的三条高,I是它的垂心,利用 不等式有:
再由△BDF,易证BP,DQ,FS是它的三条高,I是它的垂心,利用 不等式有:
BI+DI+FI≥2·(IP+IQ+IS). 不难证明IE=2IP,IA=2IQ,IC=2IS.
∴BI+DI+FI≥IA+IE+IC. ∴AB+BC+CD+DE+EF+FA=2(BI+DI+FI)
≥(IA+IE+IC)+(BI+DI+FI)=AD+BE+CF.
I就是一点两心.
6.提示:设AM为高亦为中线,取AC中点
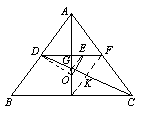 F,E必在DF上且DE:EF=2:1.设
F,E必在DF上且DE:EF=2:1.设
CD交AM于G,G必为△ABC重心.
连GE,MF,MF交DC于K.易证:
DG:GK=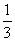 DC:(
DC:(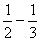 )DC=2:1.
)DC=2:1.
∴DG:GK=DE:EF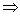 GE∥MF.
GE∥MF.
∵OD丄AB,MF∥AB,
∴OD丄MF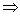 OD丄GE.但OG丄DE
OD丄GE.但OG丄DE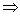 G又是△ODE之垂心.
G又是△ODE之垂心.
易证OE丄CD.
 7.提示:辅助线如图所示,作∠DAO平分线交BC于K.
7.提示:辅助线如图所示,作∠DAO平分线交BC于K.
易证△AID≌△AIB≌△EIB,
∠AID=∠AIB=∠EIB.
利用内心张角公式,有
∠AIB=90°+∠C=105°,
∴∠DIE=360°-105°×3=45°. ∵∠AKB=30°+∠DAO=30°+ (∠BAC-∠BAO)=30°+ (∠BAC-60°)=∠BAC=∠BAI=∠BEI.
∴AK∥IE. 由等腰△AOD可知DO丄AK,∴DO丄IE,即DF是△DIE的一条高.
同理EO是△DIE之垂心,OI丄DE.由∠DIE=∠IDO,易知OI=DE.
习题17解答
1. B;2.A;3.A;4.C;5.选B,只有(3)是对的;
6.略;7.略;8.略;9.略;10.略;11.略;12. H的轨迹是一条线段.
补充:
第五讲 三角形的五心
三角形的外心、重心、垂心、内心及旁心,统称为三角形的五心.
一、外心.
三角形外接圆的圆心,简称外心.与外心关系密切的有圆心角定理和圆周角定理.
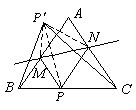
例1.过等腰△ABC底边BC上一点P引PM∥CA交AB于M;引PN∥BA交AC于N.作点P关于MN的对称点P′.试证:P′点在△ABC外接圆上.
 (杭州大学《中学数学竞赛习题》)
(杭州大学《中学数学竞赛习题》)
分析:由已知可得MP′=MP=MB,NP′=NP
=NC,故点M是△P′BP的外心,点
N是△P′PC的外心.有
∠BP′P=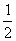 ∠BMP=
∠BMP=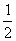 ∠BAC,
∠BAC,
∠PP′C=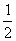 ∠PNC=
∠PNC=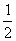 ∠BAC.
∠BAC.
∴∠BP′C=∠BP′P+∠P′PC=∠BAC.
从而,P′点与A,B,C共圆、即P′在△ABC外接圆上.
由于P′P平分∠BP′C,显然还有
P′B:P′C=BP:PC.
例2.在△ABC的边AB,BC,CA上分别取点P,Q,S.证明以△APS,△BQP,△CSQ的外心为顶点的三角形与△ABC相似.
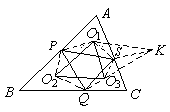 (B·波拉索洛夫《中学数学奥林匹克》)
(B·波拉索洛夫《中学数学奥林匹克》)
分析:设O1,O2,O3是△APS,△BQP,
△CSQ的外心,作出六边形
O1PO2QO3S后再由外
心性质可知
∠PO1S=2∠A,
∠QO2P=2∠B,
∠SO3Q=2∠C.
∴∠PO1S+∠QO2P+∠SO3Q=360°.从而又知∠O1PO2+
∠O2QO3+∠O3SO1=360°
将△O2QO3绕着O3点旋转到△KSO3,易判断△KSO1≌△O2PO1,同时可得△O1O2O3≌△O1KO3.
∴∠O2O1O3=∠KO1O3=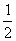 ∠O2O1K
∠O2O1K
=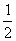 (∠O2O1S+∠SO1K)
(∠O2O1S+∠SO1K)
=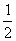 (∠O2O1S+∠PO1O2)
(∠O2O1S+∠PO1O2)
=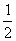 ∠PO1S=∠A;
∠PO1S=∠A;
同理有∠O1O2O3=∠B.故△O1O2O3∽△ABC.
二、重心
三角形三条中线的交点,叫做三角形的重心.掌握重心将每
条中线都分成定比2:1及中线长度公式,便于解题.
 例3.AD,BE,CF是△ABC的三条中线,P是任意一点.证明:在△PAD,△PBE,△PCF中,其中一个面积等于另外两个面积的和.
例3.AD,BE,CF是△ABC的三条中线,P是任意一点.证明:在△PAD,△PBE,△PCF中,其中一个面积等于另外两个面积的和.
(第26届莫斯科数学奥林匹克)
分析:设G为△ABC重心,直线PG与AB
,BC相交.从A,C,D,E,F分别
作该直线的垂线,垂足为A′,C′,
D′,E′,F′.
易证AA′=2DD′,CC′=2FF′,2EE′=AA′+CC′,
∴EE′=DD′+FF′.
有S△PGE=S△PGD+S△PGF.
两边各扩大3倍,有S△PBE=S△PAD+S△PCF.
例4.如果三角形三边的平方成等差数列,那么该三角形和由它的三条中线围成的新三角形相似.其逆亦真.
分析:将△ABC简记为△,由三中线AD,BE,CF围成的三角形简记为△′.G为重心,连DE到H,使EH=DE,连HC,HF,则△′就是△HCF.
(1)a2,b2,c2成等差数列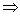 △∽△′.
△∽△′.
若△ABC为正三角形,易证△∽△′.
不妨设a≥b≥c,有
CF=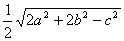 ,
,
BE=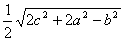 ,
,
AD=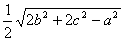 .
.
将a2+c2=2b2,分别代入以上三式,得
CF= ,BE=
,BE=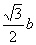 ,AD=
,AD=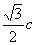 .
.
∴CF:BE:AD = :
: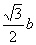 :
: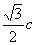
=a:b:c.
故有△∽△′.
(2)△∽△′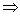 a2,b2,c2成等差数列.
a2,b2,c2成等差数列.
当△中a≥b≥c时,
△′中CF≥BE≥AD.
∵△∽△′,
∴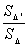 =(
=(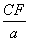 )2.
)2.
据“三角形的三条中线围成的新三角形面积等于原三角形面积的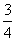 ”,有
”,有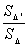 =
=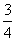 .
.
∴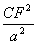 =
=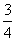
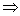 3a2=4CF2=2a2+b2-c2
3a2=4CF2=2a2+b2-c2
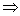 a2+c2=2b2.
a2+c2=2b2.
三、垂心
三角形三条高的交战,称为三角形的垂心.由三角形的垂心造成的四个等(外接)圆三角形,给我们解题提供了极大的便利.
例5.设A1A2A3A4为⊙O内接四边形,H1,H2,H3,H4依次为
△A2A3A4,△A3A4A1,△A4A1A2,△A1A2A3的垂心.求证:H1,H2,H3,H4四点共圆,并确定出该圆的圆心位置.
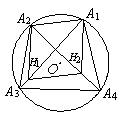 (1992,全国高中联赛)
(1992,全国高中联赛)
分析:连接A2H1,A1H2,H1H2,记圆半径
为R.由△A2A3A4知
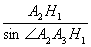 =2R
=2R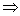 A2H1=2Rcos∠A3A2A4;
A2H1=2Rcos∠A3A2A4;
由△A1A3A4得
A1H2=2Rcos∠A3A1A4.
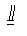 但∠A3A2A4=∠A3A1A4,故A2H1=A1H2.
但∠A3A2A4=∠A3A1A4,故A2H1=A1H2.
 易证A2H1∥A1A2,于是,A2H1 A1H2,
易证A2H1∥A1A2,于是,A2H1 A1H2,
故得H1H2 A2A1.设H1A1与H2A2的交点为M,故H1H2与A1A2关于M点成中心对称.
同理,H2H3与A2A3,H3H4与A3A4,H4H1与A4A1都关于M点成中心对称.故四边形H1H2H3H4与四边形A1A2A3A4关于M点成中心对称,两者是全等四边形,H1,H2,H3,H4在同一个圆上.后者的圆心设为Q,Q与O也关于M成中心对称.由O,M两点,Q点就不难确定了.
例6.H为△ABC的垂心,D,E,F分别是BC,CA,AB的中心.一个以H为圆心的⊙H交直线EF,FD,DE于A1,A2,B1,B2,C1,C2.
 求证:AA1=AA2=BB1=BB2=CC1=CC2.
求证:AA1=AA2=BB1=BB2=CC1=CC2.
(1989,加拿大数学奥林匹克训练题)
分析:只须证明AA1=BB1=CC1即可.设
BC=a, CA=b,AB=c,△ABC外
接圆半径为R,⊙H的半径为r.
连HA1,AH交EF于M.
A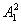 =AM2+A1M2=AM2+r2-MH2
=AM2+A1M2=AM2+r2-MH2
=r2+(AM2-MH2), ①
又AM2-HM2=(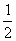 AH1)2-(AH-
AH1)2-(AH-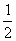 AH1)2
AH1)2
=AH·AH1-AH2=AH2·AB-AH2
=cosA·bc-AH2, ②
而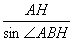 =2R
=2R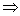 AH2=4R2cos2A,
AH2=4R2cos2A,
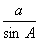 =2R
=2R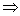 a2=4R2sin2A.
a2=4R2sin2A.
∴AH2+a2=4R2,AH2=4R2-a2. ③
由①、②、③有
A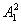 =r2+
=r2+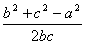 ·bc-(4R2-a2)
·bc-(4R2-a2)
=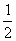 (a2+b2+c2)-4R2+r2.
(a2+b2+c2)-4R2+r2.
同理,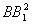 =
=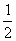 (a2+b2+c2)-4R2+r2,
(a2+b2+c2)-4R2+r2,
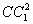 =
=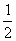 (a2+b2+c2)-4R2+r2.
(a2+b2+c2)-4R2+r2.
故有AA1=BB1=CC1.
四、内心
三角形内切圆的圆心,简称为内心.对于内心,要掌握张角公式,还要记住下面一个极为有用的等量关系:
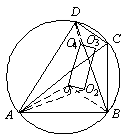 设I为△ABC的内心,射线AI交△ABC外接圆于A′,则有A ′I=A′B=A′C.换言之,点A′必是△IBC之外心(内心的等量关系之逆同样有用).
设I为△ABC的内心,射线AI交△ABC外接圆于A′,则有A ′I=A′B=A′C.换言之,点A′必是△IBC之外心(内心的等量关系之逆同样有用).
例7.ABCD为圆内接凸四边形,取
△DAB,△ABC,△BCD,
△CDA的内心O1, O2,O3,
O4.求证:O1O2O3O4为矩形.
(1986,中国数学奥林匹克集训题)
证明见《中等数学》1992;4
例8.已知⊙O内接△ABC,⊙Q切AB,AC于E,F且与⊙O内切.试证:EF中点P是△ABC之内心.
(B·波拉索洛夫《中学数学奥林匹克》)
 分析:在第20届IMO中,美国提供的一道题实际上是例8的一种特例,但它增加了条件AB=AC.当AB≠AC,怎样证明呢?
分析:在第20届IMO中,美国提供的一道题实际上是例8的一种特例,但它增加了条件AB=AC.当AB≠AC,怎样证明呢?
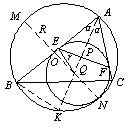 如图,显然EF中点P、圆心Q,BC中点K都在∠BAC平分线上.易知AQ=
如图,显然EF中点P、圆心Q,BC中点K都在∠BAC平分线上.易知AQ=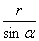 .
.
∵QK·AQ=MQ·QN,
∴QK=
=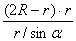 =
=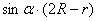 .
.
由Rt△EPQ知PQ=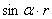 .
.
∴PK=PQ+QK=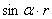 +
+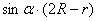 =
=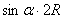 .
.
∴PK=BK.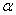

利用内心等量关系之逆定理,即知P是△ABC这内心.
五、旁心
三角形的一条内角平分线与另两个内角的外角平分线相交于
一点,是旁切圆的圆心,称为旁心.旁心常常与内心联系在一起,
旁心还与三角形的半周长关系密切.
例9.在直角三角形中,求证:r+ra+rb+rc=2p.
式中r,ra,rb,rc分别表示内切圆半径及与a,b,c相切的旁切圆半径,p表示半周.
(杭州大学《中学数学竞赛习题》)
分析:设Rt△ABC中,c为斜边,先来证明一个特性:
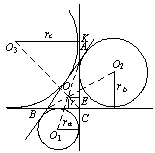 p(p-c)=(p-a)(p-b).
p(p-c)=(p-a)(p-b).
∵p(p-c)=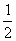 (a+b+c)·
(a+b+c)·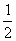 (a+b-c)
(a+b-c)
=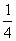 [(a+b)2-c2]
[(a+b)2-c2]
=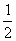 ab;
ab;
(p-a)(p-b)=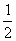 (-a+b+c)·
(-a+b+c)·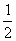 (a-b+c)
(a-b+c)
=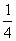 [c2-(a-b)2]=
[c2-(a-b)2]=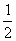 ab.
ab.
∴p(p-c)=(p-a)(p-b). ①
观察图形,可得
ra=AF-AC=p-b,
rb=BG-BC=p-a,
rc=CK=p.
而r=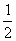 (a+b-c)
(a+b-c)
=p-c.
∴r+ra+rb+rc
=(p-c)+(p-b)+(p-a)+p
=4p-(a+b+c)=2p.
由①及图形易证.
例10.M是△ABC边AB上的任意一点.r1,r2,r分别是△AMC,△BMC,△ABC内切圆的半径,q1,q2,q分别是上述三角形在∠ACB内部的旁切圆半径.证明: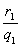 ·
·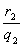 =
=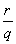 .
.
(IMO-12)
分析:对任意△A′B′C′,由正弦定理可知
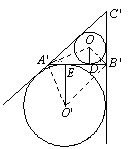 OD=OA′·
OD=OA′·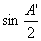
=A′B′·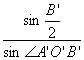 ·
·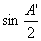
=A′B′·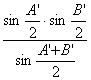 ,
,
O′E= A′B′·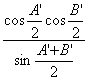 .
.
∴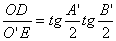 .
.
亦即有
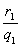 ·
·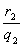 =
=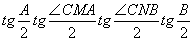
=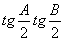 =
=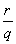 .
.
六、众心共圆
这有两种情况:(1)同一点却是不同三角形的不同的心;(2)同一图形出现了同一三角形的几个心.
例11.设在圆内接凸六边形ABCDFE中,AB=BC,CD=DE,EF=FA.试证:(1)AD,BE,CF三条对角线交于一点;
(2)AB+BC+CD+DE+EF+FA≥AK+BE+CF.
(1991,国家教委数学试验班招生试题)
分析:连接AC,CE,EA,由已知可证AD,CF,EB是△ACE的三条内角平分线,I为△ACE的内心.从而有ID=CD=DE,
IF=EF=FA,
IB=AB=BC.
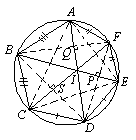
 再由△BDF,易证BP,DQ,FS是它的三条高,I是它的垂心,利用 不等式有:
再由△BDF,易证BP,DQ,FS是它的三条高,I是它的垂心,利用 不等式有:
BI+DI+FI≥2·(IP+IQ+IS).
不难证明IE=2IP,IA=2IQ,IC=2IS.
∴BI+DI+FI≥IA+IE+IC.
∴AB+BC+CD+DE+EF+FA
=2(BI+DI+FI)
≥(IA+IE+IC)+(BI+DI+FI)
=AD+BE+CF.
I就是一点两心.
例12.△ABC的外心为O,AB=AC,D是AB中点,E是△ACD的重心.证明OE丄CD.
(加拿大数学奥林匹克训练题)
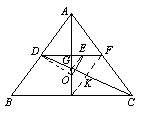 分析:设AM为高亦为中线,取AC中点
分析:设AM为高亦为中线,取AC中点
F,E必在DF上且DE:EF=2:1.设
CD交AM于G,G必为△ABC重心.
连GE,MF,MF交DC于K.易证:
DG:GK=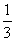 DC:(
DC:(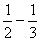 )DC=2:1.
)DC=2:1.
∴DG:GK=DE:EF GE∥MF.
GE∥MF.
∵OD丄AB,MF∥AB,
∴OD丄MF OD丄GE.但OG丄DE
OD丄GE.但OG丄DE G又是△ODE之垂心.
G又是△ODE之垂心.
易证OE丄CD.
例13.△ABC中∠C=30°,O是外心,I是内心,边AC上的D点与边BC上的E点使得AD=BE=AB.求证:OI丄DE,OI=DE.
(1988,中国数学奥林匹克集训题)
分析:辅助线如图所示,作∠DAO平分线交BC于K.
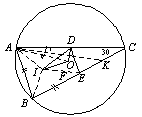 易证△AID≌△AIB≌△EIB,
易证△AID≌△AIB≌△EIB,
∠AID=∠AIB=∠EIB.
利用内心张角公式,有
∠AIB=90°+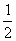 ∠C=105°,
∠C=105°,
∴∠DIE=360°-105°×3=45°.
∵∠AKB=30°+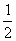 ∠DAO
∠DAO
=30°+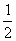 (∠BAC-∠BAO)
(∠BAC-∠BAO)
=30°+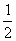 (∠BAC-60°)
(∠BAC-60°)
=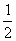 ∠BAC=∠BAI=∠BEI.
∠BAC=∠BAI=∠BEI.
∴AK∥IE.
由等腰△AOD可知DO丄AK,
∴DO丄IE,即DF是△DIE的一条高.
同理EO是△DIE之垂心,OI丄DE.
由∠DIE=∠IDO,易知OI=DE.
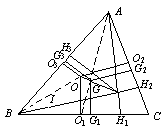 例14.锐角△ABC中,O,G,H分别是外心、重心、垂心.设外心到三边距离和为d外,重心到三边距
例14.锐角△ABC中,O,G,H分别是外心、重心、垂心.设外心到三边距离和为d外,重心到三边距
离和为d重,垂心到三边距离和为d垂.
求证:1·d垂+2·d外=3·d重.
分析:这里用三角法.设△ABC外接圆
半径为1,三个内角记为A,B,
C. 易知d外=OO1+OO2+OO3
=cosA+cosB+cosC,
∴2d外=2(cosA+cosB+cosC). ①
∵AH1=sinB·AB=sinB·(2sinC)=2sinB·sinC,
同样可得BH2·CH3.
∴3d重=△ABC三条高的和
=2·(sinB·sinC+sinC·sinA+sinA·sinB) ②
∴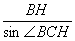 =2,
=2,
∴HH1=cosC·BH=2·cosB·cosC.
同样可得HH2,HH3.
∴d垂=HH1+HH2+HH3
=2(cosB·cosC+cosC·cosA+cosA·cosB) ③
欲证结论,观察①、②、③,
须证(cosB·cosC+cosC·cosA+cosA·cosB)+( cosA+ cosB+ cosC)=sinB·sinC+sinC·sinA+sinA·sinB.即可.
练 习 题
1.I为△ABC之内心,射线AI,BI,CI交△ABC外接圆于A′,
B′,C ′.则AA′+BB′+CC′>△ABC周长.(1982,澳大利
亚数学奥林匹克)
2.△T′的三边分别等于△T的三条中线,且两个三角形有一组角相等.求证这两个三角形相似.(1989,捷克数学奥林匹克)
3.I为△ABC的内心.取△IBC,△ICA,△IAB的外心O1,O2,O3.求证:△O1O2O3与△ABC有公共的外心.(1988,美国数学奥林匹克)
4.AD为△ABC内角平分线.取△ABC,△ABD,△ADC的外心O,O1,O2.则△OO1O2是等腰三角形.
5.△ABC中∠C<90°,从AB上M点作CA,CB的垂线MP,MQ.H是△CPQ的垂心.当M是AB上动点时,求H的轨迹.(IMO-7)
6.△ABC的边BC=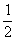 (AB+AC),取AB,AC中点M,N,G为重心,I为内心.试证:过A,M,N三点的圆与直线GI相切.(第27届莫斯科数学奥林匹克)
(AB+AC),取AB,AC中点M,N,G为重心,I为内心.试证:过A,M,N三点的圆与直线GI相切.(第27届莫斯科数学奥林匹克)
7.锐角△ABC的垂心关于三边的对称点分别是H1,H2,H3.已知:H1,H2,H3,求作△ABC.(第7届莫斯科数学奥林匹克)
8.已知△ABC的三个旁心为I1,I2,I3.求证:△I1I2I3是锐角三角形.
9.AB,AC切⊙O于B,C,过OA与BC的交点M任作⊙O的弦EF.求证:(1)△AEF与△ABC有公共的内心;(2)△AEF与△ABC有一个旁心重合.
三角形五心及其性质延伸
1.内心:三角形三条内角平分线的交点,也是三角形内切圆的圆心。
角平分线性质:到角两边距离相等.
内心性质:到三角形三边距离相等。
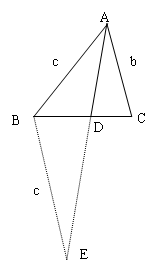 延伸:①内角平分线定理
延伸:①内角平分线定理
如图,AD为△ABC中 的平分线,则有
的平分线,则有
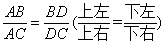
证明过程如下:
作BE//AC交其延长线于E,则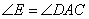 .
.
∵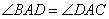 ,∴
,∴ ,
,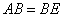 =c.
=c.
又∵BE//AC,易证△ADC ∽ △EDB, ∴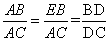 ,得证。
,得证。
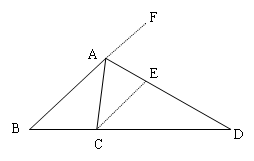 ②外角平分线定理
②外角平分线定理
如图,AD为△ABC的外角平分线,交BC
延长线于D,则有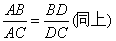
证明过程如下:
作CE//AB交AD于E,则 .∵
.∵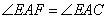 ,
,
∴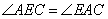 ,
,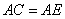 .
.
又∵CE//AB,易证△ADB ∽ △EDC, ∴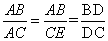 ,得证。
,得证。
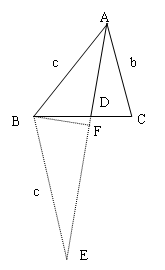 ③三角形内角平分线长公式
③三角形内角平分线长公式
如图,AD为△ABC中 的平分线,则有
的平分线,则有
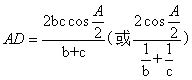
证明过程如下:
作BE//AC交其延长线于E,BF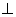 AE交其于F。
AE交其于F。
由前文的内角平分线定理可知,△ADC ∽ △EDB, ∴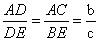 .
.
又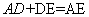 ,即
,即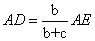 .而△ABE为等腰三角形, BF
.而△ABE为等腰三角形, BF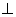 AE,
AE,
∴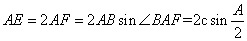 ,∴
,∴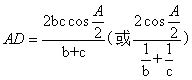 .
.
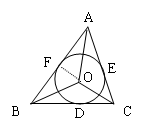 ④内心到三边距离r(三角形内切圆半径)
④内心到三边距离r(三角形内切圆半径)
设三角形面积为S,则有

证明过程如下:
连接OA,OB,OC. ∵相切,∴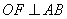 ,即S△AOB =
,即S△AOB = 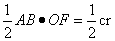 ,同理
,同理
S△AOC = 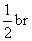 ,S△BOC =
,S△BOC = 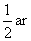 .又∵S=S△AOB + S△AOC + S△BOC ,即S=
.又∵S=S△AOB + S△AOC + S△BOC ,即S= 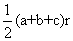 ,
,
∴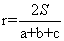 .
.
2.重心:三角形三条中线交点
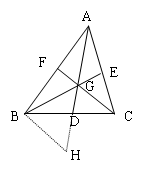 中线性质:将三角形面积等分成两部分.
中线性质:将三角形面积等分成两部分.
重心性质:分三角形的中线两段长比例为2:1(长:短)
如图:AD,BE,CF为△ABC三条中线,G为其重心,则有

证明过程如下:
作BH//FC交AD延长线于H,易证△GDC ≌ △HDB,∴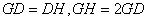
又∵BH//FG,F为AB中点,∴G也为AH中点,即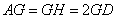 ,
,
∴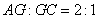 ,其他同证.
,其他同证.
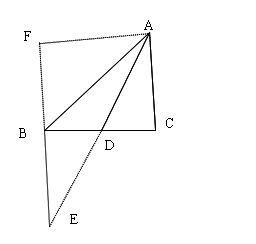
延伸:三角形中线长公式
如图,AD为△ABC的中线,则有
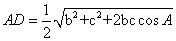
证明过程如下:
作BE//AC交AD延长线于E,易证△ADC ≌ △EDB,
∴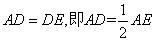 ,∵BE//AC,∴
,∵BE//AC,∴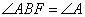 。作AF
。作AF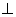 EB交其
EB交其
延长线于F。又AB=c,∴BF=AB =
=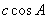 ,AF=
,AF=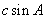 ,
,
故EF=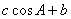 。
。
∴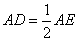 =
=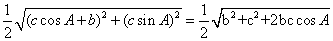
 3.外心:三角形三边垂直平分线的交点,三角形外接圆圆心。
3.外心:三角形三边垂直平分线的交点,三角形外接圆圆心。
垂直平分线性质:到线段两端点距离相等。
外心性质:到三角形三个顶点距离相等。
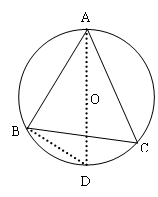
内心到三顶点距离R(三角形外接圆半径)
R= 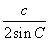 (某边除以它对角正弦的2倍)
(某边除以它对角正弦的2倍)
证明过程于下:
连接AO并延长交圆O于D,则AD为圆直径,AD=2R.
又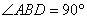 (直径所对的圆周角是
(直径所对的圆周角是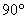 ),AB=c,
),AB=c,  (同弧AB所对的圆周角相等),∴AD=
(同弧AB所对的圆周角相等),∴AD= 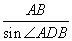 ,即2R
,即2R 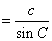 , R=
, R= 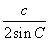 .
.
延伸①:正弦定理
由于R= 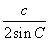 ,同理易证
,同理易证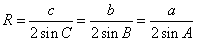 ,变形得到
,变形得到
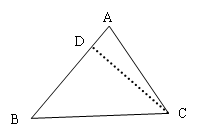 正弦定理:
正弦定理: 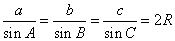 (每边除以它所对角的正弦为2R)
(每边除以它所对角的正弦为2R)
延伸②:余弦定理
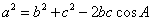 (
(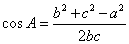 )
)
证明过程如下:
作CD 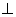 AB交其于D,∴
AB交其于D,∴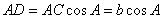 ,BD=
,BD= 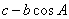 ,
,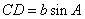 ,又
,又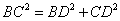 ,即
,即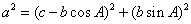 =
=
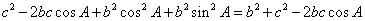 ,其他边角也同求
,其他边角也同求
4.旁心:三角形一个内角平分线与另外两个外角的平分线的交点。
旁心性质:三角形的四心(内心、重心、垂心、外心)只有一个,
 但旁心有三个,旁心到三角形三边所在直线距离相等。
但旁心有三个,旁心到三角形三边所在直线距离相等。
证明过程如下:
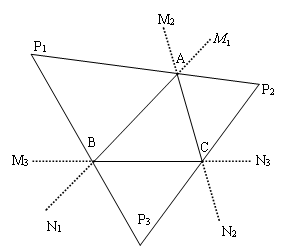
如图,P1、P2、P3为△ABC三个旁心。
以P1为例,P1在 平分线上,
平分线上,
∴P1到AB、AM2距离相等,即P1到
AB、AC所在直线M1N1、M2N2距离相等,
同理,P1在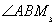 平分线上,∴P1到AB、BM3距离相等,即P1到AB、BC所在直线M1N1、M3N3距离相等,故得到旁心到三边所在直线距离相等。
平分线上,∴P1到AB、BM3距离相等,即P1到AB、BC所在直线M1N1、M3N3距离相等,故得到旁心到三边所在直线距离相等。
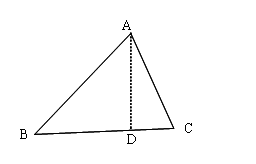
补充:三角形面积公式
① 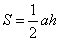 (
(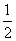 底
底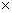 高)
高)
② 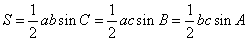
(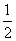 某角的正弦值乘以它两边长度的积)
某角的正弦值乘以它两边长度的积)
证明过程如下:
作AD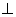 BC,则
BC,则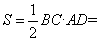
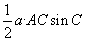
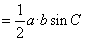 ,得证,其他边角同理可求。
,得证,其他边角同理可求。
-
相似三角形知识点总结】
1.比例线段的有关概念:在比例式ab?cd(a:b?c:d)中,a、d叫外项,b、c叫内项,a、c叫前项,b、d叫后项,d叫第四比…
-
三角形知识点总结(完)
三角形知识点全面总结1、三角形全等的性质及判定全等三角形的对应边相等,对应角也相等判定:SSS、SAS、ASA、AAS、HL(Rt…
-
三角形知识点总结(完)
三角形1、三角形全等的性质及判定全等三角形的对应边相等,对应角也相等判定:SSS、SAS、ASA、AAS、HL(Rt△≌Rt△)2…
-
三角形知识点总结
第一章图形的初步认识考点一、线段垂直平分线,角的平分线,垂线1、线段垂直平分线的性质定理及逆定理垂直于一条线段并且平分这条线段的直…
-
全等三角形知识点总结
定义能够完全重合的两个三角形称为全等三角形。(注:全等三角形是相似三角形中的特殊情况)当两个三角形完全重合时,互相重合的顶点叫做对…
-
人教版四年级下册第五章三角形的知识点总结和例题讲解
一知识点梳理1、三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连或重合),叫三角形。2、从三角形的一个顶点到它的对边做…
-
初中数学知识点总结(几何部分)
初中数学知识点(几何部分)1过两点有且只有一条直线2两点之间线段最短3同角或等角的补角相等4同角或等角的余角相等5过一点有且只有一…
-
三角形知识点总结(完)
三角形知识点全面总结1、三角形全等的性质及判定全等三角形的对应边相等,对应角也相等判定:SSS、SAS、ASA、AAS、HL(Rt…
-
三角形知识总结(初中)
三角形三角形的定义:由不在同一直线上的三条线条首尾顺次相接所组成的图形叫做三角形.三角形的三边关系:▲三角形任意两边之和大于第三边…
-
【人教版】初中数学九年级知识点总结:27相似[1]
人教版初中数学九年级知识点总结27相似编者按相似以及相似三角形是初中数学的基础内容也是重要内容运用相似三角形求解线段和角的问题是常…
-
三角形知识总结
第五章三角形一、知识要点:1、三角形的有关概念(1)三角形的定义由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形,它…