线性代数知识点总结
线性代数知识点总结
第一章 行列式
二三阶行列式
N阶行列式:行列式中所有不同行、不同列的n个元素的乘积的和 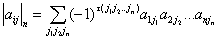
(奇偶)排列、逆序数、对换
行列式的性质:①行列式行列互换,其值不变。(转置行列式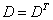 )
)
②行列式中某两行(列)互换,行列式变号。
推论:若行列式中某两行(列)对应元素相等,则行列式等于零。
③常数k乘以行列式的某一行(列),等于k乘以此行列式。
推论:若行列式中两行(列)成比例,则行列式值为零;
推论:行列式中某一行(列)元素全为零,行列式为零。
④行列式具有分行(列)可加性
⑤将行列式某一行(列)的k倍加到另一行(列)上,值不变
行列式依行(列)展开:余子式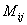 、代数余子式
、代数余子式
定理:行列式中某一行的元素与另一行元素对应余子式乘积之和为零。
克莱姆法则:
非齐次线性方程组 :当系数行列式 时,有唯一解:
时,有唯一解:
齐次线性方程组 :当系数行列式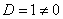 时,则只有零解
时,则只有零解
逆否:若方程组存在非零解,则D等于零
特殊行列式:
①转置行列式:
②对称行列式:
③反对称行列式: 奇数阶的反对称行列式值为零
奇数阶的反对称行列式值为零
④三线性行列式: 方法:用
方法:用 把
把 化为零,。。化为三角形行列式
化为零,。。化为三角形行列式
⑤上(下)三角形行列式:
行列式运算常用方法(主要)
行列式定义法(二三阶或零元素多的)
化零法(比例)
化三角形行列式法、降阶法、升阶法、归纳法、
第二章 矩阵
矩阵的概念: (零矩阵、负矩阵、行矩阵、列矩阵、n阶方阵、相等矩阵)
(零矩阵、负矩阵、行矩阵、列矩阵、n阶方阵、相等矩阵)
矩阵的运算:加法(同型矩阵)---------交换、结合律
数乘 ---------分配、结合律
---------分配、结合律
乘法 注意什么时候有意义
注意什么时候有意义
一般AB=BA,不满足消去律;由AB=0,不能得A=0或B=0
转置

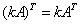
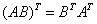 (反序定理)
(反序定理)
方幂:

几种特殊的矩阵:对角矩阵:若AB都是N阶对角阵,k是数,则kA、A+B、 AB都是n阶对角阵
数量矩阵:相当于一个数(若……)
单位矩阵、上(下)三角形矩阵(若……)
对称矩阵
反对称矩阵
阶梯型矩阵:每一非零行左数第一个非零元素所在列的下方 都是0
分块矩阵:加法,数乘,乘法:类似,转置:每块转置并且每个子块也要转置
注:把分出来的小块矩阵看成是元素
逆矩阵:设A是N阶方阵,若存在N阶矩阵B的AB=BA=I则称A是可逆的,  (非奇异矩阵、奇异矩阵|A|=0、伴随矩阵)
(非奇异矩阵、奇异矩阵|A|=0、伴随矩阵)
初等变换1、交换两行(列)2.、非零k乘某一行(列)3、将某行(列)的K 倍加到另一行(列)初等变换不改变矩阵的可逆性 初等矩阵都可逆
初等矩阵:单位矩阵经过一次初等变换得到的(对换阵 倍乘阵 倍加阵)
等价标准形矩阵
矩阵的秩r(A):满秩矩阵 降秩矩阵 若A可逆,则满秩
若A是非奇异矩阵,则r(AB)=r(B)
初等变换不改变矩阵的秩
求法:1定义2转化为标准式或阶梯形
矩阵与行列式的联系与区别:
都是数表;行列式行数列数一样,矩阵不一样;行列式最终是一个数,只要值相等,就相等,矩阵是一个数表,对应元素相等才相等;矩阵 ,行列式
,行列式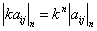
逆矩阵注: ①AB=BA=I则A与B一定是方阵 ②BA=AB=I则A与B一定互逆;
①AB=BA=I则A与B一定是方阵 ②BA=AB=I则A与B一定互逆;
③不是所有的方阵都存在逆矩阵;④若A可逆,则其逆矩阵是唯一的。
矩阵的逆矩阵满足的运算律:
1、可逆矩阵A的逆矩阵也是可逆的,且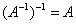
2、可逆矩阵A的数乘矩阵kA也是可逆的,且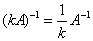
3、可逆矩阵A的转置 也是可逆的,且
也是可逆的,且
4、两个可逆矩阵A与B的乘积AB也是可逆的,且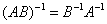
但是两个可逆矩阵A与B的和A+B不一定可逆,即使可逆,但
A为N阶方阵,若|A|=0,则称A为奇异矩阵,否则为非奇异矩阵。
5、若A可逆,则
伴随矩阵:A为N阶方阵,伴随矩阵: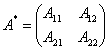 (代数余子式)
(代数余子式)
特殊矩阵的逆矩阵:(对1和2,前提是每个矩阵都可逆)
1、分块矩阵 则
则
2、准对角矩阵 , 则
, 则
3、  4、
4、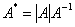 (A可逆)
(A可逆)
5、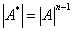 6、
6、 (A可逆)
(A可逆)
7、 8、
8、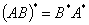
判断矩阵是否可逆:充要条件是 ,此时
,此时
求逆矩阵的方法:
定义法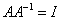
伴随矩阵法
初等变换法 只能是行变换
只能是行变换
初等矩阵与矩阵乘法的关系:
设 是m*n阶矩阵,则对A的行实行一次初等变换得到的矩阵,等于用同等的m阶初等矩阵左乘以A:对A的列实行一次初等变换得到的矩阵,等于用同种n阶初等矩阵右乘以A (行变左乘,列变右乘)
是m*n阶矩阵,则对A的行实行一次初等变换得到的矩阵,等于用同等的m阶初等矩阵左乘以A:对A的列实行一次初等变换得到的矩阵,等于用同种n阶初等矩阵右乘以A (行变左乘,列变右乘)
第三章 线性方程组
消元法 非齐次线性方程组:增广矩阵→简化阶梯型矩阵
r(AB)=r(B)=r 当r=n时,有唯一解;当 时,有无穷多解
时,有无穷多解
r(AB) r(B),无解
r(B),无解
齐次线性方程组:仅有零解充要r(A)=n有非零解充要r(A)
当齐次线性方程组方程个数<未知量个数,一定有非零解
当齐次线性方程组方程个数=未知量个数,有非零解充要|A|=0
齐次线性方程组若有零解,一定是无穷多个
N维向量:由n个实数组成的n元有序数组。希腊字母表示(加法数乘)
特殊的向量:行(列)向量,零向量θ,负向量,相等向量,转置向量
向量间的线性关系: 线性组合或线性表示
向量组间的线性相关(无):定义
向量组的秩:极大无关组(定义P188)
定理:如果 是向量组
是向量组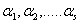 的线性无关的部分组,则它是 极大无关组的充要条件是:
的线性无关的部分组,则它是 极大无关组的充要条件是: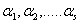 中的每一个向量都可由
中的每一个向量都可由 线性表出。
线性表出。
秩:极大无关组中所含的向量个数。
定理:设A为m*n矩阵,则 的充要条件是:A的列(行)秩为r。
的充要条件是:A的列(行)秩为r。
现性方程组解的结构:齐次非齐次、基础解系
线性组合或线性表示注:两个向量αβ,若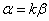 则α是β线性组合
则α是β线性组合
单位向量组
任意向量都是单位向量组的线性组合
零向量是任意向量组的线性组合
任意向量组中的一个都是他本身的线性组合
向量组间的线性相关(无)注: n个n维单位向量组一定是线性无关
一个非零向量是线性无关,零向量是线性相关
含有零向量的向量组一定是线性相关
若两个向量成比例,则他们一定线性相关
向量β可由 线性表示的充要条件是
线性表示的充要条件是
判断是否为线性相关的方法:
1、定义法:设 ,求
,求 (适合维数低的)
(适合维数低的)
2、向量间关系法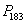 :部分相关则整体相关,整体无关则部分无关
:部分相关则整体相关,整体无关则部分无关
3、分量法(n个m维向量组) :线性相关(充要)
:线性相关(充要)
线性无关(充要)
推论①当m=n时,相关,则 ;无关,则
;无关,则
②当m
推广:若向量 组线性无关,则当s为奇数时,向量组
组线性无关,则当s为奇数时,向量组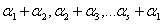 也线性无关;当s为偶数时,向量组也线性相关。
也线性无关;当s为偶数时,向量组也线性相关。
定理:如果向量组 线性相关,则向量
线性相关,则向量 可由向量组
可由向量组 线性表出,且 表示法唯一的充分必要条件是
线性表出,且 表示法唯一的充分必要条件是 线性无关。
线性无关。
极大无关组注:向量组的极大无关组不是唯一的,但他们所含向量的个数是确定的;
不全为零的向量组的极大无关组一定存在;
无关的向量组的极大无关组是其本身;
向量组与其极大无关组是等价的。
齐次线性方程组(I)解的结构:解为
(I)的两个解的和 仍是它的解;
仍是它的解;
(I)解的任意倍数 还是它的解;
还是它的解;
(I)解的线性组合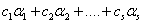 也是它的解,
也是它的解, 是任意常数。
是任意常数。
非齐次线性方程组(II)解的结构:解为
(II)的两个解的差 仍是它的解;
仍是它的解;
若 是非齐次线性方程组AX=B的一个解,v是其导出组AX=O的一个解,则u+v是(II)的一个解。
是非齐次线性方程组AX=B的一个解,v是其导出组AX=O的一个解,则u+v是(II)的一个解。
定理:
如果齐次线性方程组的系数矩阵A的秩 ,则该方程组的基础解系存在,且在每个基础解系中,恰含有n-r个解。
,则该方程组的基础解系存在,且在每个基础解系中,恰含有n-r个解。
若 是非齐次线性方程组AX=B的一个解,v是其导出组AX=O的全部解,则u+v是(II)的全部解。
是非齐次线性方程组AX=B的一个解,v是其导出组AX=O的全部解,则u+v是(II)的全部解。
第四章 向量空间
向量的内积 实向量
定义:(α,β)=
性质:非负性、对称性、线性性
(α,kβ)=k(α,β);
(kα,kβ)= (α,β);
(α,β);
(α+β, )=(α,
)=(α, )+(α,
)+(α, )+(β,
)+(β, )+(β,
)+(β, );
);

 ,
,
向量的长度
 的充要条件是α=0;α是单位向量的充要条件是(α,α)=1
的充要条件是α=0;α是单位向量的充要条件是(α,α)=1
单位化
向量的夹角
正交向量:αβ是正交向量的充要条件是(α,β)=0
正交的向量组必定线性无关
正交矩阵:n阶矩阵A 
性质:1、若A为正交矩阵,则A可逆,且 ,且
,且 也是正交矩阵;
也是正交矩阵;
2、若A为正交矩阵,则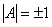 ;
;
3、若A、B为同阶正交矩阵,则AB也是正交矩阵;
4、n阶矩阵A=( )是正交矩阵的充要条件是A的列(行)向量组是 标准正交向量;
)是正交矩阵的充要条件是A的列(行)向量组是 标准正交向量;
第五章 矩阵的特征值和特征向量
特征值、特征向量
A是N阶方阵,若数 使AX=
使AX= X,即(
X,即( I-A)=0有非零解,则称
I-A)=0有非零解,则称 为A的一 个特征值,此时,非零解称为A的属于特征值
为A的一 个特征值,此时,非零解称为A的属于特征值 的特征向量。
的特征向量。
|A|=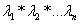
注: 1、AX= X
X
2、求特征值、特征向量的方法
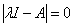 求
求 将
将 代入(
代入( I-A)X=0求出所有非零解
I-A)X=0求出所有非零解
3、对于不同的矩阵,有重根、单根、复根、实根(主要学习的)
特殊: 的特征向量为任意N阶非零向量或
的特征向量为任意N阶非零向量或
4、特征值: 若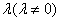 是A的特征值
是A的特征值
则 --------
--------
则 --------
--------
则 --------
--------
若 =A则-----------
=A则----------- =0或1
=0或1
若 =I则-----------
=I则----------- =-1或1
=-1或1
若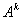 =O则----------
=O则---------- =0
=0
迹tr(A ):迹(A)=
性质:
1、N阶方阵可逆的充要条件是A的特征值全是非零的
2、A与 有相同的特征值
有相同的特征值
3、N阶方阵A的不同特征值所对应的特征向量线性无关
4、5、P281
相似矩阵
定义P283:A、B是N阶矩阵,若存在可逆矩阵P,满足 ,则矩阵A与B 相似,记作A~B
,则矩阵A与B 相似,记作A~B
性质1、自身性:A~A,P=I
2、对称性:若A~B则B~A 


3、传递性:若A~B、B~C则A~C 
 - --
- --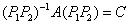
4、若AB,则A与B同(不)可逆
5、若A~B,则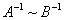
 两边同取逆,
两边同取逆,
6、若A~B,则它们有相同的特征值。 (特征值相同的矩阵不一定相似)
7、若A~B,则 初等变换不改变矩阵的秩
初等变换不改变矩阵的秩
例子: 则
则
 A=O
A=O
 A=I
A=I
 A=
A=
矩阵对角化
定理:N阶矩阵A与N阶对角形矩阵相似的充要条件是A有N个线性无关的特征向量
注:1、P与^中的 顺序一致
顺序一致
2、A~^,则^与P不是唯一的
推论:若n阶方阵A有n个互异的特征值,则 (P281)
(P281)
定理:n阶方阵 的充要条件是对于每一个
的充要条件是对于每一个 重特征根
重特征根 ,都有
,都有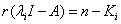
注:三角形矩阵、数量矩阵 的特征值为主对角线。
的特征值为主对角线。
约当形矩阵
约当块:形如 的n阶矩阵称为n阶约当块;
的n阶矩阵称为n阶约当块;
约当形矩阵:由若干个约当块组成的对角分块矩阵 (
( 是约当块)称为约当形矩阵。
是约当块)称为约当形矩阵。
定理:任何矩阵A都相似于一个约当形矩阵,即存在n阶可逆矩阵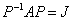 。
。
第六章 二次型
二次型与对称矩阵
只含有二次项的n元多项式f()称为一个n元二次型,简称二次型。
标准型:形如 的二次型,称为标准型。
规范型:形如 的二次型,称为规范型。
线性变换
矩阵的合同:设AB是n阶方阵,若存在一个n阶可逆矩阵C,使得 则称A与B是合同的,记作A B。
合同的性质:反身性、对称性、传递性、秩、
化二次型为标准型:配方法、做变换(二次型中不含有平方项)
-
线性代数知识点总结
《线性代数》复习提纲第二部分:基本知识一、行列式1.行列式的定义用n^2个元素aij组成的记号称为n阶行列式。(1)它表示所有可能…
-
线性代数知识点总结
线性代数知识点总结第一章行列式(一)要点1、二阶、三阶行列式2、全排列和逆序数,奇偶排列(可以不介绍对换及有关定理),n阶行列式的…
-
线性代数知识点总结
线性代数知识点总结第一章行列式(一)要点1、二阶、三阶行列式2、全排列和逆序数,奇偶排列(可以不介绍对换及有关定理),n阶行列式的…
-
线性代数知识点总结
线性代数知识点总结第一章行列式第一节二阶与三阶行列式把表达式a11a22a12a21称为a11a21a11a12所确定的二阶行列式…
-
线性代数知识点总结
第一部分基本要求计算方面四阶行列式的计算N阶特殊行列式的计算如有行和列和相等矩阵的运算包括加减数乘乘法转置逆等的混合运算求矩阵的秩…
-
线性代数总结
┏━━━━━━━━━━━━━━━━━━━━━━┓┠——※—◆—☆—★—目录—★—☆—◆—※——┨┠※※※※※※※※※※※※※※※※…
-
文科线性代数复习 总结
线性代数复习总结第一章:行列式一、概念(1)全排列与逆序数.(2)行列式:不同行不同列元素乘积的代数和(共n!项)二、性质1、经转…
-
线性代数知识点总结
线性代数知识点总结第一章行列式(一)要点1、二阶、三阶行列式2、全排列和逆序数,奇偶排列(可以不介绍对换及有关定理),n阶行列式的…
-
线性代数知识要点总结(36学时20xx0528)
线性代数知识要点总结:(20xx0528完成)第一章行列式1、二阶和三阶行列式的计算----对角线法则2、逆序与逆序数的计算方法3…
-
线性代数知识点总结
线性代数知识点总结第一章行列式(一)要点1、二阶、三阶行列式2、全排列和逆序数,奇偶排列(可以不介绍对换及有关定理),n阶行列式的…
-
加油,祝你成功--线性代数完美总结版
《线性代数及其应用》一、行列式1、余子式,代数余子式2、几个定理(定理2.2,2.3,2.4)按行展开:A?ai1Ai1?ai2A…