高考数列求和方法总结与答案全解
数列求和方法总结例题和答案全解
1 直接求和
适用于等差数列或等比数列的求和(指前 项和)问题,在四个量
项和)问题,在四个量 (或
(或 ),
), 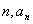 中,已知三个量时,可以求出
中,已知三个量时,可以求出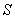
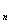 来,我们简称为“知三求和”问题.它们的求和问题可以直接利用求和公式解决.
来,我们简称为“知三求和”问题.它们的求和问题可以直接利用求和公式解决.
等差数列前 项和公式:已知
项和公式:已知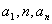 时,利用公式
时,利用公式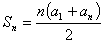 求和;
求和;
已知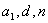 时,利用公式
时,利用公式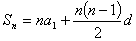 求和.
求和.
等比数列前 项和公式:已知
项和公式:已知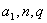 时,利用公式
时,利用公式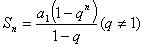 求和;
求和;
已知 时,利用公式
时,利用公式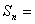
 (
(
 )求和.
)求和.
例1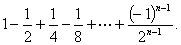
此式可看为一个等比数列的前 项和,且此等比数列首项为1,公比为
项和,且此等比数列首项为1,公比为 ,故可直接运用等比数列前
,故可直接运用等比数列前 项和公式
项和公式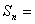
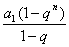 (
(
 ) 求和.
) 求和.
解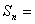
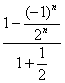

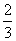


例2 一个等差数列的前 项和等于
项和等于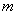 ,前
,前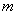 项和等于
项和等于 (其中m
(其中m
 ),试求这个数列的前
),试求这个数列的前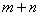 项和.
项和.
根据等差数列前 项和公式运用所需的条件最好先求出数列首项
项和公式运用所需的条件最好先求出数列首项 与公差
与公差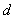 ,然后运用
,然后运用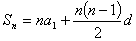 求和.
求和.
解 设这个数列的首项为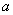 ,公差为
,公差为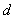 ,根据已知条件,有
,根据已知条件,有

 得
得
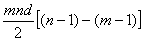 =
=
 因为
因为
所以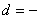
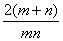

由此得 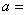
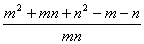 ,
,
于是,这个数列的前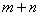 项和为
项和为
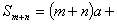


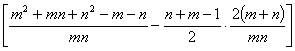
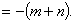
2 转化求和
适用于不是等差数列或等比数列,不便直接求其前 项和的数列.
项和的数列.
2.1反序相加法
将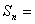
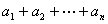 与
与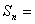
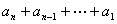 两式相加,如果得到一个常数列,其和为
两式相加,如果得到一个常数列,其和为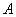 ,那么
,那么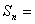


例3已知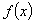 满足
满足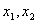
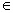
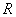 ,当
,当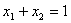 时,
时, ,若
,若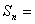
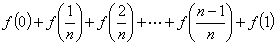
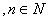
 求
求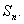
由 知只要自变量
知只要自变量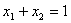 即成立,又知
即成立,又知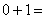 1
1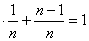 ,…,则易求
,…,则易求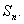
解 因为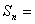
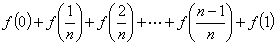 , ①
, ①
所以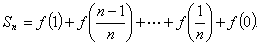 ②
②
①+②,得
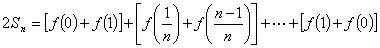

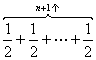

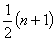

所以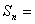
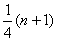

2.2错项相减法
如果数列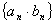 中的
中的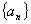 和
和 分别是等差数列和等比数列且等比数列公比为
分别是等差数列和等比数列且等比数列公比为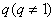 ,那么
,那么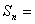
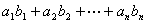 与
与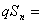
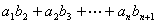 两式“错项相减”可以求出
两式“错项相减”可以求出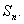
例4求和:1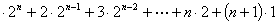

数列2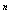 ,2
,2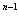 ,2
,2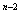 ,…,2,1与1,2,3,…,
,…,2,1与1,2,3,…, ,
, 分别是等比数列(
分别是等比数列(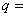
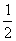 )与等差数列(
)与等差数列(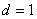 ),可考虑用“错项相减法”求和.
),可考虑用“错项相减法”求和.
解 令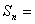 1
1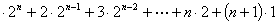 ①
①
则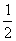
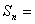 1
1 +
+ ②
②
①-②,得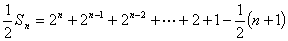
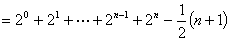

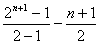

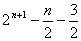 .
.
则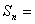
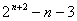 .
.
2.3组合数法
原数列各项可写成组合数形式,则可利用公式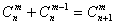 求解.
求解.
例5求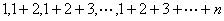 的和
的和
由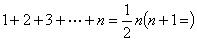
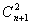 知可利用“组合数法”求和
知可利用“组合数法”求和
解 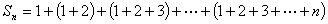
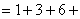
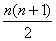



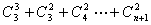
 …
…

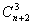

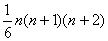 .
.
3 裂项求和
将数列的每一项分裂成两项之差,如果求数列的前 项和时,除首尾若干项外,其余各项可以交叉相消.
项和时,除首尾若干项外,其余各项可以交叉相消.
例6求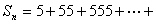
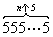
此数列



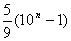 故知拆项后是一个等比数列.
故知拆项后是一个等比数列.
解 因为



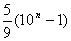 ,
,
所以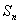

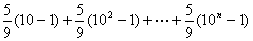




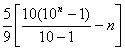

 .
.
例7 求证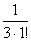

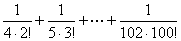 <
<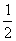
此为分数数列求和问题,仍然用裂项求和法,难点在于分母出现了阶乘,为此,需将数列的第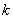 项作一些恒等变形,以便将其分裂为两项之差.
项作一些恒等变形,以便将其分裂为两项之差.
解 因为 (
(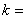
 )
)
所以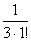

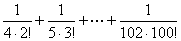

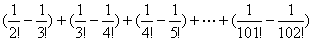

 <
<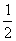 .
.
4 归纳求和
针对可猜想出其前 项和的数列.
项和的数列.
4.1直接利用归纳法
猜测出数列前n项和的形式,直接利用数学归纳法证明结论
例8在一个圆的直径两端写上自然数1,将此直径分得的两个半圆都对分,在每个分点上写上该点相邻两数之和,然后把分得的四个 圆周各自对分,在所分点上写上该点相邻两数之和,如此继续下去,问这样做第
圆周各自对分,在所分点上写上该点相邻两数之和,如此继续下去,问这样做第 步之后,圆周所有分点上之和的和
步之后,圆周所有分点上之和的和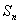 是多少?
是多少?
由题意知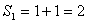 ,
,
 ,
,
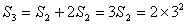 ,
,
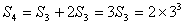 ,
,
由此可猜想出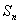

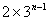 ,则可利用数学归纳法证明.
,则可利用数学归纳法证明.
解 由题意有
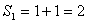 ,
,
 ,
,
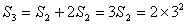 ,
,
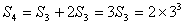 ,
,
故猜想S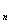 =
=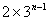 ,下面利用数学归纳法给予严格的证明.
,下面利用数学归纳法给予严格的证明.
当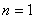 时,命题显然成立;
时,命题显然成立;
设当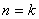 时,命题成立,则
时,命题成立,则 ;
;
当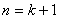 时,
时,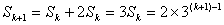 .
.
则证出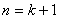 时命题成立,从而证明对所有的自然数
时命题成立,从而证明对所有的自然数 都成立.
都成立.
4.2待定归纳法
解决与自然数有关的某一问题,首先应对结论的代数形式做一正确推测,并将结论用待定系数设出来,随之令其满足数学归纳法的各个步骤,从中得到待定系数的方程或方程组,求出待定系数,即可使问题得解.
例9求数列2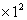 ,4
,4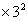 ,6
,6 ,…,2
,…,2 的前
的前 项和
项和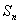 .
.
因为数列的通项公式为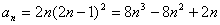 它是关于
它是关于 的多项式,与之类似的数列求和问题我们熟悉的有
的多项式,与之类似的数列求和问题我们熟悉的有
(1)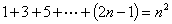
(2)1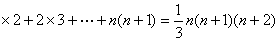
(3)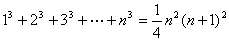
以上各式中,左端的通项公式及右端的和展开后都是关于 的多项式,对其次数进行比较便可得到这样的结论:若数列
的多项式,对其次数进行比较便可得到这样的结论:若数列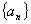 的通项公式是关于
的通项公式是关于 的多项式,则其前
的多项式,则其前 项和是比通项公式高一次的多项式.对本题来讲,因为通项公式
项和是比通项公式高一次的多项式.对本题来讲,因为通项公式
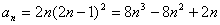
是关于 的三次多项式,所以我们猜想该数列的前
的三次多项式,所以我们猜想该数列的前 项和
项和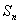 是关于
是关于 的四次多项式,故可设
的四次多项式,故可设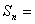
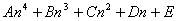 .
.
解 令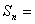
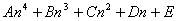 满足数学归纳法的各个步骤,
满足数学归纳法的各个步骤,
即 时上式均成立,有
时上式均成立,有
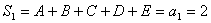 ①
①

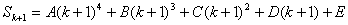
 ②
②
又因为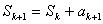
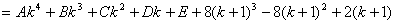
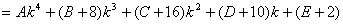 ③
③
比较②、③两式同类项系数可得
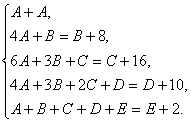
解方程得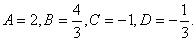 代入①式有
代入①式有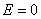 ,
,
故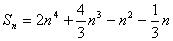
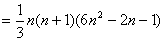
5 逐差法
针对一类高阶等差数列求和问题.某些数列的构成规律不十分明显,我们可以逐次求出它的各阶差数列,如果某一阶差数列正好是等差数列或等比数列,那么可以利用这些数列的有限和得出原数列的一个通项公式,然后再求出其前 项和
项和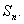
例10求数列5,6,9,16,31,62,…的前 项和
项和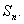
考虑数列的各差数列:
原数列:5,6,9,16,31,62,…
一阶差数列:1,3,7,15,31,…
二阶差数列:2,4,8,16,…
由于二阶差数列是等比数列,可用逐差法求数列的通项,然后再求其前 项和
项和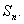
解 设原数列为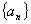 ,一阶差数列为
,一阶差数列为 ,二阶差数列为
,二阶差数列为
那么


…
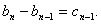
以上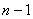 个式子相加,有
个式子相加,有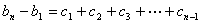
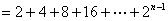

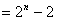 .
.
因为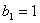 ,所以
,所以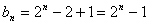 .
.
又 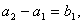

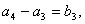
…

所以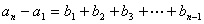
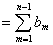

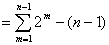
 .
.
因为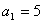 ,所以
,所以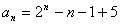
 .
.
数列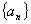 的前
的前 项和为
项和为
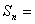
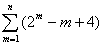
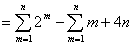
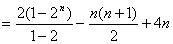
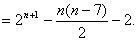
-
数列求和方法总结
数列求和的基本方法和技巧数列是高中代数的重要内容,又是学习高等数学的基础。在高考和各种数学竞赛中都占有重要的地位。数列求和是数列的…
-
数列求和方法总结
高三数学——数列求和一、本次课教学目标1、等比数列的前n项和公式推导,进一步熟练掌握等比数列的通项公式和前n项和公式;2、灵活应用…
-
数列求和方法总结
课题:数列求和的基本方法和技巧兰州三十四中----王永生教学目标:教学重点与难点:教学过程:数列是高中代数的重要内容,又是学习高等…
-
数列求和方法总结
数列求和的基本方法和技巧数列求和是数列的重要内容之一,除了等差数列和等比数列有求和公式外,大部分数列的求和都需要一定的技巧.一、利…
-
数列求和方法总结[1]
数列求和的方法和技巧数列是高中代数的重要内容,又是学习高等数学的基础。在高考和各种数学竞赛中都占有重要的地位。数列求和是数列的重要…
-
高中数列专题常见求和方法总结
专题:数列及其数列求和?重点、考点精读与点拨一、基本知识1.定义:(1).数列:按一定次序排序的一列数(2)等差数列:一般地,如果…
-
数列求和解题方法总结
高考数列求和解题方法大全数列求和问题是数列的基本内容之一,也是高考的热点和重点。由于数列求和问题题型多样,技巧性也较强,以致成为数…
-
专题--数列求和的基本方法和技巧习题
一、利用常用求和公式求和利用下列常用求和公式求和是数列求和的最基本最重要的方法.1、等差数列求和公式:Sn?n(a1?an)n(n…
-
数列 知识点总结及数列求和,通项公式的方法归纳(附例题)
数列数列的考查主要涉及数列的基本公式基本性质通项公式递推公式数列求和数列极限简单的数列不等式证明等1数列的有关概念1数列按照一定顺…
-
数列通项求和的基本方法和技巧(方法、习题、详细答案)
数列通项求和的基本方法和技巧一利用常用求和公式求和利用下列常用求和公式求和是数列求和的最基本最重要的方法1等差数列求和公式Snna…
-
数列求和方法总结
数列求和的基本方法和技巧数列求和是数列的重要内容之一,除了等差数列和等比数列有求和公式外,大部分数列的求和都需要一定的技巧.一、利…