线性代数知识点全归纳
线性代数知识点
1、行列式
1.  行列式共有
行列式共有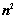 个元素,展开后有
个元素,展开后有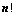 项,可分解为
项,可分解为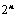 行列式;
行列式;
2. 代数余子式的性质:
①、 和
和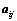 的大小无关;
的大小无关;
②、某行(列)的元素乘以其它行(列)元素的代数余子式为0;
③、某行(列)的元素乘以该行(列)元素的代数余子式为 ;
;
3. 代数余子式和余子式的关系:
4. 设 行列式
行列式 :
:
将 上、下翻转或左右翻转,所得行列式为
上、下翻转或左右翻转,所得行列式为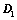 ,则
,则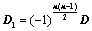 ;
;
将 顺时针或逆时针旋转
顺时针或逆时针旋转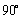 ,所得行列式为
,所得行列式为 ,则
,则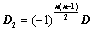 ;
;
将 主对角线翻转后(转置),所得行列式为
主对角线翻转后(转置),所得行列式为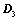 ,则
,则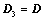 ;
;
将 主副角线翻转后,所得行列式为
主副角线翻转后,所得行列式为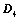 ,则
,则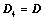 ;
;
5. 行列式的重要公式:
①、主对角行列式:主对角元素的乘积;
②、副对角行列式:副对角元素的乘积 ;
;
③、上、下三角行列式( ):主对角元素的乘积;
):主对角元素的乘积;
④、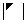 和
和 :副对角元素的乘积
:副对角元素的乘积 ;
;
⑤、拉普拉斯展开式: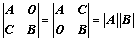 、
、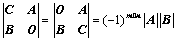
⑥、范德蒙行列式:大指标减小指标的连乘积;
⑦、特征值;
6. 对于 阶行列式
阶行列式 ,恒有:
,恒有: ,其中
,其中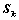 为
为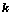 阶主子式;
阶主子式;
7. 证明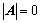 的方法:
的方法:
①、 ;
;
②、反证法;
③、构造齐次方程组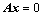 ,证明其有非零解;
,证明其有非零解;
④、利用秩,证明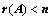 ;
;
⑤、证明0是其特征值;
2、矩阵
1.  是
是 阶可逆矩阵:
阶可逆矩阵:

 (是非奇异矩阵);
(是非奇异矩阵);

 (是满秩矩阵)
(是满秩矩阵)

 的行(列)向量组线性无关;
的行(列)向量组线性无关;
 齐次方程组
齐次方程组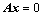 有非零解;
有非零解;

 ,
, 总有唯一解;
总有唯一解;

 与
与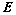 等价;
等价;

 可表示成若干个初等矩阵的乘积;
可表示成若干个初等矩阵的乘积;

 的特征值全不为0;
的特征值全不为0;

 是正定矩阵;
是正定矩阵;

 的行(列)向量组是
的行(列)向量组是 的一组基;
的一组基;

 是
是 中某两组基的过渡矩阵;
中某两组基的过渡矩阵;
2. 对于 阶矩阵
阶矩阵 :
: 无条件恒成立;
无条件恒成立;
3. 

4. 矩阵是表格,推导符号为波浪号或箭头;行列式是数值,可求代数和;
5. 关于分块矩阵的重要结论,其中均 、
、 可逆:
可逆:
若 ,则:
,则:
Ⅰ、 ;
;
Ⅱ、 ;
;
②、 ;(主对角分块)
;(主对角分块)
③、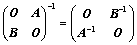 ;(副对角分块)
;(副对角分块)
④、 ;(拉普拉斯)
;(拉普拉斯)
⑤、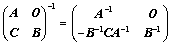 ;(拉普拉斯)
;(拉普拉斯)
3、矩阵的初等变换与线性方程组
1. 一个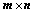 矩阵
矩阵 ,总可经过初等变换化为标准形,其标准形是唯一确定的:
,总可经过初等变换化为标准形,其标准形是唯一确定的: ;
;
等价类:所有与 等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵;
等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵;
对于同型矩阵 、
、 ,若
,若 ;
;
2. 行最简形矩阵:
①、只能通过初等行变换获得;
②、每行首个非0元素必须为1;
③、每行首个非0元素所在列的其他元素必须为0;
3. 初等行变换的应用:(初等列变换类似,或转置后采用初等行变换)
①、 若 ,则
,则 可逆,且
可逆,且 ;
;
②、对矩阵 做初等行变化,当
做初等行变化,当 变为
变为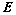 时,
时, 就变成
就变成 ,即:
,即: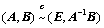 ;
;
③、求解线形方程组:对于 个未知数
个未知数 个方程
个方程 ,如果
,如果 ,则
,则 可逆,且
可逆,且 ;
;
4. 初等矩阵和对角矩阵的概念:
①、初等矩阵是行变换还是列变换,由其位置决定:左乘为初等行矩阵、右乘为初等列矩阵;
②、 ,左乘矩阵
,左乘矩阵 ,
,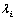 乘
乘 的各行元素;右乘,
的各行元素;右乘,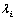 乘
乘 的各列元素;
的各列元素;
③、对调两行或两列,符号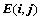 ,且
,且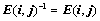 ,例如:
,例如: ;
;
④、倍乘某行或某列,符号 ,且
,且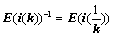 ,例如:
,例如: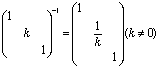 ;
;
⑤、倍加某行或某列,符号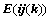 ,且
,且 ,如:
,如: ;
;
5. 矩阵秩的基本性质:
①、 ;
;
②、 ;
;
③、若 ,则
,则 ;
;
④、若 、
、 可逆,则
可逆,则 ;(可逆矩阵不影响矩阵的秩)
;(可逆矩阵不影响矩阵的秩)
⑤、 ;(※)
;(※)
⑥、 ;(※)
;(※)
⑦、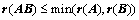 ;(※)
;(※)
⑧、如果 是
是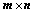 矩阵,
矩阵, 是
是 矩阵,且
矩阵,且 ,则:(※)
,则:(※)
Ⅰ、 的列向量全部是齐次方程组
的列向量全部是齐次方程组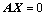 解(转置运算后的结论);
解(转置运算后的结论);
Ⅱ、
⑨、若 、
、 均为
均为 阶方阵,则
阶方阵,则 ;
;
6. 三种特殊矩阵的方幂:
①、秩为1的矩阵:一定可以分解为列矩阵(向量)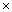 行矩阵(向量)的形式,再采用结合律;
行矩阵(向量)的形式,再采用结合律;
②、型如 的矩阵:利用二项展开式;
的矩阵:利用二项展开式;
二项展开式: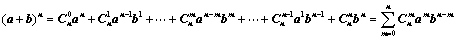 ;
;
注:Ⅰ、 展开后有
展开后有 项;
项;
Ⅱ、
Ⅲ、组合的性质: ;
;
③、利用特征值和相似对角化:
7. 伴随矩阵:
①、伴随矩阵的秩: ;
;
②、伴随矩阵的特征值: ;
;
③、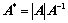 、
、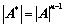
8. 关于 矩阵秩的描述:
矩阵秩的描述:
①、 ,
, 中有
中有 阶子式不为0,
阶子式不为0, 阶子式全部为0;(两句话)
阶子式全部为0;(两句话)
②、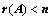 ,
, 中有
中有 阶子式全部为0;
阶子式全部为0;
③、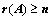 ,
, 中有
中有 阶子式不为0;
阶子式不为0;
9. 线性方程组: ,其中
,其中 为
为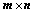 矩阵,则:
矩阵,则:
①、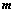 与方程的个数相同,即方程组
与方程的个数相同,即方程组 有
有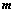 个方程;
个方程;
②、 与方程组得未知数个数相同,方程组
与方程组得未知数个数相同,方程组 为
为 元方程;
元方程;
10. 线性方程组 的求解:
的求解:
①、对增广矩阵 进行初等行变换(只能使用初等行变换);
进行初等行变换(只能使用初等行变换);
②、齐次解为对应齐次方程组的解;
③、特解:自由变量赋初值后求得;
11. 由 个未知数
个未知数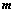 个方程的方程组构成
个方程的方程组构成 元线性方程:
元线性方程:
①、 ;
;
②、 (向量方程,
(向量方程, 为
为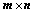 矩阵,
矩阵,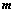 个方程,
个方程, 个未知数)
个未知数)
③、 (全部按列分块,其中
(全部按列分块,其中 );
);
④、 (线性表出)
(线性表出)
⑤、有解的充要条件: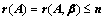 (
( 为未知数的个数或维数)
为未知数的个数或维数)
4、向量组的线性相关性
1. 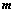 个
个 维列向量所组成的向量组
维列向量所组成的向量组 :
: 构成
构成 矩阵
矩阵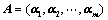 ;
;
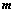 个
个 维行向量所组成的向量组
维行向量所组成的向量组 :
: 构成
构成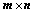 矩阵
矩阵 ;
;
含有有限个向量的有序向量组与矩阵一一对应;
2. ①、向量组的线性相关、无关  有、无非零解;(齐次线性方程组)
有、无非零解;(齐次线性方程组)
②、向量的线性表出  是否有解;(线性方程组)
是否有解;(线性方程组)
③、向量组的相互线性表示  是否有解;(矩阵方程)
是否有解;(矩阵方程)
3. 矩阵 与
与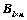 行向量组等价的充分必要条件是:齐次方程组
行向量组等价的充分必要条件是:齐次方程组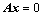 和
和 同解;(
同解;( 例14)
例14)
4.  ;(
;( 例15)
例15)
5.  维向量线性相关的几何意义:
维向量线性相关的几何意义:
①、 线性相关
线性相关 
 ;
;
②、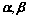 线性相关
线性相关 
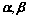 坐标成比例或共线(平行);
坐标成比例或共线(平行);
③、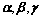 线性相关
线性相关 
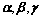 共面;
共面;
6. 线性相关与无关的两套定理:
若 线性相关,则
线性相关,则 必线性相关;
必线性相关;
若 线性无关,则
线性无关,则 必线性无关;(向量的个数加加减减,二者为对偶)
必线性无关;(向量的个数加加减减,二者为对偶)
若 维向量组
维向量组 的每个向量上添上
的每个向量上添上 个分量,构成
个分量,构成 维向量组
维向量组 :
:
若 线性无关,则
线性无关,则 也线性无关;反之若
也线性无关;反之若 线性相关,则
线性相关,则 也线性相关;(向量组的维数加加减减)
也线性相关;(向量组的维数加加减减)
简言之:无关组延长后仍无关,反之,不确定;
7. 向量组 (个数为
(个数为 )能由向量组
)能由向量组 (个数为
(个数为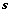 )线性表示,且
)线性表示,且 线性无关,则
线性无关,则 ;
;
向量组 能由向量组
能由向量组 线性表示,则
线性表示,则 ;
;
向量组 能由向量组
能由向量组 线性表示
线性表示
 有解;
有解; 
向量组 能由向量组
能由向量组 等价
等价
8. 方阵 可逆
可逆 存在有限个初等矩阵
存在有限个初等矩阵 ,使
,使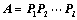 ;
;
①、矩阵行等价: (左乘,
(左乘, 可逆)
可逆) 与
与 同解
同解
②、矩阵列等价: (右乘,
(右乘, 可逆);
可逆);
③、矩阵等价: (
( 、
、 可逆);
可逆);
9. 对于矩阵 与
与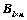 :
:
①、若 与
与 行等价,则
行等价,则 与
与 的行秩相等;
的行秩相等;
②、若 与
与 行等价,则
行等价,则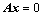 与
与 同解,
同解, 与
与 的任何对应的列向量组有相同的线性相关性;
的任何对应的列向量组有相同的线性相关性;
③、矩阵的初等变换不改变矩阵的秩;
④、矩阵 的行秩等于列秩;
的行秩等于列秩;
10. 若 ,则:
,则:
①、 的列向量组能由
的列向量组能由 的列向量组线性表示,
的列向量组线性表示, 为系数矩阵;
为系数矩阵;
②、 的行向量组能由
的行向量组能由 的行向量组线性表示,
的行向量组线性表示,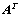 为系数矩阵;(转置)
为系数矩阵;(转置)
11. 齐次方程组 的解一定是
的解一定是 的解,【考试中可以直接作为定理使用,而无需证明】
的解,【考试中可以直接作为定理使用,而无需证明】
①、 只有零解
只有零解 只有零解;
只有零解;
②、 有非零解
有非零解 一定存在非零解;
一定存在非零解;
12. 设向量组 可由向量组
可由向量组 线性表示为:
线性表示为:
 (
( )
)
其中 为
为 ,且
,且 线性无关,则
线性无关,则 组线性无关
组线性无关 ;(
;( 与
与 的列向量组具有相同线性相关性)
的列向量组具有相同线性相关性)
(必要性: ;充分性:反证法)
;充分性:反证法)
注:当 时,
时, 为方阵,可当作定理使用;
为方阵,可当作定理使用;
13. ①、对矩阵 ,存在
,存在 ,
,
 、
、 的列向量线性无关;
的列向量线性无关;
②、对矩阵 ,存在
,存在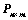 ,
,
 、
、 的行向量线性无关;
的行向量线性无关;
14.  线性相关
线性相关
 存在一组不全为0的数
存在一组不全为0的数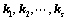 ,使得
,使得 成立;(定义)
成立;(定义)

 有非零解,即
有非零解,即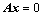 有非零解;
有非零解;

 ,系数矩阵的秩小于未知数的个数;
,系数矩阵的秩小于未知数的个数;
15. 设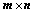 的矩阵
的矩阵 的秩为
的秩为 ,则
,则 元齐次线性方程组
元齐次线性方程组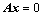 的解集
的解集 的秩为:
的秩为: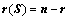 ;
;
16. 若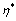 为
为 的一个解,
的一个解, 为
为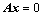 的一个基础解系,则
的一个基础解系,则 线性无关;
线性无关;
5、相似矩阵和二次型
1. 正交矩阵 或
或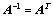 (定义),性质:
(定义),性质:
①、 的列向量都是单位向量,且两两正交,即
的列向量都是单位向量,且两两正交,即 ;
;
②、若 为正交矩阵,则
为正交矩阵,则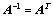 也为正交阵,且
也为正交阵,且 ;
;
③、若 、
、 正交阵,则
正交阵,则 也是正交阵;
也是正交阵;
注意:求解正交阵,千万不要忘记施密特正交化和单位化;
2. 施密特正交化:
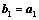 ;
;


 ;
;
3. 对于普通方阵,不同特征值对应的特征向量线性无关;
对于实对称阵,不同特征值对应的特征向量正交;
4. ①、 与
与 等价
等价 
 经过初等变换得到
经过初等变换得到 ;
;
 ,
, 、
、 可逆;
可逆;
 ,
, 、
、 同型;
同型;
②、 与
与 合同
合同 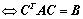 ,其中可逆;
,其中可逆;
 与
与 有相同的正、负惯性指数;
有相同的正、负惯性指数;
③、 与
与 相似
相似  ;
;
5. 相似一定合同、合同未必相似;
若 为正交矩阵,则
为正交矩阵,则

 ,(合同、相似的约束条件不同,相似的更严格);
,(合同、相似的约束条件不同,相似的更严格);
6.  为对称阵,则
为对称阵,则 为二次型矩阵;
为二次型矩阵;
7.  元二次型
元二次型 为正定:
为正定:
 的正惯性指数为
的正惯性指数为 ;
;
 与
与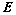 合同,即存在可逆矩阵
合同,即存在可逆矩阵 ,使
,使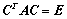 ;
;
 的所有特征值均为正数;
的所有特征值均为正数;
 的各阶顺序主子式均大于0;
的各阶顺序主子式均大于0;
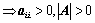 ;(必要条件)
;(必要条件)
第一章
随机事件
互斥对立加减功,条件独立乘除清;
全概逆概百分比,二项分布是核心;
必然事件随便用,选择先试不可能。
第二、三章
一维、二维随机变量
1)离散问模型,分布列表清,边缘用加乘,条件概率定联合,独立试矩阵
2)连续必分段,草图仔细看,积分是关键,密度微分算
3)离散先列表,连续后求导;分布要分段,积分画图算
第五、六章
数理统计、参数估计
正态方和卡方出,卡方相除变F,
若想得到t分布,一正n卡再相除。
样本总体相互换,矩法估计很方便;
似然函数分开算,对数求导得零蛋;
区间估计有点难,样本函数选在前;
分位维数惹人嫌,导出置信U方甜。
第七章
假设检验
检验均值用U-T,分位对称别大意;
方差检验有卡方,左窄右宽不稀奇;
不论卡方或U-T,维数减一要牢记;
代入比较临界值,拒绝必在否定域!
第二篇:考研线性代数知识点归纳
1、行列式
1. n行列式共有n2个元素,展开后有n!项,可分解为2n行列式; 2. 代数余子式的性质:
①、Aij和aij的大小无关;
②、某行(列)的元素乘以其它行(列)元素的代数余子式为0; ③、某行(列)的元素乘以该行(列)元素的代数余子式为A; 3. 代数余子式和余子式的关系:Mij?(?1)i?jAijAij?(?1)i?jMij
4. 设n行列式D:
n(n?1)将D上、下翻转或左右翻转,所得行列式为D1,则D1?(?1)
2
D; n(n?1)将D顺时针或逆时针旋转90,所得行列式为D2,则D2?(?1)2
D;
将D主对角线翻转后(转置),所得行列式为D3,则D3?D;
将D主副角线翻转后,所得行列式为D4,则D4?D; 5. 行列式的重要公式:
①、主对角行列式:主对角元素的乘积;
n(n?1)②、副对角行列式:副对角元素的乘积??(?1)
2
;
③、上、下三角行列式(?◥???◣?):主对角元素的乘积; n(n?1)④、?◤?和?◢?:副对角元素的乘积??(?1)2
;
⑤、拉普拉斯展开式:
AO?AB、
C
AC
B?ACOB
BO
?O
ABC
?(?1)mnAB
⑥、范德蒙行列式:大指标减小指标的连乘积; ⑦、特征值;
n
6. 对于n阶行列式A,恒有:?E?A??n
??(?1)kSkk?n?,其中Sk为k阶主子式;k?17. 证明A?0的方法:
①、A??A; ②、反证法;
③、构造齐次方程组Ax?0,证明其有非零解; ④、利用秩,证明r(A)?n; ⑤、证明0是其特征值;
2、矩阵
1.
A是n阶可逆矩阵:
?A?0(是非奇异矩阵);
?r(A)?n(是满秩矩阵) ?A的行(列)向量组线性无关;
?齐次方程组Ax?0有非零解; ??b?Rn,Ax?b总有唯一解;
1
?A与E等价;
?A可表示成若干个初等矩阵的乘积;
?A的特征值全不为0;
?ATA是正定矩阵;
?A的行(列)向量组是Rn的一组基;
?A是Rn中某两组基的过渡矩阵;
2. 对于n阶矩阵A:AA*?A*A?AE 无条件恒成立;
3. (A?1)*?(A*)?1
(AB)T?BTAT(A?1)T?(AT)?1(AB)*?B*A*(A*)T?(AT)* (AB)?1?B?1A?1
4. 矩阵是表格,推导符号为波浪号或箭头;行列式是数值,可求代数和;
5. 关于分块矩阵的重要结论,其中均A、B可逆:
?A1?
若A?????A2???,则: ??As?
Ⅰ、A?A1A2?A1?1?
?1Ⅱ、A??????
?1As; ?1A2???; ??As?1??O?;(主对角分块) ?1?B??A?1?AO?②、????OB???O
?O?OA?③、?????1?BO??A
?A?1?AC?④、?????OB??O
?1?1?1B?1??;(副对角分块) O??A?1CB?1??;(拉普拉斯) ?1B?O??;(拉普拉斯) B?1??A?1?AO?⑤、?????1?1?CB???BCA
3、矩阵的初等变换与线性方程组
1. 一个m?n矩阵A,总可经过初等变换化为标准形,其标准形是唯一确定的:F???Er
?OO??; O?m?n
等价类:所有与A等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵; 对于同型矩阵A、B,若r(A)?r(B)?????AB;
2. 行最简形矩阵:
①、只能通过初等行变换获得;
②、每行首个非0元素必须为1;
③、每行首个非0元素所在列的其他元素必须为0;
3. 初等行变换的应用:(初等列变换类似,或转置后采用初等行变换)
①、若(A?,?E)??(E?,?X),则A可逆,且X?A?1;
②、对矩阵(A,B)做初等行变化,当A变为E时,B就变成A?1B,即:(A,B)???(E,A?1B); ③、求解线形方程组:对于n个未知数n个方程Ax?b,如果(A,b)(E,x),则A可逆,且x?A?1b;
4. 初等矩阵和对角矩阵的概念:
2 rrc
①、初等矩阵是行变换还是列变换,由其位置决定:左乘为初等行矩阵、右乘为初等列矩阵; ??1?
②、???
???
?2
??
?,左乘矩阵A,?乘A的各行元素;右乘,?乘A的各列元素;
ii
???n?
?1
?1??1?
???
③、对调两行或两列,符号E(i,j),且E(i,j)?1?E(i,j),例如:??1???1?;
??1?1?????
?1?1?1??
11???1
④、倍乘某行或某列,符号E(i(k)),且E(i(k))?E(i()),例如:?k???
?kk??1???
?
?1
??
?(k?0); ?1??
k??k??1?1
???
⑤、倍加某行或某列,符号E(ij(k)),且E(ij(k))?1?E(ij(?k)),如:??1???1?(k?0);
??1?1?????
5. 矩阵秩的基本性质:
①、0?r(Am?n)?min(m,n);
②、r(AT)?r(A);
③、若AB,则r(A)?r(B);
④、若P、Q可逆,则r(A)?r(PA)?r(AQ)?r(PAQ);(可逆矩阵不影响矩阵的秩) ⑤、max(r(A),r(B))?r(A,B)?r(A)?r(B);(※) ⑥、r(A?B)?r(A)?r(B);(※) ⑦、r(AB)?min(r(A),r(B));(※)
⑧、如果A是m?n矩阵,B是n?s矩阵,且AB?0,则:(※)
Ⅰ、B的列向量全部是齐次方程组AX?0解(转置运算后的结论); Ⅱ、r(A)?r(B)?n
⑨、若A、B均为n阶方阵,则r(AB)?r(A)?r(B)?n;
6. 三种特殊矩阵的方幂:
①、秩为1的矩阵:一定可以分解为列矩阵(向量)?行矩阵(向量)的形式,再采用结合律;
?1ac?
?
②、型如?01b??的矩阵:利用二项展开式;
?001???
0nn?11
a?C1b?二项展开式:(a?b)n?Cnnamn?mm
?Cnab?
n?11n?1nnmmn?m
?Cnab?Cnb??Cnab;
m?0
n
注:Ⅰ、(a?b)n展开后有n?1项;
n(n?1)(n?m?1)n!
?
123mm!(n?m)!
0n
Cn?Cn?1
n
Ⅱ、Cnm?
mn?m
Ⅲ、组合的性质:Cn?Cnmmm?1
Cn ?1?Cn?Cn
?C
r?0
r
n
?2n
rr?1rCn?nCn?1;
③、利用特征值和相似对角化: 7. 伴随矩阵:
?n
?
①、伴随矩阵的秩:r(A*)??1
?0?
r(A)?n?????r(A)?n?1; r(A)?n?1
3
②、伴随矩阵的特征值:
③、A*?AA?1、A*?AA???(AX??X,A*?AA?1???A*X?A?X); n?1
8. 关于A矩阵秩的描述:
①、r(A)?n,A中有n阶子式不为0,n?1阶子式全部为0;(两句话) ②、r(A)?n,A中有n阶子式全部为0; ③、r(A)?n,A中有n阶子式不为0;
9. 线性方程组:Ax?b,其中A为m?n矩阵,则:
①、m与方程的个数相同,即方程组Ax?b有m个方程; ②、n与方程组得未知数个数相同,方程组Ax?b为n元方程;
10. 线性方程组Ax?b的求解:
①、对增广矩阵B进行初等行变换(只能使用初等行变换); ②、齐次解为对应齐次方程组的解; ③、特解:自由变量赋初值后求得;
11. 由n个未知数m个方程的方程组构成n元线性方程:
?a11x1?a12x2??a1nxn?b1????ax?ax??ax?b????2nn2①、?211222;
???am1x1?am2x2??anmxn?bn
?a11?a②、?21
???am1a12a22am2a1n??x1??b1??????a2n??x2??b2???Ax?b(向量方程,A为m?n矩阵,m个方程,n个未知数) ??????????amn??xm??bm?
?x1??b1?????xb2an?????(全部按列分块,其中???2?); ????????x?n??bn??anxn??(线性表出) ③、?a1a2④、a1x1?a2x2?
⑤、有解的充要条件:r(A)?r(A,?)?n(n为未知数的个数或维数)
4、向量组的线性相关性
1. m个n维列向量所组成的向量组A:?1,?2,,?m构成n?m矩阵A?(?1,?2,,?m);
Tm个n维行向量所组成的向量组B:?1T,?2,??1T??T??T构成m?n矩阵B??2?; ,?m?????T???m?
含有有限个向量的有序向量组与矩阵一一对应;
2. ①、向量组的线性相关、无关 ?Ax?0有、无非零解;(齐次线性方程组)
?Ax?b是否有解;(线性方程组) ②、向量的线性表出
?AX?B是否有解;(矩阵方程) ③、向量组的相互线性表示
3. 矩阵Am?n与Bl?n行向量组等价的充分必要条件是:齐次方程组Ax?0和Bx?0同解;(P101例14) 4.
5. r(ATA)?r(A);(P101例15)
n维向量线性相关的几何意义:
???0; ①、?线性相关
②、?,?线性相关 ??,?坐标成比例或共线(平行);
4
③、?,?,?线性相关 ??,?,?共面;
6. 线性相关与无关的两套定理:
若?1,?2,,?s线性相关,则?1,?2,,?s,?s?1必线性相关;
若?1,?2,,?s线性无关,则?1,?2,,?s?1必线性无关;(向量的个数加加减减,二者为对偶) 若r维向量组A的每个向量上添上n?r个分量,构成n维向量组B:
若A线性无关,则B也线性无关;反之若B线性相关,则A也线性相关;(向量组的维数加加减减) 简言之:无关组延长后仍无关,反之,不确定;
7. 向量组A(个数为r)能由向量组B(个数为s)线性表示,且A线性无关,则r?s(二版P74定理7);
向量组A能由向量组B线性表示,则r(A)?r(B);(P86定理3) 向量组A能由向量组B线性表示
?AX?B有解; ?r(A)?r(A,B)(P85定理2)
向量组A能由向量组B等价??r(A)?r(B)?r(A,B)(P85定理2推论)
Pl;
8. 方阵A可逆?存在有限个初等矩阵P1,P2,,Pl,使A?P1P2
r
①、矩阵行等价:A~B?PA?B(左乘,P可逆)?Ax?0与Bx?0同解
②、矩阵列等价:A~B?AQ?B(右乘,Q可逆); ③、矩阵等价:A~B?PAQ?B(P、Q可逆); 对于矩阵Am?n与Bl?n:
①、若A与B行等价,则A与B的行秩相等;
②、若A与B行等价,则Ax?0与Bx?0同解,且A与B的任何对应的列向量组具有相同的线性相关性; ③、矩阵的初等变换不改变矩阵的秩; ④、矩阵A的行秩等于列秩; 若Am?sBs?n?Cm?n,则:
①、C的列向量组能由A的列向量组线性表示,B为系数矩阵;
②、C的行向量组能由B的行向量组线性表示,AT为系数矩阵;(转置)
齐次方程组Bx?0的解一定是ABx?0的解,考试中可以直接作为定理使用,而无需证明; ①、ABx?0 只有零解???Bx?0只有零解;
②、Bx?0 有非零解???ABx?0一定存在非零解;
设向量组Bn?r:b1,b2,,br可由向量组An?s:a1,a2,,as线性表示为:(P110题19结论)
(b1,b2,
,br)?(a1,a2,
,as)K(B?AK)
c
9.
10.
11.
12.
其中K为s?r,且A线性无关,则B组线性无关?r(K)?r;(B与K的列向量组具有相同线性相关性) (必要性:r?r(B)?r(AK)?r(K),r(K)?r,?r(K)?r;充分性:反证法)
注:当r?s时,K为方阵,可当作定理使用;
13. ①、对矩阵Am?n,存在Qn?m,AQ?Em ?r(A)?m、Q的列向量线性无关;(P87) ②、对矩阵Am?n,存在Pn?m,PA?En ?r(A)?n、P的行向量线性无关; 14. ?1,?2,,?s线性相关
?存在一组不全为0的数k1,k2,,ks,使得k1?1?k2?2??ks?s?0成立;(定义)
?x1???x
,?s)?2??0有非零解,即Ax?0有非零解;
?????xs?
,?s)?s,系数矩阵的秩小于未知数的个数;
?(?1,?2,
?r(?1,?2,
15. 设m?n的矩阵A的秩为r,则n元齐次线性方程组Ax?0的解集S的秩为:r(S)?n?r;
16. 若?*为Ax?b的一个解,?1,?2,,?n?r为Ax?0的一个基础解系,则?*,?1,?2,,?n?r线性无关;(P111题
33结论)
5
5、相似矩阵和二次型
1. 正交矩阵?ATA?E或A?1?AT(定义),性质: ①、A的列向量都是单位向量,且两两正交,即aT?j
iaj???1i
?0i?j(i,j?1,2,n);
②、若A为正交矩阵,则A?1?AT也为正交阵,且A??1; ③、若A、B正交阵,则AB也是正交阵;
注意:求解正交阵,千万不要忘记施密特正交化和单位化;
2. 施密特正交化:(a1,a2,,ar)
b1?a1;
b2]
2?a2?[b1,a
[b]b1 1,b1
b[b1,ar]
r?ar?b[b,ar]?[br?1,ar][b1?2]b2?
1,b1][b2,b2[bbr?1; r?1,br?1]
3. 对于普通方阵,不同特征值对应的特征向量线性无关; 对于实对称阵,不同特征值对应的特征向量正交;
4. ①、A与B等价 ?A经过初等变换得到B;
?PAQ?B,P、Q可逆;
?r(A)?r(B),A、B同型;
②、A与B合同 ?CTAC?B,其中可逆;
?xTAx与xTBx有相同的正、负惯性指数; ③、A与B相似 ?P?1AP?B;
5. 相似一定合同、合同未必相似;
若C为正交矩阵,则CTAC?B?AB,(合同、相似的约束条件不同,相似的更严格);6. A为对称阵,则A为二次型矩阵;
7. n元二次型xTAx为正定:
?A的正惯性指数为n;
?A与E合同,即存在可逆矩阵C,使CTAC?E; ?A的所有特征值均为正数;
?A的各阶顺序主子式均大于0;
?aii?0,A?0;(必要条件)
6
-
线性代数知识点总结
《线性代数》复习提纲第二部分:基本知识一、行列式1.行列式的定义用n^2个元素aij组成的记号称为n阶行列式。(1)它表示所有可能…
-
线性代数知识点总结
线性代数知识点总结第一章行列式(一)要点1、二阶、三阶行列式2、全排列和逆序数,奇偶排列(可以不介绍对换及有关定理),n阶行列式的…
-
线性代数知识点总结
线性代数知识点总结第一章行列式(一)要点1、二阶、三阶行列式2、全排列和逆序数,奇偶排列(可以不介绍对换及有关定理),n阶行列式的…
-
线性代数知识点总结
线性代数知识点总结第一章行列式第一节:二阶与三阶行列式把表达式称为所确定的二阶行列式,并记作,即结果为一个数。(课本P1)同理,把…
-
线性代数知识点总结
第一部分基本要求计算方面四阶行列式的计算N阶特殊行列式的计算如有行和列和相等矩阵的运算包括加减数乘乘法转置逆等的混合运算求矩阵的秩…
-
加油,祝你成功--线性代数完美总结版
《线性代数及其应用》一、行列式1、余子式,代数余子式2、几个定理(定理2.2,2.3,2.4)按行展开:A?ai1Ai1?ai2A…
-
线性代数期末复习知识点考点总结
线性代数必考的知识点1、行列式1.n行列式共有n2个元素,展开后有n!项,可分解为2n行列式;2.代数余子式的性质:①、Aij和a…
-
20xx考研数学线性代数重点内容和典型题型总结
线性代数在考研数学中占有重要地位,必须予以高度重视.线性代数试题的特点比较突出,以计算题为主,证明题为辅,因此,万学海文数学考研辅…
-
线性代数知识点集锦
课时授课计划课次序号:8一、课题:矩阵的初等变换与初等矩阵二、课型:课堂讲授三、目的要求:熟练掌握用初等行变换把矩阵化成行阶梯形和…
-
线性代数公式总结
行列式1.n行列式共有n2个元素,展开后有n!项,可分解为2n行列式;2.代数余子式的性质:①、Aij和aij的大小无关;②、某行…
-
线性代数完美总结版
《线性代数及其应用》一、行列式1、余子式,代数余子式2、几个定理(定理2.2,2.3,2.4)按行展开:A?ai1Ai1?ai2A…