线性代数知识点汇总
第一章
AB ¹BA 即矩阵乘法不满足交换律
在矩阵乘法中,若 AB = O 不能Þ A = O 或 B = O
在矩阵乘法中, 若 AC = AD, 且 A¹O 不能Þ C = D
( A B ) T = BT AT
(1)若方阵A满足 AT = A,即 aji = aij,则称A为对称矩阵
(2) 若方阵A满足 AT = -A,即 aji = -aij,则称A为反对称矩阵。这时 aii = 0 ( i = 1, 2, … n)
任一方阵A都可以表示为一个对称矩阵与一个反对称矩阵之和
若方阵A除主对角线上的子块外,其余子块都为O,且主对角线的子块均为方阵,则称A为准对角矩阵
A11, A12,A13称为D的元素a11,a12,a13的代数余子式.
三阶行列式中去掉第 i 行第 j 列剩下元素按原来次序组成的2阶行列式记为 Mij ,称为 D中元素aij 的余子式.
Aij =(-1)i+jMij称为 aij 的代数余子式

D=D ', 其中 D ' 为 D 的转置行列式
行列式中交换某两行或两列,行列式仅改变符号

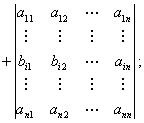
 行列式任意一行(或列)的元素与另一行(或列)的代数余子式之积的和为零
行列式任意一行(或列)的元素与另一行(或列)的代数余子式之积的和为零
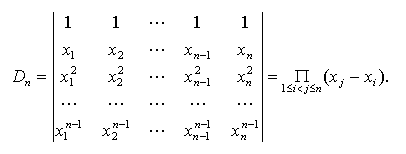
范得蒙行列式
若 |A| ¹ 0,则称方阵 A 是非奇异(非退化)的,否则,称 A 是奇异(退化)的。
若方阵A 的逆矩阵A-1 存在,则唯一.
A A*= A* A= |A | E
若A,B 均为n阶可逆矩阵,则 (AB)-1 = B-1A-1。
若A1,A2,…,Am均为n阶可逆矩阵,则 ( A1 A2 … Am)-1 = Am-1 … A2-1 A1-1
当 |A| ¹ 0,有 (A m )-1 = (A-1 ) m
 第二章
第二章
任何非零矩阵都可以用初等变换化为标准形
n阶方阵A为可逆矩阵的充要条件是A的标准形为单位矩阵
由单位矩阵 E 经过一次初等变换得到的矩阵称为初等矩阵
1.初等矩阵都是可逆矩阵,
2.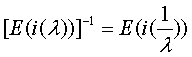 初等矩阵的逆矩阵仍然是初等矩阵
初等矩阵的逆矩阵仍然是初等矩阵
 ;
;
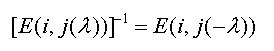
对A施行一次初等行变换,相当于在A的左侧乘以一个相应的初等矩阵;
对A施行一次初等列变换,相当于在A的右侧乘以一个相应的初等矩阵
若方阵A可逆,则存在有限个初等矩阵P1, P2,…Pm, 使A = P1 P2 … Pm
A、B都为m×n矩阵,则A~B的充要条件是存在m阶可逆矩阵P和n阶可逆矩阵Q,使得PAQ=B.
( A E )初等行变换( E A-1)
(1) A 的每个元素aij 都是A 的一个一阶子式
(2) 当A 为n 阶方阵时,n 阶子式即为 | A |
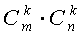 (3) 当A 为m×n 矩阵时,A共有 个k阶子式。
(3) 当A 为m×n 矩阵时,A共有 个k阶子式。
矩阵A的不为0的子式的最高阶数称为矩阵A的秩,记为r (A)。 零矩阵的秩为0,即r (O) = 0
若矩阵A中至少有一个k阶子式D不为0,而包含D的所有k+1 阶子式全为0,则r ( A ) = k。
定理2.8 对矩阵施行初等变换,矩阵的秩不变
定理2.9 一个矩阵的标准形是唯一的。

定理2.10 对于n元齐次方程组Ax=0. 设r(A) = r,则(I) r = n,有唯一解 (即零解); (II) r < n,有无穷解,即有非零解.
若r(A) ≠r(A,b),则方程组Ax=b无解。
方程组Ax=b有唯一解的充要条件是r(A) = r(A,b)=n(未知数的个数)。
当A为方阵时,方程组Ax=b有唯一解的充要条件是A的行列式不等于0,此时x=A-1b。
第三章
两个向量a = ( a1, a2, … an ), b = (b 1, b 2, … b n )相等,记 a = b ai = bi ( i = 1, 2, … , n)
向量的加法及数与向量的乘法两种运算统称为向量的线性运算。
e1 = ( 1, 0, … , 0), e2 = ( 0, 1, … , 0), … , en = ( 0, 0, … , 1) 称 e1,e2,… ,en 为 n 维单位向量组
设 n 维向量组 a1,a2,a3 线性无关 ,而 β1=α1+α2 ,β2=α2+α3, β3=α1+α3,试证向量组β1,β2,β3也线性无关.
对于m+1 个n 维向量a1 ,a2 ,…,am 和b,若存在m个数l1,l2,… ,lm,使得:b = l1a1 + l2a2 + …+ lmam 则称向量b能用向量组a1 ,a2 ,…,am线性表示,或称b是a1 ,a2 ,…,am 的线性组合,l1,l2,… ,lm 称为组合系数。
Rn 中的任一个向量a = ( x1, x2 , …, xn ) 都是单位坐标向量组的一个线性组合:a = x1e1 + x2e2 + …+ xnen

若m个向量a1 ,a2 ,…,am 中有一部分向量线性相关,则这m个向量也线性相关 (部分相关 整体相关)
包含零向量的向量组一定线性相关
若m个向量a1 ,a2 ,…,am 线性无关,则其中任一部分也线性无关。(整体无关 部分无关)
可逆矩阵的行、列向量组线性无关
m个n维向量a1 ,a2 ,…,am线性无关 r(A) = m
若m > n,则m个n维向量必线性相关 ( 因为 r (A) £ min (m , n) = n < m )
n个n维向量a1 ,a2,…,an 线性相关| A | = 0,即A降秩
n个n维向量a1,a2,…,an线性无关| A | ¹ 0,即A满秩

 设有向量组A: 如果A组能由B组线性表示且A组线性无关,则A组所含的向量个数r不大于B组所含的向量个数s,即 r £ s. 若向量组A能用B线性表示,且 r > s, 则向量组A线性相关
设有向量组A: 如果A组能由B组线性表示且A组线性无关,则A组所含的向量个数r不大于B组所含的向量个数s,即 r £ s. 若向量组A能用B线性表示,且 r > s, 则向量组A线性相关
等价的线性无关向量组含有相同个数的向量。
任意n+k(k³1)个n维向量一定线性相关。
设a1, a2, …, ar 为向量组T一个最大无关组,则任取a ÎT,a 能用a1, a2,…, ar 线性表示
一个向量组的所有最大无关组含有的向量个数都相等
向量组T 的最大无关组所含向量的个数r称为向量组T 的秩。规定:只含零向量的向量组的秩为0
将每一行看成一个向量ai = ( ai1 ai2 … ain ) ( i = 1, 2,… , m) 称为 A 的行向量,行向量组的秩称为A的行秩
r (A) = r A的行秩(或列秩)为r
设V是一个向量空间,V1 Ì V,若V1也是一个向量空间 (即对向量的两种运算封闭),则称 V1 是 V的一个子空间
注:一个向量空间 V至少有两个子空间:V及零子空间 {0},称为平凡子空间。
由a1, a2, … ,am生成的向量空间,记为 L(a1, a2, … , am )
设V为向量空间,若存在a1, a2, …, ar Î V. (1) a1, a2, …, ar 线性无关;(2) V中任一向量都可以由a1, a2, …, ar 线性表示;则称a1, a2, …, ar 为V的一组基底,简称基,r 为V的维数,并称 V 为r维向量空间 注意:向量的维数与向量空间的维数的区别
1:若将向量空间V看成向量组,其基底就是其最大无关组,其维数就是其秩2:零空间 {0} 没有基,规定其维数为0
对于Rn (1) 基本单位向量组e1, e2, …, en 是一组基,称为标准基。(2) a1 = (1, 0, 0,…, 0), a2 = (1, 1, 0,…, 0), …,an = (1, 1,…, 1) 也是基。
 a= x1a1 +x2a2 + … + xnan且组合系数 x1, x2, …, xn 唯一,称为向量a在基a1, a2, …, an 下的坐标,记为 (x1, x2, …, xn)
a= x1a1 +x2a2 + … + xnan且组合系数 x1, x2, …, xn 唯一,称为向量a在基a1, a2, …, an 下的坐标,记为 (x1, x2, …, xn)
 (al, b)= l(a, b);(a+b,g ) = (a, g)+ (b , g)(分配率);(a, a)³ 0, 且(a, a)= 0 if a = 0.(非负性)
(al, b)= l(a, b);(a+b,g ) = (a, g)+ (b , g)(分配率);(a, a)³ 0, 且(a, a)= 0 if a = 0.(非负性)
为向量a的模(或范数,长度).
 Chauchy-Schwarz不等式:向量的内积满足
Chauchy-Schwarz不等式:向量的内积满足
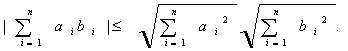 其中等号成立当且仅当向量a和 b线性相关.
其中等号成立当且仅当向量a和 b线性相关.
重要不等式;
n维欧氏空间中任意一组两两正交的向量组称为正交向量组.
若n维欧氏空间中向量a1, a2 , …, ar 是一组两两正交的非零向量, 则a1, a2 , …, ar 线性无关.
标准正交基:两两正交且 | a i| = 1, i = 1, …, r

 任何一个非零向量空间V都存在标准正交基, 且若a1, …, ar 为V的一个基, 则可通过a1, …, ar 构造出一个标准正交基.构造性证明(Schmidt正交化):
任何一个非零向量空间V都存在标准正交基, 且若a1, …, ar 为V的一个基, 则可通过a1, …, ar 构造出一个标准正交基.构造性证明(Schmidt正交化):
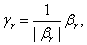 Þ Schmidt 正交化过程 则g1, g2, …, gr 是一个标准正交基.
Þ Schmidt 正交化过程 则g1, g2, …, gr 是一个标准正交基.
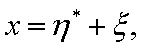
 Ax=0 的通解形式为:
Ax=0 的通解形式为:
若Ax=b有解,则其通解为: (x=k1a1+…+ kn-ran-r+a0 .)
设r(A) = r , 则方程Ax=0的基础解系中解的个数为t = n-r.
 第四章
第四章
A为正交矩阵的充要条件是A的列(行)向量都是单位向量且两两正交.
 正交变换保持向量的内积不变,从而保持向量的长度及向量间的夹角不变.
正交变换保持向量的内积不变,从而保持向量的长度及向量间的夹角不变.

若p1,p2,…,ps都是方阵A的对应于特征值λ的特征向量,则它们的任何非零线性组合k1p1+k2p2+ …+ksps也是A的对应于λ的特征向量。 矩阵的特征向量总是相对于矩阵的特征值而言的,一个特征值具有的特征向量不唯一;一个特征向量不能属于不同的特征值.

第五章
只含有平方项的二次型称为二次型的标准形(或法式).
在二次型的矩阵表示中,任给一个二次型,就唯一地确定一个对称矩阵;反之,任给一个对称矩阵,也可唯一地确定一个二次型.二次型与对称矩阵之间存在一一对应的关系.
对于二次型,我们讨论的主要问题是:寻求可逆的线性变换,将二次型化为标准形.
对于n阶矩阵A和B,如果存在n阶可逆矩阵C,使B=CTAC,就称B合同于A,记着A≌B。也称“对A进行合同变换变为B”。
一个实二次型,既可以通过正交变换化为标准形,也可以通过拉格朗日配方法化为标准形,显然,其标准形一般来说是不唯一的,但标准形中所含有的项数是确定的,项数等于二次型的秩
对称矩阵A为正定的充分必要条件是:A的特征值全为正.
对称矩阵A为正定的充分必要条件是:A的各阶主子式为正
对称矩阵A为负定的充分必要条件是:A的奇数阶主子式为负,而偶数阶主子式为正
第二篇:线性代数自考知识点汇总
行列式
1. 行列式的性质
性质1 行列式与它的转置行列式相等 .
.
性质2 互换行列式的两行(列),行列式变号.
推论1 如果行列式有两行(列)的对应元素完全相同,则此行列式的值为零.
如
性质3 行列式的某一行(列)中所有的元素都乘以同一数k ,等于用数k乘此行列式.
如
推论2 如果行列式中有两行(列)元素成比例,则此行列式的值为零.
如
性质4 若行列式的某一行(列)的元素都是两数之和,则这个行列式等于两个行列式之和.
如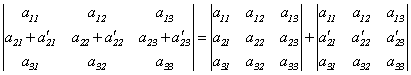
性质5 把行列式的某一行(列)的各元素乘以同一数然后加到另一行(列)对应的元素上去,行列式的值不变.
如
2. 余子式与代数余子式
在n阶行列式中,把元素 所在的第i行和第j列划去后,留下来的n-1阶行列式叫做元素
所在的第i行和第j列划去后,留下来的n-1阶行列式叫做元素 的余子式,记作
的余子式,记作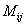 ,
, 叫做元素
叫做元素 的代数余子式.
的代数余子式.
如 ,元素
,元素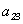 的余子式为
的余子式为 ,
,
元素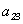 的代数余子式为
的代数余子式为 .
.
3. 行列式按行(列)展开法则
定理1 行列式的值等于它的任一行(列)的各元素与其对应的代数余子式乘积之和,即
 或
或

如

定理2 行列式任一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零,即
 或
或

4. 行列式的计算
(1)二阶行列式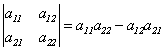
(2)三阶行列式

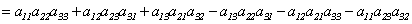
(3)对角行列式 ,
,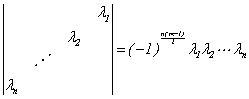
(4)三角行列式

(5)消元法:利用行列式的性质,将行列式化成三角行列式,从而求出行列式的值.
(6)降阶法:利用行列式的性质,化某行(列)只有一个非零元素,再按该行(列)展开,通过降低行列式的阶数求出行列式的值.
(7)加边法:行列式每行(列)所有元素的和相等,将各行(列)元素加到第一列(行),再提出公因式,进而求出行列式的值.
矩阵
1. 常见矩阵
1)对角矩阵:主对角线以外的元素全为0的方阵,称为对角矩阵.记作Λ.
2)单位矩阵:主对角线上的元素全为1的对角矩阵,称为单位矩阵.记作E.
3)上三角矩阵:对角线以下的元素全为0的方阵.如
4)下三角矩阵:对角线以上的元素全为0的方阵.如
5)对称矩阵:设A为n阶方阵,若 ,即
,即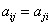 ,则称A为对称矩阵.
,则称A为对称矩阵.
6)反对称矩阵:设A为n阶方阵,若 ,即
,即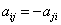 ,则称A为反对称矩阵.
,则称A为反对称矩阵.
7)正交矩阵:设A为n阶方阵,如果 或
或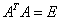 ,则称A为正交矩阵.
,则称A为正交矩阵.
2. 矩阵的加法、数乘、乘法运算
(1)矩阵的加法
如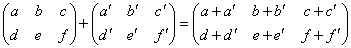
注:① 只有同型矩阵才能进行加减运算;
② 矩阵相加减就是对应元素相加减.
(2)数乘矩阵
如
注:数乘矩阵就是数乘矩阵中的每个元素.
(3)矩阵的乘法:设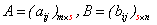 ,规定
,规定
其中
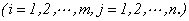
注:①左矩阵A的列数等于右矩阵B的行数;
②左矩阵A 的第i行与右矩阵B的第j列对应元素乘积的和是矩阵乘积C的元素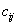 .
.
③左矩阵A的行数为乘积C的行数,右矩阵B的列数为乘积C的列数.
如行矩阵乘列矩阵是一阶方阵(即一个数),即
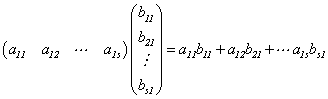
列矩阵乘行矩阵是s阶方阵,即
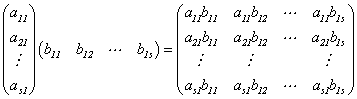
3. 逆矩阵
设n阶方阵A、B,若AB=E或BA=E,则A,B都可逆,且 .
.
(1)二阶方阵求逆,设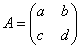 ,则
,则 (两调一除法).
(两调一除法).
(2)对角矩阵的逆 ,
,
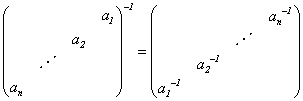 .
.
(3)分块对角阵的逆
 .
.
(4)一般矩阵求逆,初等行变换的方法: .
.
4. 方阵的行列式
由n阶方阵A的元素所构成的行列式(各元素的位置不变)叫做方阵A的行列式.记作 或det(A).
或det(A).
5. 矩阵的初等变换
下面三种变换称为矩阵的初等行(列)变换:
(1)互换两行(列);(2)数乘某行(列);(3)某行(列)的倍数加到另一行(列).
6. 初等矩阵
单位矩阵经过一次初等变换得到的矩阵,称为初等矩阵.
如 都是初等矩阵.
都是初等矩阵.
7. 矩阵的秩
矩阵A的非零子式的最高阶数,称为矩阵A的秩.记作R(A)或r(A).
求矩阵的秩的方法:
(1)定义法:找出A中最高阶的非零子式, 它的阶数即为A的秩.
(2)初等行变换法: 行阶梯形矩阵,R(A)=R(行阶梯形矩阵)=非零行的行数.
行阶梯形矩阵,R(A)=R(行阶梯形矩阵)=非零行的行数.
8. 重要公式及结论
(1)矩阵运算的公式及结论


矩阵乘法不满足交换律,即一般地AB≠AB;
矩阵乘法不满足消去律,即一般地若AB=AC,无B=C;只有当A可逆时,有B=C.
一般地若AB=O,则无A=O或B=O.
 .
.
(2)逆矩阵的公式及定理

A可逆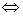 |A|≠0
|A|≠0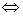 A~E(即A与单位矩阵E等价)
A~E(即A与单位矩阵E等价)
(3)矩阵秩的公式及结论

R( AB ) ≤R( A ), R( AB ) ≤R( B ).
特别地,当A可逆时,R(AB)=R(B);当B可逆时,R(AB)=R(A).
 即等价矩阵的秩相等或初等变换不改变矩阵的秩.
即等价矩阵的秩相等或初等变换不改变矩阵的秩.
9. 矩阵方程
(1)设 A 为n阶可逆矩阵,B为n×m矩阵,则矩阵方程AX=B 的解为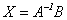 ;
;
解法:① 求出 ,再计算
,再计算 ;
;
② 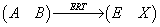 .
.
(2)设 A 为n阶可逆矩阵,B为m×n矩阵,则矩阵方程XA=B 的解为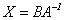 ;
;
解法:① 求出 ,再计算
,再计算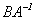 ;
;
②  .
.
10. 矩阵间的关系
(1)等价矩阵:如果矩阵A经过有限次初等变换变成矩阵B,那么称矩阵A与B等价.
即存在可逆矩阵P,Q,使得PAQ=B.
性质:等价矩阵的秩相等.
(2)相似矩阵:如果存在可逆矩阵P,使得 ,那么称A与B相似.
,那么称A与B相似.
性质:相似矩阵有相同的特征多项式,相同的特征值,相同的行列式,相同的迹.
(3)合同矩阵:如果存在可逆矩阵P,使得 ,那么称A与B合同.
,那么称A与B合同.
性质:合同矩阵的秩相等.
向量空间
1. 线性组合
(1)若α=kβ,则称向量α与β成比例.
(2)零向量O是任一向量组的线性组合.
(3)向量组中每一向量都可由该向量组线性表示.
2. 线性相关与线性无关
(1) 单独一个向量线性相关当且仅当它是零向量.
(2) 单独一个向量线性无关当且仅当它是非零向量.
(3) 两向量线性相关当且仅当两向量对应成比例.
(4) 两向量线性无关当且仅当两向量不对应成比例.
(5) 含有O向量的向量组一定线性相关.
(6) 向量组 线性相关的充分必要条件是
线性相关的充分必要条件是
① 齐次线性方程组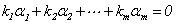 有非零解.
有非零解.
② 以向量组为列作的矩阵 的秩<向量的个数m.
的秩<向量的个数m.
(7)n个n维向量 线性相关的充分必要条件是
线性相关的充分必要条件是
以向量组为列作的行列式的值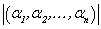 =0.
=0.
(8) 向量组 线性无关的充分必要条件是
线性无关的充分必要条件是
① 齐次线性方程组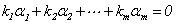 只有零解.
只有零解.
② 以向量组为列作的矩阵 的秩=向量的个数m.
的秩=向量的个数m.
(9) n个n维向量 线性无关的充分必要条件是
线性无关的充分必要条件是
以向量组为列作的行列式的值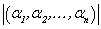 ≠0.
≠0.
(10)当m>n时,m个n维向量一定线性相关.
定理1:向量组a1 , a2 ,……, am (m≥2)线性相关的充分必要条件是向量组中至少有一个向量可由其余m-1个向量线性表示.
向量组线性无关的充分必要条件是向量组中任何一个向量都不能由其余向量线性表示.
定理2:如果向量组A:a1 , a2 ,……, ar 线性无关,而向量组a1 , a2 ,……, ar,α线性相关,则α可由A线性表示,且表示式唯一.
定理3:设向量组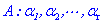 ,
,
若A线性相关,则向量组B也线性相关;反之,若向量组B线性无关,则向量组A也线性无关.
(即部分相关,则整体相关;整体无关,则部分无关).
定理4:无关组的截短组无关,相关组的接长组相关.
3. 极大无关组与向量组的秩
定义1 如果在向量组 T 中有 r 个向量 a1 , a2 ,……, ar ,满足条件:
⑴ 向量组 a1 , a2 ,……, ar 线性无关,
⑵  ,
,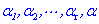 线性相关.
线性相关.
那么称向量 a1 , a2 ,……, ar 是向量组 T 的一个极大无关组.
定义2 向量组的极大无关组中所含向量的个数,称为向量组的秩.
定义3 矩阵的行向量组的秩称为矩阵的行秩;矩阵的列向量组的秩称为矩阵的列秩。
结论1 线性无关的向量组的极大无关组就是它本身。
结论2 如果向量组的秩是r ,那么该向量组的任意 r 个线性无关的向量都是它的一个极大无关组。
定理1 设向量组A:a1,a2, …,ar;及向量组B:b1,b2, …, bs,如果组A能由组B线性表示,且组A线性无关,则r≦s.
推论1 等价的向量组有相同的秩.
定理2 矩阵的秩=矩阵列向量组的秩=矩阵行向量组的秩.
4. 向量空间
定义1 设V为n维向量的集合,如果集合V非空,且集合V对于加法及乘数两种运算封闭,那么就称集合V为向量空间.
5. 基与向量在基下的坐标
定义2 设V是向量空间,如果向量组a1 , a2 ,……, ar ,满足条件:
(1)向量组 a1 , a2 ,……, ar 线性无关;
(2) ,
, 线性相关.
线性相关.
那么称向量组a1 , a2 ,……, ar是向量空间V的一个基, 基中所含向量的个数称为向量空间V的维数,记作dimV,并称V为r维向量空间.
定义3 设向量组 a1 , a2 , … , ar 是向量空间V的一个基,则V中任一向量x可唯一地表示为基的一个线性组合,即  ,
,
称有序数组 为向量x在基 a1 , a2 , … , ar下的坐标.
为向量x在基 a1 , a2 , … , ar下的坐标.
线性方程组
1. 线性方程组解的判定
(1) 线性方程组Ax=b有解的充分必要条件是它的系数矩阵A和增广矩阵(A,b)的秩相同,
即R(A)=R(A,b).
当R(A)=R(A,b)=r
① 方程组AX=b有惟一解的充分必要条件是r=n;
② 方程组AX=b有无穷多解的充分必要条件是r < n.
(2) 方程组AX= b无解的充分必要条件是R(A) ≠R(A,b).
2. 齐次线性方程组有非零解的判定
(1) 齐次方程组AX=0有非零解的充分必要条件是系数矩阵A的秩 R(A) < 未知量的个数n .
(2) 含有n个方程,n个未知量的齐次线性方程组AX=0有非零解的充分必要条件是方程组的系数行列式等于零.(即|A|=0)
(3) 齐次线性方程组AX=0中,若方程的个数m<未知量的个数n,则方程组有非零解
3. 齐次线性方程组解的性质
(1) 若 是Ax=0的解,则
是Ax=0的解,则 也是Ax=0的解;
也是Ax=0的解;
(2) 若 是Ax=0的解,则
是Ax=0的解,则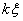 也是Ax=0的解.
也是Ax=0的解.
4. 齐次线性方程组的基础解系与通解
(1) 解空间
齐次线性方程组Ax=0的全体解向量所组成的集合,是一个向量空间,称为方程组 Ax=0的解空间.记作V,即V={ x | Ax=0,x∈R }.
(2) 基础解系
齐次方程组AX=0的解空间 V 的一个基,称为齐次方程组AX=0 的一个基础解系.
基础解系中解向量的个数是n-r(A).
方程组AX=0的任意n-r个线性无关的解都是AX=0的基础解系.
(3)齐次线性方程组的通解为 ,其中
,其中 是Ax=0的一个基础解系.
是Ax=0的一个基础解系.
5. 非齐次线性方程组解的性质
(1)若 是Ax=b的解,则
是Ax=b的解,则 是Ax=0的解;
是Ax=0的解;
即Ax=b 的任意两个解的差必是其导出组Ax=0的解.
(2)若 是Ax=b的解,
是Ax=b的解, 是Ax=0的解,则
是Ax=0的解,则 是Ax=b的解.
是Ax=b的解.
即Ax=b的任意一个解和其导出组 Ax=0 的任意一个解之和仍是 Ax=b的解.
6. 非齐次线性方程组的通解
非齐次线性方程组AX=b的通解为
其中 为对应的齐次线性方程组Ax=0的一个基础解系,
为对应的齐次线性方程组Ax=0的一个基础解系,  为非齐次线性方程组AX=b的任意一个解,称为特解.
为非齐次线性方程组AX=b的任意一个解,称为特解.
方阵的特征值
1. 向量的内积
设 ,则x,y的内积为
,则x,y的内积为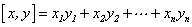 .
.
(1)向量x的长度: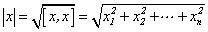
(2)非零向量的单位化:若向量 x ≠0 , 
(3)当 正交.
正交.
(4)若非零向量组中的向量两两正交,则称该向量组为正交组.
(5)若正交组中每个向量都是单位向量,则称它为标准正交组.
定理1 正交向量组必线性无关
定理2 A 为正交矩阵的充分必要条件是 A 的列(行)向量都是单位向量且两两正交.
(6)施密特正交化过程
设 是一个线性无关的向量组,
是一个线性无关的向量组,
① 正交化:令

 ;
;
② 单位化:取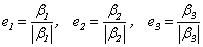 .
.
则 是与
是与 等价的标准正交组.
等价的标准正交组.
2. 特征值与特征向量
(1)方阵A的特征值 是特征方程
是特征方程 的根.
的根.
(2)三角矩阵和对角矩阵的全部特征值就是它的全部对角元.
(3)方阵和它的转置方阵有相同的特征值.
(4)设 是n阶方阵A的全部特征值,则
是n阶方阵A的全部特征值,则 ,
, .
.
即方阵A的对角线上元素之和等于A的全部特征值之和,方阵A的行列式等于A的全部特征值的乘积.
(5)若 是方阵A的特征值,则
是方阵A的特征值,则 是方阵
是方阵 的特征值. 特别地,当
的特征值. 特别地,当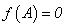 时,方阵A的特征值是
时,方阵A的特征值是 的根.
的根.
说明: ,
, .
.
例如 是方阵A的特征值,则方阵
是方阵A的特征值,则方阵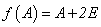 的特征值是
的特征值是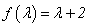 .
.
方阵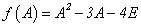 的特征值是
的特征值是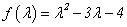 .
.
例如若 ,则方阵A的特征值是
,则方阵A的特征值是 的根,即
的根,即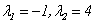 .
.
(6)设 都是方阵A的属于同一特征值
都是方阵A的属于同一特征值 的特征向量,则
的特征向量,则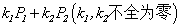 也是
也是 的特征向量.
的特征向量.
(7)属于不同特征值的特征向量线性无关.
(8)属于不同特征值的线性无关的特征向量的并集仍线性无关.
3. 方阵的对角化
(1)若方阵A与对角矩阵Λ相似,则说A可以对角化.即存在可逆矩阵P,使得 .
.
(Λ是以A的n个特征值为对角元素的对角矩阵.)
(2)n阶方阵A可以对角化的充分必要条件是
①A有n个线性无关的特征向量;
②属于每一个特征值的线性无关的特征向量的个数与该特征值的重数相同.
(3)n阶方阵A可以对角化的充分条件是n阶方阵A的n个特征值互不相等.
(4)若A与B相似,则 与
与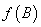 相似.
相似.
4. 实对称矩阵的对角化
(1)实对称矩阵的属于不同特征值的特征向量彼此正交.
(2)实对称矩阵一定可以对角化. 即存在正交矩阵P,使得 .
.
(Λ是以A的n个特征值为对角元素的对角矩阵.)
(3)利用正交矩阵将对称矩阵化为对角矩阵的步骤:
(1)求特征值;(2)求特征向量;(3)将特征向量正交化,单位化;(4)最后将这些特征向量做成矩阵.
二次型
1. 二次型的标准化
(1) 用正交变换化二次型为标准形的具体步骤:
① 写出二次型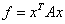 的对称矩阵A;
的对称矩阵A;
② 求A的全部特征值 ;
;
③ 求每个特征值的线性无关的特征向量 ;
;
④ 将特征向量正交化,单位化,得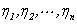 ;
;
⑤ 将这些特征向量做成矩阵,记 ,最后做正交变换x=Cy,得到f的标准形为
,最后做正交变换x=Cy,得到f的标准形为
 .(其中
.(其中 是
是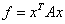 的矩阵A的特征值.)
的矩阵A的特征值.)
(2) 用配方法化二次型为标准形的具体步骤:
① 若二次型含有 的平方项,则先把含有
的平方项,则先把含有 的项集中,然后配方,再对其余的变量同样进行,直到都配成平方项为止,经过可逆的线性变换,就得到标准形;
的项集中,然后配方,再对其余的变量同样进行,直到都配成平方项为止,经过可逆的线性变换,就得到标准形;
② 若二次型中不含有平方项,则先作可逆线性变换,令 ,(k=1,2,…,n,i≠j)
,(k=1,2,…,n,i≠j)
化二次型为含有平方项的二次型,然后再按1中方法配方.
2. 规范二次型
设二次型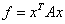 的标准形为
的标准形为 ,(
,( ,r是f的秩)
,r是f的秩)
令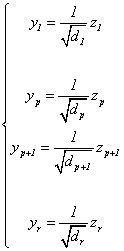 ,得
,得 ,称为二次型
,称为二次型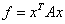 的规范形.
的规范形.
注:规范形是唯一的.其中正平方项的个数p称为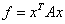 正惯性指数,负平方项的个数r-p称为
正惯性指数,负平方项的个数r-p称为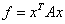 负惯性指数,它们的差p-(r-p)=2p-r称为
负惯性指数,它们的差p-(r-p)=2p-r称为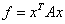 符号差.
符号差.
3. 正定二次型
二次型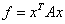 正定
正定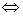 矩阵A正定
矩阵A正定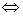 A的特征值全为正
A的特征值全为正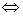 A的各阶顺序主子式都为正.
A的各阶顺序主子式都为正.
二次型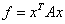 负定
负定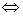 矩阵A负定
矩阵A负定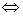 A的奇数阶顺序主子式为负,偶数阶顺序主子式为正.
A的奇数阶顺序主子式为负,偶数阶顺序主子式为正.
-
线性代数知识点总结
《线性代数》复习提纲第二部分:基本知识一、行列式1.行列式的定义用n^2个元素aij组成的记号称为n阶行列式。(1)它表示所有可能…
-
线性代数知识点总结
线性代数知识点总结第一章行列式(一)要点1、二阶、三阶行列式2、全排列和逆序数,奇偶排列(可以不介绍对换及有关定理),n阶行列式的…
-
线性代数知识点总结
线性代数知识点总结第一章行列式(一)要点1、二阶、三阶行列式2、全排列和逆序数,奇偶排列(可以不介绍对换及有关定理),n阶行列式的…
-
线性代数知识点总结
线性代数知识点总结第一章行列式第一节:二阶与三阶行列式把表达式称为所确定的二阶行列式,并记作,即结果为一个数。(课本P1)同理,把…
-
线性代数知识点总结
第一部分基本要求计算方面四阶行列式的计算N阶特殊行列式的计算如有行和列和相等矩阵的运算包括加减数乘乘法转置逆等的混合运算求矩阵的秩…
-
线性代数完美总结版
《线性代数及其应用》一、行列式1、余子式,代数余子式2、几个定理(定理2.2,2.3,2.4)按行展开:A?ai1Ai1?ai2A…
-
线性代数期末复习知识点考点总结
线性代数必考的知识点1、行列式1.n行列式共有n2个元素,展开后有n!项,可分解为2n行列式;2.代数余子式的性质:①、Aij和a…
-
20xx考研真题线性代数试题特点总结
20xx年线性代数依旧是5道考题,两个选择题,一个填空题,两个解答题,两个解答题是22分,今年这两道大题都是常考知识点,并且数学二…
-
线性代数中必考知识点归纳总结
20xx年线性代数必考的知识点1、行列式1.n行列式共有n2个元素,展开后有n!项,可分解为2n行列式;2.代数余子式的性质:①、…
-
线性代数知识点总结
线性代数知识点总结第一章行列式(一)要点1、二阶、三阶行列式2、全排列和逆序数,奇偶排列(可以不介绍对换及有关定理),n阶行列式的…
-
20xx考研真题线性代数试题特点总结
20xx年x月x日来源:跨考教育分享到:新浪微博搜狐微博腾讯微博网易微博人人网20xx年线性代数依旧是5道考题,两个选择题,一个填…