极限计算方法总结
极限计算方法总结
《高等数学》是理工科院校最重要的基础课之一,极限是《高等数学》的重要组成部分。求极限方法众多,非常灵活,给函授学员的学习带来较大困难,而极限学的好坏直接关系到《高等数学》后面内容的学习。下面先对极限概念和一些结果进行总结,然后通过例题给出求极限的各种方法,以便学员更好地掌握这部分知识。
一、极限定义、运算法则和一些结果
1.定义:(各种类型的极限的严格定义参见《高等数学》函授教材,这里不一一叙述)。
说明:(1)一些最简单的数列或函数的极限(极限值可以观察得到)都可以用上面的
极限严格定义证明,例如: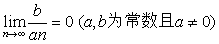 ;
;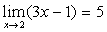 ;
;
 ;等等
;等等
(2)在后面求极限时,(1)中提到的简单极限作为已知结果直接运用,而不需再用极限严格定义证明。
2.极限运算法则
定理1 已知 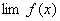 ,
,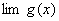 都存在,极限值分别为A,B,则下面极限都存在,且有 (1)
都存在,极限值分别为A,B,则下面极限都存在,且有 (1)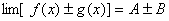
(2)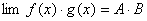
(3)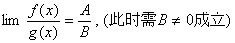
说明:极限号下面的极限过程是一致的;同时注意法则成立的条件,当条件不满足时,不能用。
3.两个重要极限
(1) 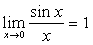
(2) 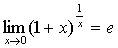 ;
; 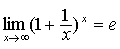
说明:不仅要能够运用这两个重要极限本身,还应能够熟练运用它们的变形形式,
作者简介:靳一东,男,(1964—),副教授。
例如: ,
,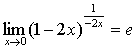 ,
,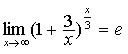 ;等等。
;等等。
4.等价无穷小
定理2 无穷小与有界函数的乘积仍然是无穷小(即极限是0)。
定理3 当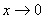 时,下列函数都是无穷小(即极限是0),且相互等价,即有:
时,下列函数都是无穷小(即极限是0),且相互等价,即有:
 ~
~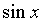 ~
~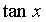 ~
~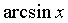 ~
~ ~
~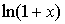 ~
~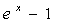 。
。
说明:当上面每个函数中的自变量x换成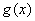 时(
时(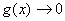 ),仍有上面的等价
),仍有上面的等价
关系成立,例如:当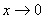 时,
时,  ~
~ 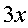 ;
; ~
~  。
。
定理4 如果函数 都是
都是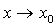 时的无穷小,且
时的无穷小,且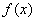 ~
~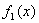 ,
,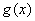 ~
~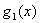 ,则当
,则当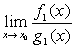 存在时,
存在时, 也存在且等于
也存在且等于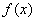
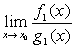 ,即
,即 =
=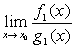 。
。
5.洛比达法则
定理5 假设当自变量x趋近于某一定值(或无穷大)时,函数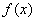 和
和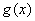 满足:(1)
满足:(1)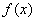 和
和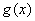 的极限都是0或都是无穷大;
的极限都是0或都是无穷大;
(2)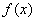 和
和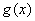 都可导,且
都可导,且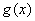 的导数不为0;
的导数不为0;
(3)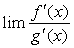 存在(或是无穷大);
存在(或是无穷大);
则极限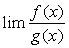 也一定存在,且等于
也一定存在,且等于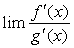 ,即
,即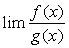 =
=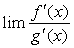 。
。
说明:定理5称为洛比达法则,用该法则求极限时,应注意条件是否满足,只要有一条不满足,洛比达法则就不能应用。特别要注意条件(1)是否满足,即验证所求极限是否为“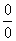 ”型或“
”型或“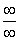 ”型;条件(2)一般都满足,而条件(3)则在求导完毕后可以知道是否满足。另外,洛比达法则可以连续使用,但每次使用之前都需要注意条件。
”型;条件(2)一般都满足,而条件(3)则在求导完毕后可以知道是否满足。另外,洛比达法则可以连续使用,但每次使用之前都需要注意条件。
6.连续性
定理6 一切连续函数在其定义去间内的点处都连续,即如果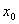 是函数
是函数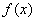 的定义去间内的一点,则有
的定义去间内的一点,则有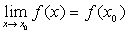 。
。
7.极限存在准则
定理7(准则1) 单调有界数列必有极限。
定理8(准则2) 已知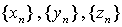 为三个数列,且满足:
为三个数列,且满足:
(1) 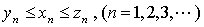
(2) 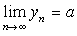 ,
,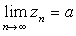
则极限 一定存在,且极限值也是a ,即
一定存在,且极限值也是a ,即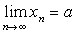 。
。
二、求极限方法举例
1. 用初等方法变形后,再利用极限运算法则求极限
例1 
解:原式= 。
。
注:本题也可以用洛比达法则。
例2 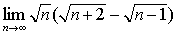
解:原式= 。
。
例3 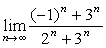
解:原式 。
。
2. 利用函数的连续性(定理6)求极限
例4 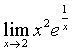
解:因为 是函数
是函数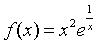 的一个连续点,
的一个连续点,
所以 原式=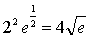 。
。
3. 利用两个重要极限求极限
例5 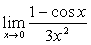
解:原式=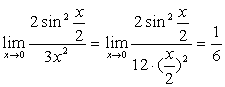 。
。
注:本题也可以用洛比达法则。
例6 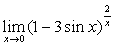
解:原式=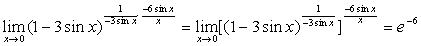 。
。
例7 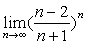
解:原式=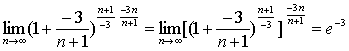 。
。
4. 利用定理2求极限
例8 
解:原式=0 (定理2的结果)。
5. 利用等价无穷小代换(定理4)求极限
例9 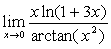
解: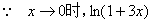 ~
~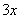 ,
,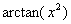 ~
~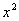 ,
,
 原式=
原式= 。
。
例10 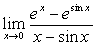
解:原式=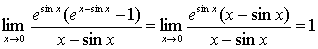 。
。
注:下面的解法是错误的:
原式=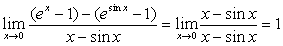 。
。
正如下面例题解法错误一样:
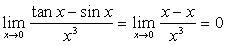 。
。
例11 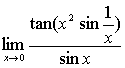
解: ,
,
所以, 原式=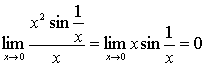 。(最后一步用到定理2)
。(最后一步用到定理2)
6. 利用洛比达法则求极限
说明:当所求极限中的函数比较复杂时,也可能用到前面的重要极限、等价无穷小代换等方法。同时,洛比达法则还可以连续使用。
例12 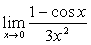 (例4)
(例4)
解:原式=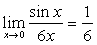 。(最后一步用到了重要极限)
。(最后一步用到了重要极限)
例13 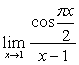
解:原式=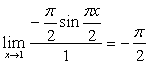 。
。
例14 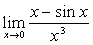
解:原式=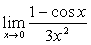 =
=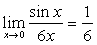 。(连续用洛比达法则,最后用重要极限)
。(连续用洛比达法则,最后用重要极限)
例15 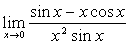
解:
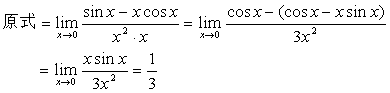
例18 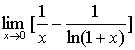
解:错误解法:原式=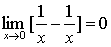 。
。
正确解法:
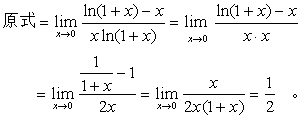
应该注意,洛比达法则并不是总可以用,如下例。
例19 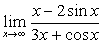
解:易见:该极限是“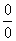 ”型,但用洛比达法则后得到:
”型,但用洛比达法则后得到: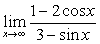 ,此极限
,此极限
不存在,而原来极限却是存在的。正确做法如下:
原式=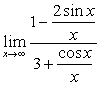 (分子、分母同时除以x)
(分子、分母同时除以x)
=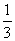 (利用定理1和定理2)
(利用定理1和定理2)
7. 利用极限存在准则求极限
例20 已知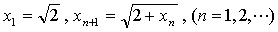 ,求
,求
解:易证:数列 单调递增,且有界(0<
单调递增,且有界(0<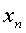 <2),由准则1极限
<2),由准则1极限 存在,设
存在,设 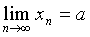 。对已知的递推公式
。对已知的递推公式  两边求极限,得:
两边求极限,得:
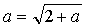 ,解得:
,解得: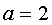 或
或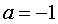 (不合题意,舍去)
(不合题意,舍去)
所以  。
。
例21 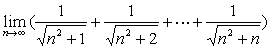
解: 易见: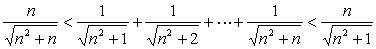
因为  ,
,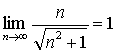
所以由准则2得: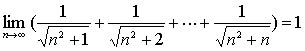 。
。
上面对求极限的常用方法进行了比较全面的总结,由此可以看出,求极限方法灵活多样,而且许多题目不只用到一种方法,因此,要想熟练掌握各种方法,必须多做练习,在练习中体会。另外,求极限还有其它一些方法,如用定积分求极限等,由于不常用,这里不作介绍。
极限与连续的62个典型习题
习题1 设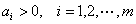 ,求
,求  .
.
解 记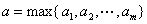 ,则有
,则有
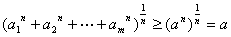 ,
,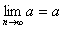 .另一方面
.另一方面
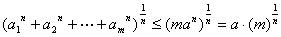 .
.
因为 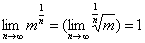 ,故
,故 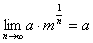 .利用两边夹定理,知
.利用两边夹定理,知
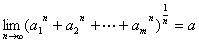 ,其中
,其中 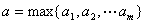 .
.
例如 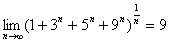 .
.
习题2求  .
.
解

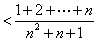 ,
,
即 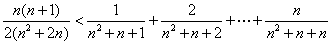
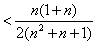
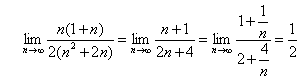 .
.
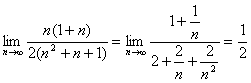 .
.
利用两边夹定理知
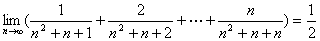 .
.
习题3 求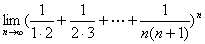 .
.
解 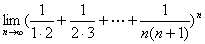
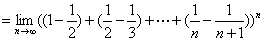
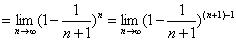


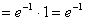
习题4 求 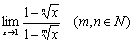 .
.
解(变量替换法)令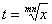 ,则当
,则当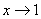 时,
时,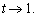 于是,
于是,
原式 .
.
习题5求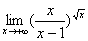 .
.
解(变量替换法)令 ,
,
原式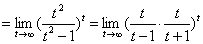
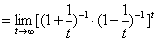
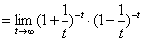
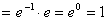 .
.
习题6求  (
(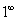 型)。
型)。
为了利用重要极限,对原式变形
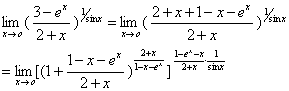
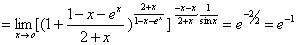
习题7 求 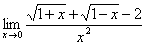 . 解 原式
. 解 原式
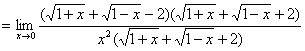
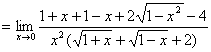


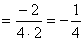 .
.
习题8 求 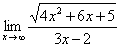 . 解 由于
. 解 由于
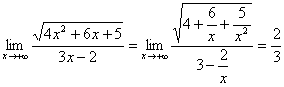 .
.
而

 .故
.故  不存在。
不存在。
习题9 研究下列极限 (1) .
.
∵ 原式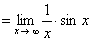 ,其中
,其中 ,
,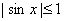 . ∴ 上式极限等于0,即
. ∴ 上式极限等于0,即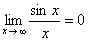 .(2)
.(2)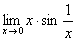 .
.
因为 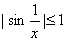 ,
,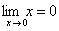 , 所以
, 所以 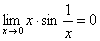 .
.
(3)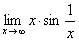 . 原式
. 原式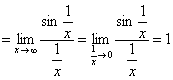 .
.
习题10 计算 .
.
解 原式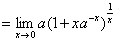

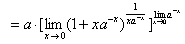
 .
.
习题11 
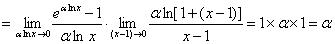 .
.
习题12 已知 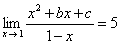 ,求
,求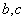 的值。
的值。
解 首先 ,∴
,∴
原式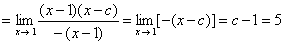 ,
,
∴  ,而
,而 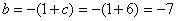 .
.
习题13 下列演算是否正确?
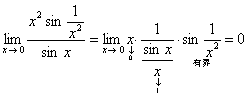 .
.
习题14 求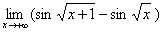 .
.
解 原式
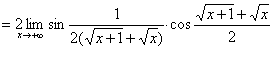
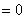 .
.
习题15 求 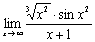 .
.
解 ∵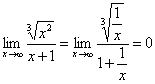 ,
,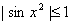 ,原式 = 0.
,原式 = 0.
习题16证明 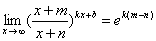 (
( 为常数)。
为常数)。
证 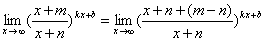 (令
(令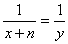 )
)
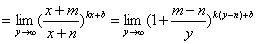
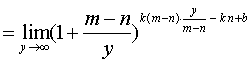


 .
.
习题17 求 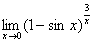 .
.
解 原式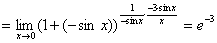 .
.
习题18 求  . 解 (连续性法)
. 解 (连续性法)
原式
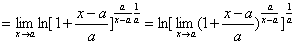
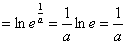 .
.
习题19 试证方程 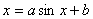 (其中
(其中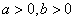 )至少有一个正根,并且它不大于
)至少有一个正根,并且它不大于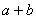 .
.
证 设 ,此初等函数在数轴上连续,
,此初等函数在数轴上连续,
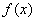 在
在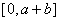 上必连续。∵
上必连续。∵ 而
而
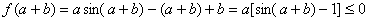 若
若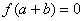 ,则
,则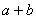 就是方程
就是方程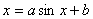 的一个正根。
的一个正根。
若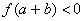 ,则由零点存在定理可知在
,则由零点存在定理可知在 内至少存在一点
内至少存在一点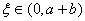 ,使
,使 .即
.即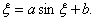
故方程 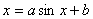 至少有一正根,且不大于
至少有一正根,且不大于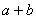 .
.
习题21 求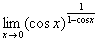 .
.
解 原式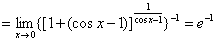 .
.
习题20 设 满足
满足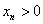 且
且 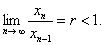 试证
试证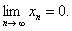
证 
 取
取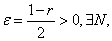 使得当
使得当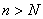 时有
时有
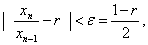 即
即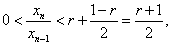 亦即
亦即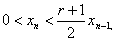 于是递推得
于是递推得 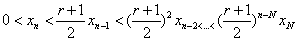
 从而由两边夹准则有
从而由两边夹准则有 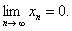
习题22 用定义研究函数 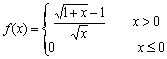 的连续性。
的连续性。
证 首先,当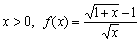 是连续的。同理,当
是连续的。同理,当
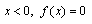 也是连续的。而在分段点
也是连续的。而在分段点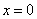 处
处
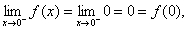

 故
故
习题23 求证 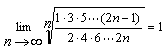 .
.
证 ∵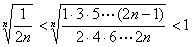 ,而
,而
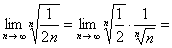
 .由两边夹定理知,原式成立.
.由两边夹定理知,原式成立.
习题24设 任取
任取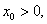 记
记
 试证
试证 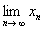 存在,并求极限值。
存在,并求极限值。
证 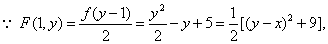
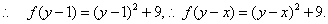 故
故
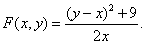 由题设
由题设

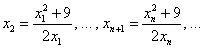 由于
由于
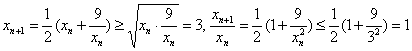
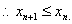 故
故 单调有下界,故有极限。设
单调有下界,故有极限。设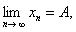
由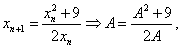 解出
解出 (舍去
(舍去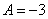 )。
)。
习题25设 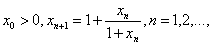 求
求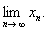
解 显然 有上界
有上界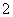 ,有下界
,有下界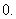
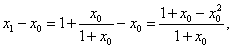 当
当 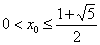 时
时
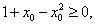 即
即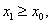 假设
假设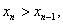 则
则
 故
故 单增。
单增。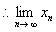
存在。设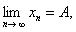 则由
则由 得
得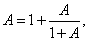 即
即
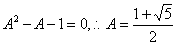 (舍去负值)。当
(舍去负值)。当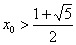 时,有
时,有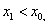
用完全类似的方法可证 单减有下界
单减有下界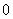 ,同理可证
,同理可证 
习题26设数列 由下式给出
由下式给出 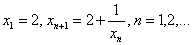 求
求 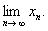
解  不是单调的,但
不是单调的,但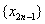 单增,并以3为上界,故有极限。设
单增,并以3为上界,故有极限。设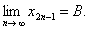
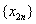 单减,并以2为下界,设
单减,并以2为下界,设 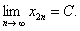 在等式
在等式 两边按奇偶取极限,得两个关系
两边按奇偶取极限,得两个关系 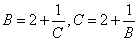 ,解出
,解出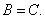 由于的奇数列与偶数列的极限存在且相等,因此
由于的奇数列与偶数列的极限存在且相等,因此 的极限存在,记
的极限存在,记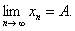 于是
于是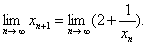 故有
故有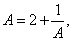 解出
解出 (舍去负值
(舍去负值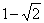 )
)
习题27设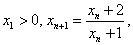
 试证
试证 收敛,并求极限。
收敛,并求极限。
证 显然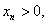 假设
假设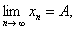 则由
则由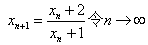 ,可解出
,可解出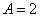 (舍去
(舍去 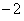 )。下面证明
)。下面证明 收敛于
收敛于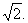 由于
由于
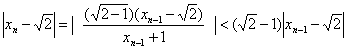 ,
,
递推可得 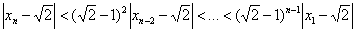
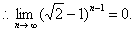 由两边夹可得
由两边夹可得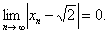 故
故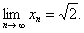
习题28设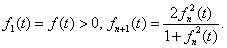 试证
试证
(1)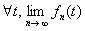 存在;(2)当
存在;(2)当 时,
时,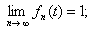 当
当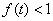 时,
时,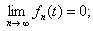
证 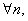 显然有
显然有 又
又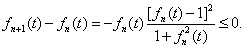
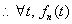 单减有下界。
单减有下界。 收敛。令
收敛。令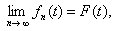 在原式两边取极限得
在原式两边取极限得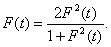 由此可解出
由此可解出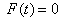 或
或 当
当 时,
时,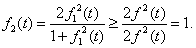 归纳假设
归纳假设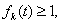 则
则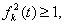 而
而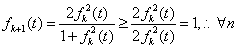 ,有
,有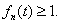 因此
因此 时
时 即
即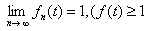 时)。
时)。
当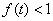 时,由
时,由 的单减性便知即当
的单减性便知即当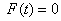 时,即
时,即
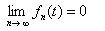 (当
(当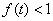 时)。
时)。
习题29 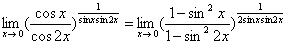
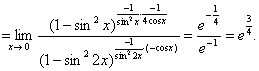
习题30若 收敛,则
收敛,则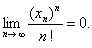
证 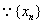 收敛,设
收敛,设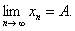 故
故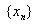 必有界。设
必有界。设
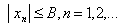 因此
因此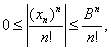 而
而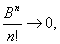

习题31求 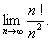
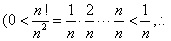
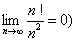
变量替换求极限法
(为求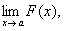 有时可令
有时可令 而
而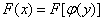 )
)
习题32求 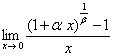 (
(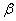 为自然数)
为自然数)
解 令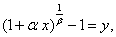 则
则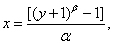 因此
因此
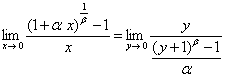
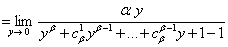
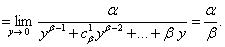
习题33求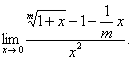
解 令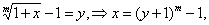 且当
且当 时
时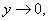 故 原式
故 原式
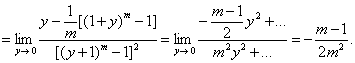
习题34求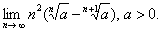
解 先求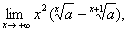 令
令 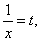 则上式
则上式
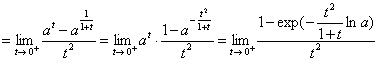
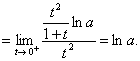 故原式
故原式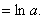
用等价无穷小替换求极限
习题35求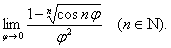
解 记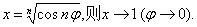
原式=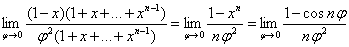
= 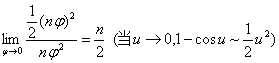
习题36设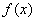 与
与 是等价无穷小,
是等价无穷小,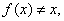 求证
求证
(1)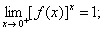 (2)
(2)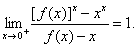
证 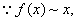 即
即
其中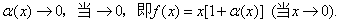 故
故
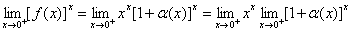
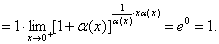
(2)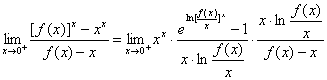
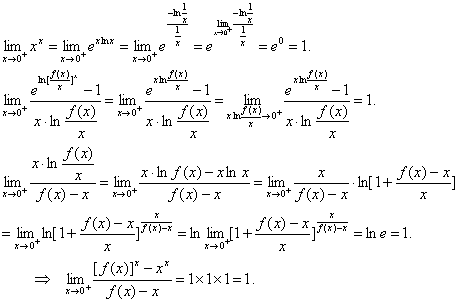
习题37设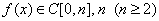 为自然数,
为自然数, 试证
试证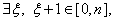 使
使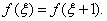
证 (分析:要证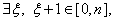 使
使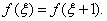 即要证
即要证 有根
有根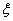 ) 令
) 令 ,显然在
,显然在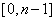 上连续,于是
上连续,于是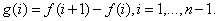 记
记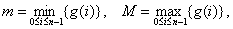 则
则
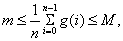 又
又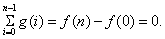 对函数
对函数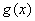 应用介值定理,知
应用介值定理,知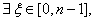 使
使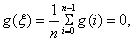 即存在
即存在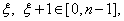 使
使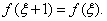
习题38设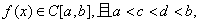 证明
证明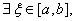
使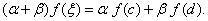
证 (分析:将结果变形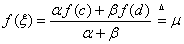 )
)
记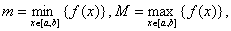 则
则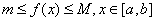
于是 
或 
由介值定理知
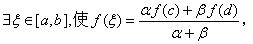 即
即 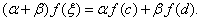
习题39设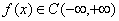 且
且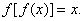 证
证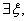 使
使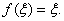
证 反证法。若不存在点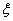 使
使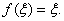 即
即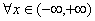 均有
均有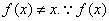 连续,不妨设恒有
连续,不妨设恒有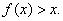 于是
于是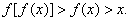 此与
此与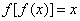 矛盾。故
矛盾。故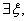 使
使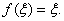
习题40设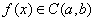 且
且 又
又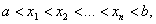 证明至少有一点
证明至少有一点 使
使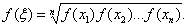
证 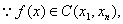 故
故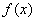 在
在 上有最大值
上有最大值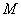 和最小值
和最小值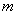 ,使
,使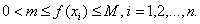 于是
于是 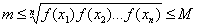 由介值定理,知
由介值定理,知 使
使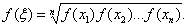
习题41 证明方程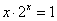 至少有一个小于1的正根。
至少有一个小于1的正根。
证 设 显然
显然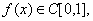 但
但
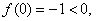
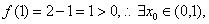 使
使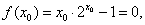 即方程
即方程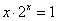 至少有一个小于1的正根
至少有一个小于1的正根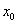 存在。
存在。
习题42 设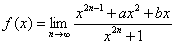 连续,求
连续,求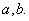
解 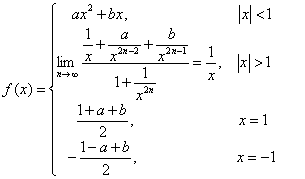
故 由于
由于 在=1,-1处连续,所以
在=1,-1处连续,所以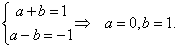
习题43 试证方程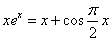 至少有一个实根。
至少有一个实根。
证 做函数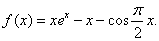 显然
显然
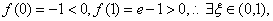 使
使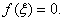 即
即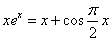 在
在 内必有实根。
内必有实根。
习题44 求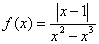 的连续区间。
的连续区间。
(解:先改写为分段函数,结论为: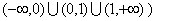
习题45 求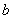 为何值时,函数
为何值时,函数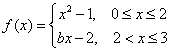 ,在
,在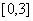 上处处连续。
上处处连续。
只需讨论分段点处的连续性: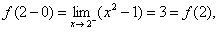
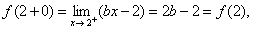 要在
要在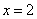 处连续,必有
处连续,必有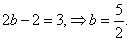
习题46 设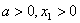 ,定义
,定义 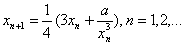 求
求 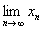
解 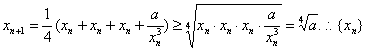 有下界
有下界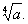 即
即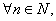 有
有 又
又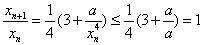 ,即
,即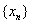 单减有下界,故有极限。设
单减有下界,故有极限。设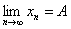 且
且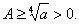 有
有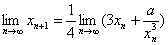 有
有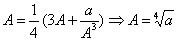
(舍去负根)(注意:先证明极限的存在是必要的。)
习题47
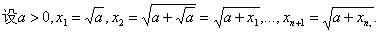
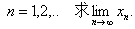
(解: 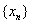 单增有上界
单增有上界 ,可解出极限
,可解出极限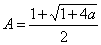 )
)
习题48 设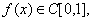 且
且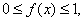 证明
证明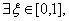 使
使 
证 若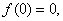 则取
则取 若
若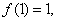 则可取
则可取
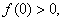
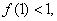 则令
则令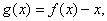 必有
必有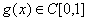 且
且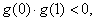 由零点定理知
由零点定理知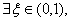 使
使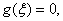 即
即
习题49 (选择题)设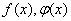 在
在 内有定义,
内有定义, 连续且
连续且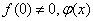 有间断点,则
有间断点,则
(A) 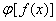 必有间断点,(B)
必有间断点,(B) 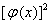 必有间断点,
必有间断点,
(C) 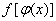 必有间断点,(D)
必有间断点,(D) 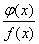 必有间断点.
必有间断点.
解 选[D]((A) 因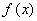 的值域可能很小。
的值域可能很小。
(B)反例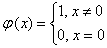 而
而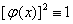 无间断点。
无间断点。
(C) 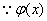 总有定义。
总有定义。
习题50 证明方程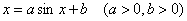 至少有一个正根,且不超过
至少有一个正根,且不超过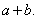
证 设 而
而
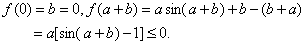
如果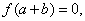 则
则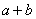 即为
即为 的零点.如果
的零点.如果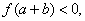 则由介值定理知
则由介值定理知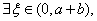 使
使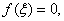 即
即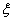 为所求,故原命题成立.
为所求,故原命题成立.
习题51若函数 可以达到最大值和最小值,求证
可以达到最大值和最小值,求证 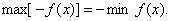
证 设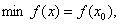 则对任意
则对任意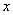 有
有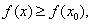 或有
或有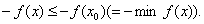 由
由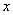 的任意性,可知
的任意性,可知
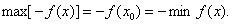
习题52 设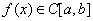 且恒大于零,证明
且恒大于零,证明 在
在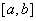 上连续.
上连续.
证 任取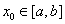 由于
由于 在
在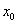 处连续且大于
处连续且大于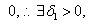 使当
使当 时(若
时(若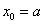 为左端点,则应为
为左端点,则应为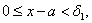 类似处理
类似处理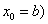 有
有
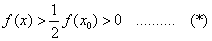
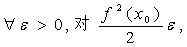 可找到
可找到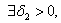 使当
使当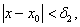 时有
时有 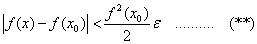
取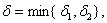 则当
则当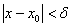 时,有
时,有
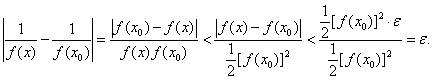
故知 在
在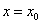 处连续。由
处连续。由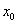 的任意性,知
的任意性,知 在
在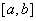 上连续.
上连续.
习题53设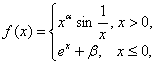 试讨论
试讨论 在
在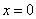 处的连续性.
处的连续性.
解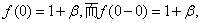

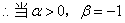 时,
时, 在
在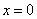 处连续,
处连续,
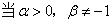 时,
时, 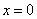 为
为 的跳跃间断点(第一类间断点).当
的跳跃间断点(第一类间断点).当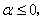 时
时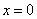 为第二间断点。
为第二间断点。
习题54 设函数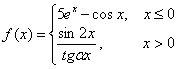 问当
问当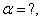
 在
在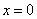 处连续。 解
处连续。 解
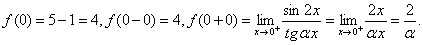
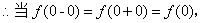 即
即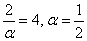 时,
时, 在
在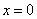 处连续。
处连续。
习题55 求函数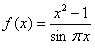 的间断点,并判定其类型.
的间断点,并判定其类型.
解 因当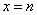 (
(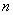 为任一整数)时,
为任一整数)时,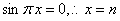 是
是 的间断点。再细分,当
的间断点。再细分,当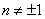 时,
时,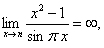 不存在,故除
不存在,故除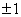 处的任何整数都是
处的任何整数都是 的第二类间断点。因
的第二类间断点。因
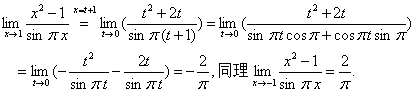
亦即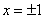 是
是 的第一类(可去)间断点.
的第一类(可去)间断点.
习题56 求函数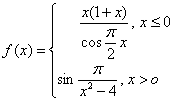 的间断点并判定其类型。
的间断点并判定其类型。
解  的分段点为
的分段点为 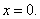
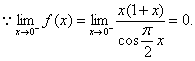
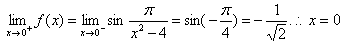 是
是 的第一类(跳跃)间断点。当
的第一类(跳跃)间断点。当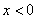 时,
时,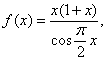 在点
在点
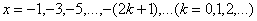 处,
处, 无意义,故
无意义,故 是
是 的间断点。因为
的间断点。因为
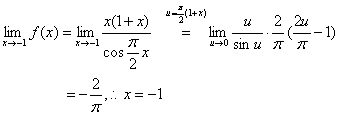
是第一类(可去)间断点。显然 都是极限为
都是极限为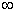 的第二类间断点。当
的第二类间断点。当 时,
时,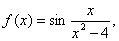 在点
在点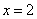 时,
时, 没定义,故
没定义,故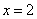 是
是 的间断点。又
的间断点。又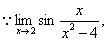 不存在,故为第二类间断点。
不存在,故为第二类间断点。
习题57 设函数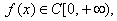 且
且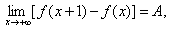 试证
试证 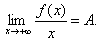
证 因为连续,所以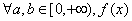 在
在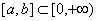 上有界。又因为
上有界。又因为 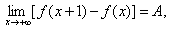 所以
所以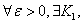
当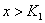 时,恒有
时,恒有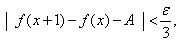 取
取 则存在自然数
则存在自然数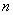 使得
使得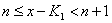 .记
.记 ,则
,则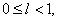 且
且 于是
于是
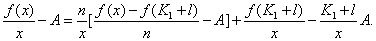 下面估计上式右边三项的绝对值。
下面估计上式右边三项的绝对值。
(1)
 =
=
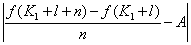
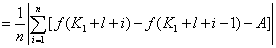
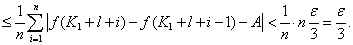
(2)因为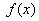 在
在 上有界,即
上有界,即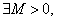 使
使 .故
.故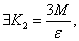 当
当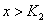 时,恒有
时,恒有 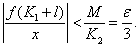
(3)因为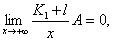 故
故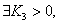 使当
使当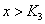 时恒有
时恒有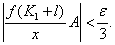 综合(1),(2),(3)
综合(1),(2),(3) 取
取
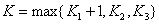 ,则当
,则当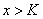 时,恒有
时,恒有
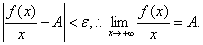
习题68 若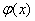 和
和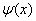 为连续周期函数,当
为连续周期函数,当 时,有定义,且
时,有定义,且 证明
证明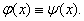
证 先证明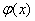 和
和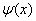 有相同周期。设
有相同周期。设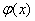 的周期为
的周期为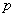 ,则
,则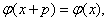 由于当
由于当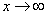 时,
时, 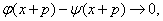 即得
即得  ,以及
,以及
 =
=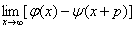
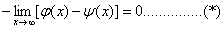
现在说明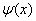 的周期也是
的周期也是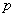 。若不然,则至少存在一个
。若不然,则至少存在一个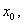 使
使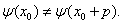 设
设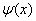 的周期为
的周期为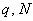 为任意正整数,
为任意正整数,
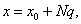 以及
以及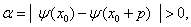 此时恒有
此时恒有
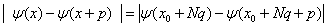
 .
.
但由(*),对充分大的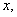 必成立
必成立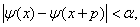 这显然矛盾(矛盾于
这显然矛盾(矛盾于 )
)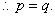 下面证明
下面证明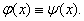 若结论不真,则至少存在一个
若结论不真,则至少存在一个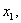 使
使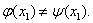 记
记 则
则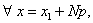 恒有
恒有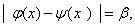 这与
这与 矛盾。于是
矛盾。于是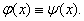

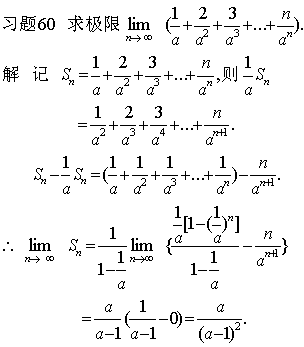
习题61 试证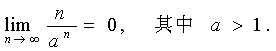

习题62 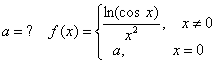 在
在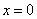 点连续。
点连续。
解
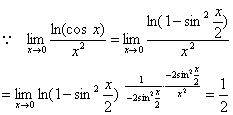
如果函数在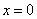 连续,则
连续,则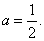
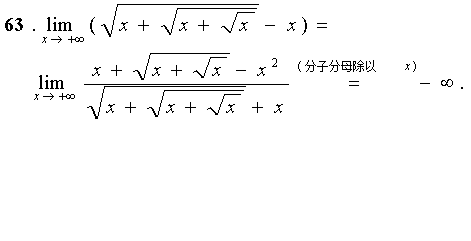
-
极限计算方法总结
极限计算方法总结靳一东高等数学是理工科院校最重要的基础课之一极限是高等数学的重要组成部分求极限方法众多非常灵活给函授学员的学习带来…
-
极限方法总结
首先对极限的总结如下极限的保号性很重要就是说在一定区间内函数的正负与极限一致1极限分为一般极限还有个数列极限区别在于数列极限时发散…
-
求极限的方法总结__小论文
求数列极限的方法总结数学科学学院数学与应用数学08级汉班**指导教师****摘要数列极限的求法一直是数列中一个比较重要的问题,本文…
-
极限计算方法总结
一、极限计算方法总结1.性质:limf(x)?Ax??的充分必要条件是:limx???f(x)?limf(x)?Ax???2.极限…
-
极限计算方法总结
电力电子科学与技术101班高等数学论文极限方法总结20xx10107刘帅20xx10110孙力铎20xx52920xx10113张…
-
求极限方法小结
一.横向总结:1.活用2个重要极限2.a有界函数与无穷小的乘积是无穷小b无穷小与无穷大的关系:无穷大的倒数为无穷小,恒不为零的无穷…
-
高等数学求极限的常用方法(附例题和详解)
高等数学求极限的14种方法一、极限的定义1.极限的保号性很重要:设x?x0limf(x)?,(i)若A?0,则有??0,使得当0?…
-
高等数学B上册 求极限方法总结
求极限的几种常用方法1.约去零因子求极限例1:求极限limx?1x4?1x?1【说明】x?1表明x与1无限接近,但x?1,所以x?…
-
高数求极限的16种方法(超经典)高彦辉总结
L.+'''+.+'''+.+天天快乐+'+..+'+.+爱爱爱爱祝爱爱愿爱爱你爱爱永爱爱远爱爱被爱爱爱爱爱包爱爱围爱爱爱爱爱爱爱…
-
高数:总结求极限的常用方法
总结求极限的常用方法,详细列举,至少4种极限定义法泰勒展开法。洛必达法则。等价无穷小和等价无穷大。极限的求法1.直接代入法适用于分…
-
高等数学中易错知识点总结
1.在一元函数中,若函数在某点连续,则该函数在该点必有极限。若函数在某点不连续,则该函数在该点必无极限。2,在一元函数中,若函数在…