数据结构实验报告 二叉树
实验报告
实验目的:
1. 掌握树及二叉树的基本概念;
2. 掌握二叉树的存储结构;
3. 掌握二叉树的遍历。
实验内容:
算术表达式与二叉树之间存在着对应关系,编写一算法将前缀形式输入的算术表达式按中缀方式输出。
实验原理:
根据访问二叉树根节点的顺序,可以分为先序遍历、中序遍历、后序遍历。算术表达式与二叉树之间存在着对应的关系。在本程序建立的二叉树中,先序遍历输出的结果将是前缀表达式,中序遍历输出的结果将是中缀表达式。按照某种既定的规则建立二叉树,然后输出。 设计思想:
本程序定义了结点类、二叉树类。在结点类中定义了构造函数,二叉树类中定义了构造函数、建立二叉树函数、中序遍历函数。
在前缀表达式中,很容易将最后两个数据混为一谈。在本程序中,在输入时要求输入后的每个数据以#结尾,这样既避免了两个数据混为一谈,同时结束了该子树的建立,方便了二叉树的建立。
建立二叉树函数中,如果输入的是运算符号,则递归调用建立函数分别建立左子树和右子树;如果输入的是数字,则递归调用建立函数建立右子树;如果输入的是#,则该节点为空,结束递归调用。反复的递归调用,直至二叉树建成为止。然后按照中序遍历输出即可。 实现部分:
源代码:
#include<iostream.h>
class btree;
class bintreenode
{friend class btree;
char data;
bintreenode *lchild;
bintreenode *rchild;
public:
bintreenode(){lchild=rchild=NULL;}
bintreenode(char item)
{data=item;
lchild=rchild=NULL;
}
bintreenode(char value,bintreenode *left,bintreenode *right);
};
class btree
{public:
btree(){root=NULL;}
btree(char value,bintreenode *left,bintreenode *right); void creat(bintreenode *&root);
void inorder(bintreenode *root);
protected:
bintreenode *root;
};
//中序遍历函数
void btree::inorder(bintreenode *root)
{if(root!=NULL)
{inorder(root->lchild);
cout<<root->data;
inorder(root->rchild);}
}
//建立二叉树函数
void btree::creat(bintreenode *&root)
{char ch;
cin>>ch;
if(ch=='#') root=NULL;
if(ch=='+'||ch=='-'||ch=='*'||ch=='/')
{
root=new bintreenode;
root->data=ch;
creat(root->lchild);
creat(root->rchild);
}
if(ch>='0'&&ch<='9')
{
root=new bintreenode;
root->data=ch;
creat(root->rchild);
}
}
int main()
{btree bt;
bintreenode *root;
cout<<"请输入前缀表达式,每个数字以#结束:"<<endl; bt.creat(root);
cout<<"转化后的中缀表达式为:"<<endl;
bt.inorder(root);
cout<<endl;
return 0;}
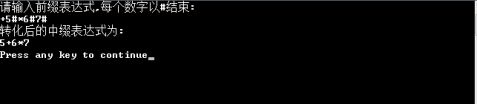
测试用例1.
前缀表达式:+ 5 *6 7
输入前缀表达式:+5#*6#7#
程序运行结果:
2.
前缀表达式:+ 123 * 56 +5 68
输入前缀表达式:+123#*56#+5#68#
程序运行结果:

实验小节:
本程序中,通过#结束子树的建立,同时避免了数据间的混淆,一举两得。 二叉树的建立和遍历的过程中,都是用了递归操作,加深了对递归的认识。
通过本程序的练习,更好的理解了二叉树的基本概念,对二叉树的建立、遍历等基本操作有了更深的认识。
第二篇:二叉树递归遍历 数据结构实验报告
南昌航空大学实验报告
课程名称: 数据结构 实验名称: 实验六 二叉树的递归遍历及其应用 班 级: 学生姓名: 学号: 指导教师评定: 签 名:
题目:假设二叉树采用二叉链表结构。设计并实现如下算法:先序递归建树,
中序非递归遍历该树,输出各个结点的值,并求该树中单分支结点的个数。
一、 需求分析
1. 用户可以根据自己的需求分别输入任意的一个二叉树,并且能够实现中序非递归遍历该
树输出各个结点的数值。
2. 通过已有的二叉树能够求出该树的单分支结点的个数。
3. 程序执行的命令包括:
(1)构造二叉树T (2)遍历二叉树 (3)求二叉树单分支结点的个数
(4)求二叉树的总结点数
二、概要设计
⒈ 为实现上述算法,需要链表的抽象数据类型:
ADT Binarytree {
数据对象:D是具有相同特性的数据元素的集合
数据关系R:
若D为空集,则R为空集,称binarytree为空二叉树;
若D不为空集,则R为{H},H是如下二元关系;
(1) 在D中存在唯一的称为根的数据元素root,它在关系H下无前驱;
(2) 若D-{root}不为空,则存在D-{root}={D1,Dr},且D1∩Dr为空集;
(3) 若D1不为空,则D1中存在唯一的元素x1,<root,x1>∈H,且存在D1
上的关系H1是H的子集;若Dr不为空集,则Dr中存在唯一的元素Xr,
<root,Xr>∈H,且存在Dr上的关系Hr为H的子集;H={<root,x1>,<root,
Xr>,H1,Hr};
(4) (D1,{H1})是一颗符合本定义的二叉树,称为根的左子树,(Dr,{Hr})是一
颗符合本定义的二叉树,称为根的右子树。
基本操作:
Creatbitree(&S,definition)
初始条件:definition给出二叉树S的定义
操作结果:按definition构造二叉树S
counter(T)
初始条件:二叉树T已经存在
操作结果:返回二叉树的总的结点数
onecount(T)
1
初始条件:二叉树T已经存在
操作结果:返回二叉树单分支的节点数
Clearbintree(S)
初始条件:二叉树S已经存在
操作结果:将二叉树S清为空树
Bitreeempty(S)
初始条件:二叉树S已经存在
操作结果:若S为空二叉树,则返回TRUE,否则返回FALSE
Bitreedepth(S,&e)
初始条件:二叉树S已经存在
操作结果:返回S的深度
Parent(S)
初始条件:二叉树S已经存在,e是S中的某个结点
操作结果:若e是T的非根结点,则返回它的双亲,否则返回空 Preordertraverse(S)
初始条件:二叉树S已经存在,Visit是对结点操作的应用函数。 操作结果:先序遍历S,对每个结点调用函数visit一次且仅一次。
一旦visit失败,则操作失败。
Inordertraverse (S,&e)
初始条件:二叉树S已经存在,Visit是对结点操作的应用函数。 操作结果:中序遍历S,对每个结点调用函数visit一次且仅一次。
一旦visit失败,则操作失败。
Postordertraverse (&S,e)
初始条件:二叉树S已经存在,Visit是对结点操作的应用函数。 操作结果:后序遍历S,对每个结点调用函数visit一次且仅一次。
一旦visit失败,则操作失败。
}ADT Binarytree
2. 本程序有三个模块:
⑴ 主程序模块
main(){
初始化;
{
接受命令;
显示结果;
}
}
⑵ 先序建树的模块:主要建立一棵二叉树;
⑶中序遍历模块:输出中序遍历的结果;
(4)单分支结点数模块:输出单分支的结点数。
三、详细设计
⒈元素类型,结点类型
2
/*定义二叉树*/
typedef struct bitnode
{ char data;
struct bitnode *lchild,*rchild;
}bitnode;
/*定义栈元素的类型*/
typedef struct node
{ struct bitnode *p;
}node;
/*定义栈*/
typedef struct stack
{ node *base;
node *top;
int size;
}stack;
2.对抽象数据类型中的部分基本操作的伪码算法如下:
stack *initstack() /*构建空栈*/
{ s->base=(struct node *)malloc(MAX*sizeof(node));
if(!s->base) exit(0);
s->top=s->base;
s->size=MAX;
return s;
}
/*判断栈是否为空栈*/
int stackempty(stack *s)
{ if(s->top==s->base) return 1;
else return 0;
}
/*入栈*/
stack *push(stack *s,struct bitnode *t)
{ if(s->top-s->base==s->size)
{ s->base=(struct node *)realloc(s->base,(s->size+10)*sizeof(node)); if(!s->base) exit(0);
s->top=s->base+s->size;
s->size+=10;
}
(*s->top).p=t;
s->top++;
return s;
}
/*出栈*/
struct bitnode *pop(stack *s)
{ if(s->top==s->base)
3
{ printf("这是一个空栈\n");
return 0;
}
else
{ s->top--;
return ((*s->top).p);
}
}
/*取栈顶的元素*/
struct bitnode *getpop(stack *s)
{ if(s->top==s->base)
{ printf("这是一个的空栈!\n");
return NULL;
}
else return (*(s->top-1)).p;
}
/*先序递归构建二叉树*/
struct bitnode *creatbitree(struct bitnode *r) { char a;
scanf("%c",&a);
if(a==' ') return r=NULL;
else
{ r=(struct bitnode*)malloc(sizeof(bitnode)); r->data=a;
r->lchild=creatbitree(r->lchild);
r->rchild=creatbitree(r->rchild);
} return r;
}
/*中序非递归遍历二叉树*/
void inorder(struct bitnode *T)
{ struct bitnode *p,*q;
p=T;
s=initstack();
if(p)
{ while(p)
{ push(s,p);
p=p->lchild;
}
while(!stackempty(s))
{ p=pop(s);
visit(p->data);
if(p->rchild!=NULL)
{ q=p->rchild;
while(q)
4
{ push(s,q);
q=q->lchild;
}
}
}
}
}
/*求二叉树的结点总数*/
int counter(struct bitnode *T)
{ int num1,num2,num;
if(T==NULL) return 0;
else
{ num1=counter(T->lchild);
num2=counter(T->rchild);
num=num1+num2+1;
return num;
}
}
/*求二叉树的单分支的结点数*/
int onecount(struct bitnode *T)
{ int s1,s2;
if(T==NULL) return(0);
else
{ s1=onecount(T->lchild);
s2=onecount(T->rchild);
if((T->lchild!=NULL&&T->rchild==NULL)||(T->rchild!=NULL&&T->lchild==NULL)) return (s1+s2+1);
else return (s1+s2);
}
}
3.主函数和其他函数的伪码算法
main()
{ int sum;
printf("xian xu shu ru bitree:\n");
T=creatbitree(T); /*创建二叉树*/
a=counter(T); /*求结点总数*/
printf("\na=%d\n",a);
printf("\nxian xu bian li bitree:\n");
inorder(T); /*中序遍历二叉树*/
sum=onecount(T); /*求单分支的结点数*/
printf("\n\nthe bitree dan fen zhi jie dian shu:\nSUM=%d\n",sum);
getch();
}
/*访问元素*/
5
void visit(char ch)
{ if(i!=(a-1))
{ printf("%c->",ch);
i++;
}
else
{ printf("%c",ch);
printf("\n");
}
}
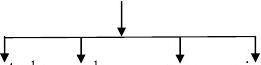
4 函数调用关系

四、调试分析
⒈初步完成编程的工作时,在输入二叉树的发现只能输入一个字符,而且程序不再进行,最
后是自己的不小心将语句char a; scanf("%c",&a);中的%c写为%d导致的。
⒉ 在编写元素入栈和出栈的时候,程序报如下的错误:语法有错误。提示语句return
((*s->top).p);有错,经过检查原来是定义的时候的类型使用错了。
3.在编译的时候还有警告的提示:“exp6.c 50:指针转换后指向其它类型在push函数中”,在检查该语句的发现是s->base=(struct node *)realloc(s->base,(s->size+10)
*sizeof(node));中的node写成了二叉树的类型bitnode了,因此出现上述的提示。
4. 算法的时空分析
各操作的算法时间复杂度比较合理
initstack,stackempty,push,pop,getpop,visit为O(1); creatbitree,inorder,
counter,onecount为O(n),
注:n为二叉树的总结点数。
5.本次实验采用数据抽象的程序设计方法,将程序化为三层次结构,设计时思路清晰,使
调试也较顺利,各模块有较好的可重用性。
五、用户手册
⒈ 本程序的运行环境为windows xp操作系统,并且在TC2.0中运行,执行文件为Exp6.c; ⒉.在输入二叉树的时候空格表示为空,输入注意空格的个数;
3. 进入演示程序后,完成编译,再点击超级工具集里的中文DOS环境运行选项,进入DOS
环境中,用户根据需求键入相应的数据,可以看到相应的结果。
六、测试结果
6
所以在wintc中运行得到的结果如下图所示
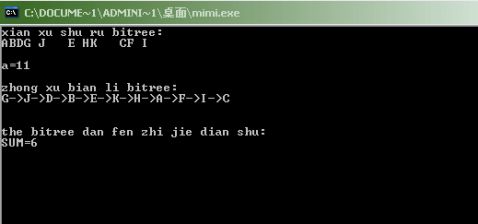
:我输入的二叉树是ABDG J E HK CF I A
运行的结果是: 结点的总数是

11
遍历的结果GJDBEKHAFIC B C
单分支的结点数是6 七、附录:源程序 #include <malloc.h>
#define NULL 0
#define MAX 100
/*定义二叉树*/
typedef struct bitnode
{ char data;
struct bitnode *lchild,*rchild;
}bitnode;
/*定义栈元素的类型*/
typedef struct node
{ struct bitnode *p;
}node;
/*定义栈*/
typedef struct stack
{ node *base;
node *top;
int size;
}stack;
/*全局变量*/
struct bitnode *T;
stack *s;
int i=0,a; /*a为二叉树的结点总数;i为访问结点时的计数*/
/*构建空栈*/
stack *initstack()
{
7
s->base=(struct node *)malloc(MAX*sizeof(node));
if(!s->base) exit(0);
s->top=s->base;
s->size=MAX;
return s;
}
/*判断栈是否为空栈*/
int stackempty(stack *s)
{ if(s->top==s->base) return 1;
else return 0;
}
/*入栈*/
stack *push(stack *s,struct bitnode *t)
{ if(s->top-s->base==s->size)
{
s->base=(struct node *)realloc(s->base,(s->size+10)*sizeof(node)); if(!s->base) exit(0);
s->top=s->base+s->size;
s->size+=10;
}
(*s->top).p=t;
s->top++;
return s;
}
/*出栈*/
struct bitnode *pop(stack *s)
{
if(s->top==s->base)
{ printf("这是一个空栈\n");
return 0;
}
else
{
s->top--;
return ((*s->top).p);
}
}
/*取栈顶的元素*/
struct bitnode *getpop(stack *s)
{
if(s->top==s->base)
{
printf("这是一个的空栈!\n");
return NULL;
8
}
else
return (*(s->top-1)).p;
}
/*先序递归构建二叉树*/
struct bitnode *creatbitree(struct bitnode *r) {
char a;
scanf("%c",&a);
if(a==' ') return r=NULL;
else
{ r=(struct bitnode*)malloc(sizeof(bitnode)); r->data=a;
r->lchild=creatbitree(r->lchild);
r->rchild=creatbitree(r->rchild);
}
return r;
}
/*访问元素*/
void visit(char ch)
{ if(i!=(a-1))
{ printf("%c->",ch);
i++;
}
else
{ printf("%c",ch);
printf("\n");
}
}
/*中序非递归遍历二叉树*/
void inorder(struct bitnode *T)
{ struct bitnode *p,*q;
p=T;
s=initstack();
if(p)
{ while(p)
{ push(s,p);
p=p->lchild;
}
while(!stackempty(s))
{ p=pop(s);
visit(p->data);
if(p->rchild!=NULL)
{ q=p->rchild;
9
while(q)
{ push(s,q);
q=q->lchild;
}
}
}
}
}
/*求二叉树的结点总数*/
int counter(struct bitnode *T)
{ int num1,num2,num;
if(T==NULL) return 0;
else
{ num1=counter(T->lchild);
num2=counter(T->rchild);
num=num1+num2+1;
return num;
}
}
/*求二叉树的单分支的结点数*/
int onecount(struct bitnode *T)
{ int s1,s2;
if(T==NULL) return(0);
else
{ s1=onecount(T->lchild);
s2=onecount(T->rchild);
if((T->lchild!=NULL&&T->rchild==NULL)||(T->rchild!=NULL&&T->lchild==NULL)) return (s1+s2+1);
else return (s1+s2);
}
}
/*主函数*/
main()
{ int sum;
printf("xian xu shu ru bitree:\n");
T=creatbitree(T); /*创建二叉树*/
a=counter(T); /*求结点总数*/
printf("\na=%d\n",a);
printf("\nzhong xu bian li bitree:\n");
inorder(T); /*中序遍历二叉树*/
sum=onecount(T); /*求单分支的结点数*/
printf("\n\nthe bitree dan fen zhi jie dian shu:\nSUM=%d\n",sum);
getch();
}
10
-
数据结构二叉树实验报告
实验三二叉树的遍历一实验目的熟悉二叉树的结点类型和二叉树的基本操作掌握二叉树的前序中序和后序遍历的算法3加深对二叉树的理解逐步培养…
-
数据结构C二叉树实验报告
北京林业大学12学年13学年第1学期数据结构实验报告书专业自动化班级111姓名宁友菊学号111044120实验地点B2机房任课教师…
- 数据结构树和二叉树实验报告
-
数据结构二叉树实验报告(附代码)
一实验构思Conceive10本部分应包括描述实验实现的基本思路包括所用到的离散数学工程数学程序设计算法等相关知识首先构造二叉树的…
-
数据结构二叉树操作实验报告
实验报告指导教师XX实验时间20xx年11月1日学院计算机学院专业信息安全班级XXXXXX学号XXXXX姓名XX实验室S331实验…
-
数据结构二叉树实验报告
实验三二叉树的遍历一实验目的熟悉二叉树的结点类型和二叉树的基本操作掌握二叉树的前序中序和后序遍历的算法3加深对二叉树的理解逐步培养…
-
数据结构_实验9_二叉树遍历的应用
实验报告实验课程数据结构实验项目实验九二叉树遍历的应用实验地点指导教师班级学生姓名金轶洲学号09020xx03教师评分日期浙江传媒…
-
中南民族大学信管二叉树_数据结构实验报告
中南民族大学管理学院学生实验报告实验项目二叉树的建立与遍历课程名称数据结构年级20xx专业信息管理与信息系统指导教师实验地点管理学…
-
数据结构C二叉树实验报告
北京林业大学12学年13学年第1学期数据结构实验报告书专业自动化班级111姓名宁友菊学号111044120实验地点B2机房任课教师…
-
数据结构实验报告——中序遍历二叉树
班级380911班学号57000211姓名徐敏实验报告一实验目的掌握二叉树的链式存储结构掌握构造二叉树的方法加深对二叉树的中序遍历…
-
二叉树实验报告
算法与数据结构实验报告——二叉树课程名称:算法与数据结构实验项目名称:满二叉树的建立与遍历实验时间:20xx年x月x日班级:电科1…