专题3:函数的图象变换总结
专题三:函数的图象变换
一.平移变换:
(1)函数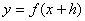
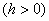 的图象是把
的图象是把 的图象向左平移
的图象向左平移 个单位得到的;
个单位得到的;
(2)函数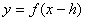
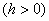 的图象是把
的图象是把 的图象向右平移
的图象向右平移 个单位得到的;
个单位得到的;
(3)函数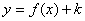
 的图象是把
的图象是把 的图象向上平移
的图象向上平移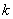 个单位得到的;
个单位得到的;
(4)函数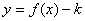
 的图象是把
的图象是把 的图象向下平移
的图象向下平移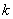 个单位得到的.
个单位得到的.
练习:1.将下列变换的结果填在横线上:
(1)将函数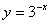 的图象向右平移2个单位,得到函数 的图象;
的图象向右平移2个单位,得到函数 的图象;
(2)将函数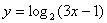 的图象向左平移2个单位,得到函数 的图象.
的图象向左平移2个单位,得到函数 的图象.
2.函数 的图象,可由
的图象,可由 的图象经过下述变换得到( )
的图象经过下述变换得到( )
A.向左平移6个单位 B.向右平移6个单位
C.向左平移3个单位 D.向右平移3个单位
3.讨论函数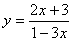 的图像是由哪个反比例函数的图像通过哪些变换而得到?
的图像是由哪个反比例函数的图像通过哪些变换而得到?
二.对称变换
1.同一函数的对称性(自对称)若函数 对定义域内一切
对定义域内一切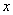
(1)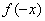 =
=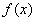
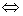 函数
函数 图象关于
图象关于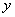 轴对称;
轴对称;
(2)函数 的不可能关于
的不可能关于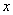 轴对称(除
轴对称(除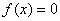 外);
外);
(3)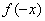 =-
=-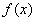
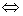 函数
函数 图象关于原点对称;
图象关于原点对称;
(4)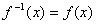
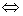 函数
函数 图象关于直线
图象关于直线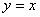 对称;
对称;
(5)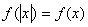
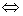 函数
函数 图象关于直线
图象关于直线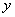 轴对称;
轴对称;
(以下选讲)
(6)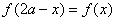
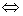 函数
函数 图象关于直线
图象关于直线 对称;
对称;
(7)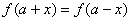
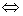 函数
函数 图象关于直线
图象关于直线 对称;
对称;
2.不同函数对称性(互对称)给出函数
(1)函数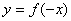 与
与 的图象关于
的图象关于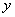 轴对称;
轴对称;
(2)函数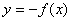 与
与 的图象关于
的图象关于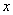 轴对称;
轴对称;
(3)函数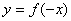 与
与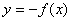 的图象关于原点对称;
的图象关于原点对称;
(4)函数 与
与 的图象关于直线
的图象关于直线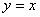 对称;
对称;
三.训练题目
1.已知函数 的定义域为
的定义域为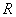 ,则下列说法中:
,则下列说法中:
① 若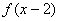 是偶函数,则函数
是偶函数,则函数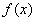 的图象关于直线
的图象关于直线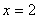 对称;
对称;
② 若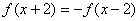 ,则函数
,则函数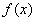 的图象关于原点对称;
的图象关于原点对称;
③ 函数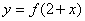 与函数
与函数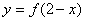 的图象关于直线
的图象关于直线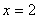 对称;
对称;
④ 函数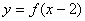 与函数
与函数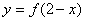 的图象关于直线
的图象关于直线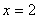 对称.
对称.
其中正确是 .
2.已知函数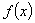 是定义域为
是定义域为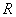 的偶函数,且
的偶函数,且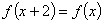 .若
.若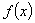 在
在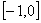 上是减函数,则
上是减函数,则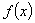 在
在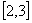 上是( )
上是( )
A.增函数 B.减函数 C.先增后减的函数 D.先减后增的函数
3.函数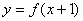 与
与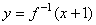 的图像关于( )对称
的图像关于( )对称
A.直线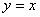 B.直线
B.直线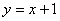 C.直线
C.直线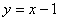 D.直线
D.直线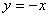
4.设定义域为R的函数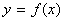 、
、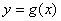 都有反函数,并且
都有反函数,并且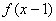 和
和 的函数图像关于直线
的函数图像关于直线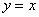 对称,若
对称,若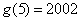 ,那么
,那么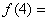 ( )
( )
A. 2002 B. 20## C.2004 D.2005
5.已知函数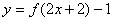 是定义在
是定义在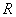 上的奇函数,函数
上的奇函数,函数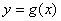 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,若
对称,若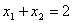 ,则
,则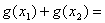 ( )
( )
A.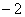 B.
B.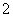 C.
C.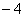 D.
D.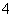
6.已知函数 满足:①
满足:①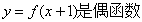 ;②在
;②在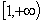 上为增函数.若
上为增函数.若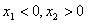 ,且
,且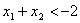 ,则
,则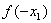 与
与 的大小关系是( )
的大小关系是( )
A. B.
B.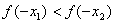
C.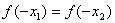 D.不能确定
D.不能确定
7.函数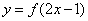 是偶函数,则函数
是偶函数,则函数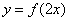 的对称轴是 .
的对称轴是 .
8.设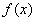 是定义在
是定义在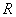 上的偶函数,且
上的偶函数,且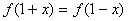 ,当
,当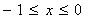 时,
时,
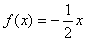 ,则
,则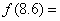 _ _.
_ _.
9.设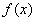 是定义在
是定义在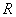 上的奇函数,且图象关于直线
上的奇函数,且图象关于直线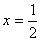 ,则
,则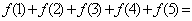 __ ___.
__ ___.
10.函数 对一切实数x都满足
对一切实数x都满足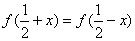 并且方程
并且方程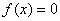 有三个实根,这三个实根的和 .
有三个实根,这三个实根的和 .
11.若函数 的图象关于直线
的图象关于直线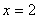 对称,当
对称,当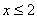 时,
时,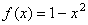 ,则当
,则当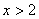 时,则
时,则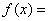 .
.
第二篇:函数专题 精心总结
函数专题
高中函数考察的题型大致是三大类:抽象函数、分段函数、导函数。
考察的内容:函数的解析式与定义域;函数的值域与最值;函数的单调性、奇偶性、周期性、对称性;函数的图形结合。
一、单调性。
①抽象函数的单调性
对于抽象函数的单调性的判断仍然要紧扣单调性的定义,结合题目中所给性质和相应的条件,对任意X1,X2在所给区间内,比较f(X1)-f(X2)与0的大小,或f(X1)/f(X
2)与1的大于。
有时根据需要,需做适当的变形,如X1=X2*(X1/X2)或X1=X2+X1-X2。
1、函数f(x)的定义域为(0,+∞),若在其定义域内恒有f(x)>0,f(ab)=f(a)f(b)。已知当x>1时,f(x)>1,证明f(x)在其定义域上为增函数。 证明:
不妨令b>1,那么由题意可得
f(ab)/f(a)=f(b)>1
即f(ab)>f(a)
又ab>a是显然成立的
由此可推知f(x)为增函数
2、函数f(x)对任意的a,b∈R,都有f(a+b)=f(a)+f(b)-1,并且当x>0时,f(x)>1.
求证:f(x)是R上的增函数.
证明:设X1,X2∈R,且X1<X2,则X2-X1>0,
∴f(X2-X1)>1
f(X2)-f(X1)=f[(X2-X1)+X1]-f(X1)=f(X2-X1)+f(X1)-1-f(X1)=f(X2-X1)-1>0 ∴f(X1)<f(X2)
∴f(X)是R上的增函数
一点有用的东西:
①两个增(减)函数的和仍为增(减)函数,一个增(减)函数与一个减(增)函数的差是增(减)函数。
②奇函数在对称的两个区间上有相同的单调性,偶函数在对称的两个区间上有相反的单调性。
③互为反函数的两个函数有相同的单调性。(很重要)
④如果y=f(u)和u=g(x)的单调性相同,那么y=f[g(x)]是增函数,如果y=f(u)和u=g(x)单调性相反,那么y=f[g(x)]是减函数。 复合函数的单调性
复合函数单调性的判断根据是:设y=f(u),u=g(x),x∈[a,b],u∈[m,n]都是单调函数,则y=f[g(x)]在[a,b]上也是单调函数.
Ⅰ若y=f(u)是[m,n]上的增函数,则y=f[g(x)]的增减性与u=g(x)的增减性相同; Ⅱ若y=f(u)是[m,n]上的减函数,则y=f[g(x)]的增减性与u=g(x)的增减性相反.
复合函数y=f[g(x)]的单调性规律为“同增异减”,即f(x)与g(x)若具有相同的单调性,则f[g(x)]必为增函数;若两者单调性不同则f[g(x)]必为减函数。求复合函数的单调性的步骤为: ①求复合函数的定义域
②把复合函数分解为基本函数
③把中间变量的变化范围转化成自变量的变化范围
④由复合函数的单调性规律判断其单调性或单调区间
是否存在实数a,使函数f(x)=log下标(a)上标(ax^2-x)在区间[2,4]上是增函数?如果存在,说明a可取那些值;如果不存在,请说明理由。
设g(x)=ax^2-x,假设复合条件的a值存在.
当a>1时,为使函数y=f(x)=log(a)&(ax^2-x)在区间[2,4]上是增函数,只需g(x)=ax^2-x在[2,4]上是增函数,故应满足
x=1/2a≤2,g(2)=4a-2>0
解得a>1/2,又a>1,∴a>1
当0<a<1时,为使函数y=f(x)=log(a)&(ax^2-x)在区间[2,4]上是增函数,只需g(x)=ax^2-x在[2,4]上是减函数,故
x=1/2a≥4,g(4)=16a-4>0
无解.
综上可知,当a∈(1,+∞)时,f(x)在[2,4]是增函数
二、奇偶性(注意:在判断一个函数为奇函数或偶函数只前,必须先确定其定义域是否关于原点对称)
①若函数f(x)满足f(-x)/f(x)=1,则其为偶函数;满足f(-x)/f(x)=-1,则其为奇函数. ②奇±奇=奇,偶±偶=偶,
奇×奇=偶,偶×偶=偶,
奇×偶=奇.
③任意一个定义域关于原点对称的函数f(x)均可写成一个奇函数g(X)与一个偶函数h(x)和的形式,即g(x)=[f(x)-f(-x)]/2,h(x)=[f(x)+f(-x)]/2.(很重要)
④若函数y=f(x)是奇函数且0是定义域内的值,则f(0)=0.
第三点如:已知f(x)=…,若f(x)由一个奇函数g(x)和一个偶函数h(x)构成,求g(x)和h(x)的解析表达式。
已知f(x)是R上的奇函数,且x∈(-∞,0)时,f(x)=-xlg(2-x),求f(x).
∵f(x)为奇函数
∴f(0)=0
当x>0时,-x<0,
f(-x)=xlg(2+x)
即-f(x)=xlg(2+x)
∴f(x)=-xlg(2+x)(x>0)
∴f(x)=-xlg(2-x)(x<0)
-xlg(2+x)(x≥0)
三、周期性
①定义在R上的函数f(x)
Ⅰ若有两条对称轴x=a,x=b,则f(x)是周期函数且2|a-b|是它的一个周期.
Ⅱ若有两个对称中心(a,0)(b,0),则f(x)是周期函数且2|a-b|是它的一个周期
Ⅲ若有一个对称中心(a,0)和一条对称轴x=b,则f(x)是周期函数且4|a-b|是它的一个周期.
②若对于函数f(x)的定义域内任一自变量的值x都有f(x+a)=-f(x)或f(x+a)=1/f(x)或f(x+a)=-1/f(x)(a是常数且a≠0),则f(x)是以2a为一个周期的周期函数.
四、对称性
①函数f(x)满足f(-x)=-f(x),则图像关于原点对称.
②函数f(x)满足f(-x)=f(x),则图像关于y轴对称.
③若函数f(x)满足f(x)=f^(-1)(x),则图像关于直线y=x对称.④若函数f(x)满足f(a+x)=fb-(x),则图像关于x=(a+b)/2对称.
④若函数f(x)满足f(a+x)=-f(b-x),则图形关于点((a+b)/2,0)对称.
五、凸凹性
凸函数:f[(X1+X2)/2]≥[f(X1)+f(X2)]/2
凹函数:f[(X1+X2)/2]≤[f(X1)+f(X2)]/2
拓展形式:jensen不等式
六、图像变换
Ⅰ平移变换:
①y=f(x)的图像向左平移a(a>0)个单位得到函数y=f(x+a)的图像.
②y=f(x-b)(b>0)的图像可由y=f(x)的图像向右平移b个单位得到.
口诀:左加右减、上加下减
(LZ经验:对于y=f(-x)的图像变换恰与上述相反,不论是y=f(x)或y=f(-x)的变换都是对自变量x的变换,一般将x前的系数提出来,若为x+k,则为x向左移k个单位;若为x-k,则为x向右移k个单位)(三角函数)
Ⅱ对称变换
①y=f(-x)与y=f(x)的图像关于y轴对称;
②y=-f(x)与y=f(x)的图像关于x轴对称;
③y=-f(-x)与y=f(x)的图像关于原点对称;
④y=f^(-1)(x)[反函数]与y=f(x)的图像关于直线y=x对称;
⑤y=|f(x)|的图像:可将y=f(x)的图像在x轴下方的部分关于x轴翻转180度,其余部分不变;
⑥y=f(|x|)的图像:可先作出y=f(x)(x≥0)的图像,再利用偶函数的图像关于y轴对称,作出y=f(x)(x≤0)的图像.
Ⅲ伸缩变换
①y=Af(x)(A>0)的图像,可将y=f(x)的图像上所以点的纵坐标变为原来的A倍,横坐标不变而得到;
②y=f(ax)(a>0)的图像,可将y=f(x)的图像上所有点的横坐标变为原来的1/a,纵坐标不变而得到.
-
高中数学函数总结归纳
大成培训(函数总结归纳)一:会求函数的定义域值域。二:知道函数奇偶性的相关性质。三:会求函数的导数和用导数解决相关问题,会解含x3…
-
初中数学函数总结 形如y
初中数学函数总结形如y=kx(k为常数,且k不等于0),y就叫做x的正比例函数。图象做法:1。带定系数2。描点3。连线图象是一条直…
-
初中二次函数总结
二次函数一、函数定义与表达式1.一般式:y?ax2?bx?c(a,b,c为常数,a?0);2.顶点式:y?a(x?h)2?k(a,…
-
一元二次函数总结
一、二次函数的定义一般地,如果y=ax2+bx+c(a、b、c是常数,a≠0),那么y叫做x二次函数。注:二次函数y=ax2+bx…
-
数据库函数总结
1、将字段的值转换为汉字的函数:F_get_value(‘字段’,’’)Decode(‘’,’’,’’,’’,…)eg:f_get…
-
函数图像总结
高一数学函数图像知识点总结一、函数图像知识点汇总1.函数图象的变换1平移变换①水平平移:y=fxaa>0的图象,可由y=fx的图象…
-
高一必修四函数及其函数图像总结
诱导公式:奇变偶不变,符号看象限。①看是π/2的几倍,奇数倍变名,偶数倍不变。②符号看变之前的。③x永远当锐角。一.正弦函数:形如…