数值分析考试复习总结
第一章
1 误差
相对误差和绝对误差得概念
例题:当用数值计算方法求解一个实际的物理运动过程时, 一般要经历哪几个阶段? 在哪些阶段将有哪些误差产生?
答: 实际问题-数学模型-数值方法-计算结果
在这个过程中存在一下几种误差:
建立数学模型过程中产生:模型误差 参数误差
选用数值方法产生:截断误差
计算过程产生:舍入误差 传播误差
6.设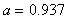 关于精确数
关于精确数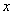 有3位有效数字,估计
有3位有效数字,估计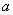 的相对误差. 对于
的相对误差. 对于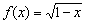 ,估计
,估计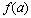 对于
对于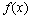 的误差和相对误差.
的误差和相对误差.
解 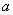 的相对误差:由于
的相对误差:由于
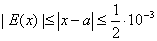 .
. 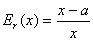 ,
,
 . (
. (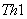 )
)
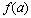 对于
对于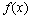 的误差和相对误差.
的误差和相对误差. 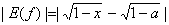 =
=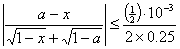 =
=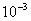
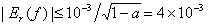 .
.
2有效数字 基本原则:1 两个很接近的数字不做减法: 2: 不用很小得数做分母(不用很大的数做分子)
例题:
4.改变下列表达式使计算结果比较精确:
(1) 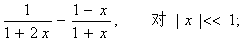
(2) 
(3) 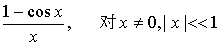 .
.
解 (1) 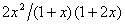 . (2)
. (2) 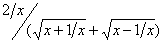 .
.
(3) 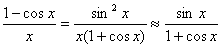 . □
. □
第二章
拉格朗日插值公式(即公式(1)) 
插值基函数(因子)可简洁表示为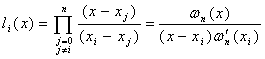
其中: 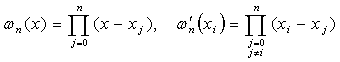 .
.
例1 n=1时,线性插值公式  ,
,
例2 n=2时,抛物插值公式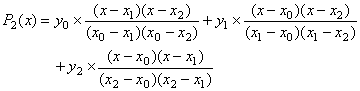
牛顿(Newton)插值公式;由差商的引入,知
(1) 过点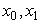 的一次插值多项式为
的一次插值多项式为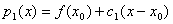
其中
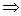
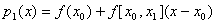
(2) 过点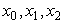 的二次插值多项式为
的二次插值多项式为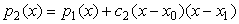
其中 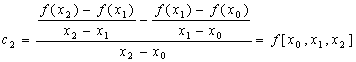
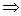

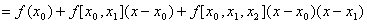
重点是分段插值:
例题:1. 利用Lagrange插值公式求下列各离散函数的插值多项式(结果要简化):


解(2): 方法一. 由 Lagrange 插值公式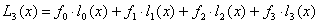
可得: 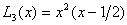
方法二. 令 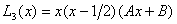
由 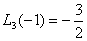 ,
, 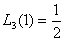 , 定A,B (称之为待定系数法)
, 定A,B (称之为待定系数法)
15.设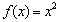 ,求
,求 在区间
在区间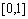 上的分段线性插值函数
上的分段线性插值函数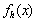 ,并估计误差,取等距节点,且
,并估计误差,取等距节点,且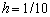 .
.
解 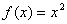 ,
, 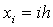 ,
,  ,
, 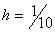
设 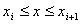 ,则:
,则: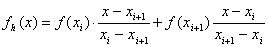


误差估计: 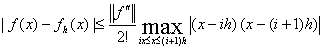 . □
. □
第四章
1 为什么要进行数值积分?常用哪些公式,方法?
答: 梯形复化求积公式和simpson复化求积公式.
2: 方法好坏的判断: 代数精度
l 误差分析
1.代数精度的概念
定义:若求积公式 (*)对所有次数
(*)对所有次数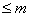 的多项式是精确的,但对
的多项式是精确的,但对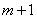 次多项式不精确,则称(*)具有
次多项式不精确,则称(*)具有 次代数精度。
次代数精度。
等价定义:若求积公式(*)对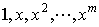 是精确的,但对
是精确的,但对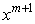 不精确,则(*)具有
不精确,则(*)具有 次代数精度。
次代数精度。
3: 误差
1 等距剖分下的数值求积公式:
公式特点:节点预先给定,均匀分布,系数 待定
待定
利用插值多项式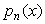 近似代替
近似代替 ,即得插值型求积公式Newton-Cotes公式
,即得插值型求积公式Newton-Cotes公式
2 给定节点数下的具有最佳逼近性质(具有最高次代数精度)的数值求积公式:Gauss求积公式 公式特点:系数 和节点
和节点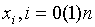 均待定
均待定
3 分段插值多项式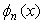 近似代替
近似代替 (分段求积)复化求积公式
(分段求积)复化求积公式
复化求积公式
通过高次求积公式提高精度的途径不行,类似函数插值
分而治之: 分段+低次求积公式---------- 称为复化求积法
两类低次(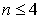 )求积公式:
)求积公式:
1. Newton-Cotes型:矩形、梯形、Simpson、Cotes公式分别称为复化矩形、梯形、辛甫生、柯特斯公式
2. Gauss型: 一点、两点、三点Gauss求积公式称为复化一点、两点、三点Gauss公式
复化梯形公式(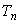 )
)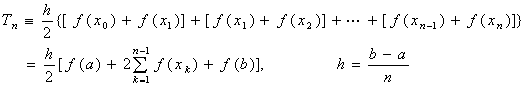
复化辛甫生公式: (每个 上用辛甫生公式求积)
上用辛甫生公式求积)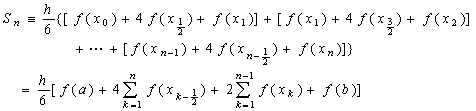
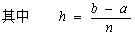 ,
,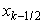 为
为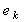 的中点
的中点
复化辛甫生公式是最常用的数值求积方法。常采用其等价形式:
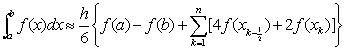
复化柯特斯公式

其中,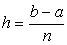 ,
,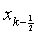 为
为 的中点,
的中点,
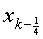 ,
,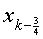 为
为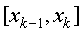 的四等分的分点
的四等分的分点
l 自适应复化求积法
计算时,要预先给定 或步长
或步长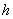 ,在实际中难以把握
,在实际中难以把握
因为,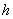 取得太大则精度难以保证,
取得太大则精度难以保证,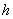 太小则增加计算工作量.
太小则增加计算工作量.
自适应复化梯形法的具有计算过程如下:
步1 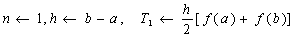
步2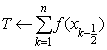
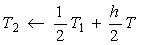
步3 判断 ?若是,则转步5;
?若是,则转步5;
步4 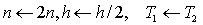 ,转步2;
,转步2;
步5 输出 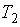 .
.
第五章
1: 常用方法:
(1).直接解法: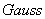 逐步(顺序)消去法、
逐步(顺序)消去法、
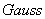 主元素法、矩阵分解法等;
主元素法、矩阵分解法等;
(2).迭代解法:构造某种极限过程去逐步逼近方程组的解
①.经典迭代法
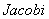 迭代法、
迭代法、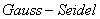 迭代法、
迭代法、
逐次超松弛(SOR)迭代法等;
②. Krolov子空间的迭代法
根据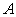 的对称性,又分为:
的对称性,又分为:
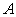 对称正定------- 共轭梯度法
对称正定------- 共轭梯度法
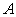 非对称--------- BICG 、 GMRes(最小残量法)
非对称--------- BICG 、 GMRes(最小残量法)
③.解一类特定背景问题的迭代法
多重网格法
2: 几类迭代法优缺点比较:
3: 迭代方法
目标: 求解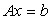 其中,
其中,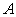 非奇异。
非奇异。
基本思想:把线性方程组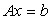 的解
的解 ,化为一个迭代序列极限解
,化为一个迭代序列极限解
关键:构造迭代序列所满足的公式:迭代格式。
构造迭代格式基本步骤:
1. 将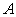 分裂:
分裂: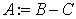 , 其中,
, 其中, 非奇异
非奇异
2. 构造迭代格式
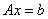
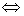
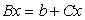
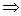
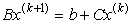
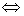
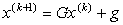
其中 ,称之为迭代矩阵 ,
,称之为迭代矩阵 , 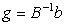
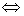
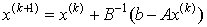
其中, 为
为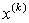 的残余向量
的残余向量
此时,
常用的迭代方法
将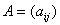 分裂为
分裂为
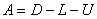 其中
其中
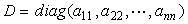
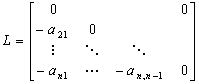 ,
, ,
,
l Jacobi迭代方法

若 ,迭代格式
,迭代格式
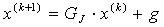 ①
①
其中 Jacobi迭代矩阵: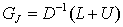
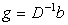
①式可写为分量形式
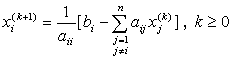 . (*1)
. (*1)
方法(*1)或①称为Jacobi迭代方法.
Gauss—Seidle迭代方法
若 ,迭代格式
,迭代格式
 ②
②
其中,
Gauss-Seidel迭代矩阵: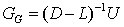

其分量形式
 ,
,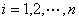 . (*2)
. (*2)
即,
在计算新分量 时,利用新值
时,利用新值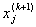 ,
,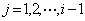 。
。
迭代法(*2)或②称为Gauss—Seidel迭代方法 。
l 超松弛方法(SOR)方法
定义SOR方法的迭代格式如下:
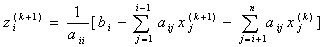 ,
,
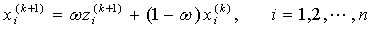 (*3)
(*3)
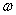 称为松弛因子,
称为松弛因子, 即为
即为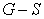 方法.
方法.
其矩阵形式

其中,
SOR法的迭代矩阵: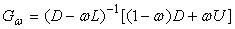

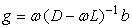 .
.
第七章
1: 解非线性方程与方程组的方法:
1. 准确方法
如:用求根公式对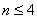 次的代数多项式求根。
次的代数多项式求根。
但: 绝大多数的方程并无准确方法可用。如: 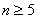 次的代数多项式并无求根公式。
次的代数多项式并无求根公式。
2. 数值方法(实际中大多采用)
基本思想: 设法找到一个能收敛到方程的解的序列。
(1).区间套法—— 二分法。
(2).迭代法:
①.简单迭代法; ②. Newton迭代法;
3. 割线法; 4.加速算法。
2: 收敛条件:
二分法无条件
简单迭代法条件:
定理1 如果  满足以下条件:
满足以下条件:
1) 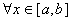 ,
,  ;
;
2) 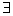 常数
常数 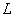 :
:  , 使得对任意两点
, 使得对任意两点 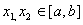 ,都有
,都有
 ,
,
则: 方程(*)在 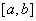 上的解
上的解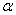 存在唯一,且对任给的初值
存在唯一,且对任给的初值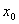 ,由迭代过程(* *) 所产生的序列
,由迭代过程(* *) 所产生的序列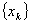 收敛到
收敛到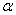 .
.
例题:
2. 为求方程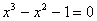 在
在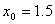 附近的一个根,设将方程改写为下列等价形式,并建立相应的迭代公式:
附近的一个根,设将方程改写为下列等价形式,并建立相应的迭代公式:
(1)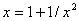 ,迭代公式
,迭代公式 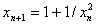
(2) ,迭代公式
,迭代公式 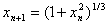 ,
,
(3) ,迭代公式
,迭代公式 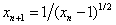 ,
,
试分析每一种迭代公式的收敛性,并问哪一种迭代收敛得快?
解:取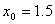 的邻域
的邻域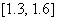 来考察
来考察
(1)  ,
,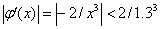
 ,故迭代公式(1)收敛.
,故迭代公式(1)收敛.
(2) 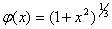 ,
,
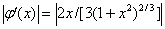
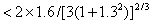
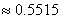 ,
,
故迭代公式(2)也收敛。
(3) 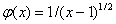 ,
,


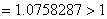
故迭代公式(3)发散.
由于 越小,越快地收敛于根
越小,越快地收敛于根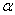 ,故(2)式收敛最快。□
,故(2)式收敛最快。□
第八章
解一阶常微分方程的常用方法: Euler 方法 Runge-Kutta 方法
2阶常微分方程边值问题的差分方法
1. 三类边值问题
1)第一类边值问题:
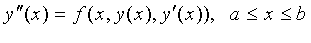 , (3.1)
, (3.1)
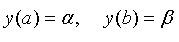 。 (3.2)
。 (3.2)
2)第二类边值问题:
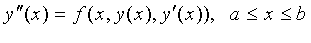 , (3.3)
, (3.3)
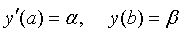 。 (3.4)
。 (3.4)
3)第三类边值问题:
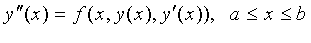 , (3.5)
, (3.5)
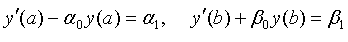 , (3.6)
, (3.6)
其中,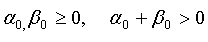 。
。
2. 差分格式的建立
针对方程(3.1)而言.
Step 1 取 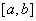 的离散节点:
的离散节点:
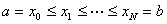 , 第
, 第  步步长
步步长  , 一般可取等
, 一般可取等
步长:  ,
, 
Step 2 将  用二阶差商、
用二阶差商、 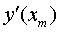 用一阶差商近似:
用一阶差商近似:
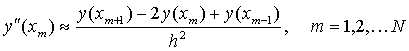 ,
,
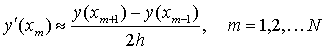 .
.
理由:由Taylor展开,有
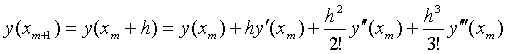

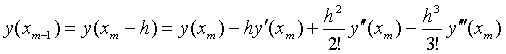
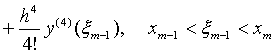
两式相加得
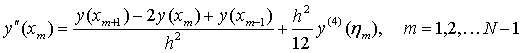
其中,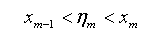 .
.
两式相减得
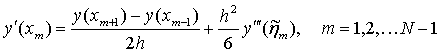 ,
,
其中, .
.
Step 3 略去 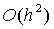 项 , 并记
项 , 并记 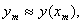 则由方程(3.1)有:
则由方程(3.1)有:
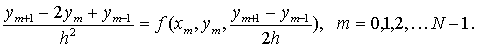 (3.7)
(3.7)
所以得到第一边值问题(3.1)-(3.2)的差分格式:
 …(3.8)
…(3.8)
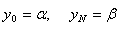 . …………………………(3.9)
. …………………………(3.9)
对第二边值条件(3.3),由于
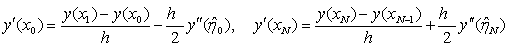
其中,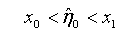 ,
,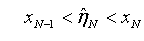 ,
,
已及 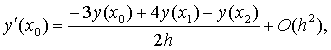

所以可得到第二类边值问题(3.3)-(3.4)的差分格式:
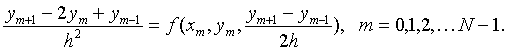 (3.10)
(3.10)
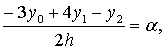
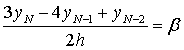 . ……(3.11)
. ……(3.11)
类似可得第三类边值问题(3.5)-(3.6)的差分格式(略).
-
高三物理12月考试分析总结报告
茂名市第五中学高三物理12月月考分析总结一、上课备考情况目前已经复习到第五章机械能的内容,自期中考试以来,主要就选择题进行专项的测…
-
高中语文教师高三考试分析总结
博观约取厚积薄发荆州是第一次调考的硝烟已经散去,可一调留给我们的思考却不会因为时间而淡忘,牛顿面对自己的成功,曾说“我是站在巨人的…
-
20xx年物理一模考试分析总结[1]
20xx年物理一模考试分析总结那勤中学陈业权20xx年防城港市一模调研考试中,从试卷总体难易程度看:有12分是较难题,其余都是中档…
-
高一语文期中考试分析总结
李明波按照学校的安排,为了总结经验吸取教训,更好地完成高一下学期的教学任务,我对这次期中考试的成绩进行分析,找出考试中反映出来的问…
-
九年级半期考试分析总结
本次数学考试总分150分,其中及格的人数为,优生人数为10人,差生人数为。比起第一次月考,总的成绩当然好得多。但是,这成绩其实一样…
-
数值分析课程总结
课程内容1误差了解误差的来源与分类及误差的基本概念与性质;熟悉绝对误差及绝对误差限、相对误差及相对误差限和有效数字之间的关系;掌握…
-
数值分析学习总结感想
数值分析学习感想摘要数值分析主要介绍现代科学计算中常用的数值计算方法及其基本原理研究并解决数值问题的近似解是数学理论与计算机和实际…
-
数值分析学习报告
数值分析学习心得报告班级姓名学号学习数值分析的心得体会数值分析是一门利用计算机求解数学问题数值解的课程有很强的理论性和实践性无意中…
-
数值分析期末总结论文,程序界面
数值计算方法论文论文名称数值计算方法期末总结学号姓名完成时间摘要数值计算方法是数学的一个重要分支以用计算机求解数学问题的理论和方法…
-
数值分析编程总结
1.LU分解:[LU]=lu(A);2.追赶法functionx=zhuiganfa(A,b)[n,n]=size(A);fori…