数值分析(颜庆津)第三章 学习小结
第三章矩阵特征值与特征向量的计算
--------学习小结
一、 本章学习体会
通过本章的学习,我们学到了四种矩阵特征值和特征向量的计算方法,分别是幂法、反幂法、Jacobi方法和QR方法。
四种方法各有其特点和适用范围。幂法主要用于计算矩阵按模最大的特征值及其相应的特征向量;反幂法主要用于计算矩阵按模最小的特征值及其相应的特征向量;Jacobi方法用于求实对称矩阵的全部特征值和特征向量的方法;QR方法则适用于计算一般实矩阵的全部特征值,尤其适用于计算中小型实矩阵的全部特征值。归结起来,这四种方法亦有其共同点,那就是都是用了迭代的方法来求矩阵的特征值和特征向量。
此外,用MATLAB自带的解法求解特征值和特征向量也非常快速,而且不用编辑函数建立m文件。其自带函数Eig功能强大,即便得到结果是虚数也可以算出,并且结果自动正交化。
二、 本章知识梳理
本章对于矩阵的特征值和特征向量的算法提出了新的思路,如幂法和反幂法、Jacobi、QR方法等。本章的小结主要从方法的思想,以及一些定理展开。
2.1各种方法的运用范围
1、幂法:主要用于计算矩阵按模最大的特征值和其相应的特征向量;
2、反幂法:主要计算矩阵按模最小的特征值以及其相应的特征向量;
3、Jacobi方法:用于求实对称矩阵的全部特征值和特征向量的方法;
4、QR方法:适用于计算一般实矩阵的全部特征值,尤其适用于计算中小型实矩阵的全部特征值。
2.2各种方法的基本思想以及迭代公式
1.幂法
幂法的基本思想:
设n×n实矩阵A具有n个线性无关的特征向量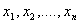 ,其相应的特征值
,其相应的特征值 满足不等式
满足不等式
 ,其中
,其中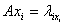
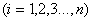 。
。
任取一n维非零向量u0,从u0出发,按照如下的递推公式
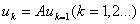
因n维向量组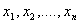 线性无关,故对向量u0必存在唯一的不全为0的数组a1,a2,…,an,使得
线性无关,故对向量u0必存在唯一的不全为0的数组a1,a2,…,an,使得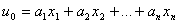
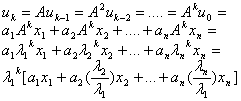
设a1≠0,由上式可以看出,当k充分大时有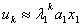
得迭代公式: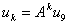 (1)
(1)
从实际中来看,为了避免迭代向量uk的模过大,(当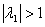 )或过小(当
)或过小(当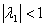 ),通常对ukj进行归一化,使其范数等于1。
),通常对ukj进行归一化,使其范数等于1。
幂法的迭代公式:
(1)用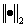 范数来归一,并且令
范数来归一,并且令
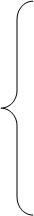 任取非零向量
任取非零向量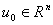

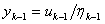
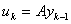

(k=1,2,..)
(2) 用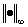 范数来归一,并且令:
范数来归一,并且令: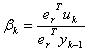
 任取非零向量
任取非零向量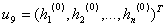
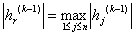
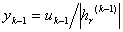


(k=1,2,…)
上述两种迭代终止控制用 ,以当前的
,以当前的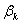 和
和 分别作为
分别作为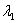 和相应的特征向量。
和相应的特征向量。
两种方法的比较:
(1)迭代格式编制程序容易,但迭代一次时间较长,(2)迭代格式每迭代一次都要判断上一个哪一个分量的模最大,因而时间长,但在运算的摄入误差中影响比(1)迭代格式影响小。
2.反幂法
反幂法的基本思想:
反幂法的基本思想与幂法基本相同,一个是利用模最大的特征值,一个是利用模最小的特征值。
设n×n实矩阵A具有n个线性无关的特征向量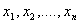 ,其相应的特征值
,其相应的特征值 满足不等式
满足不等式
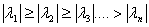 ,其中
,其中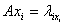
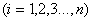 。
。
得: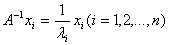
此时, 是矩阵
是矩阵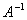 的按模最大的特征值,我们就将问题转化为了幂法的思想。
的按模最大的特征值,我们就将问题转化为了幂法的思想。
反幂法的迭代公式
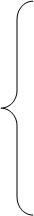 任取非零向量
任取非零向量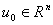

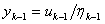
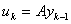

(k=1,2,..)
2.3Jacobi方法
1.Jacobi方法的基本思想:
任一实对称矩阵正交相似于对角阵。Jacobi用适当选取的平面旋转变换将给定的实对称矩阵逐步化为对角阵。
2.求实对称矩阵A的特征值与相应的特征向量是一个迭代过程,其迭代步骤为:
(1) 在A的非对角线元素中,找出按模最大的元素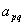 ;
;
(2)由 计算
计算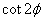 ,比由此计算出
,比由此计算出 以及相应的平面旋转矩阵;
以及相应的平面旋转矩阵;
(3)计算出矩阵A1的元素 ;
;
(4)若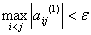 ,则停止运算,所求特征值为
,则停止运算,所求特征值为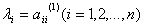 ,则令A=A1,重复执行上述过程。
,则令A=A1,重复执行上述过程。
3.Jacobi方法的一些说明
设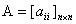 是实对称矩阵,由Jacobi方法的第k次迭代得到的矩阵记为
是实对称矩阵,由Jacobi方法的第k次迭代得到的矩阵记为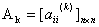 ,又记为
,又记为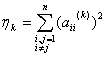 则有
则有 成立。
成立。
优点:
前面论述的Jacobi方法,每次迭代都是按模最大的对角线元素作为消元对象,不论实对称矩阵A的特征值如何分布,这种方法总是收敛的,当A得阶数不是很高时。收敛速度还比较快,而且这种方法有数值稳定性,计算精度一般比较高,特别是求的的特征向量正交性比较好。
缺点:
不能有效的利用矩阵的各种特殊形状,浪费时间。
2.4QR方法:
1.QR 方法的基本思想:
任何n×n的实矩阵总可以分解成一个正交矩阵Q和一个上三角矩阵R的乘积。QR方法最重要的一步是对A进行正交分解使得A=QR,其中Q为一特殊正交矩阵。理论上,QR方法可以应用于任何矩阵,但对以下几类矩阵效率很高:1)对称三对角矩阵;2)Hessenberg矩阵;3)对称带状矩阵。
(实Schur分解定理):
设A是一个n阶实方阵,那么存在一个正交矩阵Q使得A相似于

其中对角块为一阶或二阶方阵,每一个一阶对角块对应于A的一个实特征值,每一个二阶对角块的两个特征值是A的一对共轭复特征值。
2.QR方法的一般形式:
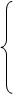
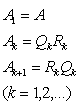
对任意实方阵A,由QR方法产生的矩阵序列{Ak}本质上收敛于分块上三角矩阵(对角块以上的元素可能不收敛),其中对角块为一阶或二阶方阵,每一个一阶对角块对应于A的一个实特征值,每一个二阶对角块的两个特征值是A的一对共轭复特征值。
3.Householder变换(矩阵)
设υ为n维单位向量,即υT υ=1 ; H=1-2υυT
(1) Householder矩阵是正交矩阵;
(2) 对任意的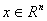 ,记
,记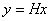 ,有
,有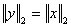 ;
;
(3) 记S为与w垂直的平面,则几何上x与y=Hx关于平面S对称。事实上,由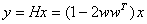 得知:
得知:
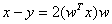
设有非零向量s和单位向量e,则必存在Householder矩阵H使得Hs=±αe,其中α是实数且 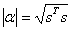
设A是一个n阶实方阵,那么A可分解为一个正交矩阵Q和一个上三角矩阵R的乘积,A=QR。
三、 本章思考题
幂法计算矩阵特征值和特征向量的基本思想是设n×n实矩阵A具有n个线性无关的特征向量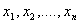 ,其相应的特征值为
,其相应的特征值为 ,任取一n维非零向量u0,从u0出发,按照递推公式
,任取一n维非零向量u0,从u0出发,按照递推公式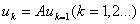 。因n维向量组
。因n维向量组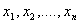 线性无关,故对向量u0必存在唯一的不全为0的数组a1,a2,…,an,使得
线性无关,故对向量u0必存在唯一的不全为0的数组a1,a2,…,an,使得 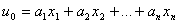
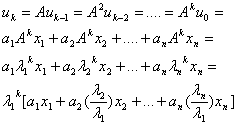
设a1≠0,由上式可以看出,当k充分大时有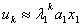 ,得迭代公式:
,得迭代公式: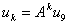 。 从实际中来看,为了避免迭代向量uk的模过大,(当
。 从实际中来看,为了避免迭代向量uk的模过大,(当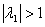 )或过小(当
)或过小(当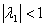 ),通常对ukj进行归一化,使其范数等于1。
),通常对ukj进行归一化,使其范数等于1。
一般来说,我们都使用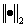 或者
或者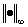 范数来归一,如果我们用
范数来归一,如果我们用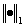 范数来归一会出现什么效果呢?
范数来归一会出现什么效果呢?
思路:
以一定的方式,构造一个初值和一个迭代公式,将初值带入迭代公式,持续一定次数后,两次迭代的结果的误差达到一定值时,迭代终止。得出相应的特征值和特征向量。
四、 本章测验题
Jacobi方法是用于求()的全部特征值和特征向量的一种方法。
A.正交矩阵 B.实对称矩阵
C.上三角矩阵 D.下三角矩阵
答案:B.实对称矩阵
第二篇:数值分析的一个小结
InterpolationandPolynomialApproximation
XueJingnan(200805090173)
April1,2011
Abstract
Inthisreport,wereviewedthreedi?erentinterpolationsandpolynomialap-proximations[1]respectively,say,LagrangePolynomial,HermiteInterpolationandCubicSplineInterpolation.Weintroducedtheiralgorithmdescriptions,relatedmathematicaldeductionsandapplicationstopracticalproblemsrespec-tively.Moreover,abriefdiscussionoftheiradvantagesandlimitsarepresentedatlast.
Contents
1Introduction
2InterpolationandtheLagrangePolynomial
2.1Mathematicaldeduction.......................
2.2Numericalexperiments........................
2.2.1Example1...........................
2.2.2Example2...........................3HermiteInterpolation
3.1Mathematicaldeduction.......................
3.2Algorithmdescription........................
3.2.1pseudocode..........................
3.2.2code..............................
3.3Numericalexperiments........................
3.3.1Example1...........................
3.3.2Example2...........................4CubicSplineInterpolation
4.1Mathematicaldeduction.......................
4.2Algorithmdescription........................
4.2.1pseudocode..........................
4.2.2code..............................
4.3Numericalexperiments........................
4.3.1Example1...........................
4.3.2Example2...........................5DiscussionandConclusion
5.1InterpolationandtheLagrangePolynomial............
5.2HermiteInterpolation........................
5.3CubicSplineInterpolation......................
124xxxxxxxxxxxx21213161xxxxxxxxxxxx23232323
Chapter1
Introduction
Oneofthemostusefulandwell-knownclassesoffunctionsmappingthesetofrealnumbersintoitselfistheclassofalgebraicpolynomials,thesetoffunctionsoftheform
Pn(x)=anxn+an?1xn?1+···+a1x+a0
wherenisanonnegativeintegeranda0,...,anarerealconstants.Onereasonfortheirimportanceisthattheyuniformlyapproximatecontinuousfunctions.Givenanyfunction,de?nedandcontinuousonaclosedandboundedinter-val,thereexistsapolynomialthatisas”close”tothegivenfunctionasdesired.Anotherimportantreasonforconsideringtheclassofpolynomialsintheapprox-imationoffunctionsisthatthederivativeandinde?niteintegralofapolynomialareeasytodetermineandarealsopolynomials.Forthesereasons,polynomialsareoftenusedforapproximatingcontinuousfunctions.
Inthisreport,wediscussedapproximatingafunctionusingpolynomialsandpiecewisepolynomials.Thefunctioncanbespeci?edbyagivende?ningequationorbyprovidingpointsintheplanethroughwhichthegraphofthefunctionpasses.Asetofnodesx0,x1,···,xnisgivenineachcase,andmoreinformation,suchasthevalueofvariousderivatives,mayalsoberequired.Weneedto?ndanapproximatingfunctionthatsatis?estheconditionsspeci?edbythesedata
TheinterpolatingpolynomialP(x)isthepolynomialofleastdegreethatsatis?es,forafunctionf,
P(xi)=f(xi),foreachi=0,1,...,n.
Althoughthisinterpolatingpolynomialisunique,itcantakemanydi?erentforms.TheLagrangeformismostoftenusedforinterpolatingtableswhennissmallandforderivingformulasforapproximatingderivativesandintegrals.Neville’smethodisusedforevaluatingseveralinterpolatingpolynomialsforcomputationandarealsousedextensivelyforderivingformulasforsolvingdi?erentialequations.TheHermitepolynomialsinterpolateafunctionandits
2
CHAPTER1.INTRODUCTION3derivativeatthenodes.Theycanbeveryaccuratebutrequiremoreinformationaboutthefunctionbeingapproximated.Whentherearealargenumberofnodes,theHermitepolynomialsalsoexhibitoscillationweaknesses.
However,polynomialinterpolationhastheinherentweaknessesofoscillation,particularlyifthenumberofnodesislarge.Inthiscase,thereareothermethodsthatcanbebetterapplied,themostcommonlyusedoneofwhichispiecewise-polynomialinterpolation.Iffunctionandderivativevaluesareavailable,piece-wisecubicHermiteinterpolationisrecommended.Thisisthepreferredmethodforinterpolatingvaluesoffunctionthatisthesolutiontoadi?erentequation.Whenonlythefunctionvaluesareavailable,freecubicsplineinterpolationcanbeused.Thissplineforcesthesecondderivativeofthesplinetobezeroattheendpoints.Othercubicsplinesrequireadditionaldata.Forexample,theclampedcubicsplineneedsvaluesofthederivativeofthefunctionattheend-pointsoftheinterval.
Chapter2
InterpolationandtheLagrangePolynomial
2.1Mathematicaldeduction
Theproblemofdeterminingapolynomialofdegreeonethatpassesthroughthedistinctpoints(x0,y0)and(x1,y1)isthesameasapproximatingafunctionfforwhichf(x0)=y0andy(x1)=y1bymeansofa?rst-degreepolynomialinterpolating,oragreeingwith,oragreeingwith,thevaluesoffatthegivenpoints.We?rstde?nethefunctions
L0(x)=
andthende?ne
P(x)=L0(x)f(x0)+L1(x)f(x1).
Since
L0(x0)=1,L0(x1)=0,L1(x0)=0,
wehave
P(x0)=1·f(x0)+0·f(x1)=f(x0)=y0
and
P(x1)=0·f(x0)+1·f(x1)=f(x1)=y1
SoPistheuniquelinearfunctionpassingthrough(x0,y0)and(x1,y1).Togeneralizetheconceptoflinearinterpolation,considertheconstructionofapolynomialofdegreeatmostnthatpassesthroughthen+1points
(x0,f(x0),(x1,f(x1),...(xn,f(xn).
Inthiscaseweneedtoconstruct,foreachk=0,1,...,n,afunctionLn,k(x)withthepropertythatLn,k(xi)=0wheni=kandLn,k(xk)=1.Tosatisfy
4andL1(x1)=1,x?x1x0?x1andL1(x)=x?x0x1?x0
CHAPTER2.INTERPOLATIONANDTHELAGRANGEPOLYNOMIAL5Ln,k(xi)=0foreachi=krequiresthatthenumeratorofLn,k(x)containstheterm
(x?x0)(x?x1)(x?x2)···(x?xk?1)(x?xk+1)···(x?xn).
TosatisfyLn,k(x)=1,thedenominatorofLn,k(x)mustbeequaltothistermevaluatedatx=xk.Thus,
Ln,k(x)=(x?x0)(x?x1)(x?x2)···(x?xk?1)(x?xk+1)···(x?xn).(xk?x0)(xk?x1)(xk?x2)···(xk?xk?1)(xk?xk+1)···(xk?xn)
TheinterpolatingpolynomialiseasilydescribedoncetheformofLn,kisknown.Thispolynomial,calledthenthLagrangeinterpolatingpolyno-mial,isde?nedinthefollowingtheorem.
Theorem2.1Ifx0,x1,···,xnaren+1distinctnumbersandfisafunctionwhosevaluesaregivenatthesenumbers,thenauniquepolynomialP(x)ofdegreeatmostnexistswith
f(xk)=P(xk),
Thispolynomialisgivenby
P(x)=f(x0)Ln,0(x)+···+f(xn)Ln,n(x)=
where,foreachk=0,1,···,n,
Ln,k(x)=(x?x0)(x?x1)(x?x2)···(x?xk?1)(x?xk+1)···(x?xn)
(xk?x0)(xk?x1)(xk?x2)···(xk?xk?1)(xk?xk+1)···(xk?xn)n?x?xi.=x?xkii=0i=kn?k=0foreachk=0,1,...,n.f(xk)Ln,k(x),(2.1)
(2.2)
WewillwriteLn,k(x)simplyasLk(x)whenthereisnoconfusionastoitsdegree
2.2
2.2.1NumericalexperimentsExample1
Usingthenumbers(ornodes)x0=2,x1=2.5,andx2=4to?ndthesecondin-terpolatingpolynomialforf(x)=1/xrequiresthatwedeterminethecoe?cientpolynomialsL0(x),L1(x),andL2(x).Innestedformtheyare
(x?2.5)(x?4)=(x?6.5)x+10,(2?2.5)(2?4)
(?4x+24)x?32(x?2)(x?4)L1(x)==,(2.5?2)(2.5?4)3L0(x)=
CHAPTER2.INTERPOLATIONANDTHELAGRANGEPOLYNOMIAL6and
L2(x)=(x?2)(x?2.5)(x?4.5)x+5=(4?2)(4?2.5)3
Sincef(x0)=f(2)=0.5,f(x1)=f(2.5)=0.4,andf(x2)=f(4)=0.25,wehave
P(x)=2?
k=0f(xk)Lk(x)
(x?4.5)x+5(?4x+24)x?32)+0.2533=0.5((x?6.5)x+10)+0.4(
=(0.05x?0.425)x+1.15.
Anapproximationtof(3)=1/3is
f(3)≈P(3)=0.325
2.2.2Example2
Forthegivenfunctionsf(x),letx0=0,x1=0.6,andx2=0.9.Constructinterpolationpolynomialsofdegreeatmosttwotoapproximatef(0.45),and?ndtheactualerror.
(1)
(2)
(3)
(4)f(x)=cosx√f(x)=f(x)=ln(x+1)f(x)=tanx
Atthebeginning,wedeterminedthecoe?cientpolynomialsL0(x),L1(x),andL2(x).Innestedformtheyare
50(x?0.6)(x?0.9)=[(x?1.5)x+0.54]+10,(0?0.6)(0?0.9)27
(x?0)(x?0.9)50L1(x)==?(x?0.9)x)(0.6?0)(0.6?0.9)9
(x?0)(x?0.6)100L2(x)==(x?0.6)x(0.9?0)(0.9?0.6)27L0(x)=
(1)f(x)=cosx
Sincef(x0)=f(0)=1,f(x1)=f(0.6)=cos(0.6)≈0.8253,
andf(x2)=f(0.9)≈0.6216,wehave
P(x)=2?
k=0f(xk)Lk(x)
≈(5010050[(x?1.5)x+0.54]+0.8253[?(x?0.9)x)]+0.6216[(x?0.6)x]27927
≈(?0.4309x?0.0326)x+1
CHAPTER2.INTERPOLATIONANDTHELAGRANGEPOLYNOMIAL7
Anapproximationtof(0.45)=cos(0.45)=0.9004is
f(0.45)≈P(0.45)=0.8980
Andtheactualerrorisf(0.45)?P(0.45)=2.4×10?3
√(2)f(x)=Sincef(x0)=f(0)=1,f(x1)=f(0.6)≈1.2649,
andf(x2)=f(0.9)≈1.3784,wehave
P(x)=2?
k=0f(xk)Lk(x)
≈(5010050[(x?1.5)x+0.54]+1.2649[?(x?0.9)x)]+1.3784[(x?0.6)x]≈(?0.0702x+0.4836)x+1
Anapproximationtof(0.45)=1.2042is
f(0.45)≈P(0.45)=1.2034
Andtheactualerrorisf(0.45)?P(0.45)=7.955×10?4
(3)f(x)=ln(1+x)
Sincef(x0)=f(0)=0,f(x1)=f(0.6)≈0.4700,
andf(x2)=f(0.9)≈0.6419,wehave
P(x)=2?
k=0f(xk)Lk(x)
≈0.4700[?10050(x?0.9)x)]+0.6419[(x?0.6)x]927
≈(?0.2337x+0.9236)x
Anapproximationtof(0.45)=0.3716is
f(0.45)≈P(0.45)=0.3683
Andtheactualerrorisf(0.45)?P(0.45)=3.3×10?3
(4)f(x)=tanx
Sincef(x0)=f(0)=0,f(x1)=f(0.6)≈0.6841,
andf(x2)=f(0.9)≈1.2602,wehave
P(x)=2?
k=0f(xk)Lk(x)
≈0.6841[?10050(x?0.9)x)]+1.2602[(x?0.6)x]927
≈(0.8669x+0.6200)x
CHAPTER2.INTERPOLATIONANDTHELAGRANGEPOLYNOMIAL8
Anapproximationtof(0.45)=0.4830is
f(0.45)≈P(0.45)=0.4545
Andtheactualerrorisf(0.45)?P(0.45)=0.0285
Chapter3
HermiteInterpolationLetx0,x1,...,xnben+1distinctnumbersin[a,b]andmibeanonnegativeintegerassociatedwithxi,fori=0,1,...,n.Supposethatf∈Cm[a,b],wherem=max0≤i≤nmi.TheosculatingpolynomialapproximatingfisthepolynomialP(x)ofleastdegreesuchthat
dkP(xi)dkf(xi)=,dxkdxkforeachi=0,1,...,nandk=0,1,...,nNotethatwhenn=0,theosculatingpolynomialapproximatingfisthem0thTaylorpolynomialforfatx0.Whenmi=0foreachi,theosculatingpolynomialisthenthLagrangepolynomialinterpolatingfonx0,x1,...,xnThecasewhenmi=1,foreachi,givestheHermitepolynomials.Foragivenfunctionf,thesepolynomialsagreewiththoseoff,theyhavethesame”shape”asthefunctionat(xi,f(xi))inthesensethatthetangentlinestothepolynomialandtothefunctionagree.Wewillrestrictourstudyofosculatingpolynomialstothissituation.
3.1Mathematicaldeduction
Firstly,consideratheoremthatdescribespreciselytheformoftheHermitepolynomials.
Theorem3.1Iff∈C1[a,b]andx0,...,xn∈[a,b]aredistinct,theuniquepolynomialofleastdegreeagreeingwithfandf?atx0,...,xnistheHermitepolynomialofdegreeatmost2n+1givenby
H2n+1(x)=
wheren?j=0f(xj)Hn,j(x)+n?j=0?n,j(x)f?(xj)H2Hn,j(x)=[1?2(x?xj)L?n,j(xj)]Ln,j(x)
9
CHAPTER3.HERMITEINTERPOLATION
and10?n,j(x)=(x?xj)L2Hn,j(x)
Inthiscontext,Ln,j(x)denotesthejthLagrangecoe?cientpolynomialofdegreende?nedinChapter2.
Moreover,iff∈C2n+2[a,b],then
(x?x0)2...(x?xn)22n+2f(ξ)f(x)=H2n+1(x)+(2n+2)!
forsomeξwitha<ξ<b
AlthoughTheorem3.1providesacompletedescriptionoftheHermitepoly-nomials,itisclearthattheneedtodetermineandevaluatetheLagrangepoly-nomialsandtheirderivativesmakestheproceduretediousevenforsmallvaluesofn.AnalternativemethodforgeneratingHermiteapproximationshasasitsbasistheNewtoninterpolatorydivided-di?erenceformulafortheLagrangepolynomialatx0,x1,...,xn,
Pn(x)=f[x0]+n?
k=1f[x0,x1,...,xk](x?x0)···(x?xk?1)
andtheconnectionbetweenthenthdivideddi?erenceandnthderivativeoff.
Supposethatthedistinctnumbersx0,x1,/dots,xnaregiventogetherwiththevaluesoffandf?atthesenumbers.De?neanewsequencez0,z1,...,z2n+1by
z2i=z2i+1=xi,foreachi=0,1,...,n,
andconstructthedivideddi?erencetablethatusesz0,z1,....z2n+1
Sincez2i=z2i+1=xi,foreachi,wecannotde?nef[z2i,z2i+1]bythedivideddi?erenceformula.Ifweassumethatthereasonablesubstitutioninthissituationisf[z2i,z2i+1]=f?(z2i)=f?(xi),wecanusetheentries
f?(x0),f?(x1),...,f?(xn)
inplaceoftheunde?ned?rstdivideddi?erences
f[z0,z1],f[z2,z3],...,f[z2n,z2n+1]
Theremainingdivideddi?erencesareproducedasusual,andtheappropriatedivideddi?erencesareemployedinNewton’sinterpolatorydivided-di?erenceformula.
TheHermitepolynomialisgivenby
H2n+1(x)=f[z0]+2n+1?
k=1f[z0,...,xk](x?z0)(x?z1)...(x?zk?1)
CHAPTER3.HERMITEINTERPOLATION11
3.2
3.2.1Algorithmdescriptionpseudocode
Toobtainthecoe?cientsoftheHermiteinterpolatingpolynomialH(x)onthe(n+1)distinctnumbersx0,...,xnforthefunctionf:
INPUTnumbersx0,x1,...,xn;valuesf(x0),...,f(xn)andf?(x0),...,f?(xn)OUTPUTthenumbersQ0,0,Q1,1,...,Q2n+1,2n+1where
H(x)=Q0,0+Q1,1(x?x0)+Q2,2(x?x0)2+Q3,3(x?x0)2(x?x1)
+Q4,4(x?x0)2(x?x1)2+···
+Q2n+1,2n+1(x?x0)2(x?x1)2···(x?xn?1)2(x?xn)
Step1Fori=0,1,...,ndoStep2and3
Step2Setz2i=xi;
z2i+1=xi;
Q2i,0=f(xi);
Q2i+1,0=f(xi)
Q2i+1,1=f?(xi)
Step3Ifi=0thenset
2i,1=2i,0?Q2i?1,0
z2i?z2i?1
Step4Fori=2,3,...,2n+1
forj=2,3,...,iset
QQQ
i,j=i,j?1?i?1,j?1
zi?zi?j
Step5OUTPUT(Q0,0,Q1,1...Q2n+1,2n+1)
STOP
CHAPTER3.HERMITEINTERPOLATION12
3.2.2code
3.3
3.3.1NumericalexperimentsExample1
UsetheHermitepolynomialthatagreeswiththedatainTable3.1to?ndanapproximationoff(1.5)
Table3.1:Example1
k
2
3xk1.61.9f(xk)0.45540220.2818186f?(xk)?0.5698959?0.5811571
Table3.2showstheentriesthatareusedfordeterminingtheHermitepoly-nomialH5(x)forx0,x1,andx2.
TheentriesinTable3.3usethegivendata.
CHAPTER3.HERMITEINTERPOLATION13H5(1.5)=0.6200860+(1.5?1.3)(?0.5220232)+(1.5?1.3)2(?0.0897427)
+(1.5?1.3)2(1.5?1.6)(0.0663657)+(1.5?1.3)2(1.5?1.6)2(0.0026663)+(1.5?1.3)2(1.5?1.6)2(1.5?1.9)(?0.0027738)
=0.5118277
3.3.2Example2
UseHermiteinterpolationtoconstructanapproximatingpolynomialforthefollowingdataTheentriesinTable3.5usethegivendata.
H5(x)=?0.0247500+(x+0.5)(0.7510000)+(x+0.5)2(2.7510000)+(x+0.5)2(x+0.25)
CHAPTER3.HERMITEINTERPOLATION14
Table3.2:
00z1=x0z2=x1z3=x1z4=x2z5=x2
00f[z1]=f(x0)
f[z1,z2]=
f[z2]=f(x1)f[z3]=f(x1)
f[z3,z4]=
f[z4]=f(x2)f[z5]=f(x2)
f[z0,z1]=f?(x0)
f[z2]?f[z1]21?
di?erences
f[z0,z1,z2]f[z1,z2,z3]f[z2,z3,z4]f[z3,z4,z5]
f[z2,z3]=f(x1)
f[z4]?f[z3]43
f[z4,z5]=f?(x2)
di?erencesdi?erences
f[z0,z1,z2,z3]
f[z0,z1,z2,z3,z4]
f[z1,z2,z3,z4]
f[z1,z2,z3,z4,z5]
f[z2,z3,z4,z5]
f[z0,z1,z2,z3,z4,z5]
CHAPTER3.HERMITEINTERPOLATION15
Table3.3:
1.31.61.61.91.9
-0.5220232
0.6200860
-0.5489460
0.4554022
-0.5698959
0.4554022
-0.5786120
0.2818186
-0.5811571
0.2818186
-0.0084837-0.0290537
0.0685667
-0.0698330
0.0679655
0.0010020
-0.0897427
0.0663657
0.0026663
-0.0027738
Table3.4:Example2
k23
xk?0.250
f(xk)0.33493751.101000
f?(xk)2.18900004.0020000
Table3.5:
-0.5-0.25-0.2500
0.7510000
-0.0247500
1.4387500
0.3349375
2.1890000
0.3349375
3.0642500
1.1010000
4.0020000
1.1010000
3.75100003.5010000
1
3.0010000
1
2.7510000
1
Chapter4
CubicSplineInterpolationThepreviouschapterconcernedtheapproximationofarbitraryfunctionsonclosedintervalsbytheuseofpolynomials.However,theoscillatorynatureofhigh-degreepolynomialsandthepropertythata?uctuationoverasmallportionoftheintervalcaninducelarge?uctuationsovertheentireragerestrictstheiruse.
Analternativeapproachistodividetheintervalintoacollectionofsubin-tervalsandconstructa(generally)di?erentapproximatingpolynomialoneachsubinterval.Approximationbyfunctionsofthistypeiscalledpiecewise-polynomialapproximation
Themostcommonpiecewise-polynomialapproximationusescubicpolyno-mialsbetweeneachsuccessivepairofnodesandiscalledcubicsplinein-terpolation.Ageneralcubicpolynomialinvolvesfourconstants,sothereissu?cient?exibilityinthecubicsplineproceduretoensurethattheinterpolantisnotonlycontinuouslydi?erentiableontheinterval,butalsohasacontinuoussecondderivative.Theconstructionofthecubicsplinedoesnot,however,as-sumethatthederivativesoftheinterpolantagreewiththoseofthefunctionitisapproximating,evenatthenodes.
4.1Mathematicaldeduction
Givenafunctionfde?nedon[a,b]andasetofnodesa=x0<x1</cdots<xn=b,acubicsplineinterpolantSforfisafunctionthatsatis?esthefollowingconditions:
a.S(x)isacubicpolynomial,denotedSj(x),onthesubinterval[xj,xj+1]foreachj=0,1,...,n?1;
b.S(xj)=f(xj)foreachj=0,1,...,n;
c.Sj+1(xj+1)=Sj(xj+1)foreachj=0,1,...,n?2;
??d.Sj+1(xj+1)=Sj(xj+1)foreachj=0,1,...,n?2;
16
CHAPTER4.CUBICSPLINEINTERPOLATION
????e.Sj+1(xj+1)=Sj(xj+1)foreachj=0,1,...,n?2;17
f.Oneofthefollowingsetsofboundaryconditionsissatis?ed:
(1)S??(x0)=S??(xn)=0(freeornaturalboundary)
(2)S?(x0)=f?(x0)andS?(xn)=f?(xn(clampedboundary)
Althoughcubicsplinesarede?nedwithotherboundaryconditions,thecon-ditionsgivenin(f)aresu?cientforourpurposes.Whenthefreeboundaryconditionsoccur,thesplineiscalledanaturalspline,anditsgraphapproxi-matestheshapethatalong?exiblerodwouldassumeifforcedtogothroughthedatapoints{(x0,f(x0)),(x1,f(x1)),...,(xn,f(xn))}.Inthischapter,weonlyconsiderthisone
Toconstructthecubicsplineinterpolantforagivenfunctionf,thecondi-tionsinthede?nitionareappliedtothecubicpolynomials
Sj(x)=aj+bj(x?xj)+cj(x?xj)2+dj(x?xj)3
foreachj=0,1,...,n?1.
Since
Sj(xj)=aj=f(xj)
condition(c)canbeappliedtoobtain
aj+1=Sj+1(xj+1)=Sj(xj+1)=aj+bj(xj+1?xj)+cj(xj+1?xj)2+dj(xj+1?xj)3foreachj=0,1,...,n?2.
Sincethetermsxj+1?xjareusedrepeatedlyinthisdevelopment,itisconvenienttointroducethesimplernotation
hj=xj+1?xj
foreachj=0,1,...,n?1..Ifwealsode?nean=f(xn),thentheequation
3aj+1=aj+bjhj+cjh2j+djhj(4.1)
holdsforeachj=0,1,...,n?2
Inasimilarmanner,de?nebn=S?(xn)andobservethat
?Sj(x)=bj+2cj(x?xj)+3dj(x?xj)2
?impliesSj(xj)=bj,foreachj=0,1,...,n?1.Applyingcondition(d)gives
bj+1=bj+2cjhj+3djh2j,(4.2)
foreachj=0,1,...,n?2
Anotherrelationshipbetweenthecoe?cientsofSjisobtainedbyde?ningcn=S??(xn)/2andapplyingcondition(e).Then,foreachj=0,1,...,n?1,
cj+1=cj+3djhj(4.3)
CHAPTER4.CUBICSPLINEINTERPOLATION18
SolvingfordjinEq.(4.3)andsubstitutingthisvalueintoEqs.(4.1)and(4.2)gives,forj=0,1,...,n?1,thenewequations
aj+1
and
bj+1=bj+hj(cj+cj+1)(4.5)
The?nalrelationshipinvolvingthecoe?cientsisobtainedbysolvingtheappropriateequationintheformofequation(3.4),?rstforbj,
bj=hj1(aj+1?aj)?(2cj+cj+1)hj3(4.6)h2j=aj+bjhj+(2cj+cj+1)3(4.4)
andthen,withareductionoftheindex,forbj?1.Thisgives
bj?1=1
hj?1(aj?aj?1)?hj?1(2cj?1+cj),3
SubstitutingthesevaluesintotheequationderivedfromEq(4.5),withtheindexreducedbyone,givesthelinearsystemofequations.
hj?1cj?1+2(hj?1+hj)cj+hjcj+1=33(aj+1?aj)?(aj?aj?1)(4.7)hjhj?1
foreachj=1,2,...,n?1.Thissysteminvolvesonlythe{cj}nj=0asunknowns
n?1sincethevaluesof{hj}j=0and{aj}nj=0aregiven,respectively,bythespacing
nofthenodes{xj}j=0andthevaluesoffatthenodes.
Notethatoncethevaluesof{cj}nj=0aredetermined,itisasimplematterto
?1n?1?ndtheremainderoftheconstants{bj}nj=0fromEq.(4.6)and{dj}j=0from
?1Eq.(4.3),andtoconstructthecubicpolynomials{Sj(x)}nj=0.
Themajorquestionthatarisesinconnectionwiththisconstructioniswhetherthevaluesof{cj}nj=0canbefoundusingthesystemofequationsgiveninEq.(4.7)and,ifso,whetherthesevaluesareunique.Thefollowingtheoremsindicatethatthisisthecasewhenthefreeornaturalboundaryisimposed.Astheproofofthistheoremrequiresomeknowledgewehaven’tlearned,wedecidenottointroducetheprooftothisreport.
Theorem4.1Iffisde?nedata=x0<x1<···<xn=b,thenfhasauniquenaturalsplineinterpolantSonthenodesx0,x1,....xn;thatis,asplineinterpolantthatsatis?estheboundaryconditionsS??(a)=0andS??(b)=0.
4.2
4.2.1Algorithmdescriptionpseudocode
ToconstructthecubicsplineinterpolantSforthefunctionf,de?nedatthenumbersx0<x1<···<xn,satisfyingS??(x0)=S??(xn)=0:
CHAPTER4.CUBICSPLINEINTERPOLATIONINPUTn;x0,x1,...,xn;a0=f(x0),a1=f(x1),...,an=f(xn).OUTPUTaj,bj,cj,djforj=0,1,...,n?1.Step1Fori=0,1,...,n?1sethi=xi+1?xi.Step2Fori=1,...,n?1set
αi=Step3Setl0=1;
u0=0;
z0=0;
Step4Fori=1,2,...,n?1
setli=2(xi+1?xi?1)?hi?1ui?1;
ui=hi/li
zi=(αi?hi?1zi?1)/li
Step5Setln=1;
zn=0;
cn=0;
Step6Forj=n?1,n?2,...,0
setcj=zj?ujcj+1;
bj=(aj+1?aj)/hj?hj(cj+1+2cj)/3;
dj=(cj+1?cj)/(3hj).
Step7OUTPUT(aj,bj,cj,djforj=0,1,...,n?1)
STOP33(ai+1?ai)?(ai?ai?1)hihi?119
CHAPTER4.CUBICSPLINEINTERPOLATION20
4.2.2code
CHAPTER4.CUBICSPLINEINTERPOLATION21
4.3
4.3.1
Numericalexperiments
Example1
Table4.1:Example1
f(x)2.251.32.31.52.251.851.952.11.42.60.92.70.72.40.62.150.52.050.42.10.25
Usingthecodesabovetogeneratethefreecubicsplineforthisdataproducesthecoe?cientsshowninTable4.2.
Table4.2:
123xxxxxxxxxxxx3141516171819
j1.31.92.12.63.03.94.44.75.06.07.08.09.210.511.311.12.012.613.0
j1.51.852.12.62.72.42.152.052.12.252.32.251.951.40.90.70.60.50.4
j0.421.091.290.59-0.02-0.5-0.48-0.070.260.080.01-0.14-0.34-0.53-0.73-0.49-0.14-0.18-0.39
j-0.301.41-0.37-1.04-0.50-0.030.081.27-0.16-0.03-0.04-0.11-0.05-0.10-0.150.94-0.060.00-0.54
j0.95-2.96-0.450.450.170.081.31-1.580.040.00-0.020.02-0.01-0.021.21-0.840.04-0.450.60
4.3.2Example2
Constructthefreecubicsplineforthefollowingdata.
CHAPTER4.CUBICSPLINEINTERPOLATION22
Table4.3:Example2
0.2
0.3
0.4-0.283986680.006600950.24842440
Usingthecodesabovetogeneratethefreecubicsplineforthisdataproducesthecoe?cientsshownbelow.
Table4.4:
1
2j0.20.3j-0.28400.0066j3.18522.6171j-2.6987-2.9826j-0.94639.9421
Sincethecoe?cientshavebeendetermined,thepolynomialwillalsobearrivedateasily.
Chapter5
DiscussionandConclusionInthischapter,wewillanalyzeadvantagesandlimitationsofeachmethodre-spectively.
5.1InterpolationandtheLagrangePolynomialAmongthesemethods,theLagrangepolynomialisconsideredthesimplestone,meaningthatitneedstheleastworkload.However,astheLagrangepolynomialonlyrequiresthatthevaluesoftheinterpolatingpolynomialarethesamewiththoseoforiginalfunctiononthegivennodes,thereforeitsaccuracyisrelativelow,comparedwithHermitepolynomial.Moreover,ithastheinherentweaknessofoscillation,whichlimitsitsapplicationtosituationwherethenumberofnodesislarge.
5.2HermiteInterpolation
ComparedwiththeLagrangePolynomial,Hermitepolynomialinterpolateafunctionanditsderivativeatthenodes,thusitcanbeexpectedtobemoreaccurate.However,italsomeansthatmoreinformationaboutthefunctionbeingappropriatedwillberequired,whichlimitsitsapplicationtosituationswherenotenoughinformationabouttheoriginalpolynomialcanbeprovided.Andwhentherearealargeofnumberofnodes,theHermitepolynomialalsoexhibitoscillationweaknesses.
5.3CubicSplineInterpolation
Themostobviousadvantageofthisinterpolationisthatitsuccessfullysolvedtheinherentproblem,oscillatorynatureofhigh-degreepolynomial,withintheHermiteInterpolationandtheLagrangeInterpolation.However,theworkloadofthisinterpolationissomewhatheavierthanothers.
23
Bibliography
[1]RichardL.BurdenandJ.DouglasFaires:NumericalAnalysis,chapter3
(2001)
24
-
初中数学学习心得体会
数学是一们基础学科,我们从小学就开始接触到它。初中数学对知识的难度、深度、广度要求更高,有一部分同学由于不适应这种变化,数学成绩总…
-
数学学习总结
这次国培,我的感悟很多,也思考很多原来不曾想过的问题,同时收获也很多。“国培”期间,每一位专家们精彩的讲演,都使我很感动;他们结合…
-
数学学习总结
学习数学的意义数学有其内在的价值和意义,数学学习赋予了一个人成长意义上的本质力量。数学学习强烈而深远地影响着自我认识,数学跟语文不…
-
学习数学心得体会[1]
事只怕有心人我们每一个人都应认真对待平时的习惯不养好以后就会错误百出判案高手宋慈因一时疏忽造成了冤假错案的发生那更何况是我们呢所以…
-
高中数学学习心得体会
高中数学,可能对于某些人来说是一门头疼的课程。现在,我以毕业多年的身份来谈谈高中数学的学习心得体会,可能说法有些偏颇,但是都是我的…
-
数值分析学习总结感想
数值分析学习感想摘要数值分析主要介绍现代科学计算中常用的数值计算方法及其基本原理研究并解决数值问题的近似解是数学理论与计算机和实际…
-
数值分析第五章学习小结
第5章插值与逼近学习小结研1302学号一本章学习体会本章为插值与逼近是非常重要的一章插值与逼近都是指用某个简单的函数在满足一定的条…
-
数值分析学习报告
数值分析学习心得报告班级姓名学号学习数值分析的心得体会数值分析是一门利用计算机求解数学问题数值解的课程有很强的理论性和实践性无意中…
-
西南交通大学研究 数值分析上机实习报告20xx
数值分析上机实习报告要求1应提交一份完整的实习报告具体要求如下1要有封面封面上要标明姓名学号专业和联系电话2要有序言说明所用语言及…
-
数值分析学习报告
数值分析学习心得报告班级11级软工一班姓名学号20xx7610指导老师学习数值分析的心得体会无意中的一次选择让我接触了数值分析作为…
-
数值分析课程总结
课程内容1误差了解误差的来源与分类及误差的基本概念与性质;熟悉绝对误差及绝对误差限、相对误差及相对误差限和有效数字之间的关系;掌握…