圆锥曲线(椭圆,双曲线,抛物线)的定义、方程和性质知识总结
抛物线标准方程与几何性质
一、抛物线定义的理解
平面内与一个定点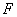 和一条定直线
和一条定直线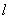 的距离相等的点的轨迹叫做抛物线,定点
的距离相等的点的轨迹叫做抛物线,定点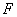 为抛物线的焦点,定直线
为抛物线的焦点,定直线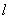 为抛物线的准线。
为抛物线的准线。
注:① 定义可归结为“一动三定”:一个动点设为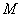 ;一定点
;一定点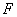 (即焦点);一定直线
(即焦点);一定直线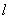 (即准线);一定值1(即动点
(即准线);一定值1(即动点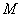 到定点
到定点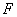 的距离与它到定直线
的距离与它到定直线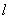 的距离之比1)
的距离之比1)
② 定义中的隐含条件:焦点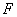 不在准线
不在准线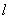 上。若
上。若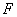 在
在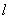 上,抛物线退化为过
上,抛物线退化为过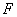 且垂直于
且垂直于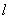 的一条直线
的一条直线
③ 圆锥曲线的统一定义:平面内与一定点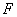 和定直线
和定直线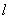 的距离之比为常数
的距离之比为常数 的点的轨迹,当
的点的轨迹,当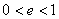 时,表示椭圆;当
时,表示椭圆;当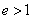 时,表示双曲线;当
时,表示双曲线;当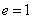 时,表示抛物线。
时,表示抛物线。
④ 抛物线定义建立了抛物线上的点、焦点、准线三者之间的距离关系,在解题中常将抛物线上的动点到焦点距离(称焦半径)与动点到准线距离互化,与抛物线的定义联系起来,通过这种转化使问题简单化。
二、抛物线标准方程
1.抛物线标准方程建系特点:以抛物线的顶点为坐标原点,对称轴为一条坐标轴建立直角坐标系,这样使标准方程不仅具有对称性,而且曲线过原点,方程不含常数项,形式更为简单,便于应用。
2.四种标准方程的联系与区别:由于选取坐标系时,该坐标轴有四种不同的方向,因此抛物线的标准方程有四种不同的形式。抛物线标准方程的四种形式为: ,
,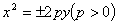 ,其中:
,其中:
① 参数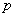 的几何意义:焦参数
的几何意义:焦参数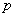 是焦点到准线的距离,所以
是焦点到准线的距离,所以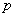 恒为正值;
恒为正值;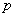 值越大,张口越大;
值越大,张口越大;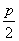 等于焦点到抛物线顶点的距离。
等于焦点到抛物线顶点的距离。
②标准方程的特点:方程的左边是某变量的平方项,右边是另一变量的一次项,方程右边一次项的变量与焦点所在坐标轴的名称相同,一次项系数的符号决定抛物线的开口方向,即对称轴为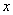 轴时,方程中的一次项变量就是
轴时,方程中的一次项变量就是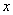 , 若
, 若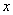 的一次项前符号为正,则开口向右,若
的一次项前符号为正,则开口向右,若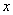 的一次项前符号为负,则开口向左;若对称轴为
的一次项前符号为负,则开口向左;若对称轴为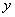 轴时,方程中的一次项变量就是
轴时,方程中的一次项变量就是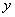 , 当
, 当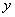 的一次项前符号为正,则开口向上,若
的一次项前符号为正,则开口向上,若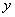 的一次项前符号为负,则开口向下。
的一次项前符号为负,则开口向下。
三、求抛物线标准方程
求抛物线方程时,要依据题设条件,弄清抛物线的对称轴和开口方向,正确地选择抛物线标准方程.
① 待定系数法:因抛物线标准方程有四种形式,若能确定抛物线的形式,需一个条件就能解出待定系数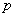 ,因此要做到“先定位,再定值”。
,因此要做到“先定位,再定值”。
注:当求顶点在原点,对称轴为坐标轴的抛物线时,若不知开口方向,可设为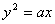 或
或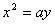 ,这样可避免讨论。
,这样可避免讨论。
② 抛物线轨迹法:若由已知得抛物线是标准形式,可直接设其标准式;若不确定是否是标准式,由已知条件可知曲线的动点的规律,一般用轨迹法求之。
四、抛物线的简单几何性质

注:① 焦点的非零坐标是一次项系数的 ;
;
② 对于不同形式的抛物线,位置不同,其性质也有所不同,应弄清它们的异同点,数形结合,掌握方程与有关特征量,有关性质间的对应关系,从整体上认识抛物线及其性质。
五、直线与抛物线有关问题
1.直线与抛物线的位置关系的判断:直线与抛物线方程联立方程组,消去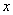 或
或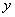 化得形如
化得形如 (*)的式子:
(*)的式子:
① 当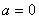 时,(*)式方程只有一解,即直线与抛物线只有一个交点,此时直线与抛物线不是相切,而是与抛物线对称轴平行或重合;
时,(*)式方程只有一解,即直线与抛物线只有一个交点,此时直线与抛物线不是相切,而是与抛物线对称轴平行或重合;
② 当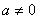 时,若△>0
时,若△>0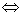 (*)式方程有两组不同的实数解
(*)式方程有两组不同的实数解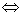 直线与抛物线相交;
直线与抛物线相交;
若△=0 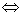 (*)式方程有两组相同的实数解
(*)式方程有两组相同的实数解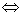 直线与抛物线相切;
直线与抛物线相切;
若△<0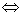 (*)式方程无实数解
(*)式方程无实数解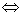 直线与抛物线相离.
直线与抛物线相离.
2.直线与抛物线相交的弦长问题
① 弦长公式:设直线交抛物线于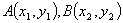 ,则
,则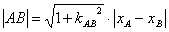
或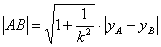 .
.
② 若直线与抛物线相交所得弦为焦点弦时,借助于焦半径公式处理:
抛物线 上一点
上一点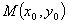 的焦半径长是
的焦半径长是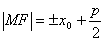 ,抛物线
,抛物线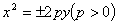 上一点
上一点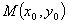 的焦半径长是
的焦半径长是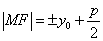
六、抛物线焦点弦的几个常用结论
设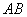 为过抛物线
为过抛物线 焦点的弦,设
焦点的弦,设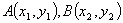 ,直线
,直线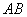 的倾斜角为
的倾斜角为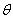 ,则
,则
① 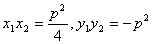 ;
;
② 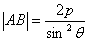
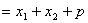 ;
;
③以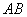 为直径的圆与准线相切;
为直径的圆与准线相切;
④弦两端点与顶点所成三角形的面积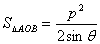 ;
;
⑤  ;
;
⑥ 焦点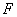 对
对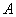 、
、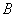 在准线上射影的张角为900;
在准线上射影的张角为900;
七、抛物线有关注意事项
1.凡涉及抛物线的弦长、弦的中点、弦的斜率问题时要注意利用韦达定理,采用“设而不求”或“点差法”等方法,能避免求交点坐标的复杂运算.同时在解决直线与抛物线相交问题时不能忽视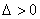 这个条件。
这个条件。
2.解决与抛物线的焦半径、焦点弦有关问题时,多从抛物线的定义出发,实现抛物线上任一点到焦点的距离和这点到准线的距离之间的相互转化,并应注意焦点弦的几何性质.
1.(2009宁夏海南卷理)设已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交于A,B两点。若AB的中点为(2,2),则直线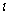 的方程为_____________.
的方程为_____________.
解析:抛物线的方程为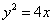 ,
,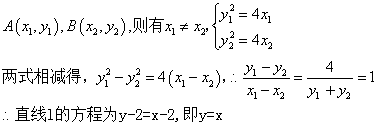
答案:y=x
2.(2009天津卷理)设抛物线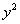 =2x的焦点为F,过点M(
=2x的焦点为F,过点M(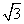 ,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,
,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,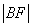 =2,则
=2,则 BCF与
BCF与 ACF的面积之比
ACF的面积之比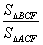 =
=
(A)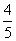 (B)
(B)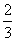 (C)
(C)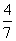 (D)
(D)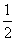
【考点定位】本小题考查抛物线的性质、三点共线的坐标关系,和综合运算数学的能力,中档题。
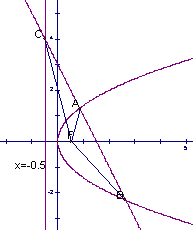
解析:由题知 ,
,
又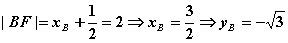
由A、B、M三点共线有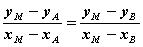 即
即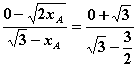 ,故
,故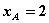 ,
, 
∴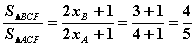 ,故选择A。
,故选择A。
3.(2009福建卷理)过抛物线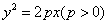 的焦点F作倾斜角为
的焦点F作倾斜角为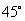 的直线交抛物线于A、B两点,若线段AB的长为8,则
的直线交抛物线于A、B两点,若线段AB的长为8,则 ________________
________________ 

【答案】:2
解析:由题意可知过焦点的直线方程为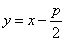 ,联立有
,联立有 ,又
,又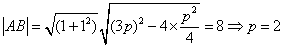 。
。
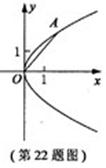 4.在平面直角坐标系
4.在平面直角坐标系 中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在
中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在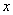 轴上。
轴上。
(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点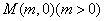 的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为
的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为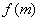 ,求
,求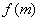 关于
关于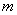 的表达式。
的表达式。
【解析】 [必做题]本小题主要考查直线、抛物线及两点间的距离公式等基本知识,考查运算求解能力。满分10分。

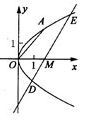

5.已知m是非零实数,抛物线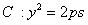 (p>0)
(p>0)
的焦点F在直线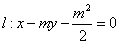 上。
上。
(I)若m=2,求抛物线C的方程
(II)设直线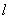 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A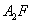 ,△
,△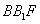 的重心分别为G,H
的重心分别为G,H
求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外。


7已知抛物线C: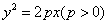 过点A (1 , -2)。
过点A (1 , -2)。
(I)求抛物线C 的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线L,使得直线L与抛物线C有公共点,且直线OA与L的距离等于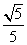 ?若存在,求直线L的方程;若不存在,说明理由。K^S*5U.C#O
?若存在,求直线L的方程;若不存在,说明理由。K^S*5U.C#O

(2010全国卷1理数)(21)(本小题满分12分)
已知抛物线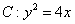 的焦点为F,过点
的焦点为F,过点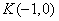 的直线
的直线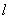 与
与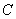 相交于
相交于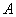 、
、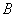 两点,点A关于
两点,点A关于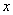 轴的对称点为D.
轴的对称点为D.
(Ⅰ)证明:点F在直线BD上;
(Ⅱ)设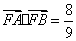 ,求
,求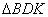 的内切圆M的方程 .
的内切圆M的方程 .



第二篇:解圆锥曲线问题常用方法+椭圆与双曲线的经典结论+椭圆与双曲线的对偶性质总结[1]
解圆锥曲线问题常用方法+椭圆与双曲线的经典结论+椭圆与双曲线的对偶性质总结
解圆锥曲线问题常用以下方法:
1、定义法
(1)椭圆有两种定义。第一定义中,r1+r2=2a。第二定义中,r1=ed1 r2=ed2。
(2)双曲线有两种定义。第一定义中,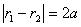 ,当r1>r2时,注意r2的最小值为c-a:第二定义中,r1=ed1,r2=ed2,尤其应注意第二定义的应用,常常将 半径与“点到准线距离”互相转化。
,当r1>r2时,注意r2的最小值为c-a:第二定义中,r1=ed1,r2=ed2,尤其应注意第二定义的应用,常常将 半径与“点到准线距离”互相转化。
(3)抛物线只有一种定义,而此定义的作用较椭圆、双曲线更大,很多抛物线问题用定义解决更直接简明。
2、韦达定理法
因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用。
3、解析几何的运算中,常设一些量而并不解解出这些量,利用这些量过渡使问题得以解决,这种方法称为“设而不求法”。设而不求法对于直线与圆锥曲线相交而产生的弦中点问题,常用“点差法”,即设弦的两个端点A(x1,y1),B(x2,y2),弦AB中点为M(x0,y0),将点A、B坐标代入圆锥曲线方程,作差后,产生弦中点与弦斜率的关系,这是一种常见的“设而不求”法,具体有:
(1)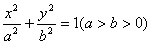 与直线相交于A、B,设弦AB中点为M(x0,y0),则有
与直线相交于A、B,设弦AB中点为M(x0,y0),则有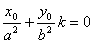 。
。
(2)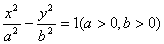 与直线l相交于A、B,设弦AB中点为M(x0,y0)则有
与直线l相交于A、B,设弦AB中点为M(x0,y0)则有
(3)y2=2px(p>0)与直线l相交于A、B设弦AB中点为M(x0,y0),则有2y0k=2p,即y0k=p.
【典型例题】
例1、(1)抛物线C:y2=4x上一点P到点A(3,4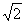 )与到准线的距离和最小,则点 P的坐标为______________
)与到准线的距离和最小,则点 P的坐标为______________
(2)抛物线C: y2=4x上一点Q到点B(4,1)与到焦点F的距离和最小,则点Q的坐标为 。
 分析:(1)A在抛物线外,如图,连PF,则
分析:(1)A在抛物线外,如图,连PF,则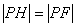 ,因而易发现,当A、P、F三点共线时,距离和最小。
,因而易发现,当A、P、F三点共线时,距离和最小。
(2)B在抛物线内,如图,作QR⊥l交于R,则当B、Q、R三点共线时,距离和最小。
解:(1)(2,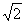 )
)
连PF,当A、P、F三点共线时,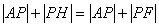 最小,此时AF的方程为
最小,此时AF的方程为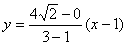 即 y=2
即 y=2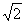 (x-1),代入y2=4x得P(2,2
(x-1),代入y2=4x得P(2,2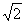 ),(注:另一交点为(
),(注:另一交点为(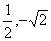 ),它为直线AF与抛物线的另一交点,舍去)
),它为直线AF与抛物线的另一交点,舍去)
(2)(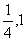 )
)
过Q作QR⊥l交于R,当B、Q、R三点共线时, 最小,此时Q点的纵坐标为1,代入y2=4x得x=
最小,此时Q点的纵坐标为1,代入y2=4x得x=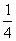 ,∴Q(
,∴Q(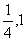 )
)
点评:这是利用定义将“点点距离”与“点线距离”互相转化的一个典型例题,请仔细体会。
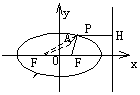 例2、F是椭圆
例2、F是椭圆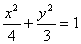 的右焦点,A(1,1)为椭圆内一定点,P为椭圆上一动点。
的右焦点,A(1,1)为椭圆内一定点,P为椭圆上一动点。
(1)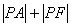 的最小值为
的最小值为
(2) 的最小值为
的最小值为
分析:PF为椭圆的一个焦半径,常需将另一焦半径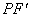 或准线作出来考虑问题。
或准线作出来考虑问题。
解:(1)4-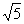
设另一焦点为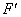 ,则
,则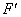 (-1,0)连A
(-1,0)连A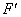 ,P
,P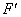
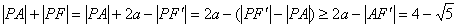
当P是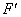 A的延长线与椭圆的交点时,
A的延长线与椭圆的交点时, 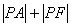 取得最小值为4-
取得最小值为4-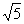 。
。
(2)3
作出右准线l,作PH⊥l交于H,因a2=4,b2=3,c2=1, a=2,c=1,e= ,
,
∴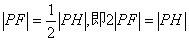
∴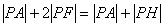
当A、P、H三点共线时,其和最小,最小值为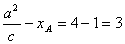
例3、动圆M与圆C1:(x+1)2+y2=36内切,与圆C2:(x-1)2+y2=4外切,求圆心M的轨迹方程。
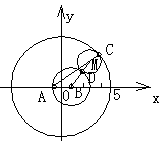 分析:作图时,要注意相切时的“图形特征”:两个圆心与切点这三点共线(如图中的A、M、C共线,B、D、M共线)。列式的主要途径是动圆的“半径等于半径”(如图中的
分析:作图时,要注意相切时的“图形特征”:两个圆心与切点这三点共线(如图中的A、M、C共线,B、D、M共线)。列式的主要途径是动圆的“半径等于半径”(如图中的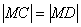 )。
)。
解:如图,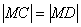 ,
,
∴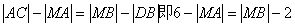
∴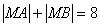 (*)
(*)
∴点M的轨迹为椭圆,2a=8,a=4,c=1,b2=15轨迹方程为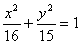
点评:得到方程(*)后,应直接利用椭圆的定义写出方程,而无需再用距离公式列式求解,即列出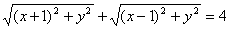 ,再移项,平方,…相当于将椭圆标准方程推导了一遍,较繁琐!
,再移项,平方,…相当于将椭圆标准方程推导了一遍,较繁琐!
例4、△ABC中,B(-5,0),C(5,0),且sinC-sinB=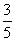 sinA,求点A的轨迹方程。
sinA,求点A的轨迹方程。
分析:由于sinA、sinB、sinC的关系为一次齐次式,两边乘以2R(R为外接圆半径),可转化为边长的关系。
解:sinC-sinB=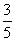 sinA 2RsinC-2RsinB=
sinA 2RsinC-2RsinB=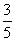 ·2RsinA
·2RsinA
∴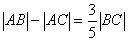
即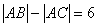 (*)
(*)
∴点A的轨迹为双曲线的右支(去掉顶点)
∵2a=6,2c=10
∴a=3, c=5, b=4
所求轨迹方程为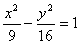 (x>3)
(x>3)
点评:要注意利用定义直接解题,这里由(*)式直接用定义说明了轨迹(双曲线右支)
例5、定长为3的线段AB的两个端点在y=x2上移动,AB中点为M,求点M到x轴的最短距离。
分析:(1)可直接利用抛物线设点,如设A(x1,x12),B(x2,X22),又设AB中点为M(x0y0)用弦长公式及中点公式得出y0关于x0的函数表达式,再用函数思想求出最短距离。
(2)M到x轴的距离是一种“点线距离”,可先考虑M到准线的距离,想到用定义法。
解法一:设A(x1,x12),B(x2,x22),AB中点M(x0,y0)
 则
则
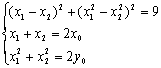
由①得(x1-x2)2[1+(x1+x2)2]=9
即[(x1+x2)2-4x1x2]·[1+(x1+x2)2]=9 ④
由②、③得2x1x2=(2x0)2-2y0=4x02-2y0
代入④得 [(2x0)2-(8x02-4y0)]·[1+(2x0)2]=9
∴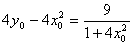 ,
,
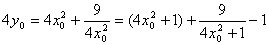
≥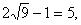
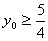
当4x02+1=3 即 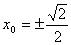 时,
时,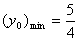 此时
此时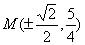
法二:如图,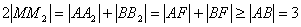
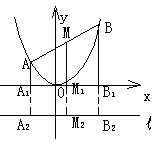 ∴
∴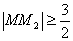 , 即
, 即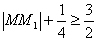 ,
,
∴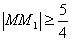 , 当AB经过焦点F时取得最小值。
, 当AB经过焦点F时取得最小值。
∴M到x轴的最短距离为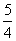
点评:解法一是列出方程组,利用整体消元思想消x1,x2,从而形成y0关于x0的函数,这是一种“设而不求”的方法。而解法二充分利用了抛物线的定义,巧妙地将中点M到x轴的距离转化为它到准线的距离,再利用梯形的中位线,转化为A、B到准线的距离和,结合定义与三角形中两边之和大于第三边(当三角形“压扁”时,两边之和等于第三边)的属性,简捷地求解出结果的,但此解法中有缺点,即没有验证AB是否能经过焦点F,而且点M的坐标也不能直接得出。
例6、已知椭圆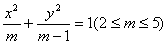 过其左焦点且斜率为1的直线与椭圆及准线从左到右依次变于A、B、C、D、设f(m)=
过其左焦点且斜率为1的直线与椭圆及准线从左到右依次变于A、B、C、D、设f(m)=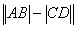 ,(1)求f(m),(2)求f(m)的最值。
,(1)求f(m),(2)求f(m)的最值。
分析:此题初看很复杂,对f(m)的结构不知如何运算,因A、B来源于“不同系统”,A在准线上,B在椭圆上,同样C在椭圆上,D在准线上,可见直接求解较繁,将这些线段“投影”到x轴上,立即可得防
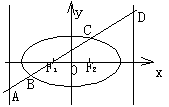
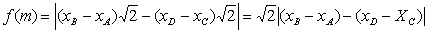
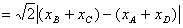

此时问题已明朗化,只需用韦达定理即可。
解:(1)椭圆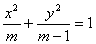 中,a2=m,b2=m-1,c2=1,左焦点F1(-1,0)
中,a2=m,b2=m-1,c2=1,左焦点F1(-1,0)
则BC:y=x+1,代入椭圆方程即(m-1)x2+my2-m(m-1)=0
得(m-1)x2+m(x+1)2-m2+m=0
∴(2m-1)x2+2mx+2m-m2=0
设B(x1,y1),C(x2,y2),则x1+x2=-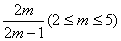
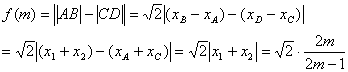
(2)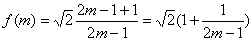
∴当m=5时,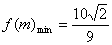
当m=2时,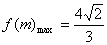
点评:此题因最终需求 ,而BC斜率已知为1,故可也用“点差法”设BC中点为M(x0,y0),通过将B、C坐标代入作差,得
,而BC斜率已知为1,故可也用“点差法”设BC中点为M(x0,y0),通过将B、C坐标代入作差,得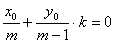 ,将y0=x0+1,k=1代入得
,将y0=x0+1,k=1代入得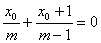 ,∴
,∴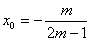 ,可见
,可见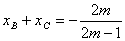
当然,解本题的关键在于对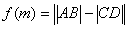 的认识,通过线段在x轴的“投影”发现
的认识,通过线段在x轴的“投影”发现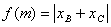 是解此题的要点。
是解此题的要点。
【同步练习】
1、已知:F1,F2是双曲线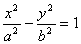 的左、右焦点,过F1作直线交双曲线左支于点A、B,若
的左、右焦点,过F1作直线交双曲线左支于点A、B,若 ,△ABF2的周长为( )
,△ABF2的周长为( )
A、4a B、4a+m C、4a+2m D、4a-m
2、若点P到点F(4,0)的距离比它到直线x+5=0的距离小1,则P点的轨迹方程是
( )
A、y2=-16x B、y2=-32x C、y2=16x D、y2=32x
3、已知△ABC的三边AB、BC、AC的长依次成等差数列,且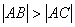 ,点B、C的坐标分别为(-1,0),(1,0),则顶点A的轨迹方程是( )
,点B、C的坐标分别为(-1,0),(1,0),则顶点A的轨迹方程是( )
A、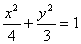 B、
B、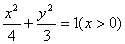
C、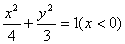 D、
D、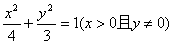
4、过原点的椭圆的一个焦点为F(1,0),其长轴长为4,则椭圆中心的轨迹方程是
( )
A、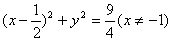 B、
B、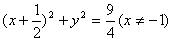
C、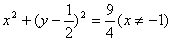 D、
D、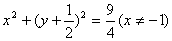
5、已知双曲线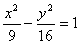 上一点M的横坐标为4,则点M到左焦点的距离是
上一点M的横坐标为4,则点M到左焦点的距离是
6、抛物线y=2x2截一组斜率为2的平行直线,所得弦中点的轨迹方程是
7、已知抛物线y2=2x的弦AB所在直线过定点p(-2,0),则弦AB中点的轨迹方程是
8、过双曲线x2-y2=4的焦点且平行于虚轴的弦长为
9、直线y=kx+1与双曲线x2-y2=1的交点个数只有一个,则k=
10、设点P是椭圆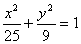 上的动点,F1,F2是椭圆的两个焦点,求sin∠F1PF2的最大值。
上的动点,F1,F2是椭圆的两个焦点,求sin∠F1PF2的最大值。
11、已知椭圆的中心在原点,焦点在x轴上,左焦点到坐标原点、右焦点、右准线的距离依次成等差数列,若直线l与此椭圆相交于A、B两点,且AB中点M为(-2,1),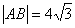 ,求直线l的方程和椭圆方程。
,求直线l的方程和椭圆方程。
12、已知直线l和双曲线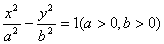 及其渐近线的交点从左到右依次为A、B、C、D。求证:
及其渐近线的交点从左到右依次为A、B、C、D。求证: 。
。
【参考答案】
1、C
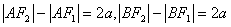 ,
,
∴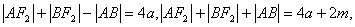 选C
选C
2、C
点P到F与到x+4=0等距离,P点轨迹为抛物线 p=8开口向右,则方程为y2=16x,选C
3、D
∵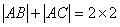 ,且
,且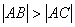
∵点A的轨迹为椭圆在y轴右方的部分、又A、B、C三点不共线,即y≠0,故选D。
4、A
设中心为(x,y),则另一焦点为(2x-1,2y),则原点到两焦点距离和为4得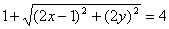 ,∴
,∴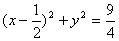
①又c<a,∴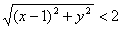
∴(x-1)2+y2<4 ②,由①,②得x≠-1,选A
5、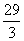
左准线为x=-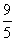 ,M到左准线距离为
,M到左准线距离为 则M到左焦点的距离为
则M到左焦点的距离为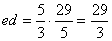
6、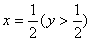
设弦为AB,A(x1,y1),B(x2,y2)AB中点为(x,y),则y1=2x12,y2=2x22,y1-y2=2(x12-x22)
∴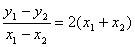 ∴2=2·2x,
∴2=2·2x,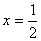
将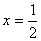 代入y=2x2得
代入y=2x2得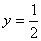 ,轨迹方程是
,轨迹方程是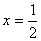 (y>
(y> )
)
7、y2=x+2(x>2)
设A(x1,y1),B(x2,y2),AB中点M(x,y),则
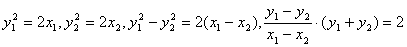
∵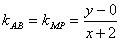 ,∴
,∴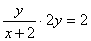 ,即y2=x+2
,即y2=x+2
又弦中点在已知抛物线内P,即y2<2x,即x+2<2x,∴x>2
8、4
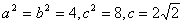 ,令
,令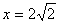 代入方程得8-y2=4
代入方程得8-y2=4
∴y2=4,y=±2,弦长为4
9、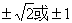
y=kx+1代入x2-y2=1得x2-(kx+1)2-1=0
∴(1-k2)x2-2kx-2=0
①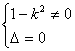 得4k2+8(1-k2)=0,k=
得4k2+8(1-k2)=0,k=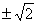
②1-k2=0得k=±1
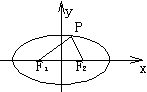 10、解:a2=25,b2=9,c2=16
10、解:a2=25,b2=9,c2=16
 设F
1、F
2为左、右焦点,则F
1(-4,0)F
2(4,0)
设F
1、F
2为左、右焦点,则F
1(-4,0)F
2(4,0)
设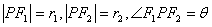
则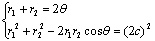
①2-②得2r1r2(1+cosθ)=4b2
∴1+cosθ=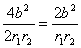 ∵r1+r2
∵r1+r2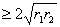 , ∴r1r2的最大值为a2
, ∴r1r2的最大值为a2
∴1+cosθ的最小值为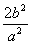 ,即1+cosθ
,即1+cosθ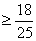
cosθ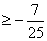 ,
, 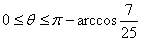 则当
则当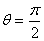 时,sinθ取值得最大值1,
时,sinθ取值得最大值1,
即sin∠F1PF2的最大值为1。
11、设椭圆方程为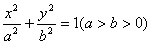
由题意:C、2C、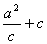 成等差数列,
成等差数列,
∴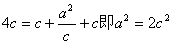 ,
,
∴a2=2(a2-b22DDFFF2+2222222大案要案 000),∴a2=2b2
椭圆方程为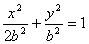 ,设A(x1,y1),B(x2,y2)
,设A(x1,y1),B(x2,y2)
则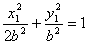 ①
① 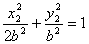 ②
②
①-②得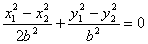
2222222∴
即 ∴k=1
∴k=1
直线AB方程为y-1=x+2即y=x+3, 代入椭圆方程即x2+2y2-2b2=0得x2+2(x+3)2-2b2=0
∴3x2+12x+18-2b2=0, 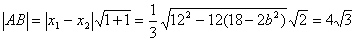
解得b2=12, ∴椭圆方程为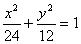 ,直线l方程为x-y+3=0
,直线l方程为x-y+3=0
12、证明:设A(x1,y1),D(x2,y2),AD中点为M(x0,y0)直线l的斜率为k,则

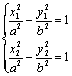 ①-②得
①-②得
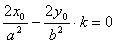 ③
③
设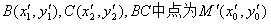 ,
,
 则
则
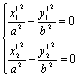
④-⑤得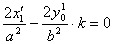 ⑥
⑥
由③、⑥知M、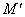 均在直线
均在直线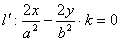 上,而M、
上,而M、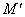 又在直线l上 ,
又在直线l上 ,
若l过原点,则B、C重合于原点,命题成立
若l与x轴垂直,则由对称性知命题成立
若l不过原点且与x轴不垂直,则M与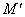 重合
重合
∴
椭圆与双曲线的对偶性质总结
椭 圆
1. 点P处的切线PT平分△PF1F2在点P处的外角.
2. PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.
3. 以焦点弦PQ为直径的圆必与对应准线相离.
4. 以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.
5. 若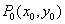 在椭圆
在椭圆 上,则过
上,则过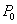 的椭圆的切线方程是
的椭圆的切线方程是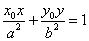 .
.
6. 若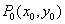 在椭圆
在椭圆 外 ,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是
外 ,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是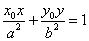 .
.
7. 椭圆 (a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点
(a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点 ,则椭圆的焦点角形的面积为
,则椭圆的焦点角形的面积为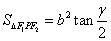 .
.
8. 椭圆 (a>b>0)的焦半径公式:
(a>b>0)的焦半径公式:
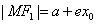 ,
,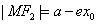 (
(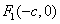 ,
, 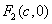
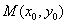 ).
).
9. 设过椭圆焦点F作直线与椭圆相交 P、Q两点,A为椭圆长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的椭圆准线于M、N两点,则MF⊥NF.
10. 过椭圆一个焦点F的直线与椭圆交于两点P、Q, A1、A2为椭圆长轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.
11. AB是椭圆 的不平行于对称轴的弦,M
的不平行于对称轴的弦,M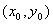 为AB的中点,则
为AB的中点,则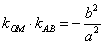 ,
,
即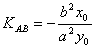 。
。
12. 若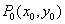 在椭圆
在椭圆 内,则被Po所平分的中点弦的方程是
内,则被Po所平分的中点弦的方程是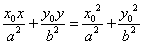 .
.
13. 若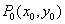 在椭圆
在椭圆 内,则过Po的弦中点的轨迹方程是
内,则过Po的弦中点的轨迹方程是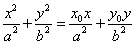 .
.
双曲线
1. 点P处的切线PT平分△PF1F2在点P处的内角.
2. PT平分△PF1F2在点P处的内角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.
3. 以焦点弦PQ为直径的圆必与对应准线相交.
4. 以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P在右支;外切:P在左支)
5. 若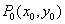 在双曲线
在双曲线 (a>0,b>0)上,则过
(a>0,b>0)上,则过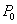 的双曲线的切线方程是
的双曲线的切线方程是 .
.
6. 若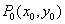 在双曲线
在双曲线 (a>0,b>0)外 ,则过Po作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是
(a>0,b>0)外 ,则过Po作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是 .
.
7. 双曲线 (a>0,b>o)的左右焦点分别为F1,F 2,点P为双曲线上任意一点
(a>0,b>o)的左右焦点分别为F1,F 2,点P为双曲线上任意一点 ,则双曲线的焦点角形的面积为
,则双曲线的焦点角形的面积为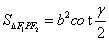 .
.
8. 双曲线 (a>0,b>o)的焦半径公式:(
(a>0,b>o)的焦半径公式:(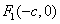 ,
, 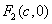
当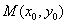 在右支上时,
在右支上时, ,
,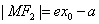 .
.
当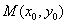 在左支上时,
在左支上时, ,
,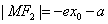
9. 设过双曲线焦点F作直线与双曲线相交 P、Q两点,A为双曲线长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的双曲线准线于M、N两点,则MF⊥NF.
10. 过双曲线一个焦点F的直线与双曲线交于两点P、Q, A1、A2为双曲线实轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.
11. AB是双曲线 (a>0,b>0)的不平行于对称轴的弦,M
(a>0,b>0)的不平行于对称轴的弦,M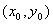 为AB的中点,则
为AB的中点,则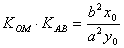 ,即
,即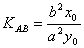 。
。
12. 若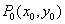 在双曲线
在双曲线 (a>0,b>0)内,则被Po所平分的中点弦的方程是
(a>0,b>0)内,则被Po所平分的中点弦的方程是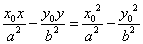 .
.
13. 若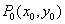 在双曲线
在双曲线 (a>0,b>0)内,则过Po的弦中点的轨迹方程是
(a>0,b>0)内,则过Po的弦中点的轨迹方程是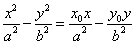 .
.
椭圆与双曲线的经典结论
椭 圆
1. 椭圆 (a>b>o)的两个顶点为
(a>b>o)的两个顶点为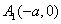 ,
,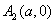 ,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程是
,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程是 .
.
2. 过椭圆 (a>0, b>0)上任一点
(a>0, b>0)上任一点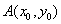 任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且
任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且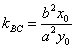 (常数).
(常数).
3. 若P为椭圆 (a>b>0)上异于长轴端点的任一点,F1, F 2是焦点,
(a>b>0)上异于长轴端点的任一点,F1, F 2是焦点, 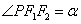 ,
, 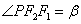 ,则
,则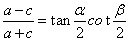 .
.
4. 设椭圆 (a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记
(a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记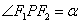 ,
, 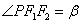 ,
,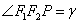 ,则有
,则有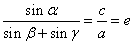 .
.
5. 若椭圆 (a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当0<e≤
(a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当0<e≤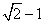 时,可在椭圆上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
时,可在椭圆上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
6. P为椭圆 (a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则
(a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则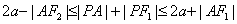 ,当且仅当
,当且仅当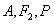 三点共线时,等号成立.
三点共线时,等号成立.
7. 椭圆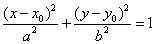 与直线
与直线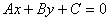 有公共点的充要条件是
有公共点的充要条件是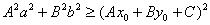 .
.
8. 已知椭圆 (a>b>0),O为坐标原点,P、Q为椭圆上两动点,且
(a>b>0),O为坐标原点,P、Q为椭圆上两动点,且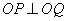 .(1)
.(1)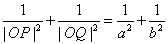 ;(2)|OP|2+|OQ|2的最大值为
;(2)|OP|2+|OQ|2的最大值为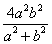 ;(3)
;(3)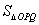 的最小值是
的最小值是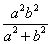 .
.
9. 过椭圆 (a>b>0)的右焦点F作直线交该椭圆右支于M,N两点,弦MN的垂直平分线交x轴于P,则
(a>b>0)的右焦点F作直线交该椭圆右支于M,N两点,弦MN的垂直平分线交x轴于P,则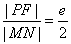 .
.
10. 已知椭圆 ( a>b>0) ,A、B、是椭圆上的两点,线段AB的垂直平分线与x轴相交于点
( a>b>0) ,A、B、是椭圆上的两点,线段AB的垂直平分线与x轴相交于点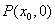 , 则
, 则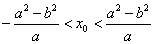 .
.
11. 设P点是椭圆 ( a>b>0)上异于长轴端点的任一点,F1、F2为其焦点记
( a>b>0)上异于长轴端点的任一点,F1、F2为其焦点记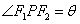 ,则(1)
,则(1) .(2)
.(2) 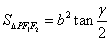 .
.
12. 设A、B是椭圆 ( a>b>0)的长轴两端点,P是椭圆上的一点,
( a>b>0)的长轴两端点,P是椭圆上的一点,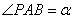 ,
,  ,
,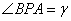 ,c、e分别是椭圆的半焦距离心率,则有(1)
,c、e分别是椭圆的半焦距离心率,则有(1)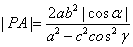 .(2)
.(2) 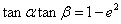 .(3)
.(3)  .
.
13. 已知椭圆 ( a>b>0)的右准线
( a>b>0)的右准线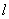 与x轴相交于点
与x轴相交于点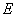 ,过椭圆右焦点
,过椭圆右焦点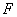 的直线与椭圆相交于A、B两点,点
的直线与椭圆相交于A、B两点,点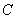 在右准线
在右准线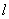 上,且
上,且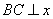 轴,则直线AC经过线段EF 的中点.
轴,则直线AC经过线段EF 的中点.
14. 过椭圆焦半径的端点作椭圆的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.
15. 过椭圆焦半径的端点作椭圆的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.
16. 椭圆焦三角形中,内点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).
(注:在椭圆焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点.)
17. 椭圆焦三角形中,内心将内点与非焦顶点连线段分成定比e.
18. 椭圆焦三角形中,半焦距必为内、外点到椭圆中心的比例中项.
双曲线
1. 双曲线 (a>0,b>0)的两个顶点为
(a>0,b>0)的两个顶点为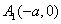 ,
,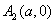 ,与y轴平行的直线交双曲线于P1、P2时A1P1与A2P2交点的轨迹方程是
,与y轴平行的直线交双曲线于P1、P2时A1P1与A2P2交点的轨迹方程是 .
.
2. 过双曲线 (a>0,b>o)上任一点
(a>0,b>o)上任一点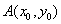 任意作两条倾斜角互补的直线交双曲线于B,C两点,则直线BC有定向且
任意作两条倾斜角互补的直线交双曲线于B,C两点,则直线BC有定向且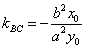 (常数).
(常数).
3. 若P为双曲线 (a>0,b>0)右(或左)支上除顶点外的任一点,F1, F 2是焦点,
(a>0,b>0)右(或左)支上除顶点外的任一点,F1, F 2是焦点, 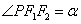 ,
, 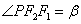 ,则
,则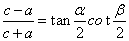 (或
(或 ).
).
4. 设双曲线 (a>0,b>0)的两个焦点为F1、F2,P(异于长轴端点)为双曲线上任意一点,在△PF1F2中,记
(a>0,b>0)的两个焦点为F1、F2,P(异于长轴端点)为双曲线上任意一点,在△PF1F2中,记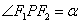 ,
, 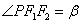 ,
,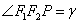 ,则有
,则有 .
.
5. 若双曲线 (a>0,b>0)的左、右焦点分别为F1、F2,左准线为L,则当1<e≤
(a>0,b>0)的左、右焦点分别为F1、F2,左准线为L,则当1<e≤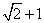 时,可在双曲线上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
时,可在双曲线上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
6. P为双曲线 (a>0,b>0)上任一点,F1,F2为二焦点,A为双曲线内一定点,则
(a>0,b>0)上任一点,F1,F2为二焦点,A为双曲线内一定点,则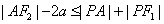 ,当且仅当
,当且仅当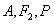 三点共线且
三点共线且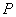 和
和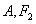 在y轴同侧时,等号成立.
在y轴同侧时,等号成立.
7. 双曲线 (a>0,b>0)与直线
(a>0,b>0)与直线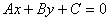 有公共点的充要条件是
有公共点的充要条件是 .
.
8. 已知双曲线 (b>a >0),O为坐标原点,P、Q为双曲线上两动点,且
(b>a >0),O为坐标原点,P、Q为双曲线上两动点,且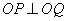 .
.
(1)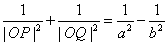 ;(2)|OP|2+|OQ|2的最小值为
;(2)|OP|2+|OQ|2的最小值为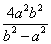 ;(3)
;(3)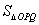 的最小值是
的最小值是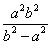 .
.
9. 过双曲线 (a>0,b>0)的右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于P,则
(a>0,b>0)的右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于P,则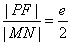 .
.
10. 已知双曲线 (a>0,b>0),A、B是双曲线上的两点,线段AB的垂直平分线与x轴相交于点
(a>0,b>0),A、B是双曲线上的两点,线段AB的垂直平分线与x轴相交于点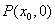 , 则
, 则 或
或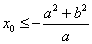 .
.
11. 设P点是双曲线 (a>0,b>0)上异于实轴端点的任一点,F1、F2为其焦点记
(a>0,b>0)上异于实轴端点的任一点,F1、F2为其焦点记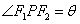 ,则(1)
,则(1)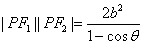 .(2)
.(2) 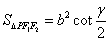 .
.
12. 设A、B是双曲线 (a>0,b>0)的长轴两端点,P是双曲线上的一点,
(a>0,b>0)的长轴两端点,P是双曲线上的一点,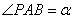 ,
,  ,
,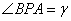 ,c、e分别是双曲线的半焦距离心率,则有(1)
,c、e分别是双曲线的半焦距离心率,则有(1)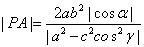 .
.
(2) 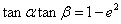 .(3)
.(3) 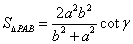 .
.
13. 已知双曲线 (a>0,b>0)的右准线
(a>0,b>0)的右准线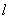 与x轴相交于点
与x轴相交于点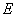 ,过双曲线右焦点
,过双曲线右焦点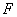 的直线与双曲线相交于A、B两点,点
的直线与双曲线相交于A、B两点,点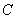 在右准线
在右准线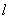 上,且
上,且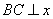 轴,则直线AC经过线段EF 的中点.
轴,则直线AC经过线段EF 的中点.
14. 过双曲线焦半径的端点作双曲线的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.
15. 过双曲线焦半径的端点作双曲线的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.
16. 双曲线焦三角形中,外点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).
(注:在双曲线焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点).
17. 双曲线焦三角形中,其焦点所对的旁心将外点与非焦顶点连线段分成定比e.
18. 双曲线焦三角形中,半焦距必为内、外点到双曲线中心的比例中项.
-
抛物线经典性质总结
1243y1y2p24AC39B905A39FB39906ABxp2p1x2p2x32sin2711AFBF2P8AOB39三点共…
-
抛物线常用性质总结
结论一若AB是抛物线y22pxp0的焦点弦过焦点的弦且Ax1y1Bx2y2则p2x1x24y1y2p2结论二已知直线AB是过抛物线…
-
抛物线经典性质总结
p2p2sin26ABx1x2p2x37112AFBFP398AOB三点共线9BOA三点共线39P210SAOB2sinS2AOB…
-
抛物线经典性质总结
2x1x243y1y2p24AC39B905A39FB39906ABxp2xp1x2322psin271AF1BF2P8AOB39…
-
抛物线经典性质总结
4112AFBFP39395AOB三点共线6BOA三点共线P27SAOB2sinS2AOBP83定值AB2PP9AFBF1cos1…
-
抛物线经典性质总结
1243y1y2p24AC39B905A39FB39906ABxp2p1x2p2x32sin2711AFBF2P8AOB39三点共…
-
抛物线常用性质总结
结论一若AB是抛物线y22pxp0的焦点弦过焦点的弦且Ax1y1Bx2y2则p2x1x24y1y2p2结论二已知直线AB是过抛物线…
-
抛物线焦点弦性质总结30条
基础回顾1以AB2345p2x1x24y1y2p2AC39B90A39FB3990p2p2sin26ABx1x2p2x37112A…
-
抛物线经典性质总结
p2p2sin26ABx1x2p2x37112AFBFP398AOB三点共线9BOA三点共线39P210SAOB2sinS2AOB…
-
抛物线经典性质总结
2x1x243y1y2p24AC39B905A39FB39906ABxp2xp1x2322psin271AF1BF2P8AOB39…
-
抛物线知识点归纳总结
抛物线知识点总结1.直线与抛物线的位置关系直线,抛物线,,消y得:(1)当k=0时,直线l与抛物线的对称轴平行,有一个交点;(2)…