正反比例函数和一次函数二次函数知识点汇总
正比例函数和一次函数
1、正比例函数和一次函数的概念
一般地,如果 (k,b是常数,k
(k,b是常数,k 0),那么y叫做x的一次函数。
0),那么y叫做x的一次函数。
特别地,当一次函数 中的b为0时,
中的b为0时, (k为常数,k
(k为常数,k 0)。这时,y叫做x的正比例函数。
0)。这时,y叫做x的正比例函数。
2、一次函数的图像
所有一次函数的图像都是一条直线
3、一次函数、正比例函数图像的主要特征:
一次函数 的图像是经过点(0,b)的直线;正比例函数
的图像是经过点(0,b)的直线;正比例函数 的图像是经过原点(0,0)的直线
的图像是经过原点(0,0)的直线


一次函数
(1) 一次函数的性质:y=kx+b(k、b为常数,k ≠0)当k >0时,y的值随x的值增大而增大;
当k<0时,y的值随x值的增大而减小.
⑷.直线y=kx+b(k、b为常数,k ≠0)时在坐标平面内的位置与k在的关系.
① 直线经过第一、二、三象限(直线不经过第四象限);
直线经过第一、二、三象限(直线不经过第四象限);
② 直线经过第一、三、四象限(直线不经过第二象限);
直线经过第一、三、四象限(直线不经过第二象限);
③ 直线经过第一、二、四象限(直线不经过第三象限);
直线经过第一、二、四象限(直线不经过第三象限);
④ 直线经过第二、三、四象限(直线不经过第一象限
直线经过第二、三、四象限(直线不经过第一象限
正比例函数
4、正比例函数的性质
一般地,正比例函数 有下列性质:
有下列性质:
(1)当k>0时,图像经过第一、三象限,y随x的增大而增大;
(2)当k<0时,图像经过第二、四象限,y随x的增大而减小。
反比例函数
(1)反比例函数
如果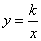 (k是常数,k≠0),那么y叫做x的反比例函数.
(k是常数,k≠0),那么y叫做x的反比例函数.
(2)反比例函数的图象
反比例函数的图象是双曲线.
(3)反比例函数的性质
①当k>0时,图象的两个分支分别在第一、三象限内,在各自的象限内,y随x的增大而减小.
②当k<0时,图象的两个分支分别在第二、四象限内,在各自的象限内,y随x的增大而增大.
③反比例函数图象关于直线y=±x对称,关于原点对称.
(4)k的两种求法
①若点(x0,y0)在双曲线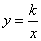 上,则k=x0y0.
上,则k=x0y0.
②k的几何意义:
若双曲线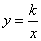 上任一点A(x,y),AB⊥x轴于B,则S△AOB
上任一点A(x,y),AB⊥x轴于B,则S△AOB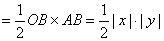

(5)正比例函数和反比例函数的交点问题
若正比例函数y=k1x(k1≠0),反比例函数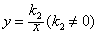 ,则
,则
当k1k2<0时,两函数图象无交点;
当k1k2>0时,两函数图象有两个交点,坐标分别为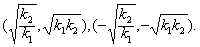 由此可知,正反比例函数的图象若有交点,两交点一定关于原点对称.
由此可知,正反比例函数的图象若有交点,两交点一定关于原点对称.

一元二次函数知识点汇总
1.定义:一般地,如果 是常数,
是常数, ,那么
,那么 叫做
叫做 的一元二次函数.
的一元二次函数.
2.二次函数 的性质
的性质
(1)抛物线
 的顶点是原点,对称轴是
的顶点是原点,对称轴是 轴.
轴.
(2)函数 的图像与
的图像与 的符号关系:
的符号关系:
①当 时
时 抛物线开口向上
抛物线开口向上 顶点为其最低点;②当
顶点为其最低点;②当 时
时 抛物线开口向下
抛物线开口向下 顶点为其最高点
顶点为其最高点
3.二次函数  的图像是对称轴平行于(包括重合)
的图像是对称轴平行于(包括重合) 轴的抛物线.
轴的抛物线.
4.二次函数 用配方法可化成:
用配方法可化成: 的形式,其中
的形式,其中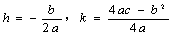 .
.
5.抛物线 的三要素:开口方向、对称轴、顶点.
的三要素:开口方向、对称轴、顶点.
① 决定抛物线的开口方向:
决定抛物线的开口方向:
当 时,开口向上;当
时,开口向上;当 时,开口向下;
时,开口向下; 越小,抛物线的开口越大,
越小,抛物线的开口越大, 越大,抛物线的开口越小。
越大,抛物线的开口越小。
②对称轴为平行于 轴(或重合)的直线,记作
轴(或重合)的直线,记作 .特别地,
.特别地, 轴记作直线
轴记作直线 .
.
③定点是抛物线的最值点[最大值( 时)或最小值(
时)或最小值( 时)],坐标为(
时)],坐标为( ,
, )。
)。
6.求抛物线的顶点、对称轴的方法
(1)公式法: ,∴顶点是
,∴顶点是 ,对称轴是直线
,对称轴是直线 .
.
(2)配方法:运用配方法将抛物线的解析式化为 的形式,得到顶点为(
的形式,得到顶点为( ,
, ),对称轴是
),对称轴是 .
.
(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以抛物线上纵坐标相等的两个点连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.
★用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失★
7.抛物线 中,
中, 的作用
的作用
(1) 决定开口方向及开口大小,这与
决定开口方向及开口大小,这与 中的
中的 完全一样.
完全一样.
(2) 和
和 共同决定抛物线对称轴的位置.由于抛物线
共同决定抛物线对称轴的位置.由于抛物线 的对称轴是直线
的对称轴是直线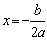 ,故:
,故:
① 时,对称轴为
时,对称轴为 轴;②
轴;② 时,对称轴在
时,对称轴在 轴左侧;③
轴左侧;③ 时,对称轴在
时,对称轴在 轴右侧.
轴右侧.
(3) 的大小决定抛物线
的大小决定抛物线 与
与 轴交点的位置.
轴交点的位置.
当 时,
时, ,∴抛物线
,∴抛物线 与
与 轴有且只有一个交点(0,
轴有且只有一个交点(0, ):
):
①  ,抛物线经过原点; ②
,抛物线经过原点; ② ,与
,与 轴交于正半轴;③
轴交于正半轴;③ ,与
,与 轴交于负半轴.
轴交于负半轴.
以上三点中,当结论和条件互换时仍成立.如抛物线的对称轴在 轴右侧,则
轴右侧,则  .
.
8. 二次函数由特殊到一般,可分为以下几种形式:
① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.
图像特征如下:

9.用待定系数法求二次函数的解析式
(1)一般式: .已知图像上三点或三对
.已知图像上三点或三对 、
、 的值,通常选择一般式.
的值,通常选择一般式.
(2)顶点式: .已知图像的顶点或对称轴,通常选择顶点式.
.已知图像的顶点或对称轴,通常选择顶点式.
(3)交点式:已知图像与 轴的交点坐标
轴的交点坐标 、
、 ,通常选用交点式:
,通常选用交点式: .
.
10.直线与抛物线的交点(或称二次函数与一次函数关系)
(1) 轴与抛物线
轴与抛物线 得交点为(
得交点为( )
)
(2)与 轴平行的直线
轴平行的直线 与抛物线
与抛物线 有且只有一个交点(
有且只有一个交点( ,
, ).
).
(3)抛物线与 轴的交点
轴的交点
二次函数 的图像与
的图像与 轴的两个交点的横坐标
轴的两个交点的横坐标 、
、 ,是对应一元二次方程
,是对应一元二次方程
 的两个实数根.抛物线与
的两个实数根.抛物线与 轴的交点情况可以由对应的一元二次方程的根的判别式判定:
轴的交点情况可以由对应的一元二次方程的根的判别式判定:
①有两个交点
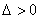
 抛物线与
抛物线与 轴相交;
轴相交;
②有一个交点(顶点在 轴上)
轴上)

 抛物线与
抛物线与 轴相切;
轴相切;
③没有交点

 抛物线与
抛物线与 轴相离.
轴相离.
(4)平行于 轴的直线与抛物线的交点
轴的直线与抛物线的交点
同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为 ,则横坐标是
,则横坐标是 的两个实数根.而根的存在情况仍如(3)一样由根的判别式判定。
的两个实数根.而根的存在情况仍如(3)一样由根的判别式判定。
(5)一次函数 的图像
的图像 与二次函数
与二次函数 的图像
的图像 的交点,由方程组
的交点,由方程组
 的解的数目来确定:
的解的数目来确定:
①方程组有两组不同的解时
 与
与 有两个交点;
有两个交点;
②方程组只有一组解时
 与
与 只有一个交点;③方程组无解时
只有一个交点;③方程组无解时
 与
与 没有交点.
没有交点.
(6)抛物线与 轴两交点之间的距离:若抛物线
轴两交点之间的距离:若抛物线 与
与 轴两交点为
轴两交点为 ,由于
,由于 、
、 是方程
是方程 的两个根,故由韦达定理知:
的两个根,故由韦达定理知:
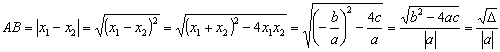
11.二次函数与一元二次方程的关系:
(1)一元二次方程 就是二次函数
就是二次函数 当函数y的值为0时的情况.
当函数y的值为0时的情况.
(2)二次函数 的图象与
的图象与 轴的交点有三种情况:有两个交点、有一个交点、没有交点;当二次函数
轴的交点有三种情况:有两个交点、有一个交点、没有交点;当二次函数 的图象与
的图象与 轴有交点时,交点的横坐标就是当
轴有交点时,交点的横坐标就是当 时自变量
时自变量 的值,即一元二次方程
的值,即一元二次方程 的根.
的根.
(3)当二次函数 的图象与
的图象与 轴有两个交点时,则一元二次方程
轴有两个交点时,则一元二次方程 有两个不相等的实数根;当二次函数
有两个不相等的实数根;当二次函数 的图象与
的图象与 轴有一个交点时,则一元二次方程
轴有一个交点时,则一元二次方程 有两个相等的实数根;当二次函数
有两个相等的实数根;当二次函数 的图象与
的图象与 轴没有交点时,则一元二次方程
轴没有交点时,则一元二次方程 没有实数根
没有实数根
12.二次函数的基本形式

1)二次函数基本形式: 的性质: a 的绝对值越大,抛物线的开口越小。
的性质: a 的绝对值越大,抛物线的开口越小。
(2) 的性质:上加下减。
的性质:上加下减。

(3) 的性质:结论:左加右减。
的性质:结论:左加右减。

(4) 的性质:
的性质:

4.二次函数由特殊到一般,可分为以下几种形式:
① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤
.

5.二次函数图像与性质:
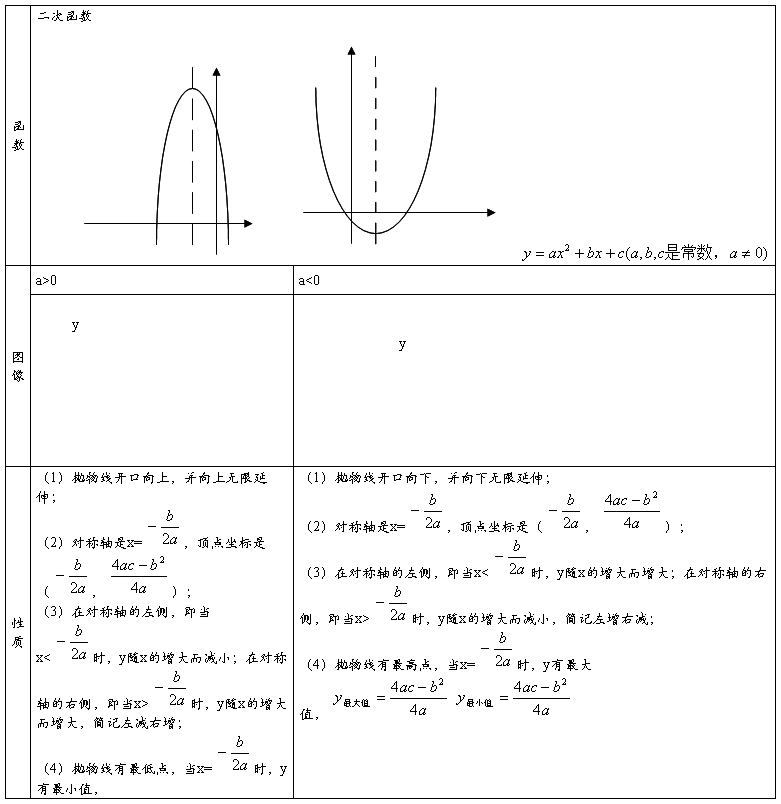
第二篇:二次函数知识点汇总(简而全)
★二次函数知识点汇总★
初三备课组 2012.2.13
1.定义:一般地,如果 是常数,
是常数, ,那么
,那么 叫做
叫做 的二次函数.
的二次函数.
2.二次函数 的性质
的性质
(1)抛物线
 的顶点是____,对称轴是____.(2)函数
的顶点是____,对称轴是____.(2)函数 的图像与
的图像与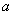 的符号关系.
的符号关系.
①当 时
时 抛物线开口向上
抛物线开口向上 顶点为其最低点;②当
顶点为其最低点;②当 时
时 抛物线开口向下
抛物线开口向下 顶点为其最高点
顶点为其最高点
3.二次函数  的图像是对称轴平行于(包括重合)
的图像是对称轴平行于(包括重合) 轴的抛物线.
轴的抛物线.
4.二次函数 用配方法可化成:
用配方法可化成: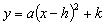 的形式,其中
的形式,其中 .
.
5.二次函数由特殊到一般,可分为以下几种形式:
① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.
6.抛物线的三要素:开口方向、对称轴、顶点.
①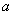 决定抛物线的开口方向:
决定抛物线的开口方向:
当 时,开口向上;当
时,开口向上;当 时,开口向下;
时,开口向下; 相等,抛物线的开口大小、形状相同.
相等,抛物线的开口大小、形状相同.
②平行于 轴(或重合)的直线____.特别地,
轴(或重合)的直线____.特别地, 轴记作直线
轴记作直线 .
.
7.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数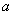 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.
相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.
8.求抛物线的顶点、对称轴的方法
(1)公式法: ,∴顶点是____,对称轴是直线____.
,∴顶点是____,对称轴是直线____.
(2)配方法:运用配方法将抛物线的解析式化为的____形式,得到顶点为( ),对称轴是____.
(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.
★用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失★
9.抛物线 中,
中, 的作用
的作用
(1)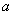 决定开口方向及开口大小,这与
决定开口方向及开口大小,这与 中的
中的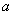 完全一样.
完全一样.
(2)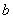 和
和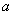 共同决定抛物线对称轴的位置.由于抛物线
共同决定抛物线对称轴的位置.由于抛物线 的对称轴是直线
的对称轴是直线 ,故:①____时,对称轴为
,故:①____时,对称轴为 轴;②
轴;② (即
(即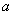 、
、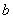 同号)时,对称轴在
同号)时,对称轴在 轴____侧;③
轴____侧;③ (即
(即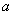 、
、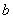 异号)时,对称轴在
异号)时,对称轴在 轴____侧.
轴____侧.
(3) 的大小决定抛物线
的大小决定抛物线 与
与 轴交点的位置.当
轴交点的位置.当 时,
时,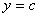 ,∴抛物线
,∴抛物线 与
与 轴有且只有一个交点( ):①
轴有且只有一个交点( ):①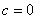 ,抛物线经过____; ②
,抛物线经过____; ②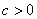 ,与
,与 轴交于正半轴;③
轴交于正半轴;③ ,与
,与 轴交于负半轴.以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在
轴交于负半轴.以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在 轴右侧,则
轴右侧,则  .
.
10.几种特殊的二次函数的图像特征如下:
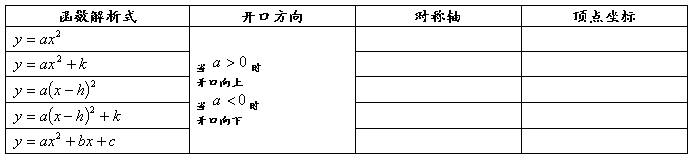
11.用待定系数法求二次函数的解析式
(1)一般式: .已知图像上三点或三对
.已知图像上三点或三对 、
、 的值,通常选择一般式.
的值,通常选择一般式.
(2)顶点式: .已知图像的顶点或对称轴,通常选择顶点式.
.已知图像的顶点或对称轴,通常选择顶点式.
(3)交点式:已知图像与 轴的交点坐标
轴的交点坐标 、
、 ,通常选用交点式:
,通常选用交点式: .
.
12.直线与抛物线的交点
(1) 轴与抛物线
轴与抛物线 得交点为( )
得交点为( )
(2)与 轴平行的直线
轴平行的直线 与抛物线
与抛物线 有且只有一个交点(
有且只有一个交点( ,
, ).
).
(3)抛物线与 轴的交点
轴的交点
二次函数 的图像与
的图像与 轴的两个交点的横坐标
轴的两个交点的横坐标 、
、 ,是对应一元二次方程
,是对应一元二次方程
 的两个实数根.抛物线与
的两个实数根.抛物线与 轴的交点情况可以由对应的一元二次方程的根的判别式判定:
轴的交点情况可以由对应的一元二次方程的根的判别式判定:
①有两个交点

 抛物线与
抛物线与 轴相交;
轴相交;
②有一个交点(顶点在 轴上)
轴上)

 抛物线与
抛物线与 轴相切;
轴相切;
③没有交点

 抛物线与
抛物线与 轴相离.
轴相离.
(4)平行于 轴的直线与抛物线的交点
轴的直线与抛物线的交点
同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为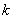 ,则横坐标是
,则横坐标是 的两个实数根.
的两个实数根.
(5)一次函数 的图像
的图像 与二次函数
与二次函数 的图像
的图像 的交点,由方程组
的交点,由方程组
 的解的数目来确定:
的解的数目来确定:
①方程组有两组不同的解时
 与
与 有两个交点;
有两个交点;
②方程组只有一组解时
 与
与 只有一个交点;③方程组无解时
只有一个交点;③方程组无解时
 与
与 没有交点.
没有交点.
(6)抛物线与 轴两交点之间的距离:若抛物线
轴两交点之间的距离:若抛物线 与
与 轴两交点为
轴两交点为 ,由于
,由于 、
、 是方程
是方程 的两个根,故
的两个根,故 

13.二次函数与一元二次方程的关系:
(1)一元二次方程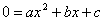 就是二次函数
就是二次函数 当函数y的值为0时的情况.
当函数y的值为0时的情况.
(2)二次函数 的图象与
的图象与 轴的交点有三种情况:有两个交点、有一个交点、没有交点;当二次函数
轴的交点有三种情况:有两个交点、有一个交点、没有交点;当二次函数 的图象与
的图象与 轴有交点时,交点的横坐标就是当
轴有交点时,交点的横坐标就是当 时自变量
时自变量 的值,即一元二次方程
的值,即一元二次方程 的根.
的根.
(3)当二次函数 的图象与
的图象与 轴有两个交点时,则一元二次方程
轴有两个交点时,则一元二次方程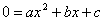 有两个不相等的实数根;当二次函数
有两个不相等的实数根;当二次函数 的图象与
的图象与 轴有一个交点时,则一元二次方程
轴有一个交点时,则一元二次方程 有两个相等的实数根;当二次函数
有两个相等的实数根;当二次函数 的图象与
的图象与 轴没有交点时,则一元二次方程
轴没有交点时,则一元二次方程 没有实数根
没有实数根
14.二次函数的应用:
(1)二次函数常用来解决最优化问题,这类问题实际上就是求函数的最大(小)值;
(2)二次函数的应用包括以下方面:分析和表示不同背景下实际问题中变量之间的二次函数关系;
运用二次函数的知识解决实际问题中的最大(小)值.
15.解决实际问题时的基本思路:(1)理解问题;(2)分析问题中的变量和常量;(3)用函数表达式表示出它们之间的关系;(4)利用二次函数的有关性质进行求解;(5)检验结果的合理性,对问题加以拓展等.
-
反比例函数知识点归纳 最经典最好的笔记
反比例函数知识点归纳一反比例函数的概念1可以写成的形式注意自变量x的指数为这一限制条件在解决有关自变量指数问题时应特别注意系数2也…
-
反比例函数中考知识点总结
反比例函数一基础知识1定义一般地形如y写成ykx1kkk为常数ko的函数称为反比例函数y还可以xxxykk为常数ko2反比例函数的…
-
反比例函数知识点归纳(重点)
中考复习反比例函数基础知识一反比例函数的概念1可以写成的形式注意自变量x的指数为这一限制条件在解决有关自变量指数问题时应特别注意系…
-
反比例函数知识点总结
反比例函数知识点总结知识点1反比例函数的定义一般地,形如y?个方面来理解:⑴x是自变量,y是x的反比例函数;⑵自变量x的取值范围是…
-
反比例函数知识点总结
反比例函数【基础知识】一、反比例函数的概念1.()可以写成()的形式,注意自变量x的指数为这一限制条件;,在解决有关自变量指数问题…
-
初中数学一次函数知识点总结
一次函数一次函数:一次函数图像与性质是中考必考的内容之一。中考试题中分值约为10分左右题型多样,形式灵活,综合应用性强。甚至有存在…
-
初中数学一次函数知识点总结(王晨晨)
初中数学一次函数知识点总结:一次函数与正比例函数的概念一般的,形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数。特别的…
-
初中数学一次函数知识点总结
一次函数知识点总结:一次函数:一次函数图像与性质是中考必考的内容之一。中考试题中分值约为10分左右题型多样,形式灵活,综合应用性强…
-
初二数学一次函数_一次函数知识点总结_初二数学一次函数复习
一次函数知识点总结基本概念:1、变量:在一个变化过程中可以取不同数值的量。常量:在一个变化过程中只能取同一数值的量。2、函数:一般…
-
初二数学一次函数知识点总结
一次函数知识点总结基本概念1、变量:在一个变化过程中可以取不同数值的量。常量:在一个变化过程中只能取同一数值的量。例题:在匀速运动…
-
八年级数学一次函数知识点总结
一次函数知识点总结一、函数1.变量的定义:在某一变化过程中,我们称数值发生变化的量为变量。变量还分为自变量和因变量。2.常量的定义…