等差数列的性质总结
二、等差数列
1.等差数列的定义: (d为常数)(
(d为常数)( );
);
2.等差数列通项公式:
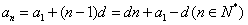 , 首项:
, 首项: ,公差:d,末项:
,公差:d,末项:
推广:  . 从而
. 从而 ;
;
3.等差中项
(1)如果 ,
, ,
, 成等差数列,那么
成等差数列,那么 叫做
叫做 与
与 的等差中项.即:
的等差中项.即: 或
或
(2)等差中项:数列 是等差数列
是等差数列

4.等差数列的前n项和公式:

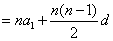


(其中A、B是常数,所以当d≠0时,Sn是关于n的二次式且常数项为0)
特别地,当项数为奇数 时,
时, 是项数为2n+1的等差数列的中间项
是项数为2n+1的等差数列的中间项
 (项数为奇数的等差数列的各项和等于项数乘以中间项)
(项数为奇数的等差数列的各项和等于项数乘以中间项)
5.等差数列的判定方法
(1)定义法:若 或
或 (常数
(常数 )
)
 是等差数列.
是等差数列.
(2) 等差中项:数列 是等差数列
是等差数列
 .
.
(3)数列 是等差数列
是等差数列
 (其中
(其中 是常数)。
是常数)。
(4)数列 是等差数列
是等差数列
 ,(其中A、B是常数)。
,(其中A、B是常数)。
6.等差数列的证明方法
定义法:若 或
或 (常数
(常数 )
)
 是等差数列.
是等差数列.
7.提醒:
(1)等差数列的通项公式及前 和公式中,涉及到5个元素:
和公式中,涉及到5个元素: 、
、 、
、 、
、 及
及 ,其中
,其中 、
、 称作为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。
称作为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。
(2)设项技巧:
①一般可设通项
②奇数个数成等差,可设为…, …(公差为
…(公差为 );
);
③偶数个数成等差,可设为…, ,…(注意;公差为2
,…(注意;公差为2 )
)
8..等差数列的性质:
(1)当公差 时,
时,
等差数列的通项公式 是关于
是关于 的一次函数,且斜率为公差
的一次函数,且斜率为公差 ;
;
前 和
和 是关于
是关于 的二次函数且常数项为0.
的二次函数且常数项为0.
(2)若公差 ,则为递增等差数列,若公差
,则为递增等差数列,若公差 ,则为递减等差数列,若公差
,则为递减等差数列,若公差 ,则为常数列。
,则为常数列。
(3)当 时,则有
时,则有 ,特别地,当
,特别地,当 时,则有
时,则有 .
.
注: ,
,
(4)若 、
、 为等差数列,则
为等差数列,则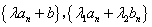 都为等差数列
都为等差数列
(5) 若{ }是等差数列,则
}是等差数列,则 ,…也成等差数列
,…也成等差数列
(6)数列 为等差数列,每隔k(k
为等差数列,每隔k(k
 )项取出一项(
)项取出一项( )仍为等差数列
)仍为等差数列
(7)设数列 是等差数列,d为公差,
是等差数列,d为公差, 是奇数项的和,
是奇数项的和, 是偶数项的和,
是偶数项的和, 是前n项的和
是前n项的和
1.当项数为偶数 时,
时,




2、当项数为奇数 时,则
时,则

(其中 是项数为2n+1的等差数列的中间项).
是项数为2n+1的等差数列的中间项).
(8)、 的前
的前 和分别为
和分别为 、
、 ,且
,且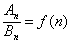 ,
,
则 .
.
(9)等差数列 的前n项和
的前n项和 ,前m项和
,前m项和 ,则前m+n项和
,则前m+n项和
(10)求 的最值
的最值
法一:因等差数列前 项是关于
项是关于 的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性
的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性 。
。
法二:(1)“首正”的递减等差数列中,前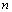 项和的最大值是所有非负项之和
项和的最大值是所有非负项之和
即当 由
由 可得
可得 达到最大值时的
达到最大值时的 值.
值.
(2) “首负”的递增等差数列中,前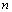 项和的最小值是所有非正项之和。
项和的最小值是所有非正项之和。
即 当 由
由 可得
可得 达到最小值时的
达到最小值时的 值.
值.
或求 中正负分界项
中正负分界项
法三:直接利用二次函数的对称性:由于等差数列前n项和的图像是过原点的二次函数,故n取离二次函数对称轴最近的整数时, 取最大值(或最小值)。若S p = S q则其对称轴为
取最大值(或最小值)。若S p = S q则其对称轴为
注意:解决等差数列问题时,通常考虑两类方法:
①基本量法:即运用条件转化为关于 和
和 的方程;
的方程;
②巧妙运用等差数列的性质,一般地运用性质可以化繁为简,减少运算量.
第二篇:等差数列的性质总结
等差数列的性质总结
1. 等差数列的定义: (
( 为常数)(
为常数)( );
);
2.等差数列通项公式:
 ; 首项:
; 首项: ;公差:
;公差:  ;末项:
;末项: .
.
推广: . 从而
. 从而 ;
;
3.等差中项
(1)如果 ,
, ,
, 成等差数列,那么
成等差数列,那么 叫做
叫做 与
与 的等差中项.即:
的等差中项.即: 或
或
(2)等差中项:数列 是等差数列
是等差数列

4.等差数列的前n项和公式:




(其中 是常数,所以当
是常数,所以当 时,
时, 是关于
是关于 的二次式且常数项为0)
的二次式且常数项为0)
特别地,当项数为奇数 时,
时, 是项数为
是项数为 的等差数列的中间项
的等差数列的中间项
 (项数为奇数的等差数列的各项和等于项数乘以中间项)
(项数为奇数的等差数列的各项和等于项数乘以中间项)
5. 等差数列的判定方法
(1)定义法:若 或
或 (常数
(常数 )
)
 是等差数列.
是等差数列.
(2)中项公式法:数列 是等差数列
是等差数列
 .
.
(3)通项公式法:数列 是等差数列
是等差数列
 (其中
(其中 是常数)。
是常数)。
(4)前 项和公式法:数列
项和公式法:数列 是等差数列
是等差数列
 ,(其中
,(其中 是常数)。
是常数)。
6. 等差数列的证明方法
定义法:若 或
或 (常数
(常数 )
)
 是等差数列.
是等差数列.
7. 考点提醒:
(1)等差数列的通项公式及前 和公式中,涉及到5个元素:
和公式中,涉及到5个元素: 、
、 、
、 、
、 及
及 ,其中
,其中 、
、 称作为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。
称作为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。
(2)设项技巧:
①一般可设通项
②奇数个数成等差,可设为…, …(公差为
…(公差为 );
);
③偶数个数成等差,可设为…, ,…(注意;公差为
,…(注意;公差为 )
)
8. 等差数列的性质:
(1)当公差 时,
时,
等差数列的通项公式 是关于
是关于 的一次函数,且斜率为公差
的一次函数,且斜率为公差 ;
;
前 和
和 是关于
是关于 的二次函数且常数项为0.
的二次函数且常数项为0.
(2)若公差 ,则为递增等差数列,若公差
,则为递增等差数列,若公差 ,则为递减等差数列,若公差
,则为递减等差数列,若公差 ,则为常数列。
,则为常数列。
(3)当 时,则有
时,则有 ,特别地,当
,特别地,当 时,则有
时,则有 .
.
注: ,
,
(4)若 、
、 为等差数列,则
为等差数列,则 都为等差数列
都为等差数列
(5)若{ }是等差数列,则
}是等差数列,则 ,…也成等差数列
,…也成等差数列
(6)数列 为等差数列,每隔
为等差数列,每隔 项取出一项(
项取出一项( )仍为等差数列
)仍为等差数列
(7)设数列 是等差数列,
是等差数列, 为公差,
为公差,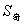 是奇数项的和,
是奇数项的和, 是偶数项项的和,
是偶数项项的和, 是前n项的和
是前n项的和
1.当项数为偶数 时,
时,




2、当项数为奇数 时,则
时,则
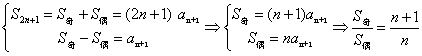
(其中 是项数为
是项数为 的等差数列的中间项).
的等差数列的中间项).
(8) 、
、 的前
的前 和分别为
和分别为 、
、 ,且
,且 ,
,
则 .
.
(9)等差数列 的前n项和
的前n项和 ,前
,前 项和
项和 ,
, 则前
则前 项和
项和 ;
;
若 ,
, ,则
,则 ;
;
若
 ,则
,则 .
.
(10) 求 的最值
的最值
法一:因等差数列前 项和是关于
项和是关于 的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性
的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性 。
。
法二:
(1)“首正”的递减等差数列中,前 项和的最大值是所有非负项之和
项和的最大值是所有非负项之和
即当 由
由 可得
可得 达到最大值时的
达到最大值时的 值.
值.
(2) “首负”的递增等差数列中,前 项和的最小值是所有非正项之和。
项和的最小值是所有非正项之和。
即 当 由
由 可得
可得 达到最小值时的
达到最小值时的 值.
值.
或求 中正负分界项
中正负分界项
法三:直接利用二次函数的对称性:由于等差数列前n项和的图像是过原点的二次函数,故n取离二次函数对称轴最近的整数时, 取最大值(或最小值)。若
取最大值(或最小值)。若 ,则其对称轴为
,则其对称轴为
注意:解决等差数列问题时,通常考虑两类方法:
①基本量法:即运用条件转化为关于 和
和 的方程;
的方程;
②巧妙运用等差数列的性质,一般地运用性质可以化繁为简,减少运算量.
-
等比数列的性质总结
等比数列性质1等比数列的定义2通项公式ana1qn1anan1qq0n2且nNq称为公比a1qqABnna1q0AB0首项a1公比…
-
高中数学等差数列性质总结大全
等差数列的性质总结1.等差数列的定义:an?an?1?d(d为常数)(n?2);2.等差数列通项公式:an?a1?(n?1)d?d…
-
等差数列的性质总结
1.等差数列的定义式:an?an?12.等差数列通项公式:an?a1?(n?1)d?dn?a1?d(n?N*),首项:a1,公差:…
-
等差等比数列的性质总结
等差等比数列的性质一等差数列1等差数列的定义anan1dd为常数n22等差数列通项公式ana1n1ddna1dnN首项a1公差d末…
-
数列知识点所有性质总结
一、等差数列1.等差数列的定义:(d为常数)();2.等差数列通项公式:,首项:,公差:d,末项:推广:.从而;3.等差中项(1)…
-
等差数列知识点总结
等差数列1.定义一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数…
-
等差数列知识点题型总结
等差数列一、知识回顾题型一:等差数列的基本运算1、等差数列{an}前9项的和等于前4项的和.若a1=1,ak+a4=0,则2.已知…
-
等差数列题型总结、知识点
等差数列一.等差数列知识点:1:①如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常…
-
数列公式性质总结
一定义(n≥2,n∈N)1等差:an-an?1=d1′等比:二通项公式1?an=q(q≠0)an?1an?a1?(n?1)d(推导…
-
等差数列的性质总结
1.等差数列的定义式:an?an?12.等差数列通项公式:an?a1?(n?1)d?dn?a1?d(n?N*),首项:a1,公差:…
-
等差数列知识点总结
等差数列知识清单1、等差数列定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,…