数学实验报告

         学生姓名：      陆莹       

         学    号：    20121315021  

         院    部：  数学与统计学院  

         专    业：   统计学         

         班    级：    （1）班      

         任课教师：    费文龙        

实验报告1

实验课程 大学数学实验    实验名称  Mathematica入门    实验日期 20##-9-11     指导老师 费文龙

专业  统计学      年级  2012       姓名  陆莹       学号  20121315021             得分        

实验目的：

熟悉Mathematica软件包的使用。

实验内容：

1、用两种方式编写如下自定义函数，并求其导数f’(x)在x=-2.0,x=1.0,x=5.0处的值

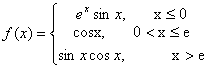
2、分别用Plot3D, ParametricPlot3D函数画出（）的图像。

3、用Mathematica实现一个四人追逐问题，给出结果并划出追逐路线（如下图）。

实验要求：

1、撰写实验报告；

2、写出试验过程中所使用的Mathematica程序或语句和计算结果；

实验步骤：

1.Int[1]:=f[x_]:=E^x Sin[x]/;x£0;

          f[x_]:=Cos[x]/;0<x£E;

          f[x_]:=Sin[x]*Cos[x]/;x>E;

          g[x_]=D[f[x],x];

          N[{g[-2.0],g[1.0],g[5.0]}]

2.Int[2]:=Plot3D[1-x^2-y^2,{x,0,1},{y,0,1}]

  Int[3]:=x[s_,t_]:=Sin[s] Cos[t];

          y[s_,t_]:=Sin[s] Sin[t];

          z[s_,t_]:=Cos[s];

          ParametricPlot3D[{x[s,t],y[s,t],z[s,t]},{s,0,Pi},{t,0,Pi/2}]

3.

Int[4]:=

v=1;t=18;dt=0.02;n=t/dt;

T={{{0,10}},{{10,10}},{{10,0}},{{0,0}}};

d=Sqrt[(x2-x1)^2+(y2-y1)^2];

For[j=1,j£n,j++,

  For[i=1,i£4,i++,x1=T[[i,j,1]];y1=T[[i,j,2]]

     If[i¹4,x2=T[[i+1,j,1]];

          y2=T[[i+1,j,2]], x2=T[[1,j,1]];y2=T[[1,j,2

         ]

        ]

      ];

   x1=x1+v*dt*(x2-x1)/d;y1=y1+v*dt*(y2-y1)/d;

   T[[i]]=Append[T[[i]],{x1,y1}]]];

P=Graphics[{Line[T[[1]]],Line[T[[2]]],Line[T[[3]]],Line[T[[4]]],Line[{{0,10},{10,10},{10,0},{0,0},{0,10}}]}];

Show[P,AspectRatio®1]

实验结果：

1.Out[1]={-0.179379,-0.841471,-0.839072}

2.Out[2]=

Out[3]=

Out[4]=

  

实验报告2

实验课程 大学数学实验    实验名称  pi的近似求解      实验日期 20##-10-16     指导老师 费文龙

专业  统计学      年级  2012       姓名  陆莹       学号  20121315021             得分        

实验目的：

练习的求解方法。

实验内容：

1、用反正切函数的幂级数展开式结合有关公式求，若要精确到以40位、50位数字，试比较简单公式和Machin公式所用的项数。

2、用数值积分计算，分别给出用梯形法和Simpson法精确到10位数字、用Simpson法精确到15位数字时所用的项数n及的近似值

3、用计算机模拟Buffon实验，给出n=1,000、10,000、1,000,000时的模拟结果。

实验要求：

撰写实验报告

写出试验过程中所使用的Mathematica程序或语句和计算结果

实验步骤：

1、

m=N[Pi,40]

n=N[Pi,50]

T[n_,x_]:=Sum[(-1)^(k-1)*x^(2 k-1)/(2 k-1),{k,1,n}];

N[4*T[20000,1],40]

3.141592653589793238462643383279502884197

3.1415926535897932384626433832795028841971693993751

3.141542653589824488462545727030247513093

Print[N[16*T[30,1/5]-4*T[30,1/239],50]]

3.1415926535897932384626433832795028841971693411490

当n=20000时，简单公式结果为：

3.141542653589824488462545727030247513093

只精确到第四位。

当n=30时，Machin公式结果为：

3.1415926535897932384626433832795028841971693411490

精确到44位。

2、当n=30000时，用简单公式可精确到第9位。

i=10;s=N[Pi, 20]

f[x_]:=4/(1+x^2);

s1[n_]:=(Sum[f[k/n],{k,1,n-1}]+(f[0]+f[1])/2)/n;

s2[n_]:=(f[0]+f[1]+2*Sum[f[k/n],{k,1,n-1}] +

        4*Sum[f[(k-1/2)/n],{k,1,n}])/(6*n); While[

  Abs[N[s2[i],20]-s]>10^(-10),i++];

Print[i]

N[s2[i],17]

3.1415926535897932385

14

3.1415926535074467

即当n=14时，用Simpson法可精确到第10位，Pi的近似值为3.1415926535

While[Abs[N[s2[i],20]-s]>10^(-15),i++];

Print[i]

N[s2[i],20]

93

3.1415926535897922801

即当n=93时，Simpson法可精确到第15位，Pi的近似值为3.14159265358979

3、

a=20;l=10;

s3[n_]:=

  Block[{i,m=0},

    For[i=n,i>0,i--,

      m=m+If[Random[]*a/2<=l/2*Sin[Random[]*Pi/2],1,0]];

    N[2*l*n/(a*m),20]];

s3[1000]

s3[10000]

s3[1000000]

3.0674846625766871166

3.1201248049921996880

3.1449310002138553080

实验报告3

实验课程 大学数学实验    实验名称       房贷         实验日期 20##-10-30     指导老师 费文龙

专业  统计学      年级  2012       姓名  陆莹       学号  20121315021             得分        

实验目的：

熟悉差分方程的求解以及相关金融问题的数学建模方法。

实验内容：

1、假设住房贷款的年利率表为

试根据以上年率表，计算出每万元1~10年的月还款表。

2、小李夫妇曾经准备申请商业贷款10万元用于购置住房，每月还款880.66元，25年还清。
房产商介绍的一家金融机构提出：贷款10万元，每半月还款440.33元, 22年还清, 不过由于中介费手续费等原因，贷款时要预付4000元。
小李考虑，虽然预付费用不少，可是减少三年还款期意味着减少还款近3万2千元，而每月多跑一趟，那不算什么.这机构的条件似乎还是蛮优惠的。
试通过计算两种贷款的利率水平，比较哪种贷款更优惠。

3、 试比较两种提前还款方式的优劣（附加）
A、提前还款额冲抵最后月份的本金，每月的还款额度不变，还款时间缩短；
B、提前还款额冲抵本金后，将剩余的贷款重新计算月还款额减少，还款时间不变。

实验要求：

撰写实验报告

写出试验过程中所使用的Mathematica程序或语句和计算结果

实验步骤：

1.设：n（n=1,2,…，10）年期月还款金额为a[n]元,n年期第k（k=0,1,…12*n）个月剩余本金为b[k]元，年利率为r,则b[12*n]=0元,当n<=5时，r=0.0477,当n>5时，r=0.0504

每万元1~10年月还款如上。

2、商业贷款

实验结果

金融机构贷款

实验结果

即年利率为9.699%

前者较为优惠

实验报告4

实验课程 大学数学实验    实验名称   方程迭代求解     实验日期 20##-11-13     指导老师 费文龙

专业  统计学      年级  2012       姓名  陆莹       学号  20121315021             得分       

实验目的：

熟悉迭代法的基本概念，并用迭代法求解方程、方程组的根。

实验内容：

1、选用几种迭代格式求的近似值，并比较收敛速度。

2、对方程组，设A的对角元素，
令为对角阵，
将方程组改写成，或
用这种迭代格式求解方程组，其中
                 ，b=0
构造一种迭代格式，进行迭代，
比较上述两种迭代格式的迭代次数和迭代精度。

实验要求：

撰写实验报告

写出试验过程中所使用的Mathematica程序或语句和计算结果

实验步骤：

1、一般迭代格式

Iterate[f_,x0_,n_Integer] :=

  Module[{t={},i,temp=x0},AppendTo[t,temp];

    For[i=1,i<=n,i++,temp=f[temp];AppendTo[t,temp]];t]

f[x_]:=x/2+1/x^2;

Iterate[f,1.,17]

实验结果

{1., 1.5, 1.19444, 1.29814, 1.24248, 1.26901, 1.25547, 1.26217, 1.2588,

1.26048, 1.25964, 1.26006, 1.25985, 1.25996, 1.2599, 1.25993, 1.25992,

1.25992}

所以，采用一般迭代格式，近似值为1.25992，需迭代17次。

牛顿迭代

f[x_]:=x^3-2;g[x_]=Dt[f[x],x];

h[x_]:=x-f[x]/g[x];Iterate[h,1.,5]

实验结果

{1., 1.33333, 1.26389, 1.25993, 1.25992, 1.25992}

所以，采用牛顿迭代格式，近似值为1.25992，需迭代5次。

2、迭代格式

LSIterate[m_,f_List,f0_List,n_Integer] :=

  Module[{i,var=f0,t=Table[{},i,n}]},

    For[i=1,i<=n,i++,t[[i]]=var;var=m.var+f];t]

M = {{3,-1,1},{1,2,1},{1,1,-1}};f={0,0,0};f0={0,0,

    0};LSIterate[M,f,f0,10]

实验结果：

{{0, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 0, 0}}

Jacob迭代格式

JacobIterate[a_,b_List,x0_List,n_Integer]:=

  Module[{ad=Length[a],i,j,k,var=var1=x0},

    For[i=1,i<=ad,i++,

      If[a[[i,i]] == 0,Print["a[",i,",",i,"]=0."];Abort[]]];

    For[i=1,i<=n,i++,Print[var];

      For[j=1,j<=ad,j++,

        var[[j]]=

          N[(b[[j]]-Sum[a[[j,k]]*var[[k]],{k,ad}])/a[[j,j]]+var[[j]],

            20]]; var = var1;];]

a={{2, -1, 1}, {1, 1, 1}, {1, 1, -2}};b={0,0,0};x0={0, 0,

    0};JacobIterate[a,b,x0,10]

实验结果：

{0, 0, 0}

{0, 0, 0}

{0, 0, 0}

{0, 0, 0}

{0, 0, 0}

{0, 0, 0}

{0, 0, 0}

{0, 0, 0}

{0, 0, 0}

{0, 0, 0}

实验报告5

实验课程 大学数学实验    实验名称     分形混沌       实验日期 20##-11-27     指导老师 费文龙

专业  统计学      年级  2012       姓名  陆莹       学号  20121315021             得分       

实验目的：

了解有关分形和混沌的基本理论，能够用Mathematica软件绘制出一些简单的分形和混沌图形。

实验内容：

1、用Mathematica软件绘制一个分形的图形，图形类别自选

2、令，其中，绘制出相应的IFS吸引子图形，并取不同的s，观察图形的变化。

3、用Mathematica软件绘制一个混沌的图形，图形类别自选

4、谈谈你所认识的分形和混沌

实验要求：

撰写实验报告

写出试验过程中所使用的Mathematica程序或语句和计算结果

实验步骤：

1、Koch雪花曲线

redokoch[ptlist_List]:=

  Block[{tmp={},i,pnum=Length[ptlist]},

    For[i=1,i<pnum,i++,

      tmp=Join[

          tmp,{ptlist[[i]],

            ptlist[[i]]*2/3+

ptlist[[i+1]]/3,(ptlist[[i]]+ptlist[[i+1]])/

                2+{ptlist[[i]][[2]]-ptlist[[i+1]][[2]],

                  ptlist[[i+1]][[1]]-ptlist[[i]][[1]]}*Sqrt[3]/6,

            ptlist[[i]]/3+ptlist[[i+1]]*2/3,ptlist[[i+1]]}]];tmp]

lnko01={{0, 0}, {1, 0}};Show[

  Graphics[Line[Nest[redokoch,lnko01,5]],AspectRatio->Sqrt[3]/6]]

2、

s=0.5+0.5*I;p1=0.5;w1[z_]:=s*z+1;p2=0.5;w2[z_]:=s*z-1;

w[z_]:=Block[{tmp},tmp=Random[];

    Which[tmp<p1,w1[z],tmp<1,w2[z]]];

Array[mu,{150,150}];

showIFS[z0_,shrange_List,divi_List,nmax_]:=

  Block[{i,j,z=z0,a=divi[[1]],b=divi[[2]],temp1,temp2,mumax=0},

     For[i=a,i>=1,i--,For[j=b,j>=1,j--,mu[i,j]=0]];

    For[i=nmax,i>=1,i--,

      temp1=Floor[

            divi[[1]]*(Re[z]- shrange[[1]][[1]])/(shrange[[2]][[1]]-

                    shrange[[1]][[1]])]+1;

      temp2=Floor[

            divi[[2]]*(Im[z]-shrange[[1]][[2]])/(shrange[[2]][[2]]-

                    shrange[[1]][[2]])]+1;mu[temp1,temp2]++;z=

w[z];];

    For[i=a,i>=1,i--,

      For[j=b,j>=1,j--,mumax=Max[mumax,mu[i,j]]]];

    mu1=Table[GrayLevel[1-N[mu[j,i]]/mumax],{i,a},{j,b}];

    Show[Graphics[RasterArray[mu1]]]]

showIFS[0+I 0,{{-0.1,-0.1},{1.1,1.1}},{150,150},100000]

实验结果：

3、

Feigenbaum[n_Integer,x0_]:=

    Module[{A ={},a,i,temp,B={}},

      For[a=1,a<=n,a++,temp=x0;A={};

        For[i=1,i<=50,i++,temp=4*a*temp*(1-temp)/n];

        For[i=51,i<=100,i++,temp=4*a*temp*(1-temp)/n;

          AppendTo[A,{4*a/n,temp}]];

        AppendTo[B,

          ListPlot[A,PlotStyle->{PointSize[0.005]},

            DisplayFunction->Identity]]];

      Show[B,DisplayFunction->$DisplayFunction]];

Feigenbaum[1000,0.5]

4、分形：分形具有无限嵌套层次的精细结构，并且在不同尺度下保持相似属性。

混沌：对初值非常敏感，不是随机的。