数学实验报告

数学实验报告

实验1（定积分）

实验目的

1.加深对定积分概念的理解。

2.学会用MATLAB计算定积分。

实验内容

1.用数值计算和图形展示相结合的方法研究函数的积分和随分割细度的变化趋势。

2.用数值方法和符号演算计算定积分。

求由抛物线 y=2*x²与y=x²+3所围成的图形面积A。

解：

x=-3:0.1:3;

y1=2*x.^2;

y2=x.^2+3;

plot(x,y1,x,y2)

syms x

f=(x.^2+3)-2*x.^2;

A=int(f,x,-sqrt(3),sqrt(3))

结果为

A =

4*3^(1/2)

实验2（常微分方程）

实验目的

1.了解常微分方程的基本概念。

2.了解常微分方程的解析解。

3.了解常微分方程的数值解。

4.学习、掌握MATLAB软件有关的命令。

实验内容

常微分模型的建立及求解。

求解

解：

function z=dy1(x,y);

z=[y(2);2*y(2)-3*y(1)]

y0=[1;0];

[x,y]=ode23s('dy1',[0,30],y0);

plot(x,y(:,1),'r:',x,y(:,2),'k-');

xlabel('x')

ylabel('y')

结果为

y =

C1*exp(3*x)+C2*exp(-x)

y =

1/4*exp(3*x)+3/4*exp(-x)

实验3（线性规划）

实验目的

1.了解线性规划求解的基本方法。

2.学习、掌握用MATLAB求解线性规划的命令。

实验内容

线性规划的求解。

求解模型

解：

c=[6 3 4];

A=[0 1 0];

b=[50];

Aeq=[1 1 1];

beq=[120];

vlb=[30;0;20];

vub=[ ];

[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)

结果为

x =

30.0000

50.0000

40.0000

fval =

490.0000

实验4（非线性规划）

实验目的

1.了解非线性规划求解的基本方法。

2.学习、掌握用MATLAB求解非线性规划的命令。

实验内容

非线性规划的求解。

S.t.

解：

化为标准形

S.t.

H=[1 0;0 1];

c=[-1,-2];

A=[2 3 ;1 4];

b=[6;5];

aeq=[];

beq=[];

vlb=[0;0];

vub=[];

[x,fval]=quadprog(H,c,A,b,aeq,beq,vlb,vub)

结果为

x =

0.7647

1.0588

fval =

-2.0294

实验5（数据统计分析）

实验目的

1.加深对统计基本概念的理解。

2.参数估计。

3.假设检验。

4.学习、掌握用MATLAB进行参数估计和假设检验的命令。

实验内容

参数估计和假设。

随机抽查某专业60名同学“高等代数”课程的期末考试成绩，成绩如下：

93 75 83 93 91 85 84 82 77 76 77 95 94 89 91 88 86 83 96 81 79 97 78 75 67 69 68 84 83 81 75 66 85 70 94 84 83 82 80 78 74 73 76 70 86 76 90 89 71 66 86 73 80 94 79 78 77 63 53 55

试统计该专业学生“高等代数”课程成绩的分布规律。

解：

x=[|93 75 83 93 91 85 84 82 77 76 77 95 94 89 91 88 86 83 96 81 79 97 78 75 67 69 68 84 83 81 75 66 85 70 94 84 83 82 80 78 74 73 76 70 86 76 90 89 71 66 86 73 80 94 79 78 77 63 53 55]

T=[mean(x),median(x),var(x),std(x),kurtosis(x),skewness(x)]

T =

80.1000 80.5000 94.2949 9.7106 3.1529 -0.4682

该专业学生“高等代数”课程成绩的平均分为80.1分，中位数为80.5分，方差为94.2949，标准差为9.7106，峰度为3.1529，偏度系数为-0.4682。

>> hist(x,5)

>> normplot(x)

>> [muhat,sigmahat,muci,sigmaci]=normfit(x)

muhat =

80.1000

sigmahat =

9.7106

muci =

77.5915

82.6085

sigmaci =

表明该专业学生“高等代数”课程成绩的平均分为80.1分，方差为9.7106，均值的0.95置信区间为[77.5915， 82.6085]，方差的0.95的置信区间为[8.2310,11.8436]。

>> [h,sig,ci]=ttest(x,80.1)

h =

sig =

ci =

77.5915 82.6085

实验6(回归分析)

实验目的

1.回归分析的基本方法。

2.学习、掌握用MATLAB进行回归分析的命令。

实验内容

1.一元、多元线性回归。

2.一元、多元非线性回归。

试研究这些数据所包含的规律性

x=[1 1 4 6 8 11 14 17 21]
Y=[2.49 3.30 3.68 12.20 27.04 61.10 108.80 170.90 275.50]

解：

x=[1 1 4 6 8 11 14 17 21]' ;

Y=[2.49 3.30 3.68 12.20 27.04 61.10 108.80 170.90 275.50]';

plot(Y,X,'*')

>> X=[ones(10,0) x];

Warning: Concatenation involves an empty array with incorrect number of rows.

>> Y=[2.49 3.30 3.68 12.20 27.04 61.10 108.80 170.90 275.50]';

>> [b,bint,r,rint,stats]=regress(Y,X)

Warning: R-square and the F statistic are not well-defined unless X has a column of ones.

Type "help regress" for more information.

结果为

b =

9.6104

bint =

6.7852 12.4356

r =

-7.1204

-6.3104

-34.7616

-45.4625

-49.8433

-44.6145

-25.7458

7.5230

73.6813

rint =

-109.9759 95.7351

-109.2061 96.5853

-132.5522 63.0289

-138.8884 47.9635

-140.1529 40.4663

-134.1192 44.8901

-117.0446 65.5531

-81.6269 96.6729

23.8817 123.4810

stats =

1.0e+003 *

0.0005 NaN NaN 1.7486

回归方程为

Y=6.7852 +12.4356x

>> rcoplot(r,rint)

z=6.7852+12.4356*x

plot(x,Y,'k+',x,z,'r')

实验7（随机模拟）

实验目的

1.理解蒙特卡罗法的基本思想。

2.学会用随机模拟法解决一些常用的随机模拟计算。

3.学习、掌握用MATLAB进行计算机模拟命令。

实验内容

1随机数的生成。

蒙特卡罗法初步。

随机变量X表示随机到达的人数，分布如下：

模拟十分钟内到达的状况。

解：

>> n=20;n(j)=0;x=[];

for j=1:10;

x(j)=unifrnd(0,1);

if x(j)<0.3

n(j)=0;

elseif x(j)<0.8

n(j)=1;

else n(j)=2;

end;

end

结果为

>> x

x =

0.5113 0.7764 0.4893 0.1859 0.7006 0.9827 0.8066 0.7036 0.4850 0.1146

>> n

n =

1 1 1 0 1 2 2 1 1 0

实验8（非线性方程的迭代解法）

实验目的

1.了解迭代法的基本思想。

2.体验非线性方程迭代解法的发展历程。

实验内容

1.简单迭代与不动点。

2.牛顿迭代法、割线法。

用牛顿迭代法求解。

解：

牛顿迭代法的迭代函数为

>> x(1)=19;

for i=1:10

x(i+1)=x(i)-((x(i)^5-3*x(i)^3-2*x(i)^2+2)/(5*x(i)^4-9*x(i)^2-4*x(i)))

end

结果为

x =

19.0000 15.2134 0.4893 0.1859 0.7006 0.9827 0.8066 0.7036 0.4850 0.1146

实验9（函数图形显示）

实验目的

1.学会用MATLAB软件作平面函数在各种坐标系下的图形。

2.学会用MATLAB软件作空间函数在各种坐标系下的图形。

实验内容

1.平面函数在各种坐标系下的图形。

2.空间函数在各种坐标系下的图形。

锥面：，其参数方程为

x=3vsinu； y=2vcosu； z=v；

解：

u=[0:0.01:2*pi 0:0.01:2*pi];

v=0:0.01:2*pi;

[u,v]=meshgrid(u,v);

x=3.*v.*sin(u);

y=2.*v.*cos(u);

z=v;

mesh(x,y,z)

xlabel('x');

ylabel('y');

zlabel('z');

结果为

实验10（π的近似计算）

实验目的

1.了解圆周率π的计算历程。

2.体验π的计算方法的发展历程。

3.学习、掌握MATLAB软件的有关命令。

实验内容

使用不同方法π的近似值。

(1)用刘徽的迭代公式计算π的近似值。

解：

x=1;

for i=1:12

x=sqrt(2-sqrt(4-x^2));

S=(3*2^i*x);

End

>> vpa(S,9)

ans =

3.14159265

>> vpa(S,100)

ans =

3.141592645321215737652664756751619279384613037109375000000000000000000000000000000000000000000000000

>> vpa(S,30)

ans =

3.14159264532121573765266475675

(2)用韦达公式计算π的近似值。

解：

x=1;

D=zeros(10,3);

for i=1:10

x=x*cos(pi/2^(i+1));

pai=2/x;

error=abs(pi-pai);

D(i,:)=[i',pai',error'];

End

>> vpa(D,20)

ans =

[1., 2.8284271247461900976, .31316552884360326914]

[2., 3.0614674589207182542, .80125194669074861764e-1]

[3., 3.1214451522580519693, .20147501331741146657e-1]

[4., 3.1365484905459388720, .50441630438542439663e-2]

[5., 3.1403311569547525117, .12614966350406042750e-2]

[6., 3.1412772509327728798, .31540265702023617678e-3]

[7., 3.1415138011443008992, .78852445492216816092e-4]

[8., 3.1415729403670913378, .19713222701778221335e-4]

[9., 3.1415877252771591266, .49283126339894067769e-5]

[10., 3.1415914215111997443, .12320785933717104399e-5]

>> vpa(D,30)

ans =

[1., 2.82842712474619009760337744842, .313165528843603269137929601129]

[2., 3.06146745892071825423386144394, .801251946690748617641020246083e-1]

[3., 3.12144515225805196934061314096, .201475013317411466573503275868e-1]

[4., 3.13654849054593887203168378619, .504416304385424396627968235407e-2]

[5., 3.14033115695475251172297248559, .126149663504060427499098295812e-2]

[6., 3.14127725093277287982118650689, .315402657020236176776961656287e-3]

[7., 3.14151380114430089918187150033, .788524454922168160919682122767e-4]

[8., 3.14157294036709133777662827924, .197132227017782213351893005893e-4]

[9., 3.14158772527715912659118657757, .492831263398940677689097356051e-5]

[10., 3.14159142151119974428752357198, .123207859337171043989656027406e-5]

实验11（数值微分）

实验目的

1.了解求解数值微分的基本方法。

2.了解误差分析和步长优化。

3.会使用差分公式求解数值微分。

4.学习，掌握MATLAB软件的有关命令。

实验内容

1.中心差分公式。

2.前向微分和后向微分公式。

设

（1）分别用前差公式（17.8）和后差公式（17.13），步长分别为h=0.1,0.01,0.001和0.0001，计算的近似值，精度为小数点后9位，并与准确值对比。

解：

syms x;

y=cos(2*x^2-3);

dy2=diff(y,x,2)

dy2=-16*cos(2*x^2-3)*x^2-4*sin(2*x^2-3)

digits(9);

x0=0.7;

for k=1:4

h(k)=10^(-k);

x1=x0:h(k):x0+3*h(k);

x2=x0:-h(k):x0-3*h(k);

x3=x0+h(k):-h(k):x0-h(k);

y1=vpa(cos(2*x1.^2-3));

y2=vpa(cos(2*x2.^2-3));

y3=vpa(cos(2*x3.^2-3));

dy1(k)=(2*y1(1)-5*y1(2)+4*y1(3)-y1(4))/(h(k)^2);

dy2(k)=(2*y2(1)-5*y2(2)+4*y2(3)-y2(4))/(h(k)^2);

dy3(k)=(y3(1)-2*y3(2)+y3(3))/(h(k)^2);

dy=-16*cos(2*x0^2-3)*x0^2-4*sin(2*x0^2-3);

errdy1(k)=vpa(abs(dy1(k)-dy));

errdy2(k)=vpa(abs(dy2(k)-dy));

errdy3(k)=vpa(abs(dy3(k)-dy));

end

[h',dy1',errdy1',dy2',errdy2',dy3',errdy3']

结果为

ans =

[ 1/10, 9.30178260, 2.29410280, 7.84214560, .83446580, 6.86163310, .14604670]

[1/100, 7.02454000, .1686020e-1, 7.02292000, .1524020e-1, 7.00622000, .145980e-2]

[1/1000, 7.01300000, .532020e-2, 7.01200000, .432020e-2, 7.00800000, .32020e-3]

[1/10000, 6.50000000, .50767980, 6.70000000, .30767980, 7.00000000, .767980e-2]

x0=0.7;

dy=-16*cos(2*x0^2-3)*x0^2-4*sin(2*x0^2-3);

for k=1:4;

x=x0-5*h(k):h(k):x0+5*h(k);

y=cos(2*x.^2-3);

pp=spline(x,y);

dp2=fnder(pp,2);

dy2(k)=vpa(fnval(dp2,x0),9);

err(k)=vpa(abs(dy2(k)-dy),9);

end

[h',dy2',err']

结果为

ans =

[ 1/10, 7.15436471, .14668491]

[ 1/100, 7.00911088, .143108e-2]

[ 1/1000, 7.00769411, .1431e-4]

[ 1/10000, 7.00767990, .10e-6]

实验12（数列的极限）

实验目的

1.加深对极限概念的理解。

2.学会用MATLAB软件计算极限。

3.应用极限解决实际问题。

实验内容

1.用数值计算和图形展示相结合的方法研究数列和函数的极限。

2.用符号演算和数值方法计算数列和函数极限。

3.用数列或函数方法建立简单实际问题的数学模型，并用MATLAB求其极限。

求极限

(1)

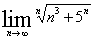
>>syms n

>>limi(t(n^3+5^n)^(1/n),n,inf)

结果为：

ans=

(2)

>>syms n

>>limit((sqrt(n+3)-3*sqrt(n+1)+sqrt(n)),n,inf)

结果为：

ans =

3^(1/2)-3

(3)

>>syms m n

>>limit((cos(m/n))^n,n,inf)

结果为：

ans =

(-1 .. 1)^n

（4）：

>>syms n

>>limit((exp^(1/n)),n,inf)

结果为：

ans =

NaN

（5）：

>>syms x

>>limit((1/x)*sin(1/x),x,inf)

结果为：

ans=

(6)：

>>syms x

>>limit((1/x)/(exp(x)-1),x,inf)

结果为：

ans =

(7)：

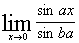>>syms x a b

>>limit(sin(a*x)/sin(b*x)，x,0)

结果为：

ans=

a/b

(8)：

>>syms x

>>limit((1-cos(x))/x*sin(x),x,0)

结果为：

ans =

实验13（函数的导数与最值）

实验目的

1.加深对导数的理解。

2.学会用MATLAB软件计算导数和函数最值。

3.应用最值计算方法解决实际问题。

实验内容

1.用数值计算和图形展示相结合的方法研究函数的导数。

2.用符号演算法和数值方法计算函数的导数和最值。

3.用函数最值方法解决一些简单的实际问题，并用MATLAB求其解。

求函数z=x^4+y^4-4xy+1的极值，并对图形进行观察。

解：

x=0:0.01:1;

y=0:0.01:1;

[X,Y]=meshgrid(x,y);

Z=X.^4+Y.^4-4.*X.*Y+1;

surf(X,Y,Z)

syms x y;

Z=x^4+y^4-4*x*y+1;

Zx=diff(Z,x,1);

Zy=diff(Z,y,1);

simplify(Zx)

simplify(Zy)

结果为

ans =

4*x^3-4*y

ans =

4*y^3-4*x

[x,y]=solve('4*x^3-4*y,4*y^3-4*x','x','y')

结果为

x =

-i

-1

(1/2-1/2*i)*2^(1/2)

(-1/2+1/2*i)*2^(1/2)

(1/2+1/2*i)*2^(1/2)

(-1/2-1/2*i)*2^(1/2)

y =

-i

-1

-1/2*2^(1/2)-1/2*i*2^(1/2)

1/2*2^(1/2)+1/2*i*2^(1/2)

-1/2*2^(1/2)+1/2*i*2^(1/2)

1/2*2^(1/2)-1/2*i*2^(1/2)

实验14（级数与函数逼近）

实验目的

1.学会用MATLAB判别级数的敛散性。

2.加深对函数项级数的认识并了解与此相关的函数逼近知识。

实验内容

1.用数值计算和图形展示相结合的方法研究级数的敛散性。

2.用符号演示法和数值方法计算数项级数的和。

3.函数项级数、幂级数、傅里叶级数。

写出函数y=tanx的幂级数展开式，并利用图形考察幂级数部分和逼近函数的情况。

解：

x0=-pi:0.01:pi;

y0=tan(x0);

syms x;

y=tan(x);

plot(x0,y0,'r--'),axis([-2*pi,2*pi,-2,2]);

hold on

p=taylor(y,x,2),y1=subs(p,x,x0);

line(x0,y1)

xlabel('x轴');ylabel('y轴');

gtext('tan(x)');gtext('2阶泰勒展开式')

p =

x+1/3*x^3

p =

x+1/3*x^3+2/15*x^5+17/315*x^7

相关推荐

数学实验报告

专栏推荐